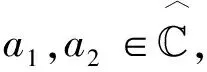p阶零级的亚纯函数的Borel例外值
(中山开放大学,广东 中山,528402)
1 引言与主要结果
定理A如果f(z)是超越的全纯函数,其增长级满足:0<ρ(f)<∞,这里
则对于任意有限复数a,都有
μ(f-a)=ρ(f)
至多有一个a值例外,其中μ(f-a)称为f(z)-a的零点序列的收敛指数,可根据如下定义1给出.
定义1给定复数序列{zn},满足条件:0<|z1|≤|z2|≤… (如果{zn}是无穷序列,则有|zn|→∞(n→∞)).用n(r)表示圆盘Dr={z:|z|≤r}内所含序列{zn}中复数的个数(按重数计算),称之为序列{zn}的计数函数. 令
称其为序列{zn}的收敛指数.
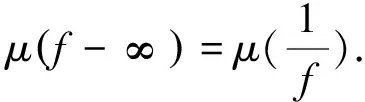
定理A中的例外值称为全纯函数f(z)的Borel值.
1929年,芬兰数学家Nevanlinna发展了一套理论,引进亚纯函数的特征函数T(r,f),将上述结果推广到亚纯函数[3]:
定理B如果f(z)是超越的亚纯函数,其增长级满足:0<ρ(f)<∞,这里
μ(f-a)=ρ(f)
至多有两个a值例外.
定理B中的例外值称为亚纯函数f(z)的Borel值.
此后,众多学者从不同的角度对上述定理进行了推广[4-6].最近,我们对于ρ(f)=∞的情形,采用Sato引进的方法[7],将Borel定理推广到具有p阶正级的亚纯函数的情形,给出了如下定理[8].

μp(f-a)=ρp(f)
至多有两个a值例外.其中
称为f(z)的p阶增长级,这里log[1]u=log+u,log[k+1]u=log+{log[k]u}.而μp(f-a)是f(z)-a的零点序列{zn}的p阶收敛指数,由下列公式定义:
当f(z)是全纯函数时,其p阶增长级还可由下式定义
这里,M(r,f)是f(z)的最大模函数.
我们称上述定理中的例外值为亚纯函数f(z)的p阶Borel值.
这些结果都没有论及增长级ρp(f)=0的情形.有学者断言:ρ(f)=0的亚纯函数没有Borel值!其实不然!我们发现:存在ρ(f)=0的超越亚纯函数,有一个Picard值!当然,更可以有一个Borel值.
本文,我们采用Juneja等学者的方法[10],对满足ρp(f)=0的亚纯函数的增长性进行更细致的刻划,引进如下定义.
定义2给定整数p≥1,设f(z)是p阶零级、p-1阶无穷的超越亚纯函数,即有:ρp(f)=0,ρp-1(f)=∞.对于整数l≥m≥0,称
为f(z)的p阶零级增长型.进一步,
(1) 称f(z)是p阶零级极小型的,如果存在m≥0,使得:1≤σp(m,m+1;f)<∞;
(2) 称f(z)是p阶零级极大型的,如果存在m≥1,使得:0<σp(m,m;f)≤1;
(3)称f(z)是p阶零级中间型的,如果对所有l≥m≥0,有:σp(m,l;f)=0或∞.
当f(z)是全纯函数时,其p阶零级增长型还可由下式定义
相应地,还要对p阶收敛指数为零的复数序列{zn},给出增长型的概念.
定义3给定复数序列{zn},满足条件:μp({zn})=0,μp-1({zn})=∞.对于整数l≥m≥0,称
为{zn}的p阶零级增长型.进一步,
(1) 称{zn}是p阶零级极小型的,如果存在m≥0,使得:1≤λp(m,m+1;{zn})<∞;
(2) 称{zn}是p阶零级极大型的,如果存在m≥1,使得:0<λp(m,m;{zn})≤1;
(3) 称{zn}是p阶零级中间型的,如果对所有n≥m≥0,有:λp(m,n;{zn})=0或∞.
特别地,当{zn}是函数f(z)-a的全部非零零点序列时,{zn}的型称为f(z)的a值点列的型, 记为
λp(m,l;f-a)=λp(m,l;{zn}).
现在,我们可以考虑推广定理B和C到零级的情形,给出如下定理.

μp(f-a)=0,μp-1(f-a)=∞,
且f(z)的a值点列的p阶零级增长型等于f(z)的p阶零级增长型,即对于所有l≥m≥0,有:
λp(m,l;f-a)=σp(m,l;f),
当p>1时,至多有两个a值例外;而当p=1时,至多有一个a值例外.
我们称上述定理中的例外值为函数f(z)的p阶零级Borel值.
特别地,作为定理1的推论,我们有:
推论1如果f(z)是1阶零级的超越全纯函数,则f(z)没有Borel值和Picard值.
2 p阶零级增长型的比较
为了证明我们的结论,需要在亚纯函数的p阶零级增长型之间引进高低比较的概念.
命题1设整数p≥1.如果f(z)是p阶零级、p-1阶无穷的亚纯函数,则对于任意l≥m≥0,σp(m,l;f)具有下列性质:
(1)0≤σp(m,m;f)≤1,m=1,2,…;
(2)σp(l,m;f)=0,1≤m (3)1≤σp(m-1,m;f)≤∞,m=1,2,…; (4)σp(m-1,l;f)=∞,1≤m (5) 如果存在整数k≥1,使得σp(k,k;f)>0,则可记k=inf{k′:0<σp(k′,k′;g)≤1},从而有:1≤m (6) 如果存在整数k≥1,使得σp(k-1,k;f)<∞,则可记k=inf{k′:1≤σp(k′,k′+1;f)<∞},从而有:1≤m 证明由ρp(f)=0可知:对于ε>0,当r充分大时有:log[p]T(r,f)≤εlogr.于是有: log[p+1]T(r,f)≤logε+log[2]r. (2.1) 由此可得:0≤σp(1,1;f)≤1.对上式两端取对数,就可得:0≤σp(2,2;f)≤1.如此下去,就得到性质(1). 从(2.1)式可得:σp(2,1;f)=0,进而易知:σp(n,1;f)=0,n≥2.类似地,从σp(m,m;f)≤1,可导出:σp(l,m;f)=0,l>m.这就是性质(2). 由ρp-1(f)=∞可知:任取实数A>0,存在序列{rn}使得:log[p-1]T(rn,f)≥Alogrn,于是有: log[p]T(rn,f)≥logA+log[2]rn. (2.2) 由此可得:1≤σp(0,1;f)≤∞.对上式两端取对数,就可得:1≤σp(1,2;f)≤∞.如此下去,就得到性质(3). 从(2.2)式还可得σp(0,2;f)=∞,进而知:σp(0,l;f)=∞,l≥2.类似地,从1≤σp(m-1,m;f),可导出:σp(m-1,l;f)=∞,l>m.这就是性质(4). 如果存在整数k≥1,使得σp(k,k;f)>0,记σ=σp(k,k;f),对于ε>0且σ-ε>0,则有序列{rn}使得:log[p+k]T(rn,f)≥(σ-ε)log[k+1]rn,因而可得:σp(k,k+m;f)=∞,m=1,2,….再对上式两边取对数,有:log[p+k+1]T(rn,f)≥log(σ-ε)+log[k+2]rn,结合性质1可得:σp(k+1,k+1;f)=1.重复此步骤,就得:σp(k+m,k+m;f)=1,m=1,2,….由此,可得:σp(k+m,k+m+1;f)=∞,m=1,2,….记k=inf{k′:0<σp(k′,k′;f)≤1},这表明m≥k时有σp(m,m+1;f)=∞.再考虑1≤m 如果存在整数k≥1,使得σp(k-1,k;f)<∞,记σ=σp(k-1,k;f),对于ε>0,则当r充分大时有:log[p+k-1]T(r,f)≤(σ+ε)log[k+1]r.因而得到:log[p+k]T(r,f)≤log(σ+ε)+log[k+2]r.由此得:σp(k,k;f)=0,再结合性质(3)可得:σp(k,k+1;f)=1.重复此步骤,进而可得:σp(k+m-1,k+m;f)=1,m=1,2,….由此可得:σp(k+m,k+m;f)=0,m=1,2,….记k=inf{k′:1≤σp(k′,k′+1;f)<∞}.这表明m≥k时有σp(m,m;f)=0.再考虑1≤m 命题证毕. 作为命题1的推论,我们有如下: 命题2设整数p≥1,f(z)是p阶零级、p-1阶无穷的亚纯函数,则下列结论成立: (1)如果f(z)不是极小型的,则对所有整数m≥0,总有σp(m,m+1;f)=∞. (2)如果f(z)不是极大型的,则对所有整数m≥1,总有σp(m,m;f)=0. (3)如果f(z)既不是极小型的,也不是极大型的,则f(z)必是中间型的. 命题3设整数p≥1.如果f(z)和g(z)都是p阶零级、p-1阶无穷的亚纯函数,则下列结论成立: (1)当f(z)是极小型的,g(z)是中间型的时,存在整数k≥0,使得:σp(k,k+1;f)<σp(k,k+1;g),且对于任意l≥m≥0,皆有σp(m,l;f)≤σp(m,l;g). (2)当f(z)是中间型的,g(z)是极大型的时,存在整数k≥1,使得:σp(k,k;f)<σp(k,k;g),且对于任意l≥m≥0,皆有σp(m,l;f)≤σp(m,l;g). (3)当f(z)是极小型的,g(z)是极大型的时,存在整数k≥0,使得:σp(k,k+1;f)<σp(k,k+1;g);或者,存在整数k′≥1,使得:σp(k′,k′;f)<σp(k′,k′;g);且对于任意l≥m≥0,皆有σp(m,l;f)≤σp(m,l;g). 证明由f(z)是极小型的可知:存在k′≥0,使得:1≤σp(k′,k′+1;f)<∞.不妨记 k=inf{k′:1≤σp(k′,k′+1;f)<∞}, 则有:1≤σp(k,k+1;f)<∞,σp(k+l,k+1;f)=0,σp(k+l,k+l+1;f)=1,l=1,2,…;以及:σp(m,m+1;f)=∞,0≤m 由g(z)是极大型的可知:存在k′≥1,使得:0<σp(k′,k′;g)≤1.不妨记 k=inf{k′:0<σp(k′,k′;g)≤1}, 则有:0<σp(k,k;g)≤1,σp(k+l,k+l;g)=1,σp(k+l,k+l+1;g)=∞,l=1,2,…;以及:σp(m,m;g)=0,1≤m 由f(z)是极小型的可知:存在k≥0,k=inf{k′:1≤σp(k′,k′+1;f)<∞},满足1≤σp(k,k+1;f)<∞.而由g(z)是极大型的可知:存在k′≥1,k′=inf{k:0<σp(k,k;g)≤1},满足0<σp(k′,k′;g)≤1.于是,由性质(5)知:σp(k,k+1;f)<∞=σp(k,k+1;g);或者由性质(6)知:σp(k′,k′;f)=0<σp(k′,k′;g).这就是结论(3). 至此,命题得证. 现在,根据命题3,我们引进如下定义. 定义4给定整数p≥1,设f(z)和g(z)都是p阶零级、p-1阶无穷的亚纯函数,称f(z)的增长型低于g(z)的增长型(或称g(z)的增长型高于f(z)的增长型),如果下列条件之一成立: (1)f(z)是极小型的,g(z)是中间型的; (2)f(z)是极小型的,g(z)是极大型的; (3)f(z)是中间型的,g(z)是极大型的; (4)f(z)和g(z)都是极小型的,k=inf{k′:1≤σp(k′,k′+1;f)<∞},l=inf{k′:1≤σp(k′,k′+1;g)<∞},且k (5)f(z)和g(z)都是极小型的,k=inf{k′:1≤σp(k′,k′+1;f)<∞}=inf{k′:1≤σp(k′,k′+1;g)<∞},且σp(k,k+1;f)<σp(k,k+1;g); (6)f(z)和g(z)都是极大型的,k=inf{k′:0<σp(k′,k′;f)},l=inf{k′:0<σp(k′,k′;g)},且k>l(此时有σp(l,l;f)=0<σp(l,l;g)); (7)f(z)和g(z)都是极大型的,k=inf{k′:0<σp(k′,k′;f)}=inf{k′:0<σp(k′,k′;g)},且σp(k,k;f)<σp(k,k;g). 本节,我们给出几个后面要用到的引理. 引理1给定整数p≥1,设f(z)和g(z)都是p阶零级、p-1阶无穷的亚纯函数,则它们的和、差、积、商都是p阶零级的亚纯函数.进一步,如果f(z)的增长型低于g(z)的增长型,则f(z)+g(z)和f(z)g(z)的增长型都等于g(z)的增长型. 证明由特征函数的性质:T(r,f+g)≤T(r,f)+T(r,g)+log2和T(r,fg)≤T(r,f)+T(r,g),不难得到:ρp(f+g)≤max{ρp(f),ρp(g)}=0和ρp(fg)≤max{ρp(f),ρp(g)}=0.其次,由ρp(g)=ρp(-g),可得ρp(f-g)=0.再由Nevanlinna第一基本定理,可得:ρp(g)=ρp(1/g),因此ρp(f/g)=0.这就完成引理前半部分的证明. 如果f(z)的增长型低于g(z)的增长型,先证明f(z)+g(z)的增长型等于g(z)的增长型.依据定义4和命题3,可分为两种情形: 情形一,存在整数k≥0,使得:σp(k,k+1;f)<σp(k,k+1;g).由特征函数的性质,我们有 σp(k,k+1;f+g)≤max{σp(k,k+1;f),σp(k,k+1;g)}=σp(k,k+1;g), 和σp(k,k+1;f)=σp(k,k+1;-f),再结合g=(f+g)+(-f),便得 σp(k,k+1;g)≤max{σp(k,k+1;f+g),σp(k,k+1;-f)}≤σp(k,k+1;g). 这就导出:σp(k,k+1;f+g)=σp(k,k+1;g).由此我们断言:ρp-1(f+g)=∞,因而f(z)+g(z)的增长型等于g(z)的增长型. 为证明上述断言,假设ρp-1(f+g)<∞,则有σp-1(m,m;f+g)≤1,m=1,2,….这等同于σp(m-1,m;f+g)≤1,m=1,2,….对于m=k+1,就有σp(k,k+1;f+g)=σp(k,k+1;g)≤1.另一方面,由σp(k,k+1;f)<σp(k,k+1;g)和命题1中性质(3)知必有:1<σp(k,k+1;g).矛盾!这表明我们的断言成立. 情形二,存在整数k≥1,使得:σp(k,k;f)<σp(k,k;g).由特征函数的性质,我们有 σp(k,k;f+g)≤max{σp(k,k;f),σp(k,k;g)}=σp(k,k;g) 和σp(k,k;f)=σp(k,k;-f),再结合g=(f+g)+(-f),便得 σp(k,k;g)≤max{σp(k,k;f+g),σp(k,k;-f)}≤σp(k,k;g). 这就导出:σp(k,k;f+g)=σp(k,k;g).由此,我们断言:ρp-1(f+g)=∞,因而f(z)+g(z)的增长型等于g(z)的增长型. 为证明上述断言,假设ρp-1(f+g)<∞,则有σp-1(m,m;f+g)≤1,m=1,2,….这等同于σp(m-1,m;f+g)≤1,m=1,2,….对于m=k,就有σp(k-1,k;f+g)=σp(k-1,k;g)≤1.另一方面,由σp(k,k;f)<σp(k,k;g)和命题1中性质(5)知必有:σp(k-1,k;g)=∞.矛盾!这表明我们的断言成立. 完全类似地讨论,可证明f(z)g(z)的增长型也等于g(z)的增长型. 引理得证. λp(m,l;{zn})≤σp(m,l;f). (3.1) (3.2) 由此可得: μp(f-a)≤ρp(f)=0, 即f(z)-a的零点序列{zn}也是p阶零级的.进一步,当{zn}是p-1阶无穷的时,由定义3和定义2,结合(3.2)式,不难得到(3.1)式. 引理得证. 引理3给定整数p≥1,设φ(z)是p阶零级、p-1阶无穷的全纯函数,则f(z)=exp(φ(z))是p+1阶零级、p阶无穷的全纯函数. 证明由ρp(φ)=0,及M(r,f)≤exp(M(r,φ)),可得ρp+1(f)=0.其次,由ρp-1(φ)=∞,存在序列{rn},使得 应用Pòlya关于复合函数最大模的一个不等式[11]: 其中0 因而可得: 此即:ρp(f)=∞.故引理得证. 特别地,当φ(z)为超越全纯函数时,我们有[12]: 即φ(z)是零阶无穷的全纯函数,因而依据上述引理结论,f(z)=exp(φ(z))是1阶无穷的全纯函数,即有:ρ1(f)=∞. 引理4给定实数区间(0,∞)上的非降正值函数α(x)和β(x),满足条件: 则对所有整数m≥1,都成立: 这里exp[1](u)=eu,exp[m+1](u)=exp {exp[m](u)}. 证明我们对m用数学归纳法来证明引理结论. 先考虑m=1的情形.由 及 可得 即m=1的时候,引理结论成立. 假设m=k的时候引理结论也成立.再考虑m=k+1的情形. 记α1(x)=exp{α(x)},β1(x)=exp{β(x)},则α1(x)和β1(x)也满足引理条件.根据归纳假设,可得: 于是由归纳法可知引理结论成立. 引理得证. 引理5给定整数p≥1,若复数序列{zn}是p阶零级、p-1阶无穷的,即满足条件:μp({zn})=0,μp-1({zn})=∞,则{zn}的p阶零级增长型还可由下式给出: 这里整数l≥m≥0. 证明记rn=|zn|,n(r)是序列{zn}的计数函数,由n(rn)≥n,可得: 另一方面,{rn}中必存在一个子序列{rnk}(k=1,2,…)满足条件:rnk→∞(k→∞)以及 rnk 则当rnk≤r 引理得证. 引理6给定整数p≥1,如果f(z)是p阶零级、p-1阶无穷的超越全纯函数,具有幂级数展式 其中ak皆不为零,则f(z)的p阶零级增长型满足: 证明记 先考虑σ<∞的情形,则对于ε>0,当r>r0=r0(ε)时,有 logM(r,f) 由关于幂级数系数的Cauchy不等式,可从上式导出:对所有k≥1,成立 log|ak| 取 可得: 于是,当k充分大时,有: 由此可归纳地导出: 进而可得: 再令ε→0,便得到: 对于σ=∞的情形,上式显然成立. 为证相反的不等式,记 同样先考虑σ<∞的情形,则对于ε>0,当k>k0=k0(ε)时,有 而由 其中A(k0)是次数不高于k0的多项式,S是一个整数满足条件:S M(r,f) 注意到上式中两个级数都是收敛的,可以得到: log[2]M(r,f) 因此有: 再令ε→0,便得到: 对于σ=∞的情形,上式显然成立. 故此引理得证. 引理7设整数p≥1,f(z)是p阶零级、p-1阶无穷的亚纯函数,则其导数f′(z)也是p阶零级、p-1阶无穷的亚纯函数,且f′(z)的p阶零级增长型等于f(z)的p阶零级增长型. 证明由[13] T(r,f)<Ο(T(2r,f′)+logr) 和[14] T(r,f′)<2T(r,f)+S(r,f) 易得证引理结论. 给定复数序列{zn},满足条件:0<|z1|≤|z2|≤… ,|zn|→∞(n→∞).Weierstrass最早认识到[12]:可以适当地选取正整数序列{λn},使得无穷乘积 (4.1) 是复数平面上的全纯函数.Borel发现[1]:当μ1({zn})<∞时,可以取整数λn=q,n=1,2,…,满足q≤μ1({zn})≤q+1,使得μ1({zn})=ρ1(Φ).我们最近发现[8]:对于p≥1,当μp({zn})<∞时,可以取λn=[logn],n=1,2,…,这里[u]是u的整数部分,使得μp({zn})=ρp(Φ).我们称这样的Φ(z)为序列{zn}形成的典型乘积. 本节,我们在文[8]的基础上,给出更进一步的结论: 定理2设整数p≥1.如果复数序列{zn}是p阶零级、p-1阶无穷的,则它形成的典型乘积Φ(z)是p阶零级、p-1阶无穷的全纯函数,且Φ(z)的增长型等于序列{zn}的增长型. 证明依据文[9],我们仅须证明Φ(z)的增长型等于序列{zn}的增长型.依据引理2可得到: 对p≥1和任意整数l≥m≥0,皆有 λp(m,l;{zn})≤σp(m,l;Φ). 为证明相反的不等式,记λp(m,l;{zn})=λ,先考虑λ<∞的情形.对于ε>0,当r>r0=r0(ε)时,有 n(r) (4.2) 另外,记rn=|zn|,考虑级数 (4.3) 其中,nk是整数满足条件:[lognk]=k和[log(nk-1)]=k-1,这里[u]表示u的整数部分.特别地,记n0=1,容易计算出:n1=3,n2=8,n3=21,n4=55,等等.且不难证明[8]: (4.4) 由(4.3)式,有ak皆不为零,且 据此,结合(4.4)式,可对l≥1归纳地得出:当k充分大时,成立 另一方面,我们有log[p+m-1]k≤log2+log[p+m-1](k-1),则有 注意到log[p+m-1](k-1)≤log[p+m]nk-1,再结合引理6和引理5,可得: 于是对于上述ε>0,当r>r1=r1(ε)时,有 M(r,h) (4.5) 现在,我们来估计log|Φ(z)|,固定|z|=r,记(4.1)中通项为 (4.6) 结合(4.2)式有 ≤(logn(r)+1)M(r,h)<2exp[p+m-2]((log[l]r)λ+ε)×exp[p+m-1]((log[l]r)λ+ε). (4.7) <2exp[p+m-2]((log[l]2r)λ+ε)×exp[p+m-1]((log[l]2r)λ+ε). (4.8) 则有 (4.9) 将(4.7),(4.8)和(4.9)代入(4.6)式中,可以得到: log[2]M(r,Φ)≤5exp[p+m-2]((log[l]2r)λ+ε)+log4, 从而有 令ε→∞,就得到: σp(m,l;Φ)≤λp(m,l;{zn}). 当λ=∞时,上式显然成立. 定理得证. 在亚纯函数值分布的研究中,Nevanlinna发展的特征函数法有着非常重要的作用,开拓了崭新的研究领域,收获了丰富多彩的成果.这一方法的巨大成功,使得人们逐渐淡忘了早期Borel获得关于全纯函数的Borel定理时所用的因子分解法. 其实,因子分解法是一个偏重于构造性的方法.而要证明我们的结果,使用因子分解法或许更恰当些.此外,我们还需要用到Borel关于全纯函数组的一个定理,借助它才可以不使用Nevanlinna第二基本定理,直接将Borel关于全纯函数的例外值定理推广到亚纯函数[8].因此,为证明定理1,我们需要如下结论: 定理3给定整数p>1,设fj(z),φj(z),j=1,2,…,n是两组全纯函数,满足条件: (1)f1(z)exp(φ1(z))+f2(z)exp(φ2(z))+…+fn(z)exp(φn(z))=0; (2)fj(z)都是p阶零级的,φj(z)都是p-1阶零级、p-2阶无穷的,j=1,2,…,n; (3)当1≤j≤n,1≤h,k≤n,h≠k时,fj(z)的p阶零级增长型低于exp (φh(z)-φk(z))的p阶零级增长型. 则有:fj(z)≡0,j=1,2,…,n. 证明我们对于n(>1)使用归纳法. 先考虑n=2的情形.假设定理结论不真,则不妨设f1(z)≢0. 于是根据条件(1),可有: 而由条件(2),上式右端亚纯函数的p阶零级增长型低于左端函数的p阶零级增长型,矛盾!这一矛盾说明假设是不对的,因而定理结论成立. 现假设n=m时定理结论成立,再考虑n=m+1的情形.由条件(1),有: f1(z)exp(φ1(z))+…+fm(z)exp(φm(z))+fm+1(z)exp(φm+1(z))=0. (5.1) 如果fm+1(z)≡0,则由归纳假设可得:fj(z)≡0,j=1,2,…,m.故可设fm+1(z)≢0,并令 (5.2) 则可将(5.1)式改写为: g1(z)exp(ψ1(z))+g2(z)exp(ψ2(z))+…+gm(z)exp(ψm(z))=1, (5.3) 根据引理1和(5.2)式,这里的gj(z),exp(ψj(z)),j=1,2,…,m,也满足条件(2)和(3). 对(5.3)式两端求导数,得到: (g′1+ψ′1g1)exp(ψ1(z))+…+(g′m+ψ′mgm)exp(ψm(z))=0. (5.4) 由引理1和引理7知g′j+ψ′jgj的p阶零级增长型不高于gj(z)的p阶零级增长型,从而知g′j+ψ′jgj,exp(ψj(z)),j=1,2,…,m,也满足条件(2)和(3).根据归纳假设和(5.4)式,可得: g′j+ψ′jgj≡0,j=1,2,…,m. 解微分方程,有: gj(z)=cjexp(-ψj(z)),j=1,2,…,m. 如果cj≠0,则由(5.2)式知:上式左端函数的p阶零级增长型低于右端函数的p阶零级增长型,矛盾!因此,只能有:cj=0.进而有:gj(z)≡0,j=1,2,…,m.将它们代入到(5.1)式中,得到:fm+1(z)≡0,与我们假设fm+1(z)≢0矛盾!因此表明:n=m+1时定理结论也成立. 得证定理. 用完全类似的讨论,我们还可以得到如下结论. 定理4给定整数p≥1,设fj(z),φj(z),j=1,2,…,n;是两组全纯函数,满足条件: (1)f1(z)exp(φ1(z))+f2(z)exp(φ2(z))+…+fn(z)exp(φn(z))=0; (2)fj(z)都是p阶有穷的,j=1,2,…,n; (3)当1≤h,k≤n,h≠k时,exp(φh(z)-φk(z))都是p阶无穷的. 则有:fj(z)≡0,j=1,2,…,n. 这个定理也是文[8]中定理6的推论. 本节,我们借助于定理2,将Hadamard关于全纯函数的因子分解定理推广到p阶零级的亚纯函数的情形.给出如下定理. 定理5给定整数p≥1,如果f(z)是p阶零级、p-1阶无穷的亚纯函数,则它可表示为: (6.1) 且成立下列结论: (1)Ρ1(z)=zmΦ1(z),m≥0是f(z)在原点处的零点的阶数,当f(z)的非零零点序列{zn}是无穷的时,Φ1(z)是f(z)的非零零点序列形成的如(4.1)式所示的典型乘积,而当f(z)的非零零点序列{zn}是有穷的时,Φ1(z)具有形式: (2)Ρ2(z)=zkΦ2(z),k≥0是f(z)在原点处的极点的阶数,当f(z)的非零极点序列{yn}是无穷的时,Φ2(z)是f(z)的非零极点序列形成的如(4.1)式所示的典型乘积,而当f(z)的非零极点序列{yn}是有穷的时,Φ2(z)具有形式: (3)Ρj(z),j=1,2都是p阶零级的全纯函数,且如果Ρj(z)是p-1阶无穷的全纯函数,则Ρj(z)的增长型不高于f(z)的增长型. (4)φ(z)是p-1阶零级的全纯函数,特别地,当p=1时,φ(z)≡c是常数. 证明结论(1)和(2)是显然的.仅需注意到:m>0时,必有k=0;以及k>0时,必有m=0. 根据引理2和定理2便可得到结论(3). 为证结论(4),令 则F(z)是没有零点和极点的亚纯函数,因而有F(z)=eφ(z),这就得到(6.1)式.再依据引理1,可知F(z)是p阶零级的全纯函数.再次应用Pòlya关于复合函数最大模的一个不等式[11]: 其中0 因而可得: ρp-1(φ)≤ρp(F)=0, 即φ(z)是p-1阶零级的全纯函数. 当p=1时,φ(z)是0阶零级的全纯函数,因而有φ(z)≡c是常数. 定理证毕. 情形一,ρp-1(Ρj)<∞,j=1,2,3.先考虑三个复数中一个为零,一个为无穷的场合.不妨设为:a1=0,a2=∞,于是a3≠0,∞,应用定理5,有: (7.1) 且ρp-1(eφ1)=ρp-1(f)=∞. 考虑函数 它是没有零点和极点的亚纯函数,因而有F(z)=eφ2(z),且ρp-1(eφ2)=ρp-1(f)=∞.于是得: Ρ1(z)eφ1(z)-a3Ρ2(z)=Ρ3(z)eφ2(z), (7.2) Ρ1(z)-a3Ρ2(z)e-φ1(z)=Ρ3(z)eφ2(z)-φ1(z). (7.3) 从(7.3)式可得:ρp-1(eφ2-φ1)=ρp-1(e-φ1)=∞.应用定理4,导出:Ρ1(z)≡0,Ρ2(z)≡0,Ρ3(z)≡0.矛盾!这个矛盾说明假设是错误的,即ρp-1(Ρj)<∞,j=1,2,3不能成立. 再考虑三个复数中一个为无穷,没有复数为零的场合.不妨设a2=∞,令g(z)=f(z)-a1,知g(z)是p阶零级、p-1阶无穷的亚纯函数,且记b1=0,b2=∞,b3=a3-a1,则g(z)-bj的全部零点形成的典型乘积就是f(z)-aj的全部零点形成的典型乘积Ρj(z).重复上面的讨论,导出矛盾!故此这种场合也不成立. 因此,情形一不成立. 情形二,存在某个ρp-1(Ρj)=∞.注意到ρp-1(Ρj)<∞时有σp(0,1;Ρj)=σp-1(1,1;Ρj)≤1,即Ρj的p阶零级增长型不高于极小型,从而所有Ρj(z)的p阶零级增长型都低于f(z)的p阶零级增长型,j=1,2,3. 类似于情形一的讨论,应用定理5和定理3可以导出矛盾!故情形二也不成立.这样就证明了定理1对于整数p>1的结论. 先考虑两个复数中一个为零,一个为无穷的场合.不妨设为:a1=0,a2=∞,于是应用定理5,有: (7.4) 这里C为常数.注意到ρ0(Ρj)<∞等价于Ρj(z)是多项式,可知至少有一个ρ0(Ρj)=∞,不妨设为ρ0(Ρ1)=∞.于是由ρ0(Ρ2)<∞时有σ1(0,1;Ρ2)=σ0(1,1;Ρ2)≤1≤σ1(0,1;Ρ1),可知Ρ2(z)的1阶零级增长型不高于Ρ1(z)的1阶零级增长型,从而Ρ1(z)和Ρ2(z)的1阶零级增长型都低于f(z)的1阶零级增长型.对于ρ0(Ρ1)=ρ0(Ρ2)=∞的情形,假设定理结论不真导出Ρ1(z)和Ρ2(z)的1阶零级增长型都低于f(z)的1阶零级增长型. 这样,应用引理1可知,(7.4)式右端函数的1阶零级增长型低于左端函数f(z)的1阶零级增长型.矛盾!这个矛盾说明对于这种场合假设是错误的. 再考虑两个复数中一个为无穷的场合.不妨设为:a2=∞,令g(z)=f(z)-a1,知g(z)是1阶零级、0阶无穷的亚纯函数,且记b1=0,b2=∞,则g(z)-bj的全部零点形成的典型乘积就是f(z)-aj的全部零点形成的典型乘积Ρj(z).重复上面的讨论,导出矛盾!这个矛盾说明对于这种场合假设也是错误的. 于是定理1得证. 现在,我们来给出一些p阶零级的亚纯函数的例子. 例1给定整数p≥1,m≥0,取复数序列{zn}满足条件: 则应用引理4和引理5,可得: μp({zn})=0,μp-1({zn})=∞,λp(m,m+1;{zn})=λ. 应用定理2,可知序列{zn}形成的如(4.1)式所示的典型乘积Φ(z)是p阶零级、p-1阶无穷的极小型的全纯函数. 例2给定整数p≥1,m≥1,取复数序列{zn}满足条件: 则应用引理4和引理5,可得: μp({zn})=0,μp-1({zn})=∞,λp(m,m;{zn})=λ. 应用定理2,可知序列{zn}形成的如(4.1)式所示的典型乘积Φ(z)是p阶零级、p-1阶无穷的极大型的全纯函数. 问题:应该如何构造p阶零级、p-1阶无穷的中间型的全纯函数Φ(z)? 例3给定整数p≥1,取φ(z)是p阶零级、p-1阶无穷的全纯函数,{zn}和{yn}是p阶有穷的复数序列,它们所形成的典型乘积为Φ1(z)和Φ2(z),则Φ1(z)和Φ2(z)都是p阶有穷的全纯函数.令 则f(z)是p+1阶零级、p阶无穷的亚纯函数,以0和∞为其p+1阶零级Borel值. 例4取Φ1(z)为1阶零级的超越全纯函数,Φ2(z)为多项式,令 则f(z)是1阶零级、0阶无穷的亚纯函数,以∞为其1阶零级Borel值,事实上,∞为其Picard值.3 几个引理
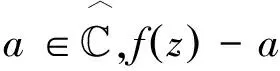
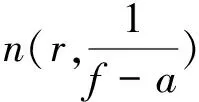
4 p阶零级复数序列形成的典型乘积
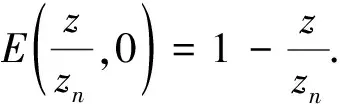



5 p阶零级的全纯函数组的Borel定理
6 p阶零级的亚纯函数的Hadamard因子分解定理
7 定理1的证明