岭回归和核主成分回归在消除共线性中的实证分析及比较

(1. 海南大学理学院，海口，570228;2. 广东财经大学 统计与数学学院，广州，510320)

1 引言

在多元回归分析的过程中，常常会遇到多重共线性的问题.当自变量之间存在严重的多重共线性时，使用最小二乘法得到的回归模型的有效性就会大大降低，模型稳定性也会变得很差，同时给回归系数的统计检验及回归系数的物理含义解释等造成一定的困难.因此采取适当方法消除多重共线性带来的不良影响，对回归模型有着重大意义.国内外学者对消除多重共线性问题得出了许多有效的解决方法，如逐步回归、岭回归、主成分回归、偏最小二乘回归、核主成分回归等.肖雪梦[1]、张应应实例比较了逐步回归、主成分回归及偏最小二乘回归在消除多重共线性中的效果，周鑫[2]实例比较了岭回归和偏最小二乘回归，丁立[3]、钱强强等人实证比较了主成分回归、偏最小二乘回归、岭回归及Lasso法.本文对岭回归和核主成分回归两种方法分别在消除多重共线性的效果上作实例比较分析.

1.1 多重共线性的成因、可能影响及诊断方法

对于多元线性回归模型yi=β0+β1x1i+β2x2i+…+βpxpi+εi(i=1,2,…,n)，回归模型可写作矩阵形式Y=Xβ+ε.当模型违背自变量相互独立的假设，即多个自变量之间存在相互关系时，就会产生多重共线性的问题.多重共线性的主要来源[9]有过度定义回归模型,数据收集的方法有问题,对模型施加了不必要的约束,错误定义回归模型等.

多重共线性的出现会导致每个解释变量的贡献混淆，使得难以解释模型[7],多重共线性的存在会导致均方误差极高,预测变量的方差、协方差和系数变得不合理，使得参数难以精确估计[8].普通最小二乘估计对数据微小变化十分敏感，缺乏稳健性[19].

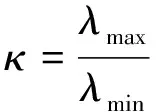
1.2 多重共线性的处理方法

1.2.1 岭回归

岭估计的方法是1970年由Hoerl和Kennard提出的[5]，是对最小二乘估计的一种改进.岭回归实际上就是采用岭估计对回归方程的系数进行估计的过程.当自变量间存在多重共线性时，|X′X|≈0，设想给X′X加上一个正常数矩阵kI(k>0)，那么X′X+kI的奇异程度就会远远小于X′X的奇异程度[4].

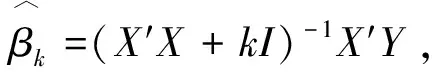
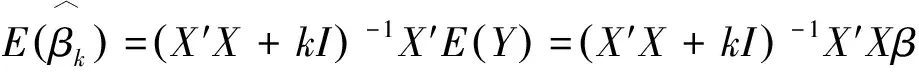
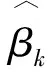
1.2.2 核主成分回归

核主成分回归是将核方法与主成分回归结合起来的一种回归模型，核方法具有良好的性质，可以有效处理高维数据，同时保证较快的计算速度.

核函数理论

定义1设二元函数K:X×X→R，如果存在某个内积空间，以及映射φ:X→H，使得

K(x,y)=[φ(x),φ(y)]，

则称H为特征空间，φ为特征映射，K为核函数[10].

定义2函数K(x,y)称为半正定核函数[11]，如果满足如下条件：

1)函数K(x,y)∈L(X×Y)连续对称；

2)f∈L2(X)；

Mercer定理在特征空间中，对于任意的函数K(x,y)可以表成内积形式

K(x,y)=[φ(x),φ(y)]

的充要条件是K(x,y)是正定的.

常用的Mercer核函数有

1)高斯径向基核函数：

其中σ>0是自定义参数.

2)多项式核函数：

K(x,y)=(x·y+c)σ，

其中c>0，σ是整数，它们是自定义参数.

3)多层感知机核函数：

K(x,y)=tanh(-b(x·y)-c)，

其中b，c是自定义参数.

核主成分回归的基本原理[12]是，先引入非线性变换函数φ:R→F，将原始输入空间映射到某个高维特征空间F，即将输入空间样本点X1,X2,…,Xn变换为特征空间的样本点φ(X1),φ(X2),…,φ(Xn)，再在特征空间F中进行主成分回归.

φ(Xi),φ(Xj)两个F空间样本点的距离用其内积表示，定义核函数为K(Xi,Xj)=(φ(Xi),φ(Xj))，核矩阵为K=[K(Xi,Xj)]n×n.

特征空间中样本点的协方差矩阵为

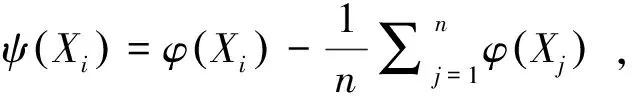
设C的特征值为λ，特征向量为υ，则Cυ=λυ.可以推得

υ=∑ni=1aiψ(Xi),

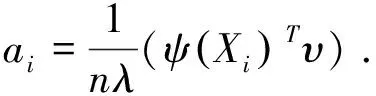
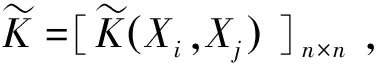
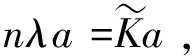
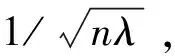
最后对提取出的核主成分建立多元线性回归模型

y=Bω+ε,

其中B=ΨVp，Ψ=(ψ(X1),…,ψ(Xn))，Vp为前p个特征向量组成的矩阵.

运用最小二乘法可求得回归系数为

从而可得核主成分回归模型的方程表示为：

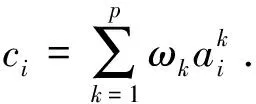
2 实证分析及比较

2.1 数据来源

为了研究我国民航客运量的变化趋势及其成因，我们以民航客运量作为因变量，以国民收入、消费额、铁路客运量、民航航线里程、来华旅游入境人数作为影响民航客运量的主要因素.y表示民航客运量(万人)，x1表示国民收入(亿元)，x2表示消费额(亿元)、x3表示铁路客运量(万人)、x4表示民航航线里程(万公里)、x5表示来华旅游入境人数(万人)，详细数据见[4].

2.2 共线性诊断

首先对原始数据进行标准化处理，将通过标准化的因变量y*对标准化自变量xi*(i=1,2,…,5)进行多元线性回归，并进行多重共线性诊断，通过计算处理得到分析结果如下表1、表2.

表1 共线性统计量

表2 共线性诊断

由表1、表2可知，自变量x1*，x2*的方差膨胀因子都大于10，5维以上的条件数大于10，可见诊断结果一致,表明此回归模型存在较强的共线性.

2.3 岭回归方法

通过计算处理，可得不同岭参数下的回归方程及相应的岭迹图，结果如下表3、图1所示.

表3 不同岭参数下的岭回归(部分)

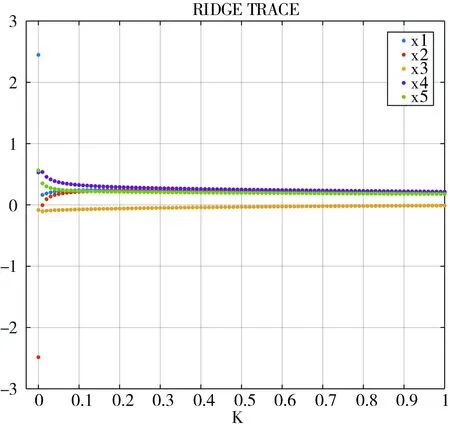
图1 岭迹图

观察岭迹图，可以看出当k≥0.10时，岭回归系数基本趋于稳定，因此选取岭参数k=0.10.此时岭回归方程为

y*=0.2395x1*+0.2141x2*-0.07341x3*+0.3244x4*+0.2278x5*.

方差分析结果及共线性诊断结果如下表4、表5、表6所示.

表4 方差分析表

表5 共线性统计量

表6 共线性诊断

由此可见，岭回归各系数的方差膨胀因子都小于10，各个维度的条件数也都小于10，岭回归能够很好地解决多重共线性问题.

2.4 核主成分回归方法

表7 KPCA特征值和累积贡献

前两个核主成分的累积贡献就已达到95%以上，因此提取KF1，KF2作为回归自变量即可，KF1，KF2如下表8所示.

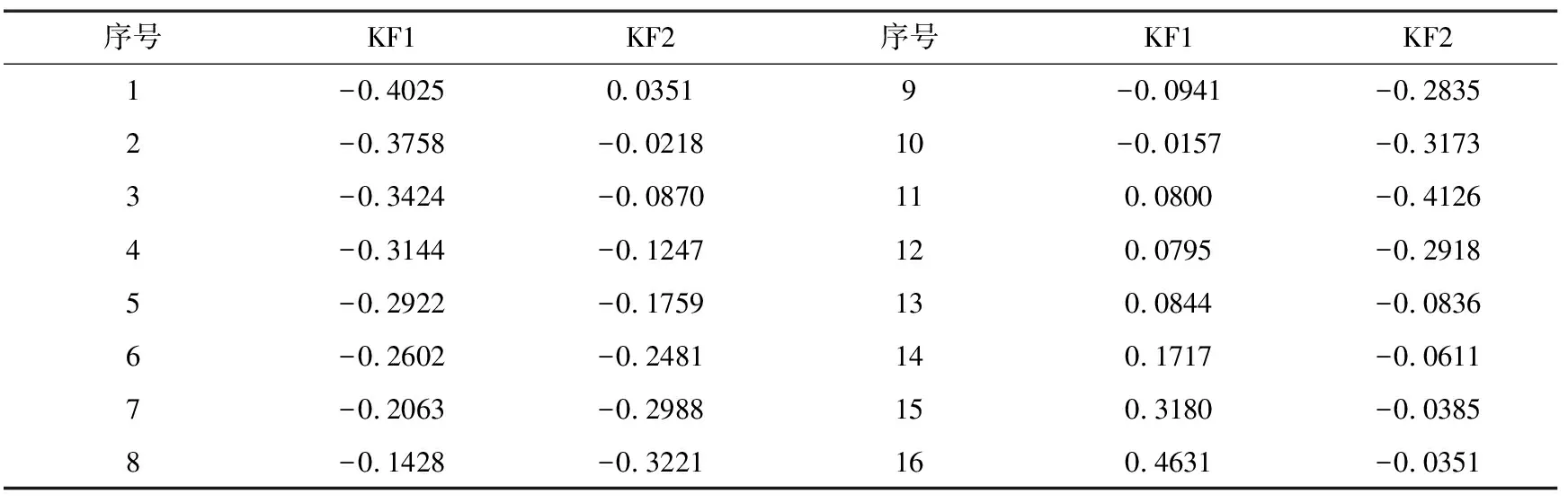
表8 核主成分KF1，KF2

将y*对提取的核主成分KF1，KF2进行多元线性回归，通过计算得到回归方程

y*=0.535+3.754*KF1+1.401*KF2.

方差分析结果及共线性诊断结果如下表9、表10、表11所示.

表9 方差分析表

表10 共线性统计量

表11 共线性诊断

由此可见，回归系数的方差膨胀因子都小于10，各个维度的条件数也都小于10，采用核主成分回归也能消除线性回归过程中的多重共线性问题.

2.5 回归结果对比

岭回归和核主成分回归都能很好地消除多重共线性，对两种方法得到的回归模型结果作比较，结果如下表12所示.

表12 回归结果对比表

由表12可以看出，虽然岭回归在决定系数上略优于核主成分回归，但是在其他指标上均劣于核主成分回归，总的来说，核主成分的回归结果要好于岭回归.

3 总结

本文通过对同一组数据分别用岭回归、核主成分回归的方法进行回归分析，以消除自变量间的多重共线性，并对回归模型结果进行了比较.我们发现这两种回归方法均能有效地消除自变量间的多重共线性，使得回归模型变得更有实际意义，总的来说核主成分回归对内拟合效果要优于岭回归.但是岭回归的岭参数选择，核主成分回归的核函数及核参数的选择都存在很强的主观性，不同的参数选择对回归模型的好坏影响巨大，在实际的问题求解中需要根据专业性及经验性的判断来妥善选择.