诊断复共线性的特征分析法及其在GEO定轨中的应用

韩松辉，杜 兰，归庆明，顾勇为，马朝忠

1.信息工程大学 地理空间信息学院，河南 郑州450052；2.信息工程大学 导航与空天目标工程学院，河南 郑州450052；3.信息工程大学 理学院，河南 郑州450001

1 引 言

复共线性存在于很多测量数据处理问题中，它对估计结果有很大的影响。如果设计矩阵存在复共线性，很小的观测误差就有可能造成估计结果严重偏离真值。为了得到精确、可靠的平差结果，必须消弱和克服设计矩阵复共线性对参数估计的不良影响［1］。

克服复共线性影响的前提是准确地找到设计阵中存在的复共线性关系，即进行复共线性诊断。到目前为止，国内外学者关于复共线性诊断已经提出了10余种方法［1－7］，大致分为3大类：第1类是基于相关系数的方法，第2类是基于特征系统（特征值和特征向量）的方法；第3类是基于条件指标方差分解比的方法。这些方法可以诊断复共线性关系的存在性和严重程度，但在确定复共线性关系的个数时往往存在一些问题，尤其是大部分方法不能准确地确定每个复共线性关系存在于哪些数据列之间，而这些信息对于如何更有针对性地削弱和克服设计阵复共线性对参数估计的不良影响具有重要的参考价值。第3类方法以条件数大小判断是否存在复共线性。该指标是不尽合理的，另外当设计阵存在多个复共线性时，“回归”方法无法全面判断设计阵的复共线性。在上述复共线性诊断方法中，特征分析法简单易行，是一个不错的复共线性诊断方法。特征分析法虽然可以判断设计阵中存在几个复共线性关系，但是法矩阵的特征值比较小是一个很模糊的说法，现实中不易操作。本文对特征分析法进行改进，给出判断小特征值的具体标准。

条件数是目前用来判断复共线性的另一个主要指标。文献［8］专门讨论了广义岭估计的精度随条件数变化的情况。文献［9］利用广义条件数研究了非线性病态法方程的求解问题。随着测量手段的改进，尤其是卫星导航的发展，出现了条件数很大但是LS估计精度很好的测量平差和数据处理情况。条件数大时设计矩阵是否一定存在复共线性，条件数大对LS估计的影响如何都是尚未解决问题。本文用矩阵理论证明了复共线性存在时一定导致条件数很大，反之则不然的结论。然后，讨论条件数大对LS估计的影响。

目前，大多数文献在发现病态性后，直接采用正则化方法或有偏估计等方法来克服病态性对估计值的危害［10－11］，而没有事先对复共线性进行详实的全面诊断、进而有效地利用病态性信息构造更有针对性的正则化方法或有偏估计以更好地消除病态性的影响。文献［7］利用LS估计的信噪比揭示了复共线性结构的特征，然后提出基于信噪比的正则化方法，对设计阵的复共线性作出了比较准确的、有节制的消除。本文则利用改进的特征分析法诊断出设计阵的具体复共线性关系后将提出更有针对性的双k型岭估计。

在GEO定轨数据处理中，由于卫星的高轨静地特性和受限的地面区域跟踪，定轨动力学约束弱且观测几何结构差，引起法方程的病态性［12－13］。在仿真算例中，本文运用上述方法对GEO定轨数据处理中的病态性问题进行分析讨论。诊断出GEO定轨数据处理中法矩阵的复共线性个数和各复共线性具体存在于哪几列之间，并用基于复共线性诊断提出的双k型岭估计克服复共线性的影响。

2 改进的特征分析法

设线性模型为

式中，L为观测值向量；A为设计阵；X为未知参数向量；Δ为观测误差向量，假设E（Δ）＝0，cov（Δ）＝σ20P－1，σ0为未知的单位权中误差，权阵P为已知对称正定阵。线性模型的法矩阵为N＝ATPA，设λ1≤λ2≤…≤λt为N的特征值，Q＝［q1q2…qt］为对应的正则化特征向量构成的正交矩阵。

2.1 复共线性关系存在性诊断

目前，当法矩阵存在小的特征值时，表明法矩阵存在复共线性已经得到许多学者的认可［1，14］。但是什么是小的特征值是一个很模糊的说法。实际上，不可单纯地从特征值本身的大小判断是否存在复共线性，而是应该从特征值对法矩阵各列之间关系的影响大小判断法矩阵是否存在复共线性。

法矩阵特征值求解表达式为

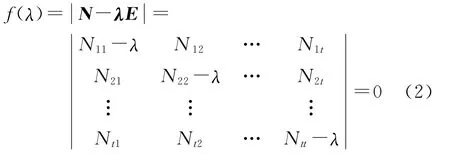
式中，当特征值λ相对于法矩阵元素绝对值很小时，则λ的存在对法矩阵对角线上的t个元素N11、N22、…、Ntt的改变很小，即λ的存在对法矩阵各列之间的关系影响很小。由于f（λ）是关于λ的连续函数，故当λ很小时，可得

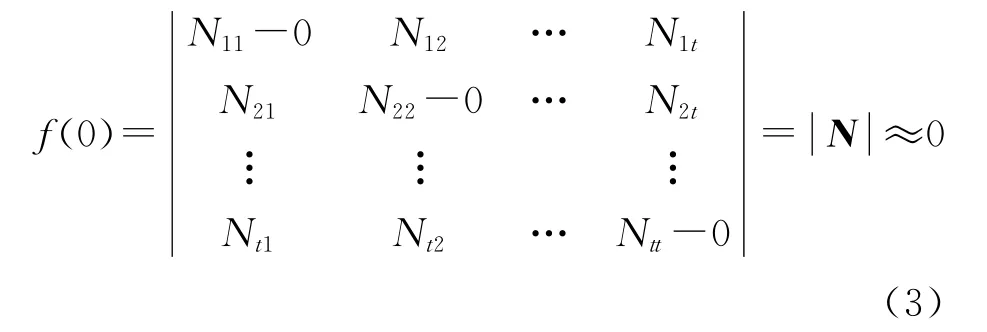
式中，说明法矩阵各列之间近似线性相关，即法矩阵存在复共线性关系。如果λ本身比较大，只是λ相对于法矩阵中元素绝对值很小，则λ和法矩阵所有元素同除以一个常数，总能把λ变成一个比较小的数，使得表达式（3）成立。

如果不存在相对于法矩阵中元素绝对值很小的特征值，则表达式（3）不成立。此时最小特征值λ1相对于也不小，所以λ1的存在已经改变了法矩阵中各列之间的线性关系，即法矩阵各列之间的线性关系经过大的改变之后才使得f（λ1）＝0成立。另外，此处的λ1是最小的特征值，其他特征值令f（λ）＝0成立时对法矩阵各列之间的线性关系改变更大。故此时法矩阵的各列之间本身不存在近似的线性关系，即法矩阵不存在复共线性关系。

综上可知，判断法矩阵是否存在复共线性，不能简单地看特征值本身大小，应看特征值相对于法矩阵元素绝对值的大小。如果法矩阵存在相对于其自身元素绝对值很小的特征值，则说明法矩阵或是设计矩阵存在复共线性关系。一般特征值的数量级小于法矩阵元素绝对值最小值10－2以上的才能算是小的特征值。

2.2 具体复共线性关系诊断

根据特征分析法，设计阵存在复共线性与小的特征值是对应的。首先考虑最小的特征值λ1，由λ1可得

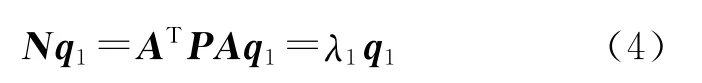
由于λ1对应一个复共线性，复共线性关系是近似的线性关系，故

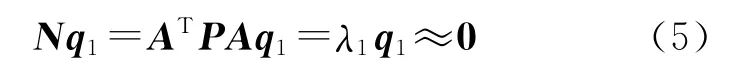
由于法矩阵N和设计矩阵A具有相同的复共线性，所以可得

设A＝［a1a2…at］，q1＝［q11q21…qt1］T，有

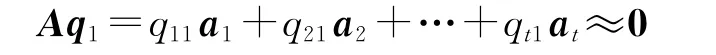
式中，Aq1是由t个列qi1ai（i＝1，2，…，t）相加得到的近似等于0的向量。此处Aq1近似等于0是由于设计矩阵中存在一个复共线性引起的，因此设计矩阵中有几列元素之间存在近似的线性关系。故矩阵［q11a1q21a2…qt1at］的t个列中会出现几列元素绝对值大于其余列元素绝对值的现象，这几列即是对此复共线性贡献比较大的几列。记设计阵中r个列qi11ai1、qi21ai2、…、qir1air（r≤t）的元素绝对值比较大，删除其余的列不影响表达式Aq1≈0的成立，故可得

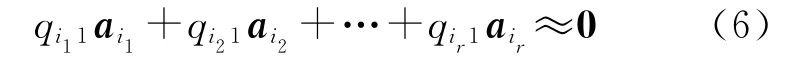
式中，设计矩阵A中r个列ai1、ai2、…、air之间存在复共线性关系，而这个复共线性关系的系数即为q1中的元素qi11、qi21、…、qir1。

3 复共线性与条件数的关系

除了特征分析法外，条件数也是目前常用的判断复共线性的指标。在很多情况下条件数大就表明法矩阵存在病态性。但是随着测量手段的改进，尤其是卫星导航的发展，出现了条件数很大但是LS估计精度很好的测量平差和数据处理情况。由此引发条件数和复共线性之间的严格关系是什么的思考。

3.1 存在复共线性时条件数一定大

对于t阶方阵N，在复数域内一定存在t个特征值，并且根据Collatz包含定理可以给出特征值的上下限。这个定理可简单地叙述如下［15］：

命x是任取的一个列向量（在实际应用中x当然应该是一个恰当地选取的列向量）。记y＝Nx，设x、y的各个元素为

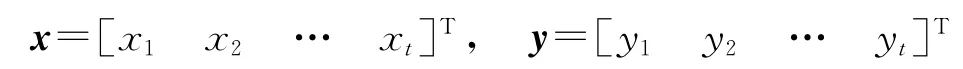
再记

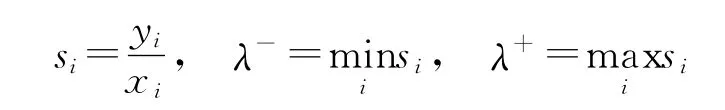
Collatz包含定理断定，在区间

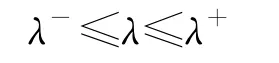
内至少存在一个方阵N的特征值。

根据Collatz包含定理可以证明如下定理。

定理1：法矩阵存在复共线性时，一定存在相对于法矩阵元素绝对值很小的特征值。

证明：令N＝［N1N2…Nt］如果法矩阵N存在一个复共线性关系，不妨仍设存在复共线性关系的几列为Ni1、Ni2、…、Nir，则Ni1、Ni2、…、Nir之间存在近似的线性关系，即存在不完全为零的一组数bi1、bi2、…、bir，使得

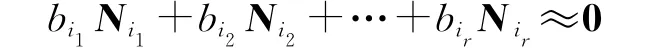
故向量bi1Ni1＋bi2Ni2＋…＋birNir中，各元素的绝对值远小于法矩阵中元素绝对值。令Collatz包含定理中的向量x的元素为

则y＝Nx≈0，故λ－和λ＋均是相对于法矩阵元素绝对值很小的实数，因此在区间［λ－，λ＋］中至少存在一个相对于法矩阵元素绝对值很小的特征值。证毕。

不妨仍记这个相对于法矩阵元素绝对值很小的特征值为λ1。在测量数据处理中，一般设计矩阵只会存在少数的几个复共线性关系，即不会出现法矩阵的t个特征值均很小的情况。故λt是一个大小正常的特征值，所以λt相对于λ1会很大，则条件数λt／λ1很大。

另外，由2.1中论述和定理1可得以下定理。

定理2：法矩阵存在相对于本身元素绝对值小得多的特征值是法矩阵存在复共线性的充分必要条件。

3.2 条件数很大不一定存在复共线性关系

根据定理2可知：若不存在相对于法矩阵元素绝对值很小的特征值，则法矩阵不存在复共线性。所以条件数大是由于λt远大于λ1引起的，并不表示法矩阵中一定存在复共线性关系。

4 无复共线性时条件数大对LS估计的影响

当法矩阵存在复共线性关系时，观测误差对LS估计的影响很大，这已经得到很多专家学者的认可，此处不再进行相关讨论。本节只讨论无复共线性关系时，条件数很大对LS估计有什么影响。

首先讨论特征值和特征向量的几何意义。方阵的特征向量是经过矩阵变换后保持方向不变，只是进行长度伸缩的向量，而特征值反映了特征向量在矩阵变换时的伸缩倍数。另外由谱定理［16］（spectral theorem）知道，一个方阵完全可以由它的特征向量表示，特征值即是矩阵在对应特征方向的贡献率大小。于是一个矩阵完全可以由特征值和特征向量组成的“特征”来表示。

如果法矩阵不存在复共线性，但是条件数很大，只是说明法矩阵在某个特征方向的特征明显，并不会放大观测误差对LS估计的影响。详细分析如下。

4.1 不考虑观测误差

线性模型（1）的法方程为

易知法矩阵的t个特征向量是线性无关的，可构成t维空间的一组基，故可设法方程中＾X由其线性表示为

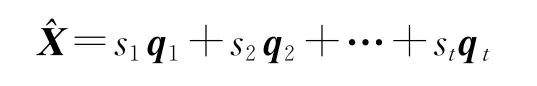
故

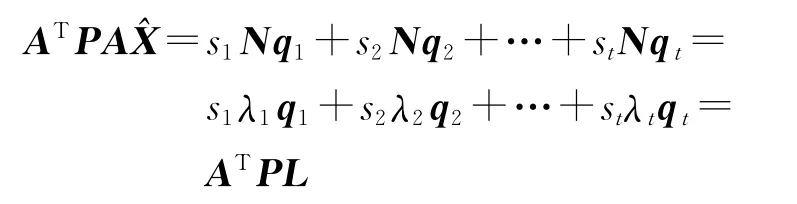
由上式可以看出，法矩阵的条件数比较大，只是把待估参数＾X变成与方向qt接近的向量ATPL，即把＾X拉向了法矩阵特征最明显的特征方向。

法矩阵病态性对LS估计的影响主要施加在法矩阵求逆阶段，同理条件数很大对LS估计的影响也主要在法矩阵求逆阶段。通过法方程可以得到LS估计的表达式为

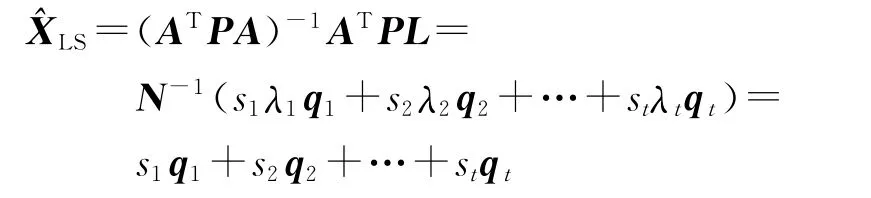
因此不考虑观测误差时法方程的求解是纯数学问题，可以得到严格的、准确的数学解。此处的法矩阵不存在复共线性，实际上通过上式还可以看出，即使法矩阵存在复共线性，只要观测值很准确，依然可以通过法方程得到准确的LS估计。

4.2 考虑观测误差

由于法矩阵不存在复共线性，则没有相对于法矩阵元素很小的特征值，此处条件数大是由于λt相对于λ1很大引起的，因此只讨论λt和qt对LS估计的影响。设ATPL在stλtqt方向存在小的误差Δtqt，其中Δt是一个小的数，则

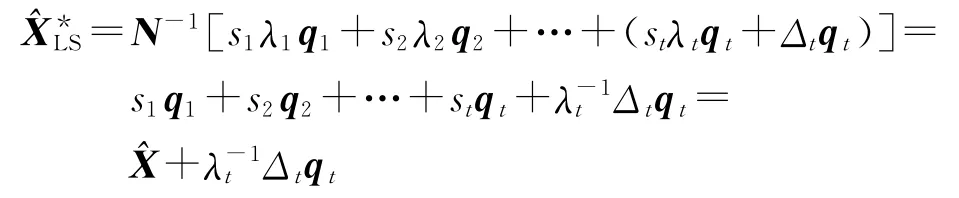
由于λt很大，故其倒数λ－1t很小，故λ－1tΔtqt很小，所以观测误差没有被放大。

5 双k型岭估计

采用上述改进的特征分析法，可以准确地判断复共线性的个数，并且可以判断每个复共线性具体存在于设计阵中的那几列。确定复共线性关系后，需要克服复共线性对估计值的影响。线性模型（1）的 LS估计和岭估计［17－21］分别为

式中，k＞0为普通岭估计的岭参数。

对于GPS快速定位中的双差模型，已经证明其病态性是由于在设计阵中，模糊度系数所在列可以近似线性表示出坐标改正数系数所在列造成的［20－21］。笔者针对GPS快速定位中的双差模型中病态性特征，提出了双k型岭估计［20－21］为

式中，K′＝diag（k′1，k′1，k′1，k′2，…，k′2）为对角矩阵，k′1＞0和k′2＞0为双k型岭估计的两个岭参数。易知，LS估计和普通岭估计为双k型岭估计的特例。

根据改进的特征分析法，可以准确地判断出法矩阵中具体那几列之间存在复共线性关系。由此复共线性关系提出新的相应的双k型岭估计如下

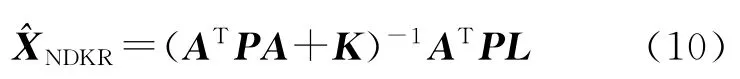
式中，K为对角矩阵，对角线元素由两个岭参数k1、k2（k1＞k2＞0）组成，k1和k2的排列顺序由法矩阵中确切的复共线性关系确定。不妨假设i1＜i2＜…＜ir列之间存在复共线性关系，其中1≤i1，ir≤t，则K中对角线上第i1、i2、…、ir个元素为岭参数k1，其余的对角元素取岭参数k2，即法矩阵中存在复共线性关系的几列对应比较大的岭参数k1，其余的列对复共线性贡献很小对应岭参数k2。

合理地确定k1和k2是一个应用上十分重要的问题。注意到双k型岭估计是广义岭估计的特例，故应用从广义岭估计出发确定普通岭估计中岭参数的思想［22］确定k1和k2。

利用文献［17］公式，两个岭参数k1和k2分别取为

式中，α＝［α1α2…αp］T＝QTX为原参数向量X的典则参数Λ＝diag（λ1，λ2，…，λt），V＝－L，0＜c＜1。

当模型存在复共线性时，双k型岭估计可以有效地克服病态性影响。当模型不存在复共线性关系时，双k型岭估计退化为LS估计。

6 算例与分析

算例1：仿真线性模型。对于设计阵只包含一个复共线性关系的情况，改进的特征分析法可以很容易地判断出复共线性情况，此处不再讨论。讨论复杂的设计阵数据列之间存在两个复共线性，并且两个复共线性关系相互影响的情况。例如，设计阵为

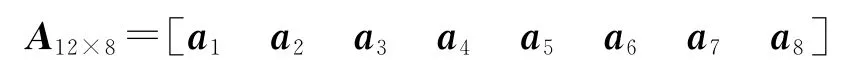
用下列两个表达式构造设计阵的复共线性

式中，εi～N12（0，0.12E）。设法矩阵元素绝对值最小值为其中i，j＝1，2，…，t。则法矩阵的、法矩阵特征值λi的数值如表1所示。

表1 算例1的min（｜Nii｜）和λi 数值大小Tab.1 Numerical values of min（｜Nii｜）andλiof example 1

由表1可以看出，法矩阵存在2个复共线性。计算A12×8q1＝q11a1＋q21a2＋…＋q81a8，由于篇幅有限，给出矩阵［q11a1q21a2…q81a8］的前3行为

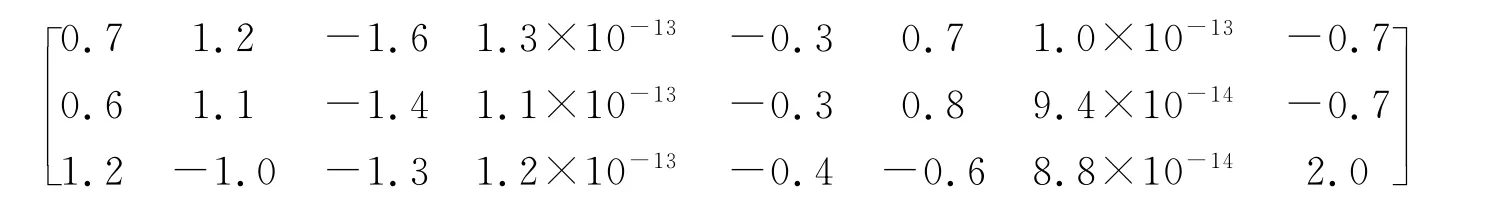
由此矩阵可以看出，第4、7列的元素值很小，故这两列不包含在复共线性之内。在设计阵中，第1、2、3、5、6、8列之间存在复共线性关系。最小特征值对应的特征向量q1为

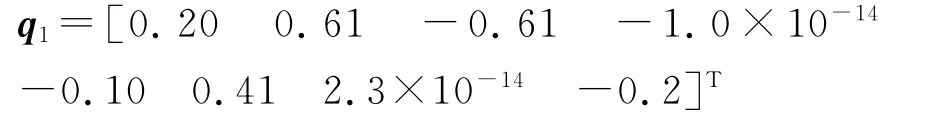
则［1 3.00 －3.00 0 －0.50 2.00 0 －1.00］T此系数与式（13）减去式（14）后的系数，即与

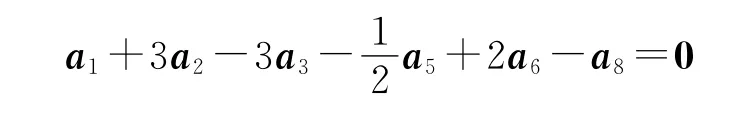
的系数是一致的。

考虑第2个复共线性。计算A12×8q2＝q12a1＋q22a2＋…＋q82a8，给出矩阵［q12a1q22a2…q82a8］的前3行为

由此矩阵可以看出，仍然是设计阵第1、2、3、5、6、8列之间存在复共线性关系，特征向量q2为

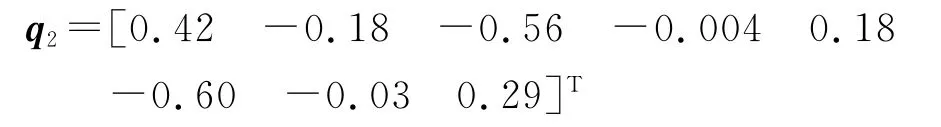
则

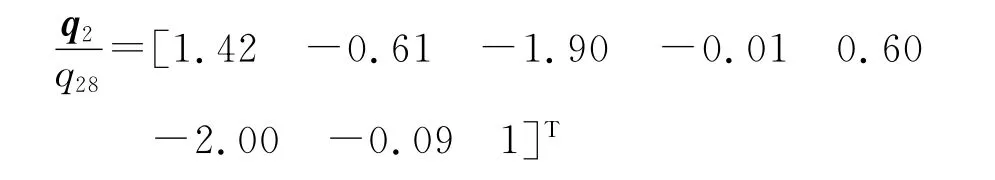
由于第2个复共线性较弱，此系数与表达式1.5×（13）＋（14），即与

的系数是近似一致的。

由以上分析可以看出，虽然设计阵中的复共线性关系是由式（13）、式（14）引起的，但是设计阵出现小的特征值或者法矩阵条件数很大不是因为这两个表达式中某一个造成的。设计阵的复共线性是这两个表达式共同作用的结果，并且这两个表达式的组合造成了一强一弱两个复共线性关系。

以估计值和真值差的模作为估计评价标准，则LS估计和本文提出的双k型岭估计的评价标准分别为26.477和2.715 9。双k型岭估计的估计效果远高于LS估计的估计效果。

算例2：设GEO卫星定点于160°E，3个模拟地面观测站为北京、三亚和成都，基本观测量是站星之间的单程测距，以均值为1m、方差为1的正态分布随机变量为随机误差，数据采样间隔为60s，初始历元的卫星位置三分量均附加10m固定偏差。采用动力法进行LS批处理定轨，待估状态向量X为初始历元的卫星位置和速度向量、2个光压参数η和、两个测站（三亚和成都）系统偏差参数、沿迹方向的2个周日周期经验力振幅观察上述矩阵可以很容易发现，矩阵［q11a1q21a2…qt1at］第1、2、3、4、9、10列元素绝对值较大。故其对此复共线性贡献较大，即这几列之间存在复共线性关系。这个结论也验证了GEO卫星轨道易受系统误差影响大的普遍看法［12－13］。根据此复共线性关系，令共12参数。定轨弧长从4h至3d，其中针对机动后轨道快速恢复的4h短弧跟踪条件只解算轨道6参数。

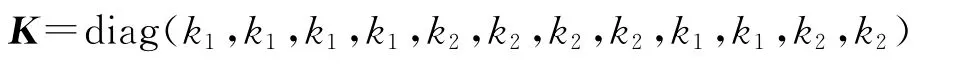
为考察复共线性对定轨弧长的敏感性，逐历元累加法矩阵。设法矩阵元素绝对值最小值为，其中i，j＝1，2，…，t。则6参数4h观测数据和12参数8h观测数据法矩阵的、法矩阵特征值λi的数值如表2所示。

表2 算例2的min（｜Nii｜）和λi 数值大小Tab.2 Numerical values of min（｜Nii｜）andλiof example 2

分析表2发现：

（1）采用6参数进行定轨时，法矩阵不存在复共线性。此处条件数大只是最大特征值和最小特征值之间的比值大，不会放大观测误差对估计值的影响。故采用LS估计即可得到很好的估计结果。

（2）采用12参数进行轨道确定时，法矩阵存在一个严重的复共线性关系，必须要克服此复共线性关系对估计值得影响。

对解算12参数的情况，下面采用特征分析法讨论复共线性具体存在于设计阵的那几列。由于观测历元较少时复共线性比较明显，此处采用前10个历元的设计阵A30×12进行分析。计算

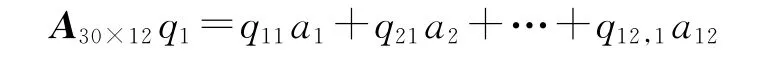
采用四舍五入方法给出第3个历元数据计算得到的矩阵［q11a1q21a2…q12，1a12］如下

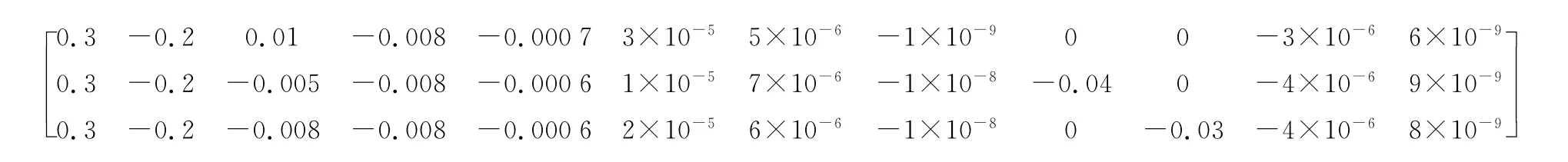
式中，k1和k2由文中相应的岭参数公式确定，c＝1／2。

由于GEO轨道的确定一般采用比较长的观测数据，随着观测数据的增加，复共线性会逐渐减弱。当存在复共线性时，采用双k型岭估计可以克服其影响；当不存在复共线性关系时，双k型岭估计退化为LS估计。故采取两种方案进行分析讨论：

方案1采用LS估计；

方案2采用本文提出的双k型岭估计。

以卫星位置的三维定轨误差绝对值的平均值为定轨评价标准。上述两种方案的位置误差随定轨弧长从4h（240历元）到3d（4320历元）的变化情况如图1所示。

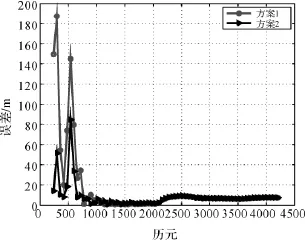
图1 算例2中方案1和方案2定轨误差Fig.1 Orbit error of scheme 1and scheme 2of example 2

由图1可以看出：

（1）当观测历元较少时，设计阵病态性比较严重，LS估计远不如双k型岭估计效果好。随着观测历元的增加，病态性逐渐减弱。在1000历元到2000历元之间病态性较弱，LS估计和双k型岭估计的结果相当，定轨误差均在5m以内。

（2）2000历元以后，由于观测历元增多，设计阵已不存在复共线性，此时双k型岭估计完全退化为LS估计，两种方案的定轨误差曲线完全重合。但是由于累积误差的影响，此时相应的定轨评价标准在10m以内。

6 结 论

（1）证明了以下定理：法矩阵存在复共线性与法矩阵存在相对于本身元素绝对值小得多的特征值是充分必要条件。

（2）给出了判断法矩阵是否存在小的特征值的方法，进而完善了特征分析法。

（3）若法矩阵存在复共线性，则条件数一定很大。若不存在相对于法矩阵元素绝对值很小的特征值，即使条件数很大，法矩阵本身也不存在复共线性。

（4）不存在复共线性时，条件数很大只是反映了法矩阵特征值差异较大，它不会放大观测误差对LS估计的影响。

（5）准确判断出法矩阵中具体那几列之间存在复共线性关系后，本文提出的相应双k型岭估计可以有效地克服复共线性的影响。采用从广义岭估计出发确定普通岭估计中岭参数的思想，给出了确定双k型岭估计中岭参数的合理方法。

（6）采用6参数对GEO卫星定轨时，法矩阵不存在复共线性。采用12参数对GEO卫星定轨时，当观测数据较少时复共线性很严重，随着观测时间的增加复共线性越来越弱，当观测时间为两天时法矩阵已完全不存在复共线性。

［1］ GUI Qingming，YAO Shaowen，GU Yongwei，et al.A New Method to Diagnose Multicollinearity Based on Condition Index and Variance Decomposition Proportion（CIVDP）［J］.Acta Geodaetica et Cartographica Sinica，2006，35（3）：210－214.（归庆明，姚绍文，顾勇为，等.诊断复共线性的条件指标－方差分解比法［J］.测绘学报，2006，35（3）：210－214.）

［2］ CHEN Xiru，WANG Songgui.Advanced Regression Analysis［M］.Hefei：Anhui Education Publishing House，1987.（陈希孺，王松桂.近代回归分析［M］.合肥：安徽教育出版社，1987.）

［3］ LU Xiushan.Analysis Theory on Ill－conditioned System with Applications in Surveying［D］.Wuhan：Institute of Geodesy and Geophysics of CAS，1999.（卢秀山.病态系统分析理论及其在测量中的应用［D］.武汉：中国科学院测量与地球物理研究所，1999.）

［4］ BELSLEY D A.Conditioning Diagnostics：Collinearity and Weak Data in Regression［M］.New York：Wiley，1991.

［5］ GUI Qingming，GUO Jianfeng，BIAN Shaofeng.Ill－conditioning Diagnostics Based on Eigensystem［J］.Science of Surveying and Mapping，2002，27（2）：13－15.（归庆明，郭建锋，边少锋.基于特征系统的病态性诊断［J］.测绘科学，2002，27（2）：13－15.）

［6］ GUO Jianfeng.Study on Diagonostics and Processing of Ill－Conditioning Adjustment System ［D］. Zhengzhou：Information Engineering University，2002.（郭建锋.测量平差系统病态性的诊断与处理 ［D］.郑州：信息工程大学，2002.）

［7］ GU Yongwei，GUI Qingming.Study of Regularization Based on Signal－to－noise Index in Airborne Gravity Downward to the Earth Surface［J］.Acta Geodaetica et Cartographica Sinica，2010，39（5）：458－464.（顾勇为，归庆明.航空重力测量数据向下延拓基于信噪比的正则化方法的研究［J］.测绘学报，2010，39（5）：458－464.）

［8］ MORAN K M，CICCI D A.Sensitivity of Ridge－type Estimation Methods to Condition Number［J］.Applied Mathematics and Computation，2000，112（1）：143－159.

［9］ LI Fei，HAO Weifeng，WANG Wenrui，et al.The Perturbation of Nonlinear Ill－conditioned Solution［J］. Acta Geodaetica et Cartographica Sinica，2011，40（1）：5－9.（李斐，郝卫峰，王文睿，等.非线性病态问题解算的扰动分析［J］.测绘学报，2011，40（1）：5－9.）

［10］ XU Xinyu，LI Jiancheng，WANG Zhengtao，et al.The Simulation Research on the Tikhonov Regularization Applied in Gravity Field Determination of GOCE Satellite Mission［J］.Acta Geodaetica et Cartographica Sinica，2010，39（5）：465－470.（徐新禹，李建成，王正涛，等.Tikhonov正则化方法在GOCE重力场求解中的模拟研究［J］.测绘学报，2010，39（5）：465－470.）

［11］ JIANG Tao，LI Jiancheng，WANG Zhengtao，et al.Solution of Ill－posed Problem in Downward Continuation of Airborne Gravity［J］.Acta Geodaetica et Cartographica Sinica，2011，40（6）：684－689.（蒋涛，李建成，王正涛，等.航空重力向下延拓病态问题的求解［J］.测绘学报，2011，40（6）：684－689.）

［12］ GUO Rui，ZHOU Jianhua，HU Xiaogong，et al.A New Strategy of Rapid Orbit Recovery for the Geostaionary Satellite［J］.Acta Geodaetica et Cartographica Sinica，2011，40（sup）：19－25.（郭睿，周建华，胡小工，等.一种地球静止轨道卫星轨道快速恢复定轨方法［J］.测绘学报，2011，40（sup）：19－25.）

［13］ DU Lan.A Study on the Precise Orbit Determination of Geostationary Satellites［D］.Zhengzhou：Information Engineering University，2006.（杜兰.GEO卫星精密定轨技术研究［D］.郑州：信息工程大学，2006.）

［14］ ZHENG Zhaobao.A Solving Method of Ill Condition Equation in the Photogrammetry［J］.Acta Geodaetica et Cartographica Sinica，1987，16（3）：198－203.（郑肇葆.摄影测量中病态方程求解问题［J］.测绘学报，1987，16（3）：198－203.）

［15］ COLLATZ L.Einschlie Bungssatz Für Die Charakteristischen Zahlen von Matrizen［J］. Mathematische Zeitschrift，1942，48（1）：221－226.

［16］ ZHANG Xianda.Matrix Analysis and Applications［M］.Beijing：Tsinghua University Press，2004.（张贤达.矩阵分析与应用［M］.北京：清华大学出版社，2004.）

［17］ HOERL AE，KENNARD RW.Ridge Regression：Biased Estimation for Non－orthogonal Problems［J］.Technometrics，1970，12（1）：55－58.

［18］ GUI Q M，LIU J S.Biased Estimation in Gauss－Markov Model［J］.Allg Verm.－Nachr，2000，107：104－108.

［19］ LIU L L，LIU J Y.Study of the Implementation of GPS Rapid Positioning Based on Ridge Estimation Theory［J］.Telemetry and Telecontrol，2004，25（4）：1－4.（刘立龙，刘基余.基于岭估计理论实现GPS快速定位研究［J］.遥测遥控，2004，25（4）：1－4.）

［20］ GUI Qingming，HAN Songhui.A New Algorithm of GPS Rapid Positioning Based on DoublekType Ridge Estimation［J］.Journal of Surveying Engineering，2007，133（4）：173－178.

［21］ HAN Songhui，GUI Qingming，MA Chaozhong.Robust DoublekType Ridge Estimation and Its Applications in GPS Rapid Positioning［C］∥ VI Hotine－Marussi Symposium on Theoretical and Computational Geodesy. Berlin：Springer，2008：243－247.

［22］ KIBRIA B W G.Performance of Some New Ridge Regression Estimators［J］.Communications in Statistics－Simulation and Computation，2003，32（2）：419－435.