模糊判断矩阵的一致性检验

杨燕华，吕跃进

（广西大学a.电气工程学院；b.数学与信息科学学院，南宁530004）

0 引言

层次分析法（AHP）[1，2]中，决策者通过对同一层次中两两因素的比较得到判断矩阵，并由判断矩阵得到该层次各因素的排序权重向量。判断矩阵的一致性及一致性检验标准影响着最终的排序结果。美国运筹学家Saaty教授提出了用平均随机一致性指标RI修正CI的方法，并给出1至13阶矩阵的RI值。这一方法在AHP中被普遍接受和应用。

由于客观事物的复杂性、决策者自身的局限性，一些学者把模糊数学的思想和方法引入到层次分析法中，提出模糊层次分析法（FAHP），将AHP中构造的正互反判断矩阵转为构造模糊互补判断矩阵[3-5]。对于模糊互补判断矩阵的一致性问题，目前尚无统一的检验方法，有文献提出不同检验的方法。文献[6]给出关于互补判断矩阵满意一致性的定义，通过建立可达矩阵给出互补判断矩阵满意一致性的判定方法，但该方法只粗略地考虑了因素重要性的次序一致性，没有考虑重要性程度的一致性；文献[7]定义了一个衡量模糊判断矩阵加性一致性程度的指标，但并没有规范地给出所定义的一致性检验指标小于何阈值时，判断矩阵能通过一致性检验。

本文通过加性一致性条件的数学变换，定义了一个模糊一致性检验指标，通过MATLAB仿真实验构造足够数量的n阶随机模糊互补判断矩阵，并计算平均随机模糊一致性指标，得到模糊一致性比率，给出不同阶数下判断矩阵通过一致性检验的条件。

1 模糊互补判断矩阵

定义1[8]：设矩阵R=(rij)n×n，若有0≤rij≤1，则称矩阵R是模糊矩阵。

定义2[8]：设模糊矩阵R=(rij)n×n，若有rij+rji=1，则称矩阵R是模糊互补矩阵。

定义3[8]：设模糊互补矩阵R=(rij)n×n，若对任意k，均有rij=rik-rjk+0.5，则称矩阵R是模糊一致矩阵。

定理1[9]：设R是n阶模糊矩阵，则R是模糊一致矩阵的充分必要条件是存在一n阶非负归一化的向量W=(w2，…，wn)T及一正数a，使得∀i，j，有下式成立：

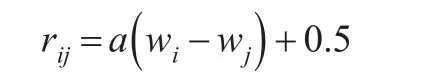
上式等号两边同时对j求和，得：

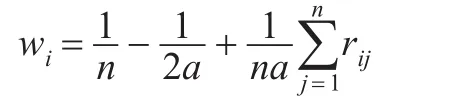
文献[9]已经给出a的一个判断，a越小表明决策者非常重视元素之间的差异，a越大表明决策者不是非常重视元素间重要程度的差异。在实际应用中，认为应取a=(n-1)/2。

2 模糊一致性指标FCI及一致性检验

模糊互补判断矩阵R中的任意一个元素rij反映的是两个待选方案i和j之间的重要程度之比，可以通过两个方案的直接比较得到。矩阵R一致的充分必要条件是rij=a()wi-wj+0.5成立。但在实际进行两两比较判断时，由于信息的不完备性以及人类思维的局限性，一般情况下R很难达到一致，即所以，对i，j，有：

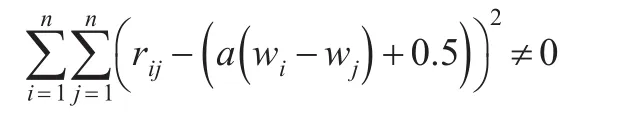
对于上式，本文认为模糊互补判断矩阵R与一致性矩阵的偏差在一定范围之内是可以接受的，当矩阵R越接近一致性矩阵时，可接受的程度越高。

又因为矩阵R的互补性，有rii=0.5，当i=j时，，因此主对角元素对于矩阵R是否一致没有影响。

综上分析，本文给出模糊互补判断矩阵R的一个模糊一致性检验指标FCI。

称FCI为模糊互补判断矩阵R的模糊一致性指标。FCI表示rij对矩阵R不一致的贡献程度。

又由于矩阵R是互补的，有下面等式成立：上式表明，计算R的模糊一致性指标FCI只需要考虑矩阵的上三角元素。

定理2：模糊互补判断矩阵R=(rij)n×n是一致性矩阵的充分必要条件是FCI=0。

FCI用来衡量模糊互补判断矩阵R与一致性矩阵的偏差程度，FCI为0表示R与一致性矩阵没有偏差，FCI越大表示R的一致性越差。若FCI的值在某一可接受的范围之内，认为矩阵R是满意一致的。

定义5：设模糊互补判断矩阵R=(rij)n×n，当FCI≤c（c为常数），称R是满意一致的。

定义6：平均随机模糊一致性指标FRI是指多个同阶随机互补判断矩阵的模糊一致性指标FCI的平均值。

根据平均随机模糊一致性指标FRI的思想，构造数量足够、且在0.1～0.9模糊标度下的n阶平均随机互补判断矩阵，分别计算其FCI值，最后得到FCI的平均值即为FRI。其计算过程如下：

步骤1：从0.1～0.9模糊标度共9个数中随机均匀取值，作为矩阵R的上三角元素，主对角元素取0.5，下三角元素取1减去对应位置的上三角元素，构成n阶随机模糊互补判断矩阵；

步骤2：计算所得随机模糊互补判断矩阵的模糊一致性指标FCI；

步骤3：重复上述步骤得到足够多的随机矩阵，计算样本均值。

这个均值就是平均随机模糊一致性指标FRI，是与阶数n相关的数值。通过Matlab编码实现上述过程。为了保证得到更精确的平均随机模糊一致性指标，迭代次数均为10000次，即分别构造10000个n阶随机模糊互补矩阵（这里仅列出阶数n为3至20阶）。结果见表1。

表1 3至20阶模糊互补判断矩阵的平均随机一致性指标表

对模拟计算结果分析做出样本频率分布图，如图1（曲线从左至右分别代表4至9阶）。

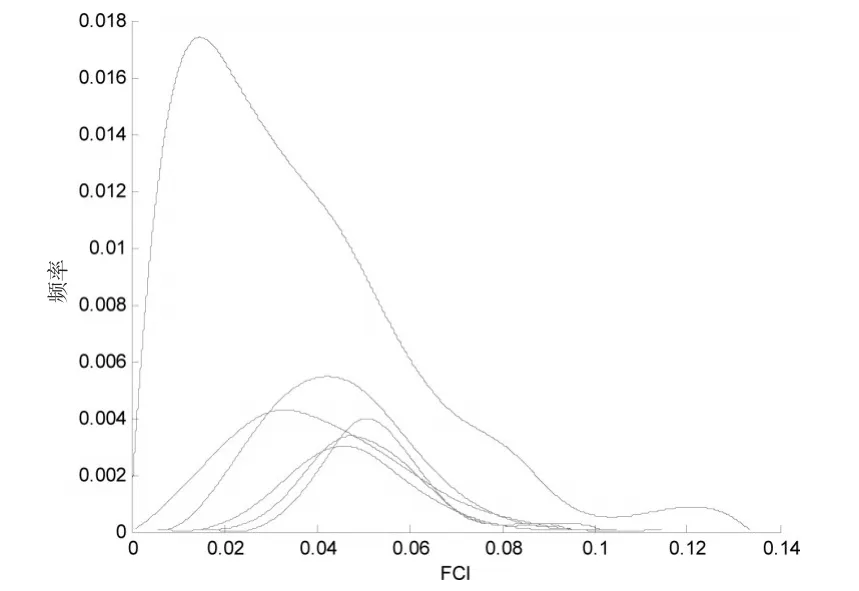
图1 不同阶数（4至9阶）随机模糊互补矩阵FCI值分布图

当n>3时，FCI的样本频率近似为正态分布。当n=7阶时，频率曲线在FCI=0.0498附近达到最高峰；当n=8阶时，频率曲线在FCI=0.0464附近达到最高峰；当n=9阶时，频率曲线在FCI=0.0514附近达到最高峰。

FRI值随着阶数增大而增大，但总体上趋于一个稳定值。进一步实验表明，当阶数足够大，超过500阶时FRI基本趋于0.0666。

定义7：模糊一致性指标FCI与同阶的平均随机模糊一致性指标FRI的比值，称为模糊一致性比率，记为：

用模糊一致性比率FCR检验矩阵的一致性，FCR越小，矩阵的一致性越好。根据Saaty的判断思想，决策者有意识构造的判断矩阵要比随机构造的判断矩阵至少优十倍，因此，一般认为，FCR≤0.1，模糊互补判断矩阵符合满意的一致性标准，得到的层次单排序的结果是可以接受的，否则需要修正判断矩阵，直到检验通过。

下面给出算例。由表1知4阶矩阵的平均随机模糊一致性指标FRI(4)=0.0335。

3 与文献[6]、文献[7]的比较分析

下面利用文献[6]、文献[7]中的算例进行比较分析。

（1）利用文献[6]的方法，计算R的可达矩阵为：

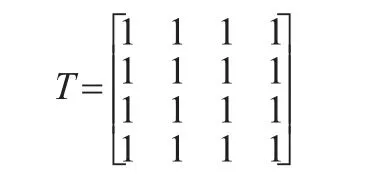
T对角线上存在为1的元素，可知矩阵R不一致。但是文献[3]计算可达矩阵的方法，只是在逻辑关系上考虑了不同因素之间的优越关系，不能体现元素之间重要性程度或优越性程度的一致性。

（2）利用文献[7]定义的加性一致性指标

计算R的加性一致性指标为ρ=0.5。文献[4]直接假设一个阈值ε=0.2，认为ρ=0.5＞ε，故矩阵R一致性较差，没有给出ε取值的理论依据。这也是很多文献[10，11]在定义一致性指标时存在的不足，并没有规范地给出通过一致性检验的阈值。

（3）利用本文定义的模糊一致性指标计算得FCI=0.0525，通过与仿真实验得到的平均随机一致性指标进行比较，检验一致性比率FCR=1.5672＞0.1。结果与文献[6]、文献[7]一样，矩阵R不通过一致性检验，且一致性较差。

4 结束语

本文通过定义模糊一致性指标，仿真实验给出平均随机模糊一致性指标，其比值用以衡量判断矩阵是否通过一致性检验，具有一定理论意义。本文的后续工作将是提出更具一般性的模糊互补判断矩阵的一致性检验指标，而不仅仅局限在加性一致上，并深入研究检验条件FCR≤0.1与矩阵阶数的关系。

[1] Saaty T L.The analytic hierarchy process[M].New York:McGraw-Hill,1980.

[2] 王莲芬,许树柏.层次分析法引论[M].北京:中国人民出版社,1989.

[3] Orlovsky S A.Decision-making With a Fuzzy Preference Relation[J].Fuzzy Sets and Systems,1978,(1).

[4] Tanino T.Fuzzy Preference Orderings in Group Decision Making[J].Fuzzy Sets and Systems,1984,33(84).

[5] Chiclana F,Herrera F,Herrera-Viedma E,et al.A Classification Method of Alternatives for Multiple Preference Ordering Criteria Based on Fuzzy Majority[J].Journal of Fuzzy Mathematics,1997,4(4).

[6] 樊治平,姜艳萍.互补判断矩阵一致性改进方法[J].东北大学学报：自然科学版,2003,24(1).

[7] 宋光兴,杨德礼.模糊判断矩阵的一致性检验及一致性改进方法[J].系统工程,2003,21(1).

[8] 姚敏,张森.模糊一致矩阵及其在软科学中的应用[J].系统工程,1997,15(2).

[9] 吕跃进.基于模糊一致矩阵的模糊层次分析法的排序[J].模糊系统与数学,2002,16(2).

[10] 和媛媛,周德群,王强.基于模糊判断矩阵的一致性调整方法[J].系统工程与电子技术,2001,30(11).

[11] 杨静,邱菀华.模糊互补判断矩阵一致性检验和改进方法研究[J].控制与决策,2009,24(6).