双因素方差分析方法的比较

戴金辉，韩存

（山东工商学院a.统计学院；b.价格指数研究中心，山东烟台264005）

0 引言

考虑两个类别自变量对数值因变量影响的方差分析称为双因素方差分析。在进行分析时有两种情况：一是只考虑两个影响因素对因变量的单独影响，这时的方差分析称为无交互效应的双因素方差分析；二是除了两个影响因素外，还考虑两个影响因素的搭配对因变量产生的交互效应，这时的方差分析称为有交互效应的双因素方差分析。经常有人把有交互效应的双因素方差分析或者无交互效应的双因素方差分析模型直接应用，本文探讨有交互效应双因素方差分析与无交互效应的双影响因素方差分析在应用上的区别。

1 有交互作用的双因素方差分析模型

双因素方差分析的数据结构见表1。

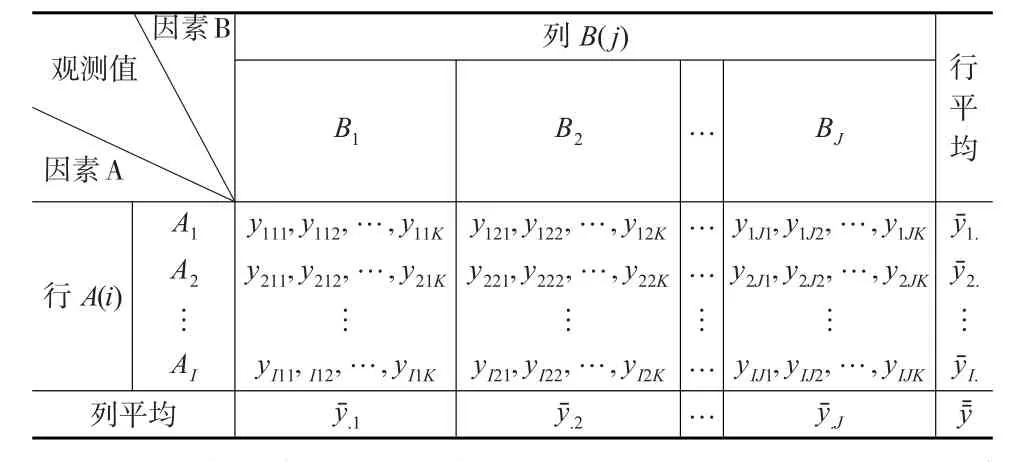
表1 双因素方差分析数据结构表

设影响因素A有I个水平，影响因素B有J个水平。两个影响因素共有IJ种不同的水平组合。如果每种水平组合只测得一个观测值，则有IJ个观测值，这样的测量属于无重复测量（无重复实验）。如果每种水平组合测得多个观测值，这样的测量就是重复测量（重复实验）。如果每种水平组合重复测量的次数相同，那么将重复次数记为K(K≥2)，这时两个影响因素的IJ种不同水平组合共有IJK个观测值。

为方便接下来的表述，引进下列表示符号：

μ：总均值，它是所有水平的均值μij的平均。

αi：影响因素A的效应。它衡量的是影响因素A的第i个水平均值与总均值的差异程度，即αi=-μ。

βj：影响因素B的效应。它衡量的是影响因素B的第j个水平均值与总均值的差异程度，即βj=-μ。

γij：影响因素A的第i个水平和影响因素B的第j个水平搭配产生的交互效应。它衡量的是影响因素A的第i个水平和影响因素B的第j个水平搭配(共有IJ个)对因变量产生的效应。

εijk：随机误差。反映随机因素对因变量的影响。

这样，对于任何一个观测值yijk，都可以表达成下面的线性组合，即：

yijk=μ+αi+βj+γij+εijk

其中i=1，2，…，I;j=1，2，…，J;k=1，2，…，K

yijk表示影响因素A的第i个水平和影响因素B的第j个水平组合的第k个观测值；μ表示不考虑影响因素A和影响因素B的影响时，观测值总的平均值，它是模型的常数项（截距）；αi表示影响因素A的水平为i时对观测数据的附加效应，它所对应的就是影响因素A的水平误差；βj表示影响因素B的水平为j时对观测数据的附加效应，它所对应的就是影响因素B的水平误差；γij表示影响因素A的第i个水平和影响因素B的第j个水平搭配产生的交互效应；εijk表示影响因素A的第i个水平和影响因素B的第j个水平组合中的第k个观测值的随机误差，同时假定εijk服从均值为0，方差为常数的正态分布。

有交互作用方差分析过程：

（1）对于影响因素A的I种水平和影响因素B的J种水平，要检验影响因素A的效应，影响因素B的效应、两个影响因素的交互效应，也就是检验下面的假设：

H0A:αi=0(i=1，2，…，I)（影响因素A的水平效应不显著）

H1A:αi(i=1，2，…，I)至少有一个不等于0（影响因素A的水平效应显著）

检验影响因素B的假设：

H0B:βj=0(j=1，2，…，J)（影响因素B的水平效应不显著）

H1B:βj(j=1，2，…，J)至少有一个不等于0（影响因素B的水平效应显著）

检验交互效应的假设：

H0AB:γij=0(i=1，2，…，I;j=1，2，…，J)（影响因素A与影响因素B交互效应不显著）

H1AB:γij(i=1，2，…，I;j=1，2，…，J)至少有一个不等于0(影响因素A与影响因素B交互效应显著）

（2）检验上述假设时,与模型yijk=μ+αi+βj+γij+εijk相应的误差分解示意图，见图1。

图1 有交互作用的双因素方差分析误差分解

根据上述误差分解原理，可以构建用于检验的统计量FA，FB，FAB。

设yijk表示影响因素A的第i个水平和影响因素B的第j个水平组合的第k个观测值，表示影响因素A的第i个水平的样本均值表示影响因素B的第j个水平的样本均值,表示影响因素A的第i个水平和影响因素B的第j个水平组合的样本均值，为全部IJK个观察值的总均值。

各平方和的计算公式如下：

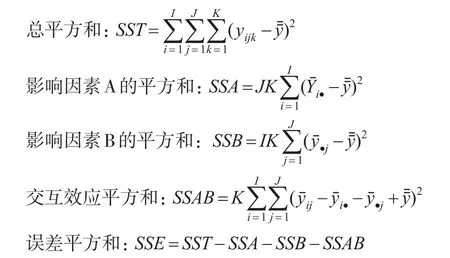
将各平方和除以相应的自由度df，得到各均方，再将各水平均方分别除以误差均方，即得到用于检验影响因素A、影响因素B、影响因素AB的统计量FA、FB、FAB,见表2所示。

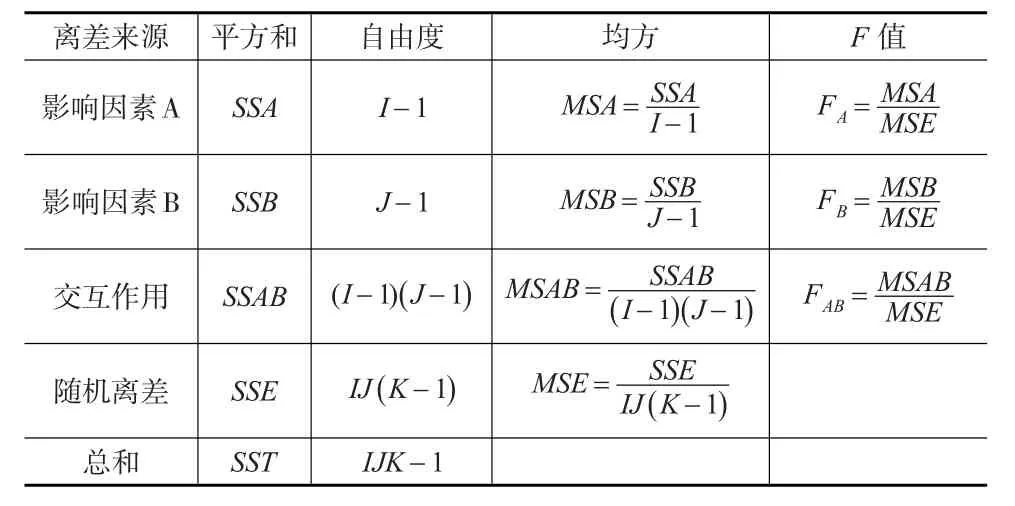
表2 有交互作用的双因素方差分析表

多重判定系数R2，它度量了影响因素A、影响因素B和两者交互作用AB对因变量的联合影响程度，R2的计算公式为：

R2数值越大，说明影响因素A、影响因素B和其交互作用AB对因变量的联合影响越大，随机误差平方和占总平方和的比例越小，说明影响因素A、影响因素B和其交互作用AB中的一个或者多个对因变量的变动有显著性的影响。

多重判定系数R2的平方根r（复相关系数）则反映了影响因素A、影响因素B和其交互作用AB联合起来与因变量之间的关系强度，r取值越大，说明影响因素A、影响因素B和其交互作用AB与因变量之间有较强的关系。

（3）根据给定的显著性水平α，查表，确定临界值Fα。（4）做出统计决策。

如果FA＞Fα，则拒绝原假设H0A，表明影响因素A对因变量的影响是显著的；反之，若FA＜Fα，则不拒绝原假设H0A，表明影响因素A对因变量无显著影响。

若FB＞Fα，则拒绝原假设H0B，表明影响因素B对因变量的影响是显著的；反之，若FB＜Fα，则不拒绝原假设H0B，表明影响因素B对因变量无显著影响。

若FAB＞Fα，则拒绝原假设H0AB，表明影响因素AB交互作用对因变量的影响是显著的；反之，若FAB＜Fα，则不拒绝原假设H0AB，表明影响因素AB交互作用对因变量无显著影响。

2 无交互效应双因素方差分析

当交互效应γij为0时，有交互作用的双因素方差分析模型就变为：

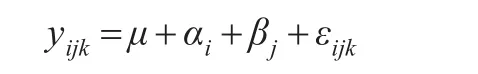
这是无交互效应双因素方差分析的数学模型，显然它是有交互效应的方差分析模型的一个特例。无交互作用方差分析过程：

（1）以前面对有交互作用双因素方差分析过程为基础，对于无交互作用的双因素方差分析就相对要简单了。对于影响因素A的I种水平和影响因素B的J种水平，要检验影响因素A的效应、影响因素B的效应，也就是检验下面的假设：

H0A:αi=0(i=1，2，…，I)（影响因素A的水平效应不显著）

H1A:αi(i=1，2，…，I)至少有一个不等于0（影响因素A的水平效应显著）

检验影响因素B的假设：

H0B:βj=0(j=1，2，…，J)（影响因素B的水平效应不显著）

H1B:βj(j=1，2，…，J)至少有一个不等于0（影响因素B的水平效应显著）

与有交互作用双因素方差分析的三种假设相比，变为两种假设。

（2）与有交互作用双因素方差分析的误差分析相比，无交互作用的双因素方差分析误差分解过程也变得简单，见图2。

图2 无交互作用的双因素方差分析误差分解

根据上述误差分解原理，可以构建用于检验的统计量FA，FB（见表3）。

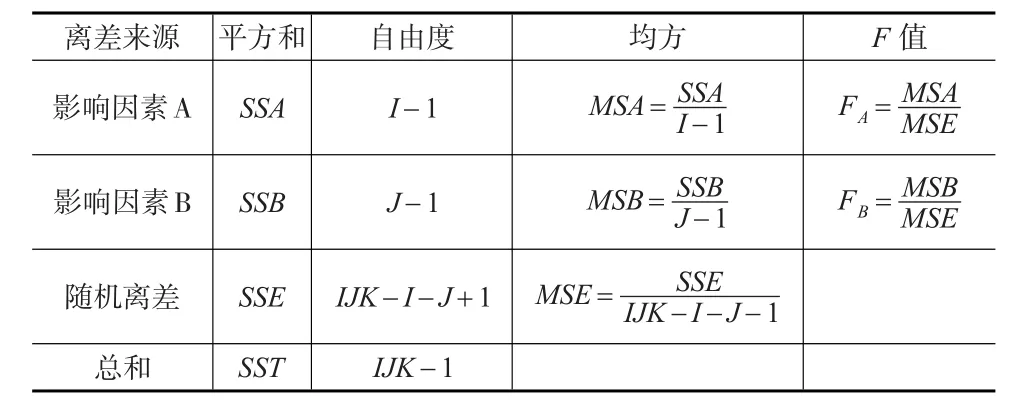
表3 无交互作用的双因素方差分析表

多重判定系数R2，它度量了影响因素A和影响因素B对因变量的联合影响程度，R2的计算公式为：

R2数值越大，说明影响因素A和影响因素B对因变量的联合影响越大，随机误差平方和占总平方和的比例越小，说明影响因素A和影响因素B有一个或者两个对因变量的变动有显著性的影响。

多重判定系数R2的平方根r（复相关系数）则反映了影响因素A和影响因素B与因变量之间的关系强度，r取值越大，说明影响因素A和影响因素B与因变量之间有较强的关系。

（3）根据给定的显著性水平α，查表，确定临界值Fα。

（4）做出统计决策。

如果FA＞Fα，则拒绝原假设H0A，表明影响因素A对因变量的影响是显著的；反之，若FA＜Fα，则不拒绝原假设H0A，表明影响因素A对因变量无显著影响。

若FB＞Fα，则拒绝原假设H0B，表明影响因素B对因变量的影响是显著的；反之，若FB＜Fα，则不拒绝原假设H0B，表明影响因素B对因变量无显著影响。

3 算例分析

假定有甲、乙两种施肥方式，3种小麦品种，搭配共有6种组合。如果选择30块地进行试验，则每种搭配进行5次试验，实验数据见表4。

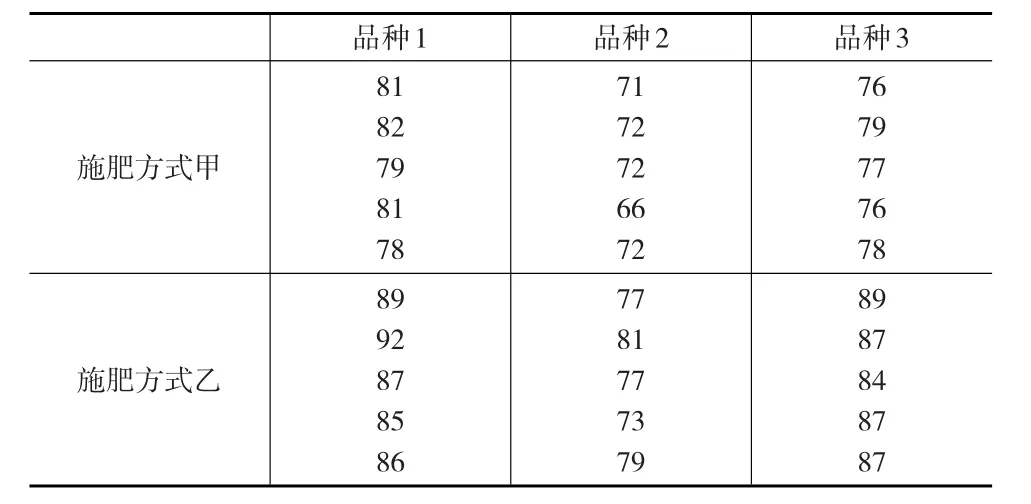
表4 小麦品种和施肥方式的实验数据

检验小麦品种、施肥方式和小麦品种与施肥方式交互作用对产量的影响。

解：这是一个双因素（2×3水平）的实验问题，并且每个因素的搭配各做了5次观察，所以是等重复的双因素方差分析。

提出假设：

H0A:施肥方式对小麦产量无显著影响

H1A:施肥方式对小麦产量有显著影响

H0B:小麦品种对小麦产量无显著影响

H1B:小麦品种对小麦产量有显著影响

H0AB:施肥方式和小麦品种搭配对小麦产量无显著影响

H1AB:施肥方式和小麦品种搭配对小麦产量有显著影响

数据经过统计分析软件SPSS计算后（与统计分析软件EXCEL计算结果会有一定差异），结果见表5。

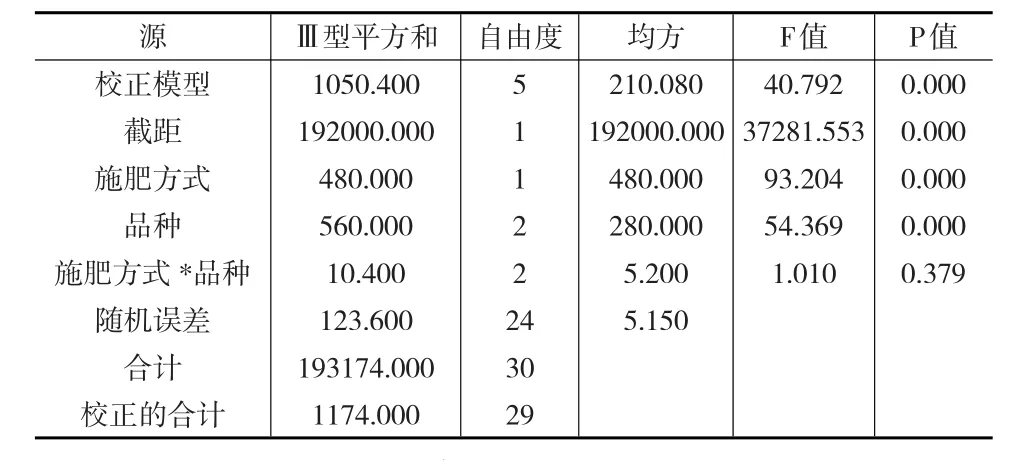
表5 有交互效应的双因素方差分析结果

有交互效应的双因素方差分析结果表明：施肥方式和品种两个因素对实验结果的影响是显著的，而施肥方式与品种的交互作用对实验结果的影响是不显著的。既然施肥方式与品种的交互作用对实验结果的影响是不显著的，可以对施肥方式与品种进行无交互作用的双因素方差分析，结果如表6所示。

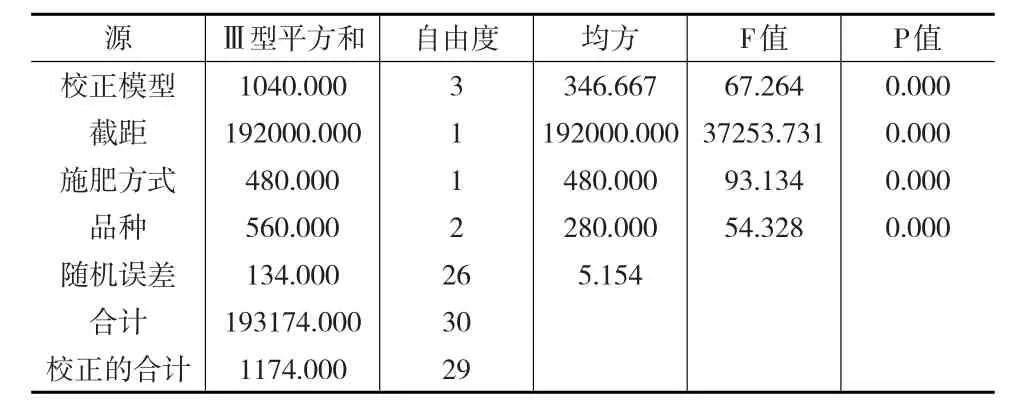
表6 无交互效应的双因素方差分析结果

无交互效应的双因素方差分析结果表明：施肥方式和品种两个因素对实验结果的影响都是显著的。

比较表5和表6，在有交互效应的双因素方差分析与无交互效应的双因素方差分析结果表明：施肥方式和品种在两种情况下的Ⅲ型平方和没有变，但是在有交互作用的双因素方差分析中，随机误差比无交互作用的双因素方差分析要小，并且有交互作用的双因素方差分析中，随机误差与交互作用平方和等于无交互作用的双因素方差分析中的随机误差，相应的F值会有稍许变化，但是不影响计算结果。

根据方差分析表可知，施肥方式对小麦产量影响显著；小麦品种对小麦产量影响显著；施肥方式和小麦品种搭配对小麦产量影响不显著。如果考虑施肥方式、小麦品种和两者的交互作用，判定系数R2=89.47%，而如果忽略了两者的交互作用，则判定系数为R2=88.59%，没有出现明显的降低。在经过检验施肥方式和小麦品种搭配对小麦产量无显著影响后，此题可以按照无交互作用的双因素方差分析进行解答。

4 结论

总结有两个影响因素时，考虑交互效应的方差分析与分别对两个影响因素做单因素方差分析是不同的。两个单因素方差分析实际上是假定两个影响因素间不存在交互效应，在两个影响因素间存在交互效应时可能会得出错误结论。因此，当有两个影响因素时，应首先考虑使用有交互效应的方差分析模型，当经过统计检验，交互效应不显著时，再考虑使用两个影响因素的单影响因素方差分析模型。

[1] 贾俊平.统计学——基于SPSS[M].北京：中国人民大学出版社，2014.

[2] 茆诗松，周纪芗.概率论与数理统计[M].北京：中国统计出版社，2007.

[3] 戴金辉,袁静.单因素方差分析与多元线性回归分析检验方法比较[J].统计与决策，2016,(9).

[4] 戴金辉，代金辉.方差分析在跳水运动员成绩管理中的应用[J].统计与决策，2016,(22).

[5] 戴金辉.单因素方差分析中异方差的检验与修正[J].统计与决策，2017,(8).