语音信号传输过程中的阈上随机共振现象

王 杰，王友国，翟其清

(南京邮电大学 理学院，江苏 南京 210046)

0 引 言

语音是人们在日常生活中进行交流沟通的主要媒介，因此语音传输就成为人与人之间信息传输的重要方式。随着信息技术的快速发展，语音通讯技术被广泛应用[1-3]。然而，在语音信号传输的过程中，信号不可避免地会受到来自外界和内部噪声的影响，这就使得获取到的语音信号存在失真的情况。为此学者们一直致力于寻找降噪、去噪的方法来提高语音信号的传输效率。但有些学者发现，噪声能够起到辅助信号传输的作用。文献[4]讨论了语音信号在二元输出的单阈值系统中，适当的加性噪声能够改善语音信号的传输，这种现象被称为阈上随机共振。

2000年，Stocks[5]研究了单阈值网络系统中的阈上随机共振现象。2015年，McDonnell等人[6]基于其在2009年提出的随机池网络模型[7]，以互信息为测度研究了在加性噪声下的具有多元输出的阈值系统中的阈上随机共振现象。Cheng等人[8]研究了在乘性噪声作用下，分别以互信息和信噪比为测度的具有多元输出阈值系统中的阈上随机共振现象。陈楠等人[9]以互信息为测度，研究了在加性和乘性噪声共同作用下的多阈值系统中的阈上随机共振现象。目前，阈上随机共振的研究已经得到了广泛的应用[10-18]，如参数信号的估计任务[13]、信号重构[14]、图像恢复[18]等。

该文在文献[4,9]的基础上，选取相关系数为测度，研究其在受到加性和乘性噪声共同作用下的具有多元输出阈值系统中的阈上随机共振现象。此外还用真实语音信号作为输入进行仿真来验证在一定噪声强度范围内，语音信号在传输过程中能够发生阈上随机共振现象。

1 阈值系统中的语音信号传输

1.1 阈值系统

该文采用多阈值网络模型作为语音信号传输系统，它包含N个阈值单元，如图1所示[9]。

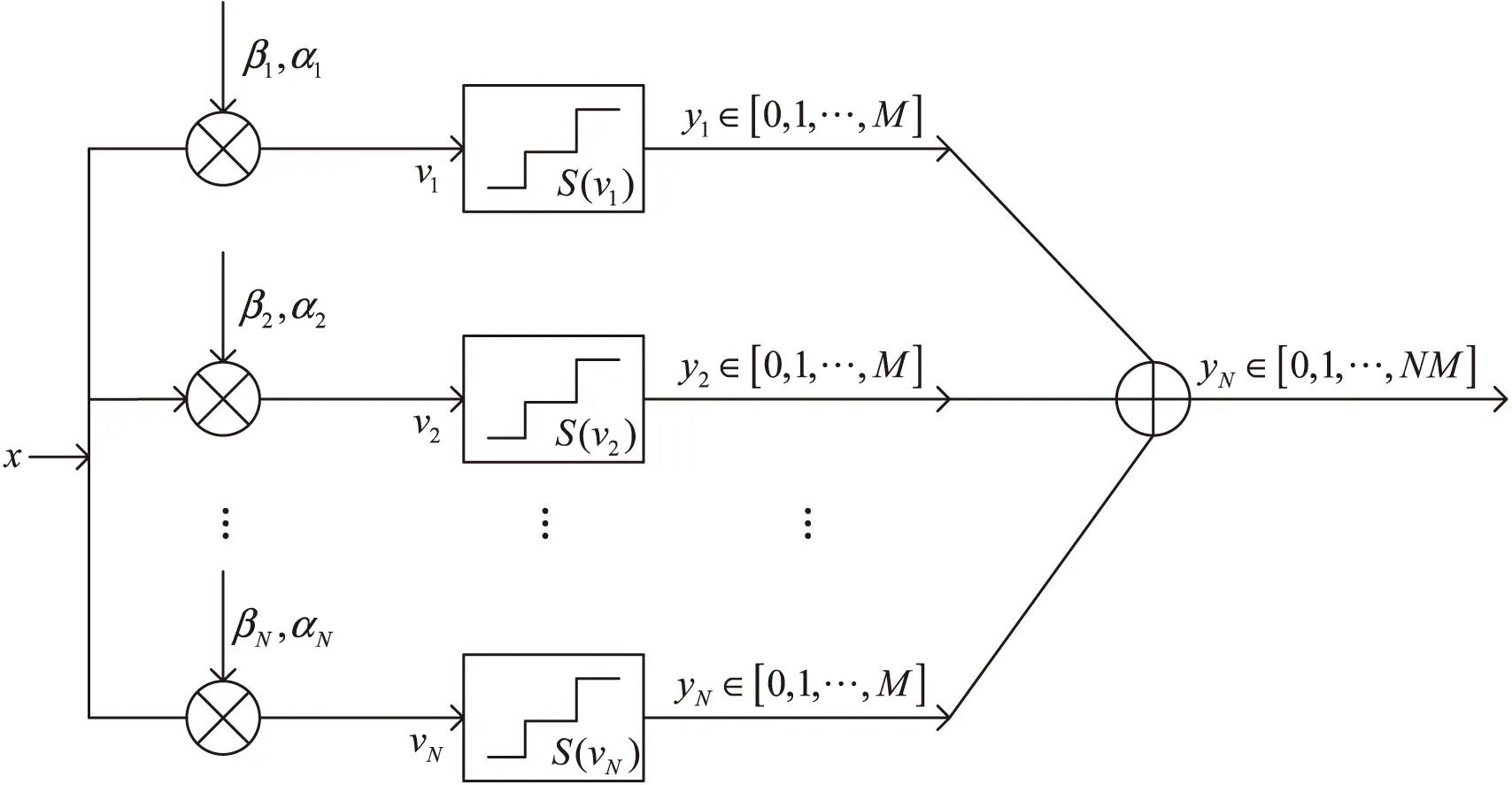
图1 多阈值网络系统模型

文献[19]通过实验评估证明，语音信号的统计量类似于多元拉普拉斯。拉普拉斯在去相关域中准确地描述了所有语音的边缘分布。尽管语音成分的能量是随时间变化的，但它们的分布形状仍然是拉普拉斯式的。因此，用拉普拉斯分布可以很好地描述语音样本的分布。在图1的阈值系统中，输入信号x选择均值为0、方差为σ2的拉普拉斯信号，其概率密度函数为：

(1)

αi、βi分别为标准高斯加性噪声和标准高斯乘性噪声，且二者相互独立，即：

〈αi,αj〉=0,〈βi,βj〉=0,i≠j,且〈αi,βj〉=0,

i=1,2,…,N,j=1,2,…,M

(2)

经噪声作用后的第i个阈值单元的输入为：

vi=x+Dβix+Qαi

(3)

其中，D和Q分别为乘性噪声强度和加性噪声强度，当D→0时，系统中仅受到加性噪声作用，当Q→0时，系统中仅受到乘性噪声作用。vi的条件概率可表示为：

P(vi|x)=

(4)

该模型的每个阈值单元均有M个阈值θi,j，其中i=1,2,…,N,j=1,2,…,M。规定θi,0=-∞,θi,M+1=+∞。为了便于计算，不妨假设每个阈值单元的阈值在[0,1]上服从均匀分布，且每个阈值单元的阈值相等，即有：

θ1,j=θ2,j=…=θN,j,j=1,2,…,M

(5)

每个阈值单元的输出为：

(6)

每个阈值单元的输出条件概率为：

(7)

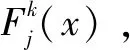
(8)

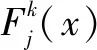
(9)

文献[20]即为文中阈值输出元数M=2，乘性噪声强度D=0时的情况。

1.2 相关系数

取相关系数作为语音信号传输的测度[4]，当输入信号为x，输出信号为y时，相关系数为：

(10)

由式(1)，E(x)=0，故上式化简为：

(11)

其中，

(12)

(13)

1.3 数值计算与结果分析

该文取信号x的标准差σ=1。利用式(11)～式(13)，在阈值分布区间为[0,1]，M=4，N=4时，数值计算得到相关系数R随着乘性噪声强度D和加性噪声强度Q的变化情况。观察图2，系统中发生了阈上随机共振现象，即适量的噪声可以起到辅助信号传输的作用。在一定精度下，得到的最优噪声D=0.01，Q=0.44，在此种情况下，信号输出效果最佳。

图2 相关系数R随着乘性噪声强度D和加性噪声强度Q的变化(阈值分布区间为[0,1]，M=4，N=4)

图3和图4给出了在给定乘性噪声D(加性噪声Q)的情况下，相关系数R随着加性噪声Q(乘性噪声D)的变化情况。

设置阈值区间为[0,1]，阈值单元数N=4。在不同阈值单元输出元数下，图3(a)给出了当乘性噪声D=0.02，相关系数随着加性噪声Q的变化情况。图3(b)给出了加性噪声Q=0.02，相关系数随着乘性噪声D的变化情况，在图3中，相关系数的初始值和峰值随M值的增大而增加，且均发生了阈上随机共振现象。随着M的增大，阈值单元中的阈值相应减小，阈值输出元数对系统信息传输的提高能力已趋于饱和状态。

设置阈值区间为[0,1]，阈值输出元数M=4。在不同阈值单元个数下，图4(a)给出了当乘性噪声D=0.02，相关系数随着加性噪声Q的变化情况。图4(b)给出了加性噪声Q=0.02，相关系数随着乘性噪声D的变化情况。由图4，随着N的增大，相关系数的值也随之增大，且当N≥2时均发生了明显的阈上随机共振现象。这表明，在非零噪声情况下，增加阈值单元的个数能明显提高系统中信息传输的能力。

(a)乘性噪声D=0.02 (b)加性噪声Q=0.02

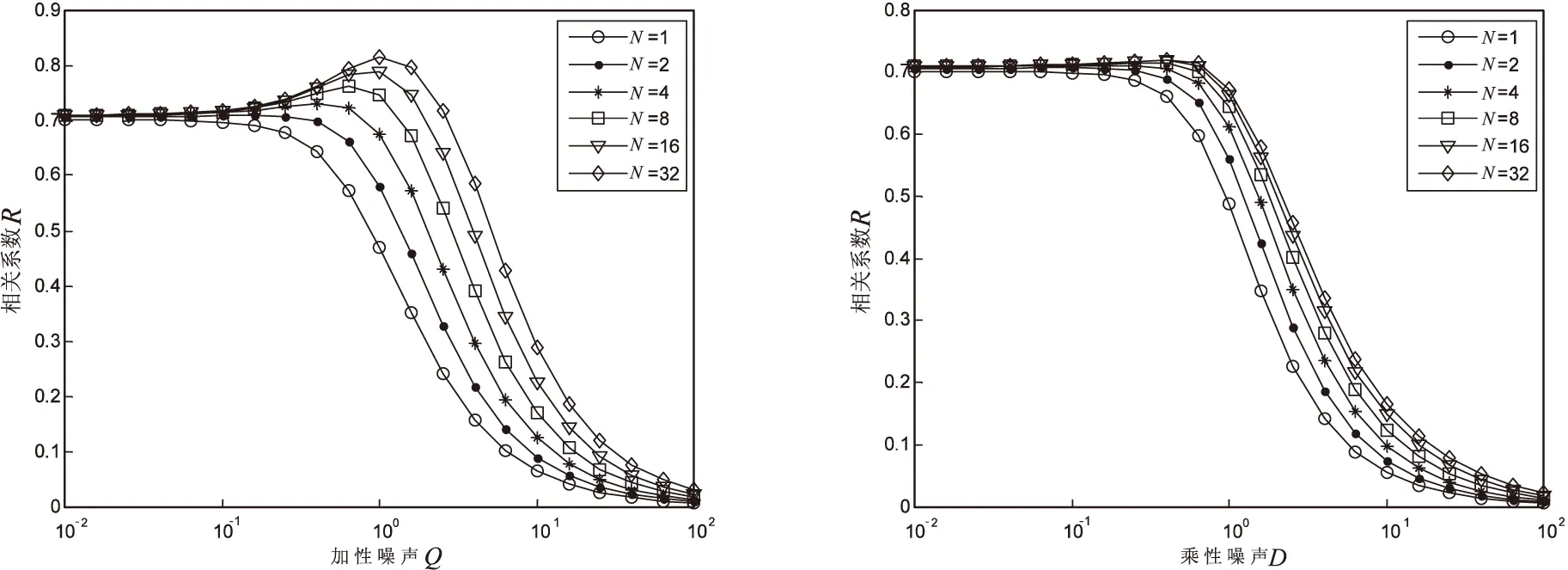
(a)乘性噪声D=0.02 (b)加性噪声Q=0.02

2 实际语音信号传输

选取了一个时长为2秒，采样频率为44 100 Hz的音频文件，如图5所示。

图5 语音信号时域图

该文将音频文件作为图1所示的多阈值系统的输入信号进行仿真。对于给定的语音输入信号x=(x1,x2,…,xl)以及系统输出信号y=(y1,y2,…,yl)，l是信号长度，输入信号x和输出信号y的平均值分别为：

(14)

输入输出的相关系数表达式如下：

(15)

通过仿真，图6和图7给出了在给定乘性噪声D(加性噪声Q)的情况下，相关系数R随着加性噪声Q(乘性噪声D)的变化情况。

(a)乘性噪声D=0.02 (b)加性噪声Q=0.02

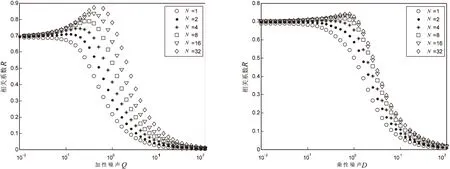
(a)乘性噪声D=0.02 (b)加性噪声Q=0.02

图6中，随着阈值输出元数M的增大，语音信号处理效果逐渐增强，进一步增大M，阈上随机共振功效逐渐趋于饱和。在图7中，当阈值单元个数N=1时，未发生阈上随机共振现象；当N≥2时，均发生了明显的阈上随机共振现象，即增加阈值单元数可以有效地改善系统中语言信号的传输。

3 结束语

从理论和实例两个方面探讨了利用阈上随机共振现象来改善语音信号的传输。在多阈值系统中，分别讨论了当输入信号为拉普拉斯信号和真实语音信号时，加性高斯噪声和乘性高斯噪声共同诱导的阈上随机共振现象。

结果表明，阈上随机共振功效可有效改善语音信号的传输效果，在最优噪声强度下，语音传输的效果达到最佳。此外，在一定的噪声强度下，增加阈值单元数和适当提高阈值输出元数均可以引发阈上随机共振现象，从而提高信息传输的效率。