基于类间相似方向数的二叉树支持向量机

王建建，何枫

（北京科技大学东凌经济管理学院，北京100083）

0 引言

支持向量机（SVM）是在统计学的理论上发展的一种新的机器学习方法[1]，起初是针对二分类问题而提出的，目前的研究重点是如何将其推广到多分类问题。目前解决该问题的方法主要分为两类：第一类是直接构造多分类问题的支持向量机模型，在一个最优化模型中求解多个分类面的参数，来“一次性”的实现求解多分类[2]。第二类是间接法，将多分类问题转化成二分类问题，即把多个不同的二分类器合并成一个多分类器。这类方法主要有四种：一对多方法（1-a-r）、一对一方法（1-a-1）、DDAG方法（决策导向非循环图法）和二叉树分类法。其中“一对多”方法[3]得到了广泛的应用，原因是其简单易实现，但也存在许多缺点，该方法会造成训练集不均匀，对小样本的类别识别精度低，并且存在不可识别区域；“一对一”方法[4]存在不可识别域，并且需要建立较多的支持向量机，对于很多类别的分类问题，导致训练时间加长，分类速度降低，且类别数的扩大引起预测函数增加，导致预测速度变慢；DDAG法采用了有向无环图的组合策略[5]，分类时虽不用经过所有的分类器，但增加了支持向量机的数目，随类别数的增加，训练时间也会很长，速度较低。

基于二叉树支持向量机[6]的分类方法避免上述问题，并解决了以下三个问题：（1）训练一个k分类问题，只要训练二分类向量机k-1个即可；（2）消除了以上方法存在的不可识别的区域；（3）与“一对多”的方法相比，训练时总的训练样本数目减少了很多。

采用二叉树的方法，首先，其结构较大的影响了整体的分类精度。不同结构的二叉树，由于分类顺序不同导致节点处的分类精度不同，进而影响最终的分类结果。其次，“误差累积”的影响，使得错误分类发生在越靠近根节点的地方，从而分类性能变差，因此在二叉树的结构产生过程中，应确保分离出最容易分离出来的一类。为解决这一问题，目前国内外研究二叉树生成的算法已经有很多[7-11]。本文在已有研究的基础上提出了一种类间相似方向数来作为生成偏二叉树支持向量机的准则。采用图示法和数值实验表明本文的方法具有一定的优越性。

1 基于类间相似方向数的二叉树多类分类算法

1.1 相关定义

定义1：中心向量[11]。一个类别的中心即为该类别所有训练样本向量的平均值，中心向量为：

为了研究三分类问题的分类顺序影响分类精度的问题，在文献[11]提出的类间相似方向的基础上，本文改进了类内和类间相似方向，再考虑到类间的距离，提出了类间相似方向数的相关定义如下：

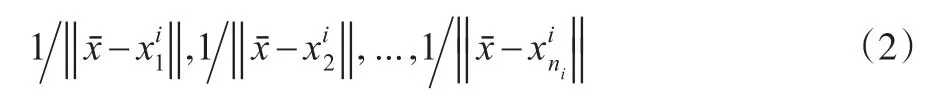
令类i的类内相似方向为：

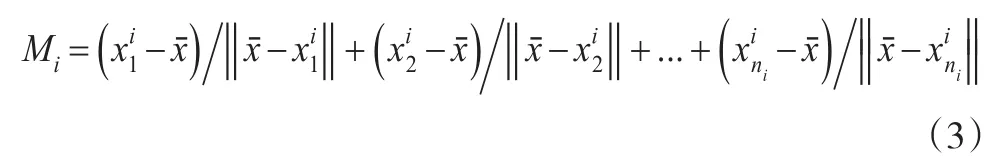
定义3：改进的类间相似方向。用Pi，j表示第i类训练样本集Si与第j类训练样本集Sj的相似方向，用di，j（dj，i）表示由类别i中心到类别j中心的向量（表示由类别j中心到类别i中心的向量），令：

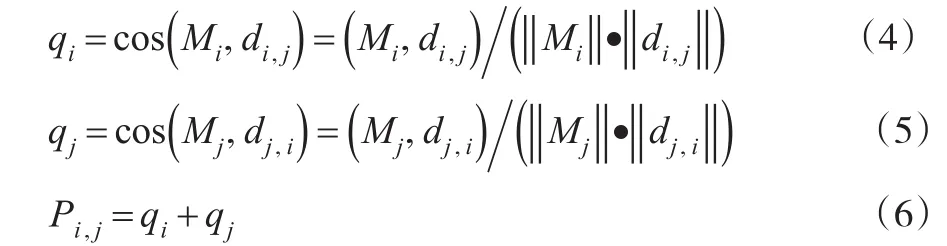
此时当Pi，j=qi+qj取得-2时，即qi，qj均取-1时，可使得i，j两类最不相似（即类间分离性最大），当Pi，j越小时也就是越容易分离,如图1所示。

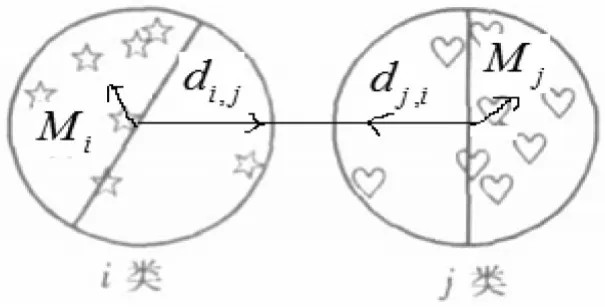
图1 改进的类间相似方向

定义4：类间相似方向数。定义类别i和类别j的类半径为ri，rj（即训练样本中距离中心点最远的点与中心之间的距离），定义类间相似方向数为：|di，j|为类中心距离，即向量di，j的长度，C＞0为合适的参数，一般取1即可，可根据样本点分布情况调整C的值，越大则越容易分离。

1.2 图示法比较本文方法与其他二叉树改进方法的优势

在判别两类之间的分离程度时，欧式距离是普遍使用的分离度，但距离并不能准确反映类的分布情况，如图2所示。

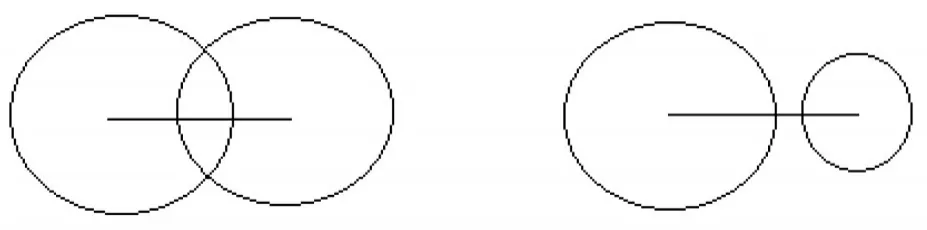
图2 中心距离相等的分离度的比较

图2中左右两图的两类别之间中心距离是相同的，显然右图两个类比左图的两个类更容易分开，所以这种情况下只依赖距离不能做出正确的判断。而按照本文定义的类间相似方向数=||di，j-C(qiri+qjrj)，则弥补了只依照距离的这方面的不足，能判断出右边的两个类更容易分离。

按照文献[11]提出的类间相似方向，不能正确的反映类与类间的分离程度，如图3所示。

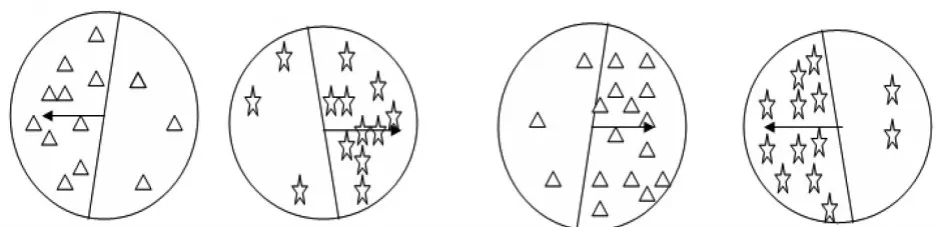
图3 左右两图表示两类间方向均相反的情况

图3中左图的两个类比右图的两个类更容易分开，但按照文献[11]的方法判断时把方向相反的即类间相似方向夹角余弦为-1时是最好分的，当分布情况类似为左图时，采用其方法可以很好地将两类分离出来，若分布为右图情况时，其类间相似方向夹角余弦也是-1，却不能采用这类方法将两类更好地分开。因此本文重新定义了新的类间相似方向数，避免了此种错误，按照本文的方法能判断出左边的两类更容易分离。

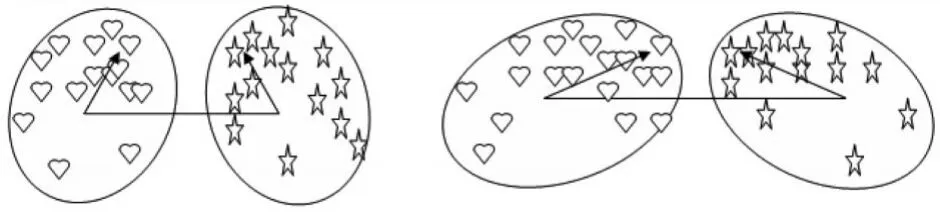
图4 左右两图表示两类间距离与类间相似方向的情况

比较图4中左右两图的情况可以发现，右图的类间距离虽然比左图的距离大，但是类与类之间的分布比较近，不容易分离；若只是按照距离的分离度来分类则应该先将右图的这类情况先分，但是按照距离来分类将不能更好地反映类之间的分布，当这种情况出现时，应按照距离并结合类间相似方向的方法来判断分类顺序，可避免这种错误的分类。

当上述图2至图4的情况出现时，单独靠距离或者类间相似方向不能较好地判别出正确的分类顺序，因此采用本文提出的方法，能更好地反映类之间的分布，确定出更加有效的分类顺序，从而有利于分类。通过以上图示之间比较可见，采用本文提出的类间相似方向数的二叉树支持向量机具有一定优势。

1.3 训练时间复杂度分析

引理1：训练时间复杂度的定律[12]

支持向量机求解的实质是二次规划问题，其训练时间随着样本数量的增大呈超线性关系，由如下能量守恒定律[12]描述：

式中，T为训练时间，γ为能量指数，m为样本的规模，c为比例常数。并且当采取SMO分析训练算法时，γ≈2。

假设训练样本集中共有m个样本点，有N类样本，每一类的数目相同，均为个，有引理1可得：

（1）一对多方法（1-a-r）需要构造N个分类器，每个及节点的样本分类数目为m，则整个分类器所需要的总的训练时间为：

其中当γ=2时，T1-a-r=cNm2。

（2）一对一方法（1-a-1）需要构造N(N-1) 2个分类器，每个及节点的样本分类数目为，则整个分类器所需要的总的训练时间为：

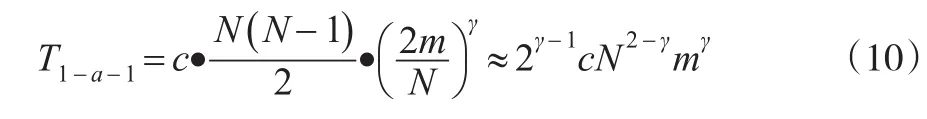
其中当γ=2时，T1-a-1=2cm2。DDAG方法进行训练分类时与一对一的方法相同，因此分类器所需要的训练时间与一对一方法（1-a-1）一样，即TDDAG=T1-a-1。

（3）本文二叉树方法需要构造N-1个分类器，每个及节点的样本分类数目为，其中i为分类的次数，则整个分类器所需要的总的训练时间为：

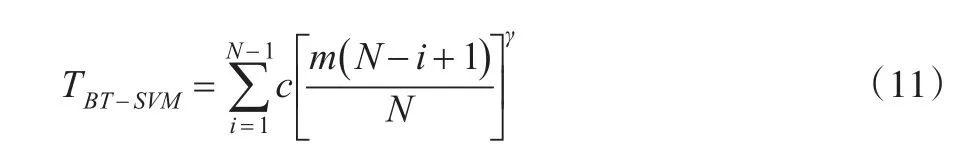
其中当γ=2时，TBT-SVM≈cNm23。

由以上分析可以得出，在分类的类别数目N较大时，本文二叉树算法的训练时间比一对一的时间要长，但是时间远小于一对多的情况。本文采用的实验数据类别为3类或4类，计算的时间也比一对一的要短。

1.4 以类间相似方向数作为生成二叉树支持向量机的多分类算法

步骤2：对于第i类，存在k-1个与其他各类的类间相似方向数，将这k-1个数按照从小到大的顺序排列起来，类似于第i类，计算(j=1，2，...，k，j≠i)按照由小到大的顺序进行排列为≤≤...≤。

步骤4：采用二分类的SVM算法建立二叉树各节点的最优超平面。根据类别标号的排序，从训练样本集中选第n1类样本为正类样本，其他剩余几类样本为负类样本，在根节点处建立第1个子分类器，并将第n1类样本删除，然后将第n2类样本作为正类样本在第二个节点处，其他为负类样本，构造第2个二值SVM子分类器，依次迭代之后，最终可得到基于二叉树的多类分类模型，如图5所示。

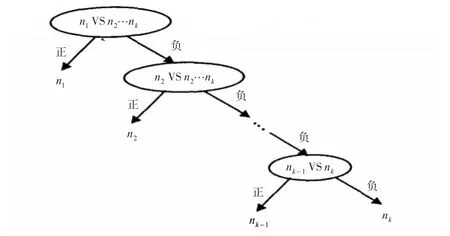
图5 生成二叉树的结构

步骤5：算法结束。

针对多分类问题，根据本算法由Matlab编程可以判别哪一类最先分出来能达到最优，给出合理的分类顺序，减少“误差积累”效应，使得最终的分类精度达到较高水平。

2 实验仿真与结果分析

2.1 人工模拟实验结果与分析

实验中所有训练样本与测试样本是在数据总量上随机选取，因此采用三倍交叉验证方法来进行实验，选取实验结果的平均值作为最终的实验结果。其中计算SVM的方法是采用工具箱OUS-SVM3.0，核函数则选取高斯径向基核函数，参数的选择固定。为验证本文提出的类间相似方向数生成二叉树结构的模型，随机生成一组模拟人工数据组，实验时其中的惩罚参数C采取1000，r取值为3。数据样本为600个，被分成三类，每类共有200个，如图6所示。（“×”记为1类，“+”记为2类，“○”记为3类）

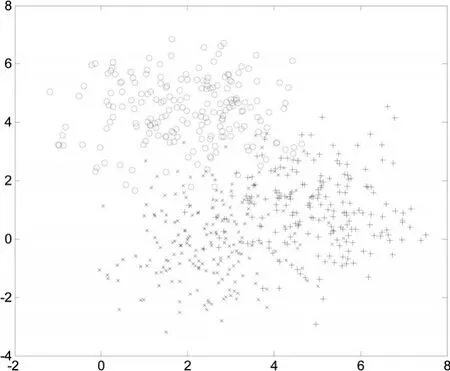
图6 人工模拟数据集

随机选出每类当中的一半作为训练样本，如图7所示。

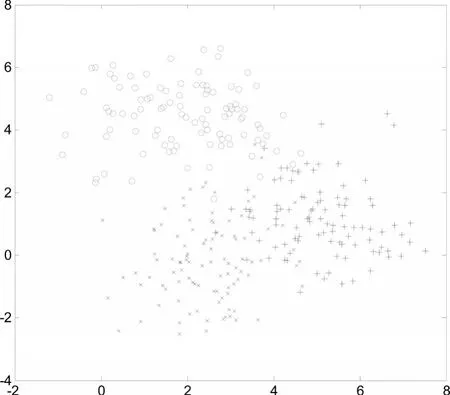
图7 人工模拟数据训练样本集

进而训练剩余两类会得到第二个分类模型，如下页图9所示。

将测试集代入第一个分类模型判断其属性，把不属于第三类的点再代入第二个分类模型判断其属性，经过这两个分类模型得到测试集的属性，并与原本数据的真实属性相比较，得到错分点的个数为48个，求得分类正确率84%。本文方法与一对一和一对多及其他二叉树的方法进行比较如表1所示的逼近精度及训练时间。

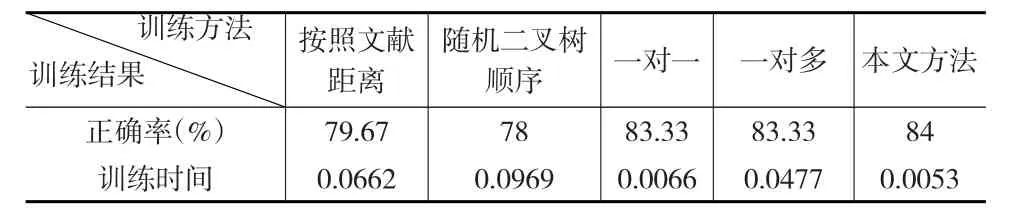
表1 对模拟数据集的各类方法的比较

图8 人工模拟数据训练样本集第一次分类

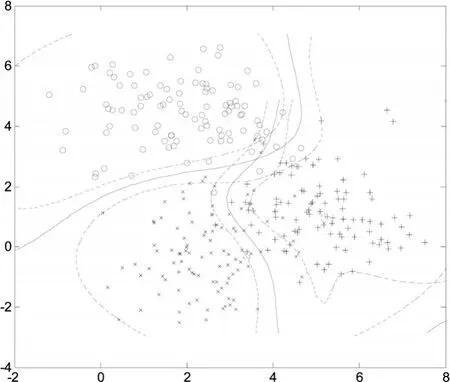
图9 人工模拟数据训练样本集第二次分类

2.2 UCI数据集上的实验结果与分析

本文所用的实验数据均来自UCI数据库，所有的样本个数、属性及类别均为已知的，所需要的实验数据如表2所示。其中iris（鸢尾花植物）的数据集共有150个样本，每个样本有4个特征属性，分别为：萼片长度和宽度，花瓣长度和宽度，数据被分成三类，分别为I:setosa,II:versicolor和III:virginica，每类样本是50个。Shuttle（航天飞机）的数据集有58000个样本，每个样本有9个属性，分别为时间（time）、拉德流（Rad Flow）、Fpv关闭（Fpv Close）、Fpv开放（Fpv Open）、高（High）、支路（Bypass）、Bpv关闭（Bpv Close）、Bpv开放（Bpv Open）、类别属性(Class Attribute)，由于其中的2、3、6、7类别个数较少，为了试验简便，因此实验时将这几类合并为一类，从而将样本分为了四类。Yeast（酵母）数据集有CYT,ERL,EXC,MEI,ME2，ME3,MIT,NUC,POX,UAX 10个类别,每个样本有8个属性，分为mcg(信号序列识别麦吉奥赫的方法)、gvh(信号序列识别冯海涅的方法)、alm（Alom预测得分）、mit（判别线非线粒体蛋白质的N端氨基酸含量得分）、erl(“HDEL”子串作为某信号保留在内质网腔的状态，二进制属性)、pox(定位末端的过氧化物酶体信号)、vac(评分判别分析的氨基酸含量的液泡和胞外蛋白)、nuc(核与非核蛋白核定位信号判别分析)，但是类别VAC,ERL,POX,EXC的个别属性未知且样本个数极少，因此把这些样本点删除，并将ME1,ME2,ME3这三类样本数较少的标记为一类，从而原始数据的1481个样本变为1394个样本点，由10类删减合并成4类问题。Auto_mpg（车辆MPG）数据集原始数据有406个样本点，删掉其中的个别属性未知的某些样本点，数据集变为392个，数据样本分成三类，每个样本点共有7个属性，分别为cylinders(汽缸)、displacement（排量）、horsepower（马力）、weight（体重）、acceleration（加速度）、model year（年份）、origin（产地）。Wine数据集共有178个数据点，分为1、2、3类,对应的样本点的个数分别为59、71、48个，每个样本点有13个属性特征,如alcohol（酒精）、malic acid（苹果酸）、ash（火山灰）、alcalinity of ash（灰分碱度）、magnesium（镁）等13个属性。

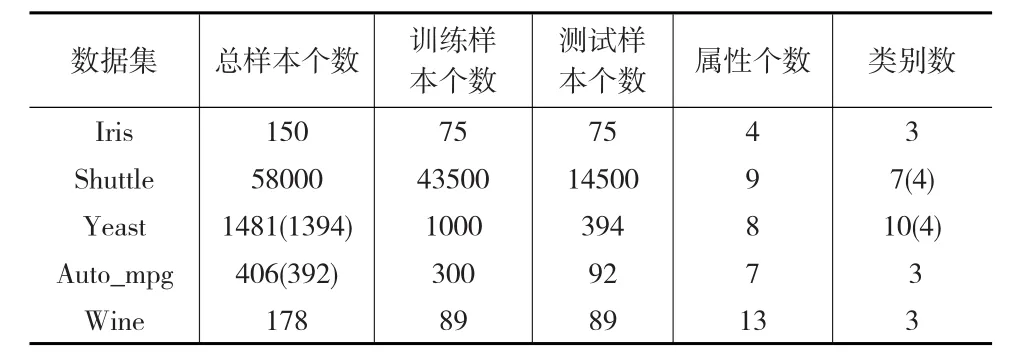
表2 实验所用的UCI数据集

数据样本进行实验时，为了避免数据中属性值范围大的比属性范围小的更具有影响力，故对所有样本数据进行归一化到[-1,1]上。实验时，采用RBF核函数，文中每一组实验所固定的最优参数(C，r)是经过网格搜索法来得到的推广精度最高的C与r参数。计算SVM的方法是采用工具箱OUS-SVM3.0，选用MATLAB工具编程来实现本文所有的算法，利用式（1）至式（7）给出分类顺序，通过SVM用Matlab编程计算可得数据实验结果如表3所示的逼近精度及训练时间。

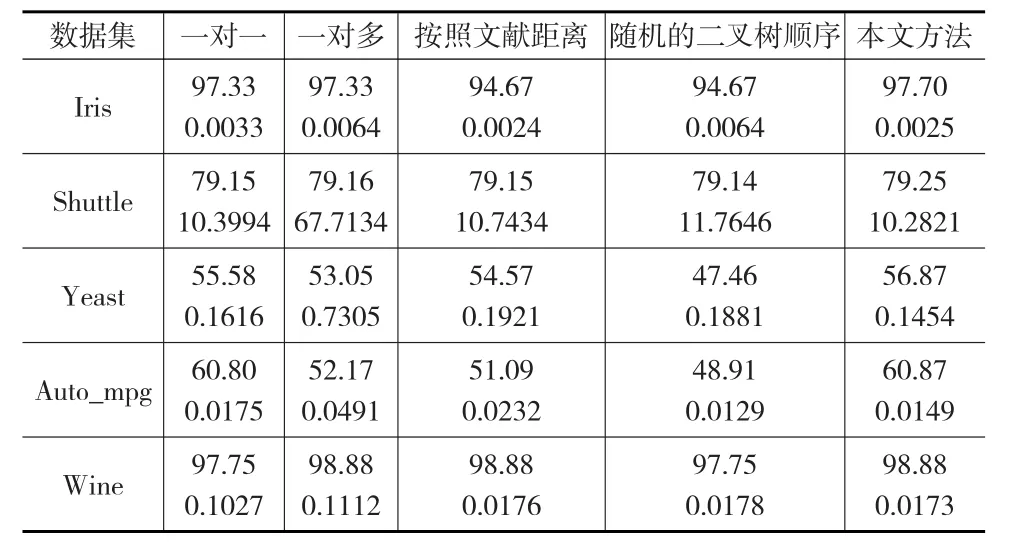
表3 对各个数据集的各类方法的比较

实验结果表明，由表2、表3结果分析可以得出采用本文方法与按距离生成二叉树的方法、一对一、一对多方法比较可知，本文方法得到的分类精度相对较高。与一对多方法相比，在分类精度接近的同时，明显分类速度要比一对多方法快出很多。因此进行多分类实验时，与其他方法相比，采用类间相似方向数来生成偏二叉树支持向量机能够使最容易分离出来的类最早分离出来，使得分类精度和分类效率都得到一定的提高。最后的数值实验验证了基于本文方法的二叉树支持向量分类机可以取得更优的分类精度。

3 结论

对于多分类当中的三分类问题，本文主要采用多分类的方法之一的二叉树支持向量机的方法研究，其分类效果与二叉树结构有很大关系。针对二叉树结构的分类顺序影响分类精度的问题，改进一种类间相似方向，并结合距离，提出了类间相似方向数作为二叉树结构生成的多分类方法，弥补了距离不能很好地反映类分离度的缺陷。采用本文提出的生成二叉树结构的方法进行数据实验分析，实验结果证明该方法具有较高的分类精度和分类效率。

[1] Vapnik V N.The Nature of Statistical Learning Theory[M]NewYork:Springer Verlag,1995.

[2] Madzarov G,Gjorgjevikj D,Chorbev I.A Multi-class SVM Classifier Utilizing Binary Decision Tree[J].Informatica,2009,33(2).

[3] Hill S I,Doucet A.A Framework for Kernel-Based Multi-Category Classification[J].Artif.Intell.Res.(JAIR),2007,(30).

[4] He X,Wang Z,Jin C,et al.A Simplified Multi-Class Support Vector Machine With Reduced Dual Optimization[J].Pattern Recognition Letters,2012,33(1).

[5] Martínez J,Iglesias C,Matías J M,et al.Solving the Slate Tile Classifi⁃cation Problem Using a DAGSVM Multiclassification Algorithm Based on SVM binary Classifiers With A One-Versus-All Approach[J].Applied Mathematics and Computation,2014,(230).

[6] Du P,Tan K,Xing X.A Novel Binary Tree Support Vector Machine for Hyperspectral Remote Sensing Image Classification[J].Optics Communications,2012,285(13).

[7] Cheong S,Oh S H,Lee S Y.Support Vector Machines With Binary Tree Architecture for Multi-Class Classification[J].Neural Informa⁃tion Processing-Letters and Reviews,2004,2(3).

[8] 孟媛媛，刘希玉.一种新的基于二叉树的SVM多类分类分法[J].计算机应用，2005,25（11）.

[9] 唐发明，王仲东，陈绵云.支持向量机多类分类算法研究[J].控制与决策，2005,20（7）.

[10] 唐发明，王仲东，陈绵云.一种新的二叉树多类支持向量机算法[J].计算机工程与应用，2005,20（7）.

[11] 汪洋,陈友利,刘军等.基于相似方向的二叉树支持向量机多类分类算[J].四川师范大学学报:自然科学版,2008,31(6).

[12] Platt J C,Cristianini N,Shawe-Taylor J.Large Margin DAGs for Multiclass Classification[C].nips,1999,(12).