异构多属性群决策的TOPSIS扩展方法

代文锋，齐春泽

（兰州财经大学信息工程学院，兰州730020）

0 引言

随着决策环境日趋复杂，决策往往需要多个决策者共同参与。然而，由于不同决策者在专业知识、决策经验以及对决策问题的认识等方面都会存在一定差异，因此他们选择的属性集，以及采用的信息表示模型也会有所不同。如果强行消除这种差异，一方面会导致信息丢失或失真，另一方面会大大削弱群决策的效用。在这种情况下，如何最大限度的保留所有决策者的偏好，充分发挥群决策的效用，进而做出更全面、客观的决策，相关决策方法的研究就显得尤为重要。

近年来，许多学者致力于多属性决策的研究，提出了一些决策方法。其中，Hwang等[1]提出的TOPSIS（Technique for Order Preference by Similarity to Ideal Solution）法以简单直观的特点成为目前最常用的决策方法之一。然而，传统的TOPSIS法存在一些不足：首先，传统TOPSIS仅适用于单人决策情景，无法解决群决策问题。针对这一不足，文献[2-5]将TOPSIS扩展到群决策环境；其次，传统TOPSIS法仅能处理属性值为精确值形式的决策问题。针对这一不足，文献[6-12]分别将TOPSIS扩展到区间数、模糊数、直觉模糊数以及犹豫模糊数等决策环境，但这些方法仅能处理某种特定形式的决策信息，但无法处理异构信息，而实际决策中的信息往往是异构的。随后，文献[13-16]提出了能够处理异构信息的TOPSIS扩展形式，但它们都需将异构信息转换为某种特定类型信息。

尽管上述方法解决了一些多属性决策问题，但它们仍存在一些不足。首先，除文献[13-16]外，其余文献均不能处理异构信息。文献[13-15]虽然可以处理异构信息，但需要进行信息类型转换，而转换会导致信息丢失或失真。其次，不是所有的方法都支持群决策。最后，上述方法均要求决策者采用相同的属性集，这不仅会导致信息丢失与失真，还在很大程度上削弱了群决策的效用。

本文在现有研究的基础上，针对上述方法的局限性，提出一种新的决策方法。该方法能够很好地解决具有多个属性集的异构多属性群决策问题。首先，将每个决策者给出的决策矩阵按照属性划分为若干相互独立的单元；其次，计算每个单元内各评价值与相应正、负理想解之间的距离，并按照属性权重及专家权重对其进行集结，从而得到不同方案与正、负理想方案之间的距离。最后，根据不同方案与理想方案的相对贴近度对方案进行排序。由于该方法将每个决策者都看作一个独立的实体，允许其根据自身的专业知识及决策经验构建合适的属性集，选择最擅长的信息表示模型，因此最大限度的保留了决策者的决策偏好，减少了信息丢失与失真现象，进而有助于得到更为合理的决策结果。

1 预备知识

1.1 区间数

定义1[17]：设a=[aL，aU]={x|aL≤x≤aU，aL，aU∈R}为实数轴上的一个闭区间，则a为一个区间数。aL和aU分别为a的下界与上界，m(a)和w(a)分别为a的中心数和宽度，m(a)=(aL+aU)/2，w(a)=(aU-aL)/2。

定义2：设a=[aL，aU]和b=[bL，bU]为两个区间数，其距离公式为：

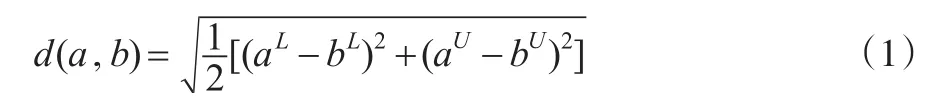
此外，如果m(a)＞m(b)，则a＞b；如果m(a)=m(b)，则a=b[18]。

1.2 梯形模糊数

定义4[19]：设=(a1a2a3a4)为实数域上的模糊数，如果其隶属函数为：

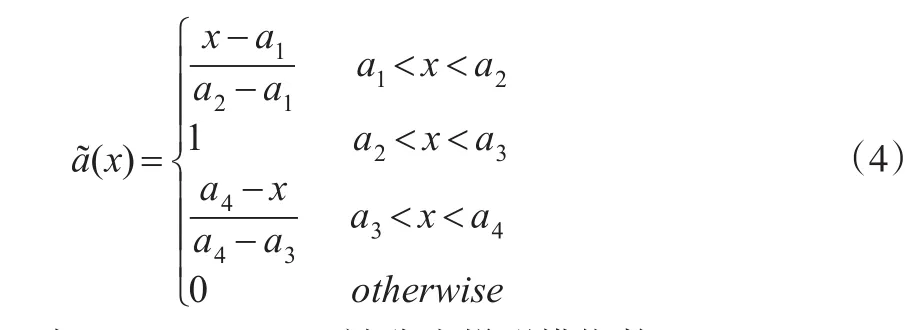
定义5[20]：设为两个梯形模糊数，则其距离公式为：

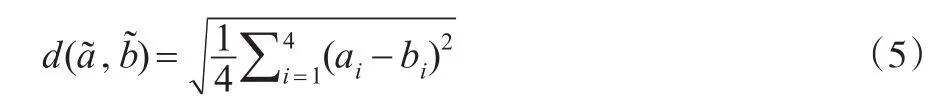
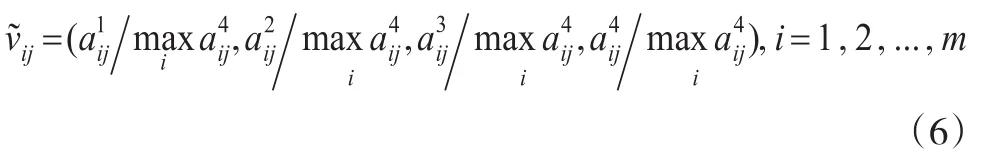
1.3直觉模糊数

定义8[21]：设X为一给定论域，则称P={|xiÎX}为X上的一个直觉模糊集，其中μP:X®[01]与vP:X®[01]分别表示P的隶属度与非隶属度函数，且对于任意xiÎX，都有0£μP(xi)+vP(xi)£1成立。πP(xi)为P中元素xi的犹豫度，πP(xi)=1-μP(xi)-vP(xi)。xi可记为(μP(xi)vP(xi))，1£i£m。为便于描述，如果X中仅有一个元素，则称P为直觉模糊数，记为P=(μPvP)。

2 基于扩展TOPSIS的异构多属性群决策方法

TOPSIS一经提出，便引起了许多学者的广泛关注，目前已出现了许多扩展形式。然而，如前所述，现有TOPSIS扩展形式虽解决了许多决策问题，但依然存在一些不足，因此很难满足复杂决策情景下的决策需求。现有TOPSIS扩展形式存在的主要问题有：（1）多数方法仅能处理具有单一信息类型的决策问题，而实际决策中的信息往往是异构的；（2）多数能够处理异构信息的决策方法仅适用于单人决策情景，而复杂问题决策往往是群体行为；（3）绝大多数群决策方法要求决策者须使用相同的属性集，因此容易引发信息丢失或失真现象；（4）现有方法都是在确定正、负理想解之前，将权重集结到决策矩阵，因此增加了计算的复杂性。

2.1问题描述

设某个决策问题的方案集为A={a1a2...am}，决策者集为E={e1e2...ed}，属性集为C={C1C2...Cd}，Ck={ck1ck2...cknk}为决策者ek采用的属性集，wk={wk1wk2...wknk}为属性集Ck中各属性的权重，nk为属性集Ck中属性的个数，k=12...d。表示决策者ek为方案ai的ckj属性给出的评价值，λ={λ1λ2...λd}表示决策者权重，决策者ek给出的决策矩阵可表示为：

2.2 决策过程

第一步：构建初始决策矩阵Dk(k=12...d)，将其按属性划分为若干单元，并根据每个单元的数据类型单独进行标准化，得到决策矩阵Sk=。

第二步：确定属性权重。

可采用最大偏差法确定属性权重，如果某个属性的偏差值越大，则分配给它的权重也应越大，反之则越小。具体计算公式如下：

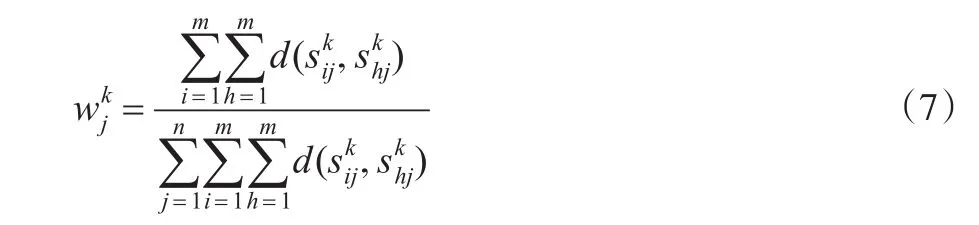
第四步：计算每个模块中各评价值与相应正、负理想解间的距离，集结所得结果，可得每个方案与正、负理想方案间的距离。

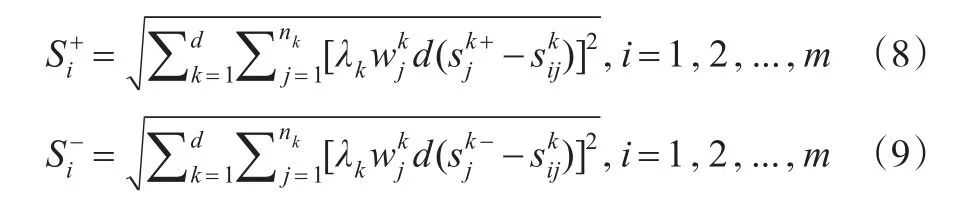
其中，λk表示决策者ek的权重，表示属性集Ck中属性ckj的权重。

第五步：计算每个方案与理想方案的贴近度Si，并据此对方案排序。

Si越大，方案Ai越好。

3 算例分析

下面通过两个算例证明本文所提方法的可行性与有效性。算例1的决策情景是决策者采用相同的属性集，算例2的决策情景是决策者采用不同的属性集。

3.1 算例1

为了证明所提方法的有效性，运用本文所提方法解决文献[16]中的决策问题。某招资银行拟从四个备选公司Ai(i=1，2，3，4)中选择前景最好的进行投资，特聘请3位专家el(l=1，2，3)组成评估小组，从经济效益c1，社会效益c2，环境污染和建设c3以及企业家再生产能力c4等方面对备选公司进行评价，其中，c1，c2和c4是效益型，c3是成本型。Dl(l=1，2，3)表示初始决策矩阵，如表1至表3所示，有关评价信息均来自文献[16]。

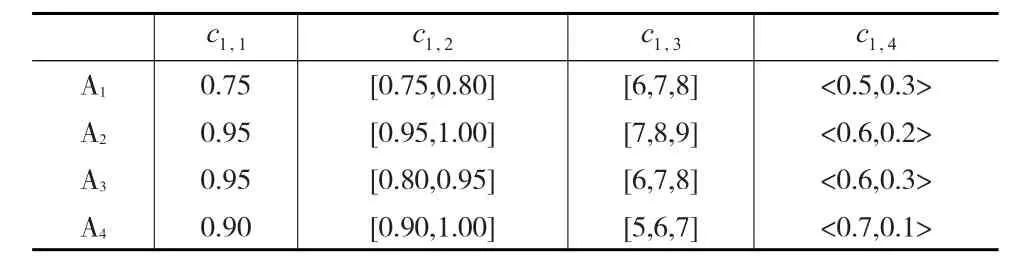
表1 决策矩阵D1

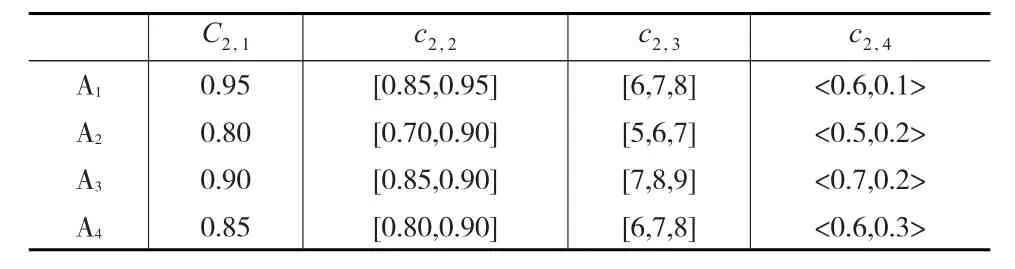
表2 决策矩阵D2

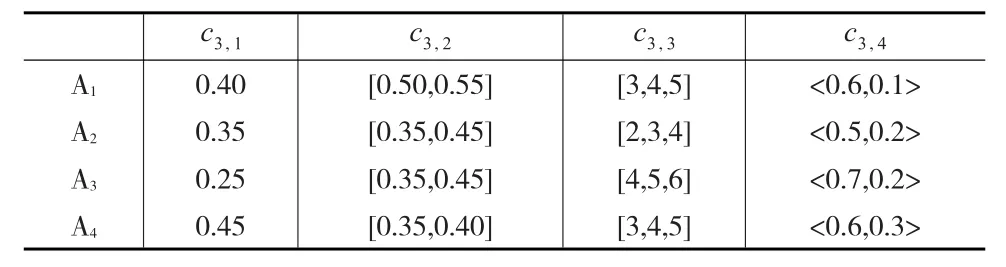
表3 决策矩阵D3

第一步：将初始决策矩阵按属性划分为若干单元，并据式（2）至式（6）分别进行标准化，得到决策矩阵Sl(l=1，2，3)，结果略。

第二步：确定每个单元的正、负理想解。

决策矩阵S1中各单元的正、负理想解分别为：=0.950，=[0.950，1.000]，=[0.556，0.667，0.778]，=＜0.700，0.100＞；=0.750，=[0.750，0.800]，=[0.778，0.889，1.000]，=＜0.500，0.300＞。

决策矩阵S2中各单元的正、负理想解分别为：=0.950，=[0.850，0.950]，=[0.556，0.667，0.778]，=＜0.700，0.200＞；=0.800，=[0.800，0.900]，=[0.778，0.889，1.000]=＜0.500，0.200＞。

决策矩阵S3中各模块的正、负理想解分别为：=0.450，=[0.500，0.550]，=[0.333，0.500，0.667]，=＜0.700，0.200＞；=0.250，=[0.350，0.400]=[0.667，0.833，1.000]，=＜0.500，0.200＞。

第三步：确定属性权重。

由文献[16]可知，决策者的权重为λ=(0.3，0.3，0.4)，3个决策者下每个属性的权重分别为：w1=(0.4，0.3，0.2，0.1)，w2=(0.4，0.2，0.3，0.1)，w3=(0.2，0.4，0.2，0.2)。

第四步：计算每个方案与正、负理想方案的距离。

由式（8）和式（9）可得各方案与正、负理想方案的距离分别为：=0.125，=0.098，=0.092，=0.123，=0.131，=0.086，=0.152，=0.121。

第五步：计算每个方案与理想方案的贴近度。

由式（10）可得各个方案与理想方案的贴近度为：S1=0.439，S2=0.572，S3=0.394，S4=0.442。因此可得A2≻A4≻A1≻A3，这与文献[16]得到的结果完全一样，说明本文所提方法是有效的。

3.2 算例2

某市拟对3个企业的综合实力进行比较评优，特聘请3名专家组成评价小组，每位专家根据自己的专业知识、决策经验以及对决策问题的理解分别给出属性集。由于专家意见未能达成一致，因此存在多个属性集。专家1给出的属性集为：经济效益c1，1，产品质量c1，2和售后服务c1，3；专家2给出的属性集为：经济效益c2，1，创新能力c2，2和企业文化c2，3；专家3给出的属性集为：经济效益c3，1，社会效益c3，2和环境污染c3，3。专家给出的初始决策矩阵如表4至表6所示，其中，c1，1，c2，1和c3，1的值为精确数，c1，2，c2，3和c3，2的值为梯形模糊数，其余属性的值为直觉模糊数。决策者给出专家的权重为λ=(0.3，0.3，0.4)。

表4 决策矩阵D1

表5 决策矩阵D2

表6 决策矩阵D3

第一步：将初始决策矩阵按属性划分为若干独立单元，并据式（2）至式（6）分别进行标准化，得到决策矩阵Sl(l=1，2，3)，如表7至表9所示。

表7 决策矩阵S1

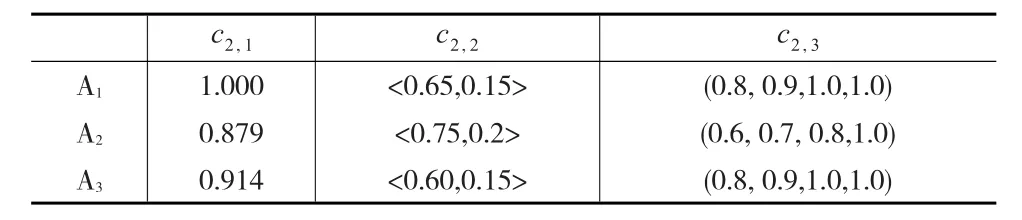
表8 决策矩阵S2

表9 决策矩阵S3

第二步：据式（7）确定属性权重，结果为：

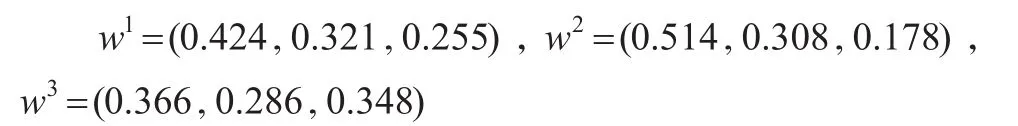
第四步：据式（8）和式（9）可得每个方案与正、负理想方案的距离。

第五步：据式（10）可得每个方案与理想方案的贴近度：S1=0.330，S2=0.593，S3=0.571。因此，可得A2≻A3≻A1，即企业A2的综合实力最强。

3.3 对比与分析

在算例1中，本文所提方法与文献[16]所提方法得到的结果完全一致，说明本文所提方法是可行的，也是有效的。在算例2中，由于不同专家采用的属性集不同，现有相关方法无法解决此类问题，而本文所提方法能够很好的解决，说明该方法能够处理更复杂的决策问题。

4 结论

本文针对具有多个属性集的异构多属性群决策问题，提出了一种新的决策方法。首先，将具有不同属性及信息类型的决策矩阵按属性划分为若干相互独立的单元，计算不同单元的评价值与相应正、负理想解间的距离。其次，根据专家权重及属性权重集结所得结果，得到不同方案与正、负理想方案间的距离。最后，根据不同方案与理想方案的相对贴近度对方案排序，并通过实例分析证明了所提方法的可行性与有效性。同现有相关方法相比，本文所提方法的主要优点为：（1）能够解决具有多个属性集的异构多属性群决策问题，弥补了现有相关文献的不足；（2）决策者可以根据自身的专业知识及决策经验构建合适的属性集，选择最擅长的信息表示模型，因此最大限度的保留了决策者的偏好，减少了信息丢失与失真现象。（3）现有方法将权重集结到决策矩阵后，才进行确定理想解、计算距离等一系列操作，而本文所提方法在计算方案与理想方案间距离时才引入权重，因此降低了计算的复杂性。将该方法扩展到动态决策环境是本文今后的研究重点。

[1] Hwang C L,Yoon K P.Multiple Attributes Decision Making:Methods and Applications[M].New York:Springer-Verlag,1981.

[2] Krohling R A,Campanharo V C.Fuzzy TOPSIS for Group Decision Making:A Case Study for Accidents With Oil Spill in the Sea[J].Ex⁃pert Syst.Appl,2011,38(4).

[3] Boran F E,Genç S.A Multi-criteria Intuitionistic Fuzzy Group Deci⁃sion Making for Supplier Selection With TOPSIS Method[J].Expert Syst.Appl,2009,36(8).

[4] Vahdani B,Mousavi S M.Group Decision Making Based on Novel Fuzzy Modified TOPSIS Method[J].Appl.Math.Model,2011,35(9).

[5] Li D F,et al.A Systematic Approach to Heterogeneous Multi-attribute Group Decision Making[J].Comput.Ind.Eng.2010,59(4).

[6] Dymova L,Sevastjanov P.A Direct Interval Extension of TOPSIS Method[J].Expert Syst.Appl.2013,40(12).

[7] Jahanshahloo G R,Lotfi F H.Extension of TOPSIS for Decision-mak⁃ing Problems With Interval Data:Interval Efficiency[J].Math.Com⁃put.Model.2009,(49).

[8] Yue Z.An Extended TOPSIS for Determining Weights of Decision Makers With Interval Numbers[J].Knowl.-Based Syst，2011,24(1).

[9] Lourenzutti R,Krohling R A.The Hellinger Distance in Multicriteria Decision Making:An Illustration to the TOPSIS and TODIM Methods[J].Expert Syst.Appl,2014,41(9).

[10] Chen C T,Extensions of the TOPSIS for Group Decision-making Un⁃der Fuzzy Environment[J].Fuzzy Sets Syst,2000,(1).

[11] Lee G,Jun K S,Chung E S.Robust Spatial Flood Vulnerability As⁃sessment for Han River Using Fuzzy TOPSIS With α-cut Level Set[J].Expert Syst,Appl.2014,41(2).

[12] Xu Z,Zhang X.Hesitant Fuzzy Multi-attribute Decision Making BasedonTOPSISWithIncompleteWeightInformation[J].Knowl.-Based Syst,2013,(52).

[13] Peng D,Gao C.TOPSIS-based Multi-criteria Group Decision Mak⁃ing Under Heterogeneous Information Setting[J].Adv.Mater.Res.2012.

[14] Wang J Q,Wang R Q.Hybrid Random Multi-criteria Decision-mak⁃ing Approach With Incomplete Certain Information[J].Control De⁃cis.Conf，2008.

[15] Espinilla M,de Andrés R.A 360-degree Performance Appraisal Model Dealing With Heterogeneous Information and Dependent Cri⁃teria[J].Inf.Sci.2013,(222).

[16] Lu J F.Hybrid Multi-attribute Group Decision Making Based on TOPSIS[J].Statistics and Decision Making,2015,(14).

[17] Tsaur R C.Decision Risk Analysis for an Interval TOPSIS Method[J].Appl.Math.Comput,2011,(218).

[18] Lourenzutti R,Krohling R A.A Modular Approach for the TOPSIS and TODIM Methods to Process Heterogeneous Types of Informa⁃tion,Technical Report[M].Espirito Santo：Graduate Program in Com⁃puter Science,Federal University,2014.

[19] Zadeh L A,Fuzzy Sets[J].Inf.Control,1965,(8).

[20] Dag-deviren M,Yavuz S,Kılınç N.Weapon Selection Using the AHP and TOPSIS Methods Under Fuzzy Environment[J].Expert Syst.Appl,2009,36(4).

[21] Atanassov K T.Intuitionistic Fuzzy Sets[J].Fuzzy Sets Syst,1986(20).