基于改进的三参数区间数距离熵的TOPSIS模型
王化中,强凤娇
(陕西科技大学管理学院,西安710021)
0 引言
在描述实际的多属性决策问题时,由于社会经济管理系统的复杂性及不确定性、决策者认识问题的有限性与判断的主观模糊性等因素制约,决策信息通常用某种不确定数的形式进行表达,随机数、模糊数、两参数区间数(简称区间数)、三参数区间数、四参数区间数、自然语言等形式经常被用于表征不确定数。其中,卜广志等[1]提出的三参数区间数在区间数上下限之间增加了灰数取值的最可能值,弥补了区间数“贫信息”的不足,因其更符合人类思维的灰色性与模糊性,能够更加细致地刻画不确定性信息,且覆盖信息更加客观全面,从而引起了广大学者的关注,基于三参数区间数的多属性决策问题也已经取得了一些可喜的研究成果[1-4]。
熵是信息论中系统稳定性程度与信息量大小的一种度量工具,熵越大表示系统稳定性越差,所含信息量越多。距离熵是王鹏飞[5]提出的用于度量两个灰数分布接近程度的新概念,两个灰数分布越接近,距离熵越大,反之亦然,所以用距离熵来度量两个灰数间的差异或接近程度是有效的。在多属性决策问题评价中,只要评价指标值中不出现负参数,基于距离熵的评价就可以不需要进行指标规范化处理便可实现多指标综合评价。规范化处理在一般的多属性决策方法应用中是必不可少的过程,虽然规范化处理可以通过消除不同指标单位、数量级及方向的不一致性等问题,使指标之间满足可加性,但无论采用何种规范化处理转换函数,转换后的各数据早己扭曲了原始数据之间的关系,因此以转换后数据运算得到的评价结果作为原始数据的评价结果具有一定的不合理性。特别对区间数、三参数区间数等反映的不确定性信息的规范化处理过程除过上述问题外,规范化处理过程更加繁琐,而且还可能带来经处理后数据灰度增加等新问题。王鹏飞[5]在提出距离熵的同时建立了正实数间及正区间数间的距离熵测度公式。王娜[4]将距离熵的概念推广到正三参数区间数,并构建了正三参数区间数的距离熵测度公式。但王娜建立的正三参数区间数距离熵公式中对三个参数等同对待,没有突出最可能值所表示的“重心”点在三参数区间数中的重要性。本文在考虑非负三参数区间数中三个参数概率分布的基础上,给出一种新型的非负三参数区间数距离熵测度公式,对其给定公式进行理论分析与证明,并基于新的三参数区间数距离熵建立了topsis模型,最后用实例验证了其评价模型的有效性。
1 三参数区间数距离熵测度公式存在的问题及改进
1.1 目前的三参数区间数距离熵测度公式及存在的不足
设有两个三参数区间数a(⊗)=[al,am,au](0<al≤am≤au)和b(⊗)=[bl,bm,bu](0<bl≤bm≤bu),王娜[4]给出的两个三参数区间数的距离熵测度公式见式(1)所示:
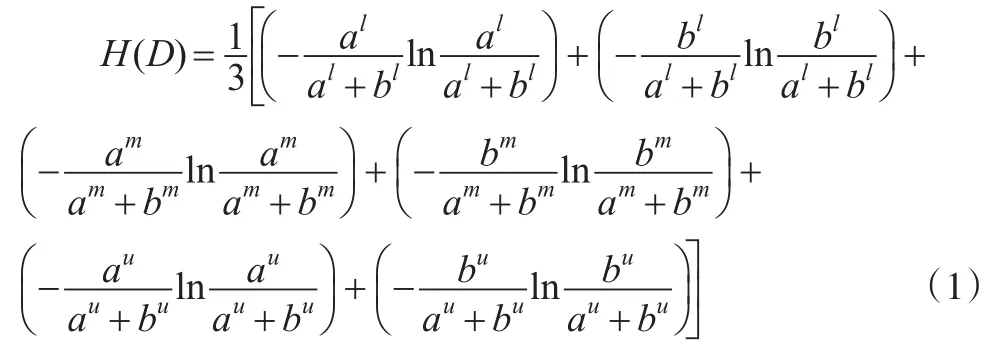
王娜[4]给出的两个三参数区间数距离熵测度公式对三参数区间数的上限、下限及最可能值三个参数同等对待,这不符合三个参数的相对概率分布,没有体现出最可能值相较上限、下限端点更加重要的特征,其本质是对三个参数各自距离熵进行算数平均来求得两个三参数区间数整体的距离熵。
1.2 三参数区间数距离熵测度公式的改进
朱建军等[6]认为三参数区间数中最可能值对应的分布概率p应该大于一个介于0~1之间的常量,且只有该常量达到一等程度时,才能称为最可能值。一般情况下,该常量取值大于等于60%,如果该常量取值过小,说明三参数区间数表示的决策信息过于分散。
本文对两个三参数区间数距离熵测度公式的改进思路是:以三个参数的相对概率分布为权重,对其三个参数的各自距离熵进行加权求和来得到两个三参数区间数整体的距离熵。因其三参数区间数中最可能值、上限、下限三个参数的相对概率分布值相差较大,其中最可能值在三个参数中的相对概率分布值远大于上限、下限两个参数的相对概率分布值,以三个参数的相对概率分布值为权重,对其三个参数的各自距离熵进行加权求和,体现了最可能值在整体三参数区间数距离熵计算中更加重要的作用,同时用上限、下限两个参数的概率分布值相对大小体现决策者在决策过程中不同的风险态度。
另外王鹏飞[5]、王娜[4]等给出的正实数、正区间数、正三参数区间数各自间的距离熵测度公式均使用自然对数(即取底数e=2.718281828)来求距离熵,以自然对数计算两个正数间的距离熵介于0与ln2=0.6931之间[1,4],当相对应的两个参数值相差较小时,以自然对数求得的距离熵灵敏度过低。故本文选择使用以2为底的对数来求距离熵,以提高不同参数对距离熵的灵敏度反映,且以2为底的对数计算得到的距离熵介于0和1之间(由文中经证明的定理1可知),也比较符合人们的判断习惯。当然也可以选择大于1且小于2的其他实数为底的对数,以进一步提高灵敏度,且以不同底数的对数分别计算得到的距离熵可以通过换底公式进行换算,所以采用不同底数计算的距离熵对两个正数的相对接近程度没有任何影响,仅仅是灵敏度有所差异。
定义1:对三参数区间数a(⊗)=[al,am,au](0<al≤am≤au)和b(⊗)=[bl,bm,bu](0<bl≤bm≤bu),假设两个三参数区间数各自的最可能值相较于其上限、下限两个端点参数而言,其分布概率为p(am)=p(bm)=α且α≥60%,两个三参数区间数的上限相较于最可能值、下限两个端点的分布概率为p(al)=p(bl)=β,两个三参数区间数的下限相较于最可能值、上限两个端点的分布概率为p(au)=p(bu)=γ,且β+γ=1-α≤40%。则本文给出两个三参数区间数a(⊗)和b(⊗)的距离熵H(D)ab(简写为H(D))测度公式见式(2)所示:
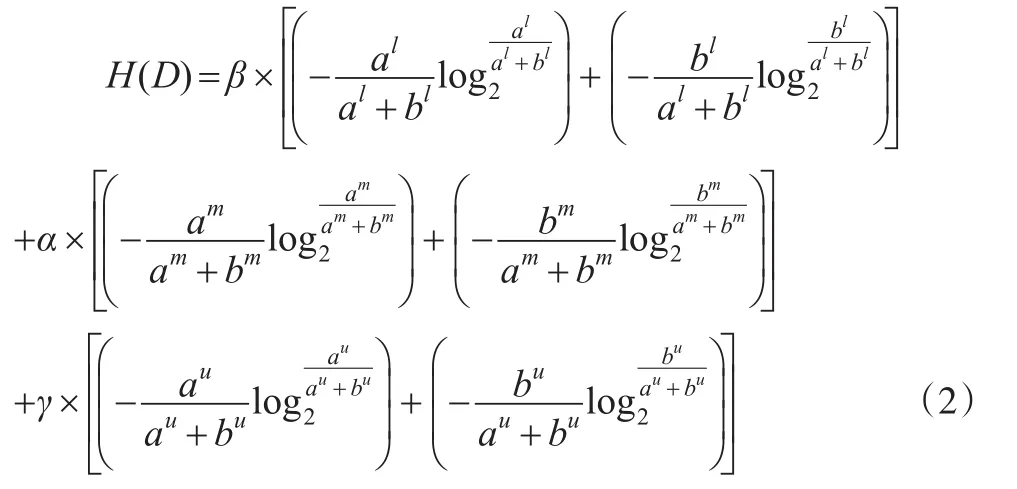
式(2)中,两个三参数区间数最可能值的概率α≥60%,表明距离熵H(D)受最可能值am、bm相对大小的影响大于上限、下限两个端点值相对大小的影响,体现了最可能值相较上限、下限端点更加重要的特征。β与γ的相对取值大小表示不同决策者的不同风险态度,当β>γ时,表示决策者较为慎重保守,尽量规避损失;当β<γ时,表示决策者敢于冒险,偏好收益;当β=γ时,表示决策者是风险中立者,对可能的损失与收益看重程度相等。
上述分析表明,两个三参数区间数的距离熵不仅与其各自三个参数的相对数值大小取值有关,还与其三个参数的相对概率分布有关。在实际决策问题中,三参数区间数的相对概率分布就是决策者信息把握程度与风险态度的充分反映。
定理1:设有两个三参数区间数a(⊗)=[al,am,au](0<al≤am≤au)和b(⊗)=[bl,bm,bu](0<bl≤bm≤bu),则:
(1)a(⊗)和b(⊗)的距离熵H(D)具有非负极值性,即满足0<H(D)≤1,特别当a(⊗)=b(⊗)(即al=bl,am=bm,au=bu)时,距离熵最大为mаxH(D)=1;
(2)a(⊗)和b(⊗)的距离熵H(D)ab与b(⊗)和a(⊗)的距离熵H(D)ba相等,即满足对称性。
证明:

同理,当am=bm时,H(d2)取最大值mаxH(d2)=1,当au=bu时,H(d3)取最大值mаxH(d3)=1;且同理H(d2)>0,H(d3)>0。
因此,当al=bl,am=bm,au=bu时,由0<β,γ<α<1且β+α+γ=1,两三参数区间数的距离熵最大为:mаxH(D)=β×mаxH(d1)+α×mаxH(d2)+γ×mаxH(d3)=1;且满足0<H(D)=β×H(d1)+α×H(d2)+γ×H(d3)≤1。
(2)因为三参数区间数距离熵的三个参数每一部分各自均满足对称性,因此关于三参数区间数距离熵整体对称性的证明较为简单(限于篇幅略去)。
定理2:两个三参数区间数a(⊗)和b(⊗)越接近其距离熵H(D)就越大,反之a(⊗)和b(⊗)越远离其距离熵H(D)就越小。
同理,am、bm数值相对距离越小(即ambm值越接近1)时,H(d2)越来越大;au、bu数值相对距离越小(即aubu值越接近1)时,H(d3)越来越大。
并由H(D)=β×H(d1)+α×H(d2)+γ×H(d3),且0<β,γ<α<1,β+α+γ=1,即可证a(⊗)和b(⊗)越接近其距离熵H(D)就越大,反之a(⊗)和b(⊗)越远离其距离熵H(D)就越小。
1.3 实数0与非负实数间的距离熵处理
只有两个正数(含正实数、正区间数、正三参数区间数等)才存在距离熵,因为负数及0的对数无意义。但现实决策问题中各指标取值可能存在非正数的情况,对其中的负参数,目前还无法直接计算距离熵,但对实数0与非负实数间的距离熵可以采用以下述两种方法予以处理。
第一种方法是将参数0用比其他所有参数值小很多的正数ε(如令ε=0.0001)来代替,然后再计算替代后的很小的正数ε=0.0001与其他非负实数间的距离熵,以此作为实数0与非负实数间距离熵的近似值(只要选取的正数ε足够小,所得到的近似值作为实数0与非负实数间的距离熵完全可以满足决策分析的需要)。
第二种方法是对实数0与非负实数的距离熵进行定义。
定义2:非负实数a、b(a,b≥0)在a=0,b>0(或b=0,a>0)时,a、b两个实数的距离熵为H(D)=在a=b=0时,a、b两个实数的距离熵为
将上述实数0与非负实数距离熵的处理方法一(或二)应用于式(2)的三参数区间数距离熵公式中,即可计算得到含0参数的非负三参数区间数与其他非负三参数区间数的距离熵。
2 基于三参数区间数距离熵的topsis多属性决策模型
2.1 问题的描述
设有n个备选方案Ai,m个属性指标Cj,方案Ai在指标Cj下的属性值以三参数区间数形式表示,记为xij(⊗)=[,,(i=1,2,…,n;j=1,2,…,m),属性指标Cj的权重为wj,且
2.2 三参数区间数距离熵的topsis多属性决策模型的决策步骤
(3)选择正负理想解。
对正指标,利用式(3)建立每个指标的正理想方案X+=,…,)和负理想方案X-=(,…,);对反指标,利用式(4)建立每个指标的正理想方案X+=,…,)和负理想方案X-=(,…)。
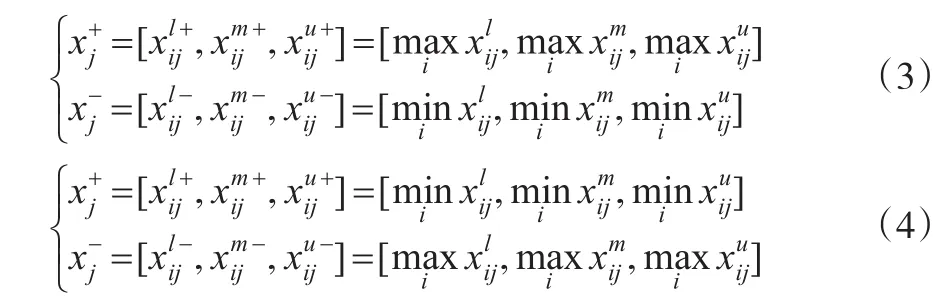

其中:
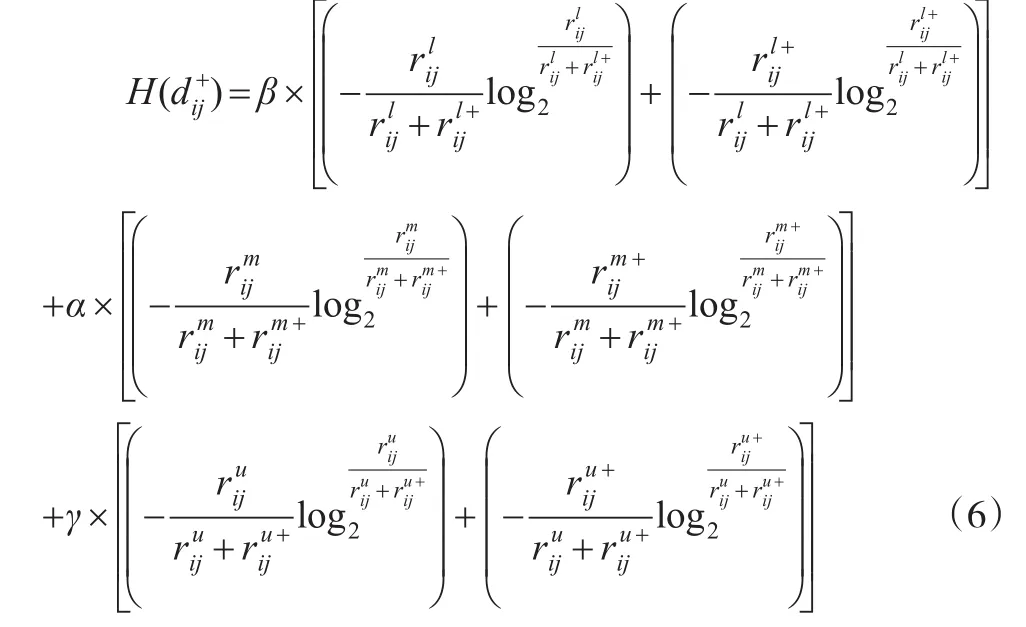

其中:
(6)计算各方案与正理想方案的贴近度Ci,并按照Ci的大小对方案从优到劣排序。

3 实例分析:企业信息化建设的软件项目方案选择
某企业欲进行信息化建设,现软件项目有5个方案(A1,A2,A3,A4,A5)可供选择,评价采用的5个指标为:成本C1(单位:万元)、收益C2(单位:万元)、功能C3(专家百分制打分)、研发周期C4(单位:月)、可维护性C5(专家百分制打分)。考虑到软件项目本身存在不确定性,不同专家的判断也存在差异,企业组建了一个8人评价专家组(包括企业相关部门成员及企业外聘专家)对5个方案进行评价与选择,为了更加细致地反映专家组的综合意见及项目指标的不确定性,对获取的每一方案不同指标的指标值经一定统计处理后,评价指标值均用三参数区间数表示,评价结果见表1所示。5个评价指标的权重用层次分析法确定,结果见表1所示。对5个方案的评选过程简介如下:
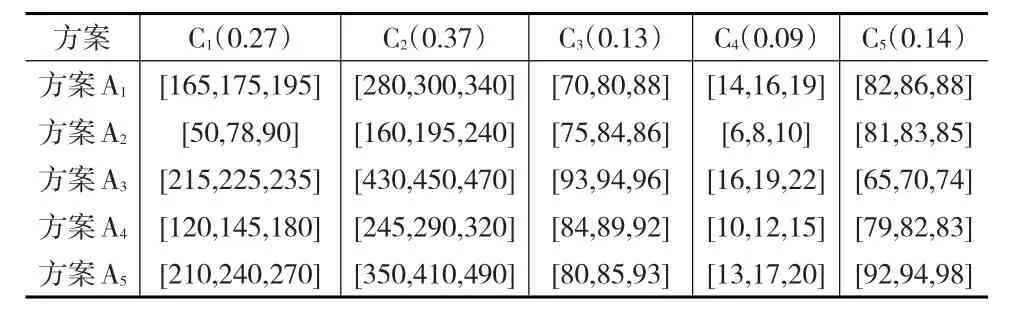
表1 软件项目评价结果
3.1 选择软件项目的正负理想解
收益C2、功能C3和可维护性C5属于正指标,成本C1和研发周期C4属于反指标,按照式(3)或式(4)建立的正负理想方案分别为:

3.2 分别计算各方案与正、负理想方案的距离熵和
先利用式(6)计算Ai方案与正理想方案X+关于j指标的距离熵H(),再利用式(5)计算Ai方案与正理想方案X+的距离熵,计算结果见表2所示。
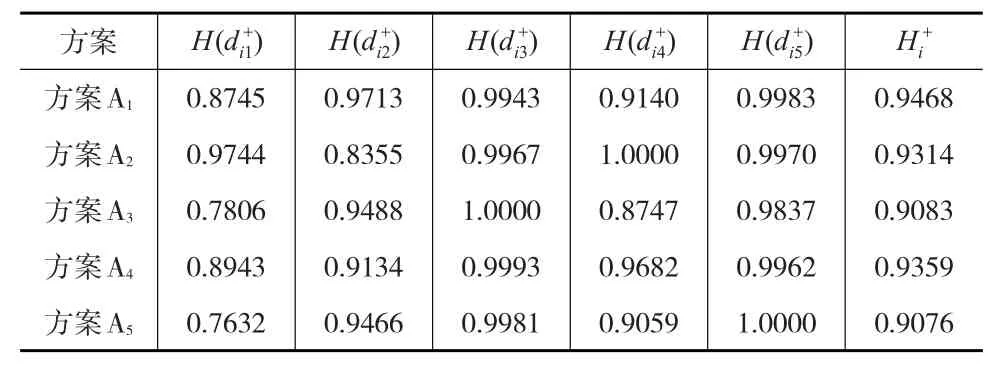
表2 各方案与正理想方案不同指标的距离熵表
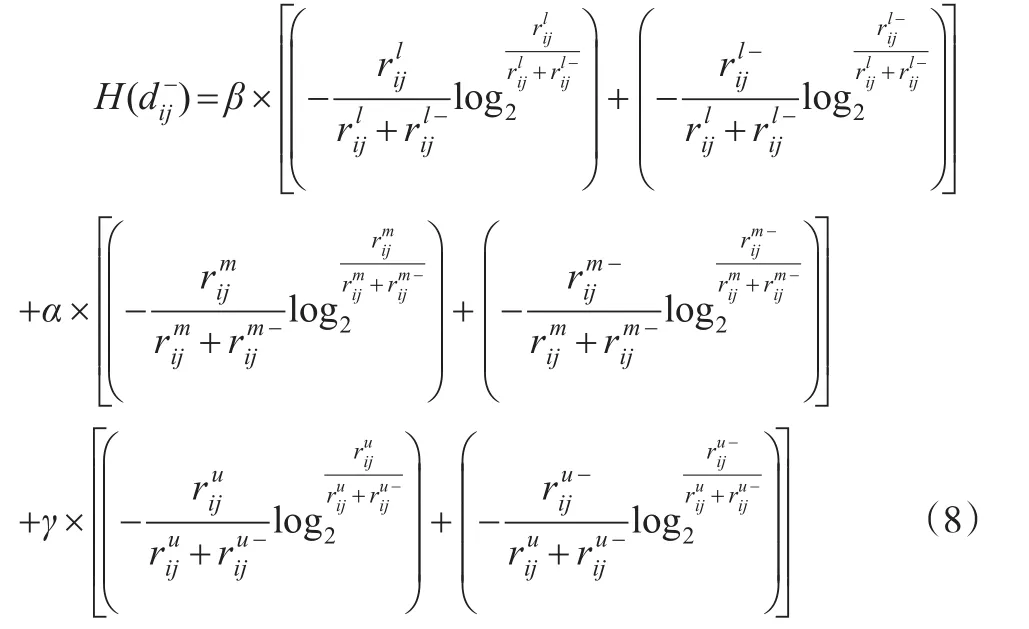
同理,先利用式(8)计算Ai方案与负理想方案关于j指标的距离熵H(),再利用式(7)计算Ai方案与负理想方案X-的距离熵,计算结果见表3所示。
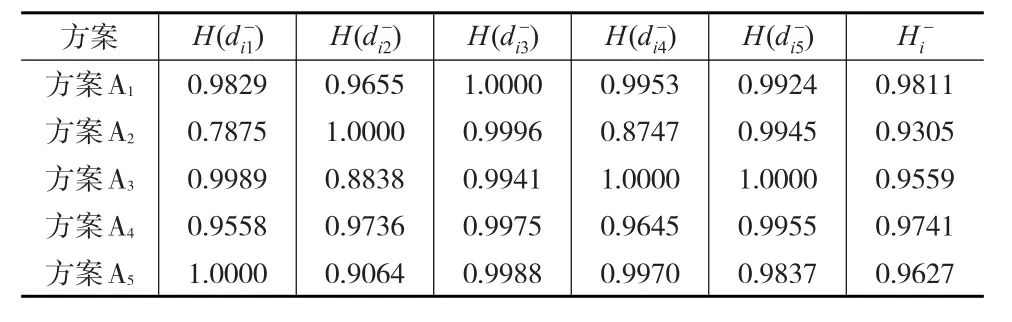
表3 各方案与负理想方案不同指标的距离熵表
3.3 计算各方案与正理想方案的贴近度Ci
依照贴近度大小,该企业信息化建设的软件项目最终选择贴近度最大的方案A2进行开发。
4 结论
针对现有的三参数区间数距离熵测度公式中对三个参数重要性同等对待的缺陷,本文结合三个参数在三参数区间数中的相对概率分布情况,提出了改进的三参数区间数距离熵测度公式算法,充分体现了最可能值相较上限、下限参数更加重要的特征,并从理论上证明了测度公式的有效性。在实际决策中对最可能值在三个参数中的相对重要性的概率及上限、下限参数的相对重要性概率,还必须结合决策信息的收集与整理背景以及决策者的风险态度来具体选择,从而使决策者的定性分析与方法的量化运算有机结合,保证决策结果更加符合实际决策需要。
对现实决策问题中各指标取值可能存在负参数的多属性决策问题,负参数不能直接用来计算距离熵,须将含有负参数值的指标经一定的转换变为非负参数指标,才能用来计算距离熵,但转换后数据同样存在指标规范化处理过程带来的问题,即转化后数据之间的关系与原始数据之间的关系存在偏差。因此对含有负参数指标的多属性决策问题能否采用距离熵的方法进行有效性优劣评判,以及如何评判的问题,还需在以后的研究中予以进一步分析与确认。
[1] 卜广志,张宇文.基于三参数区间数的灰色模糊综合评判[J].系统工程与电子技术,2001,(9).
[2] 罗党.三参数区间灰数信息下的决策方法[J].系统工程理论与实践,2009,(1).
[3] 王化中,强凤娇.基于三参数区间数标准化及排序算法改进的多属性决策模型[J].统计与决策,2016,(13).
[4] 王娜,胡丽平,李炳军.三参数区间灰数的距离熵模型及应用研究[J].河南农业大学学报,2014,(3).
[5] 王鹏飞.基于灰熵的不确定多属性决策问题研究[D].南京:南京航空航天大学硕士论文,2009.
[6] 朱建军,宋传平,刘思峰等.一类三端点区间数判断矩阵的一致性及权重研究[J].系统工程学报,2008,(1).

