电离层中性气体释放的早期试验效应研究∗

赵海生 徐朝辉 高敬帆2) 许正文 吴健 冯杰 徐彬薛昆 李辉 马征征

1)(中国电波传播研究所,电波环境特性及模化技术重点实验室,青岛 266107)

2)(西安电子科技大学物理与光电工程学院,西安 710071)

1 引 言

1959年先驱者II发射时,Booker[1]首次利用垂测仪观测到了电离层洞的存在,此后又多次观测到火箭发射时产生的电离层洞,尤其在1973年Skylab发射期间观测到了空前巨大的电离层空洞[2−4].Mendillo等[5,6]分析了电离层洞形成和快速消失的原因,认为是电离层中的氧离子(O+)与尾焰中氢气(H2)和水(H2O)分子进行快速的离子-原子交换反应,生成分子离子,随后迅速与电离层中的电子复合,造成电离层等离子体快速损耗.Mendillo等[7]深入研究了中性气体释放物在电离层中的动力学过程和释放物在电离层近真空环境中的膨胀、冷凝、碰撞加热和自由扩散等物理过程,建立了化学物质释放研究的理论基础.Anderson和Bernhardt[8]在考虑了真实的电离层化学反应速度后,利用模式研究了在赤道电离层释放H2后的电子损耗量化结果,先后建立了H2点源释放的受扰电离层演化模型.H2和H2O等释放物先与O+离子反应后产生相应的正离子,正离子再与电子进行复合反应耗空电子,与H2和H2O吸附电子原理相同的释放物还有二氧化碳(CO2)、氧气(O2)、二氧化氮(NO2)等.

六氟化硫(SF6)气体吸附电子的方式不同于H2和H2O,其直接与电子反应产生相应的负离子,因此SF6耗空电子的速度更快、效率更高.Paul和Bernhardt等对SF6气体释放开展了广泛而深入的研究,先后研究了释放物云团在不均匀大气中的运动过程[9,10];研究了电离层扰动的等离子体和流体不稳定性[11];研究了SF6在电离层中的化学反应和动力学过程,建立点源释放的仿真模型[12];研究了SF6释放产生气辉辐射增强的原理,提出了气辉辐射强度的计算方法[13].赵海生等[14]建立了基于SF6释放的面向试验场景的三维精细化效应仿真模型.

与中性气体吸附电子产生电离层洞的原理不同,碱金属、碱土金属等金属蒸气在电离层中通过光致电离产生高密度电子云团,被称为电子密度增强类化学物质.Hunton[15]研究了Ba的光致电离机制,以及Ba原子在电离层中的动力学过程.Koons和Rocdcr[16]从试验现象出发,研究了Ba电离层释放激发电离层电场和等离子体波的物理机制.Schunk和Szuszczewicz[17,18]首先采用一维物理模型系统研究了不同电离层背景条件下,释放电子密度增强类释放物形成的人工等离子体云的扩散和经典扫雪机效应.此后,随着理论研究的深入和计算技术的发展,开展了大量三维等离子体云物理建模研究[19−30],建立了更为精细的等离子体云模型,研究了释放物在电离层中的动力学过程,计算了释放物密度的时空分布.模型从连续性方程和动量方程出发,研究了背景中性风场力、惯性力、地磁场以及电离层电场对等离子体云运动过程的影响,仿真了等离子体云的演化过程.

电离层化学物质释放技术从生产至今已经开展了大量的理论和试验研究,也取得了丰硕的成果.但是,对电离层化学物质释放的早期试验效应,特别是中性气体释放的早期试验效应的研究很少.在电离层释放电子吸附类中性气体能够引起电离层电子密度耗空,在释放之后快速形成电离层洞;同时,由于释放中性气体的快速膨胀,挤压背景等离子体,在电离层洞的外边缘产生壳状电子密度增强结构,电离层洞和电子密度增强结构同时存在是释放早期试验效应的显著特征.本文研究了电离层中性气体释放的早期试验效应,建立了早期试验效应物理模型,仿真了释放早期电子密度的时空演化过程,同时采用射线追踪方法研究了释放后10 s和120 s不同频率信号在扰动区的传播效应.电离层化学物质释放对深入研究电离层动力学过程及耦合机制、研究电离层不稳定激发机制和过程、构建新的不稳定性理论体系具有重要的意义.

2 释放物在电离层中的膨胀过程

释放物的扩散过程满足连续性方程和动量方程.

连续方程为

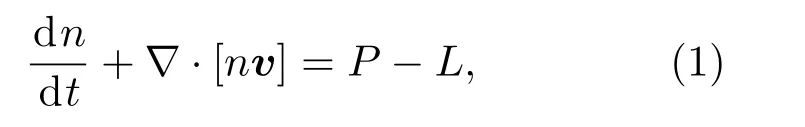
式中,n是释放气体密度,v是释放气体速度,P和L分别是化学产生和损失项.连续方程来源于在假设粒子流连续的情况下的玻尔兹曼方程.

释放物速度可通过动量方程得到:

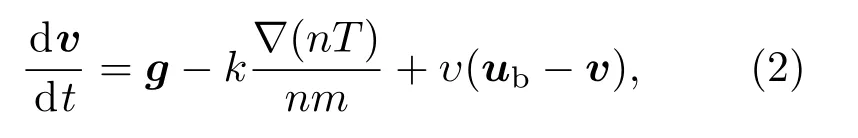
式中,g=−gˆaz是重力加速度,ˆaz是向上速度的单位矢量,T是气体温度,ub是背景大气风速,υ是释放物总和碰撞频率.由于释放物粒子自由运动周期远大于碰撞周期,加速度可以忽略,即dv/dt=0.那么,速度的表达式为

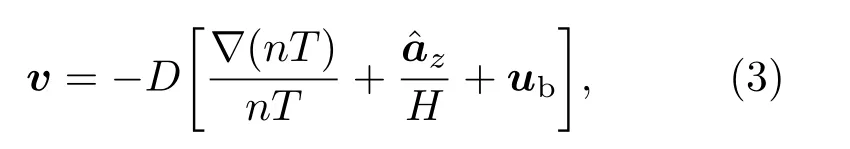
式中,D是扩散系数,H=kT/(mg)是释放气体云团标高.气体速度由两部分组成:密度和温度梯度产生的扩散速度,背景大气运动产生的飘移速度.

将(3)式代入(1)式得到一般扩散方程:

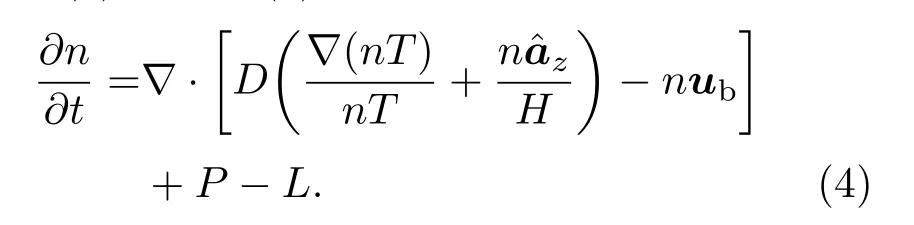
如果D和T是常量,忽略重力、大气运动、产生率和损失率,(4)式可归纳为简化的扩散方程.

在背景大气平面分层的假设下,忽略背景大气的运动、释放物分子的热扩散、释放物质的膨胀过程,释放物扩散方程可以表示为

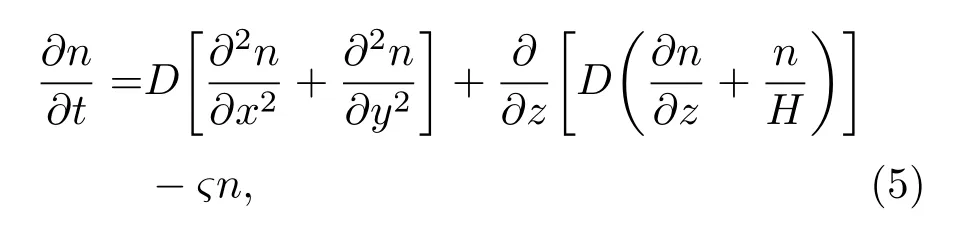
式中,ς是释放物反应损失系数.选取笛卡尔坐标系,以释放点为原点,z轴为垂直于地面的方向.假设大气参量服从指数分布,有D(z)=D0exp(z/Hb),其中D0为释放点(z=0)的扩散系数,Hb是背景大气标高.(5)式的最后一项表示注入气体与电离层的化学反应损耗.通过谱方法求解微分方程(5),可得到[10]

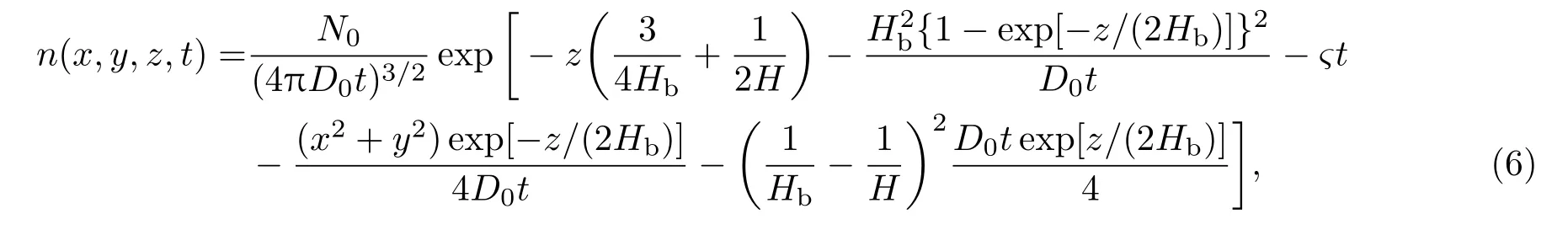
表达式(6)可用于计算自由扩散阶段任意时刻中性释放物密度分布.

3 早期释放效应数值模拟理论

在释放之初,释放物快速膨胀(约3000 m/s),膨胀速度大于背景大气声速(约600 m/s),在释放物云团的边界处形成了激波,波阵面附近背景气体因压缩而密度升高,电子密度也随之升高,形成电子密度聚集区.同时释放物与背景等离子体化学反应,形成电子密度空洞,随着释放物的膨胀,电离层洞随之扩大.之后释放物扩散速度逐渐降低到背景声速之下,激波消失,聚集区的电子密度逐渐恢复到背景水平;而形成的电离层洞继续扩大,洞的深度逐渐减小.以下从等离子体连续性方程和动量方程出发,推导电子密度增强区和电离层洞的形成及演化理论.

释放区等离子体连续性方程可以表示为

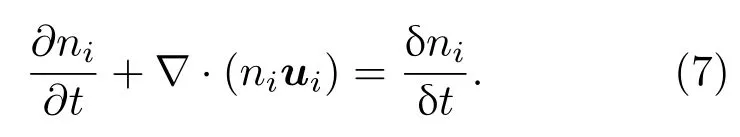
等离子体动量方程可以表示为

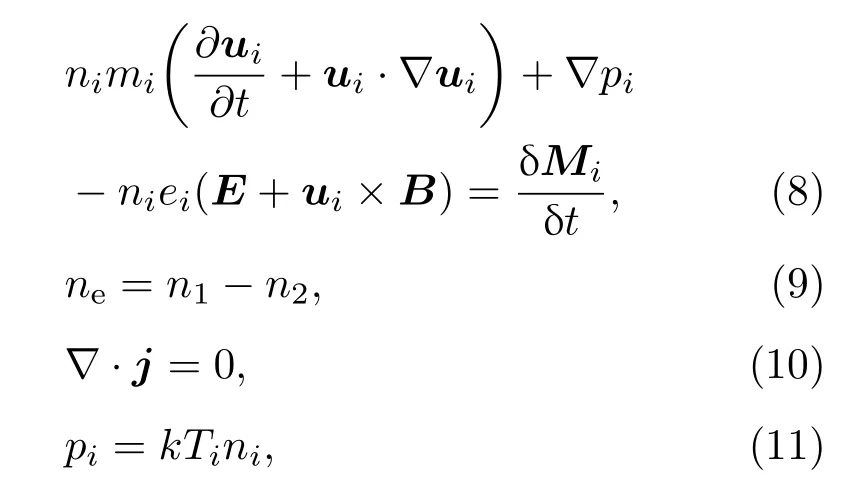
式中,i=1代表背景电离层正离子O+,i=2代表释放物云的负离子e为电子;ni,ui,mi,ei,pi分别代表密度、飘移速度、质量、电量和压强;E,B,j分别代表电场、磁场和总电流密度;为基于点源释放的密度变化,为基于点源释放的动量变化.

对于背景电离层O+,假设在释放之初,其密度不随时间变化对于释放物负离子其密度变化可以表示为其中,σ为产生率,ns为释放物密度.

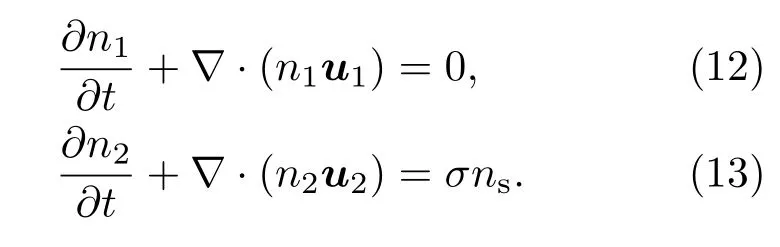
对于O+离子,其动量变化可以表示为

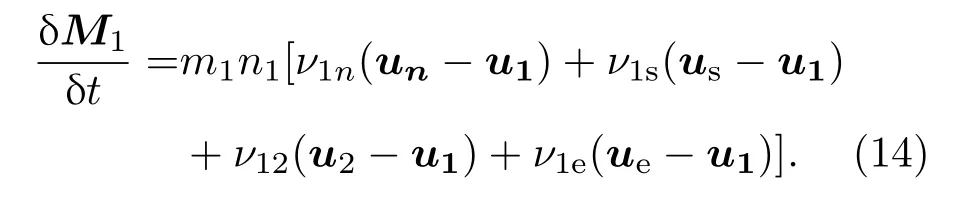
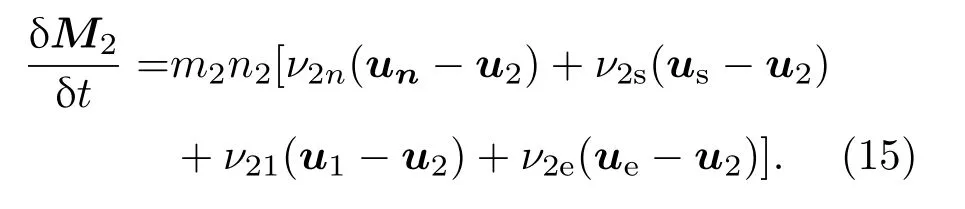
由于地磁场对带电离子的控制作用,不同带电离子垂直于磁场方向的速度差很小,因此相关的碰撞项可以忽略不计,但是沿磁场方向的碰撞项不能忽略.忽略带电离子的惯性,假设地磁场恒定,那么可以得到不同离子的漂移速度,表达式如下:

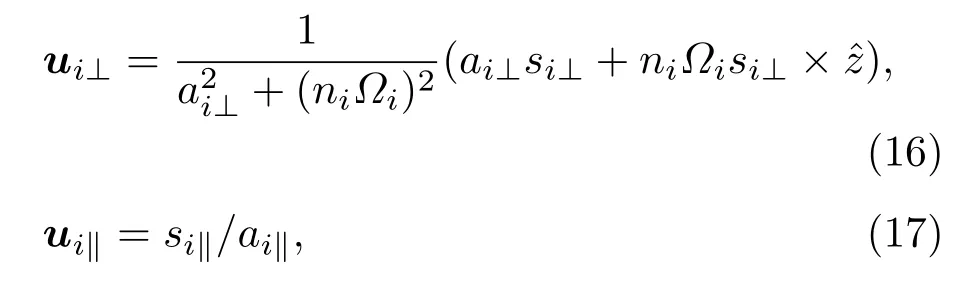
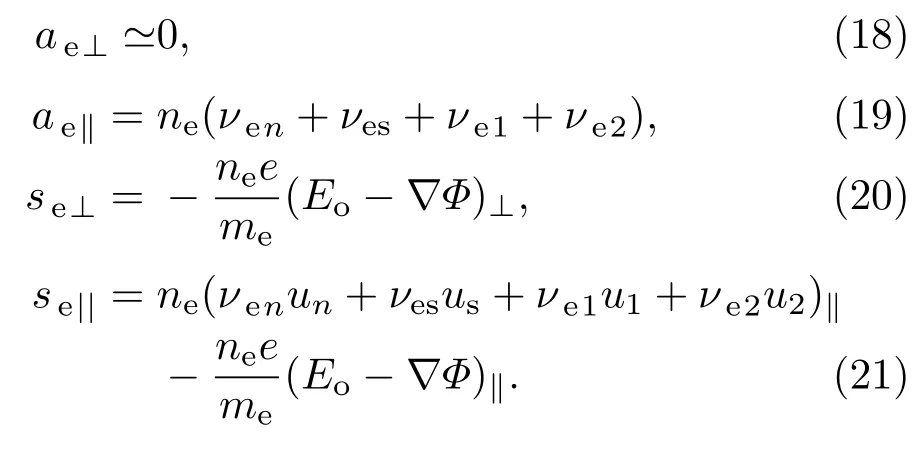
对于离子O+,a1⊥,a1‖,s1⊥,s1||分别定义为:

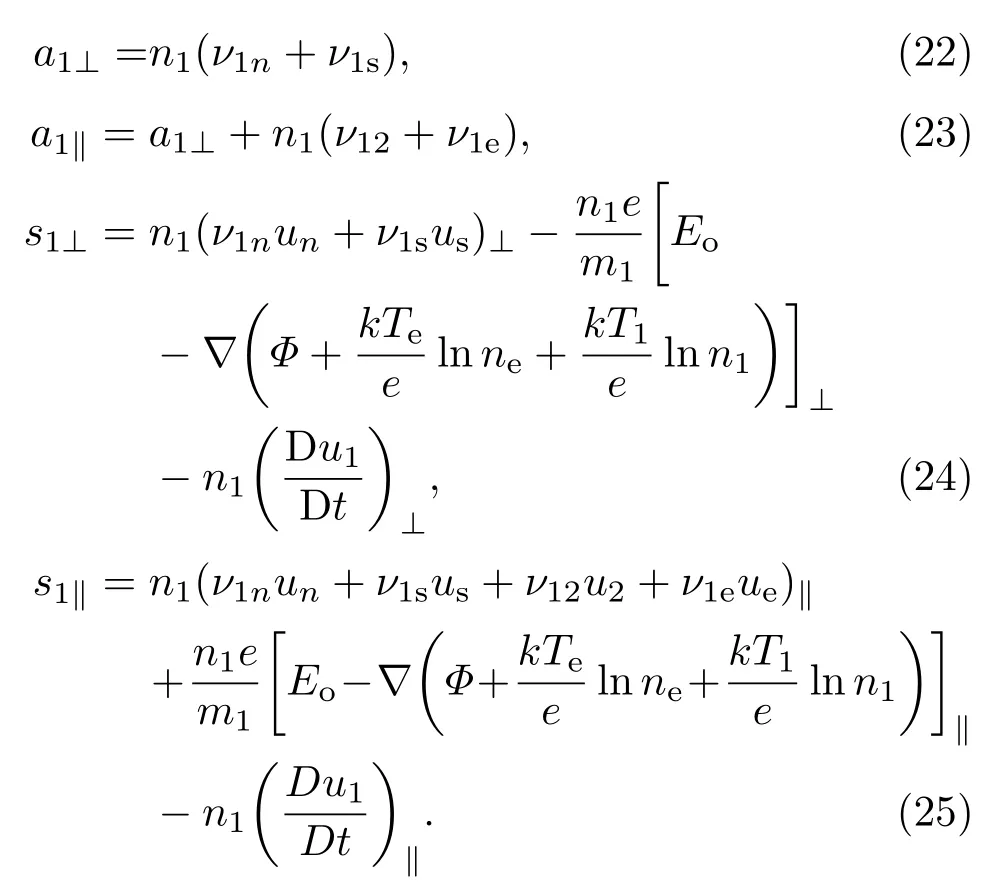
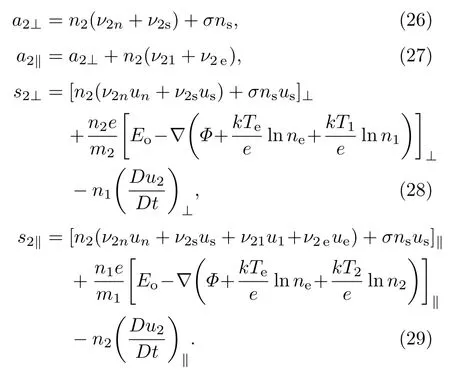
在(20)—(29)式中引进了电势Φ,其定义为Φ=ϕ−(kTe/e)ln(ne),那么电场可以表示为

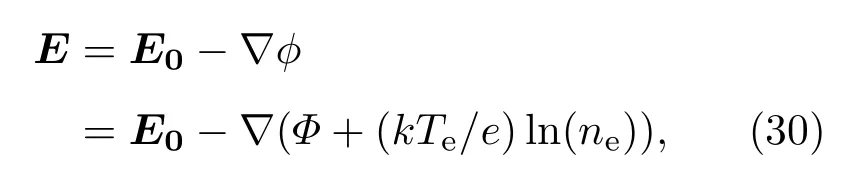
式中,E0为背景电场.假设在整个计算过程中E0保持恒定,可以得到以下关于Φ的方程:

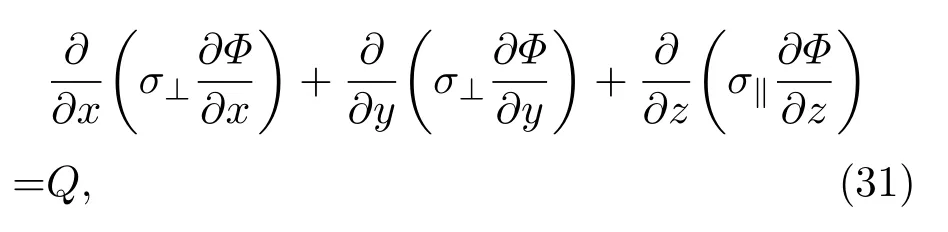
式中,σ⊥为Pederson电导率,σ‖为平行电导率,Q为电荷总量.

通过求解(31)式能够得到释放区的电势分布,从而求得释放区电场分布.通过(16)式求得任意离子的飘移速度分布,将飘移速度代入连续性方程(7),可以求得任意时刻电子密度分布.

4 数值模拟

根据第3节理论推导结果,本文通过虚构的试验场景(试验参数如表1所列),数值模拟了释放早期,电离层洞的形成以及释放物快速膨胀挤压背景等离子体,引起背景电子密度升高的演化过程.根据释放参数和SF6在电离层中的物理化学过程,通过求解释放物扩散过程和等离子体扩散方程,建立SF6释放的效应仿真模型,模型算法设计流程如图1所示.

效应仿真流程按照以下5个步骤进行:

1)根据试验具体情况进行释放参数设置,包括释放参数和火箭飞行参数,同时,根据释放物膨胀和化学反应过程,计算得到初始时刻空间电荷分布;

2)将空间电荷分布代入等离子体泊松方程,求解得到释放区域空间电场分布;

3)依据计算得到的空间电场分布、国际参考磁场模型、国际参考电离层模型IRI2012、标准大气模型,代入等离子体动量方程,求解等离子体飘移速度;

4)根据等离子体飘移速度代入等离子体连续性方程求解得到等离子体密度分布(包括正负离子和电子);

5)将计算得到的等离子体密度分布代入步骤3),重复执行步骤2)—4),计算得到任意时刻电子密度分布.

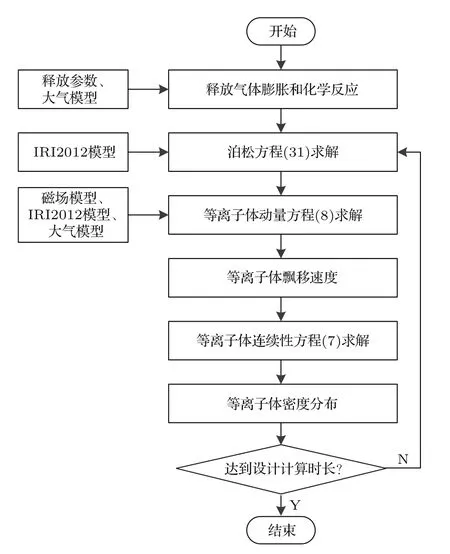
图1 电离层中性气体释放的早期试验效应仿真流程图Fig.1.The simulation fl owchart of the early time effects produced by neutral gas ionospheric chemical release.

为了验证效应仿真模型,本文采用虚拟试验场景开展了数值模拟研究,仿真参数设置如表1所列,试验时间201509301800LT代表当地时间2015年9月30日18:00.

图2描述了在300 km高度释放40 kg中性气体SF6,释放后0—120 s释放物密度分布的演化过程.在释放之初的2 min内释放物密度逐渐降低,从释放后1 s的最大密度2.3×109cm−3快速下降到释放后120 s的3.4×105cm−3,释放物分布范围快速增加,释放后5 s释放物分布范围为直径约10 km的球体,释放后120 s释放物分布直径达80 km以上.释放物密度降低主要取决于释放物快速膨胀体积增加,另外,释放物与背景电子化学反应产生相应的负离子,也造成释放物密度下降.

图3描述了在300 km高度释放40 kg中性气体SF6,释放后0—120 s扰动区域电子密度分布的演化过程.

从仿真结果可以看出,在释放之初由于释放物膨胀速度远大于背景声速,在释放物边界处形成了壳状电子密度聚集区,随后膨胀速度逐渐降低,边界处电子密度逐渐恢复到背景水平.释放后1 s释放物边界处的最大电子密度达2.46×106cm−3,约为背景电子密度的2.8倍,随后电子密度逐渐降低;释放后30 s,边界处的最大电子密度约1.58×106cm−3,约为背景电子密度的1.7倍.释放后120 s,边界处的最大电子密度约1.12×106cm−3,约为背景电子密度的1.2倍.整个电子密度聚集过程持续时间大约120 s,之后聚集区电子密度恢复到背景水平.在释放后2 min内,电离层洞的尺度逐渐增加,释放后5 s释放物分布范围为直径约10 km的球体,释放后120 s释放物分布直径达70 km以上,同时电离层洞的耗空深度缓慢降低,释放后1 s电离层洞100%耗空,到释放后120 s电离层洞耗空深度约为95%.

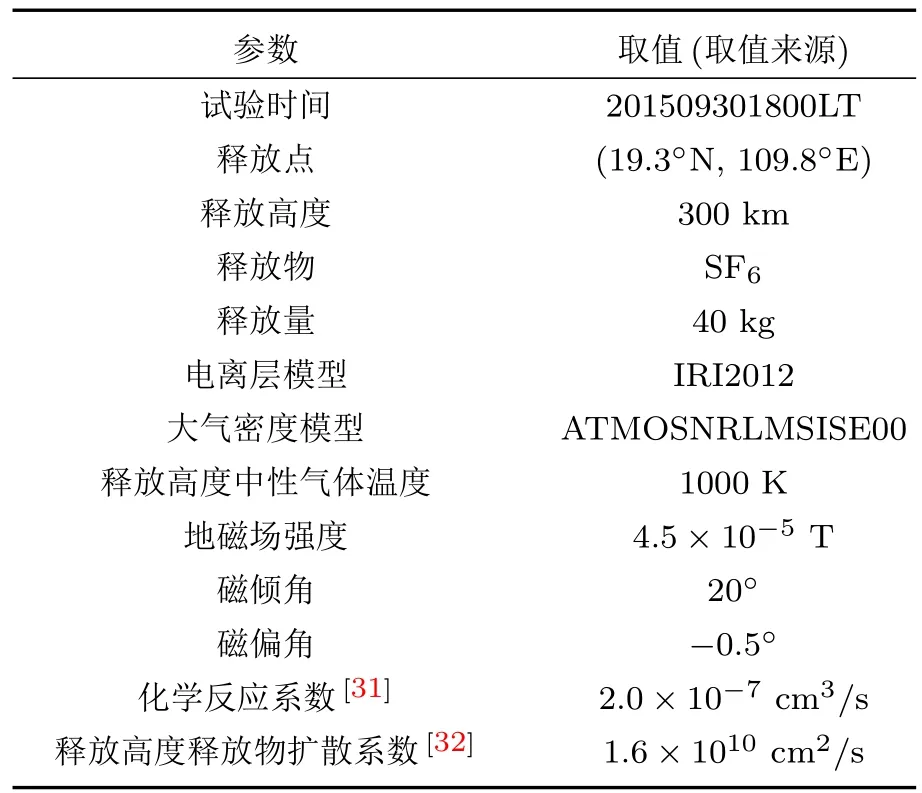
表1 主要仿真参数Table 1.Parameters for the simulation.

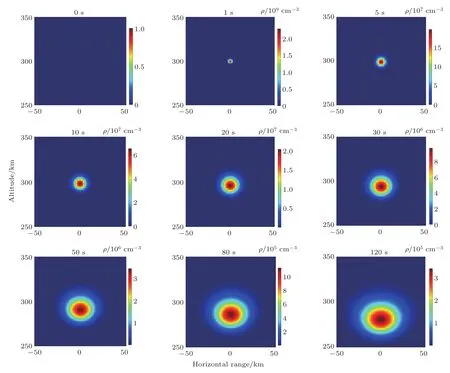
图2 释放物密度分布随时间的变化Fig.2.The distribution of release density varies with time.

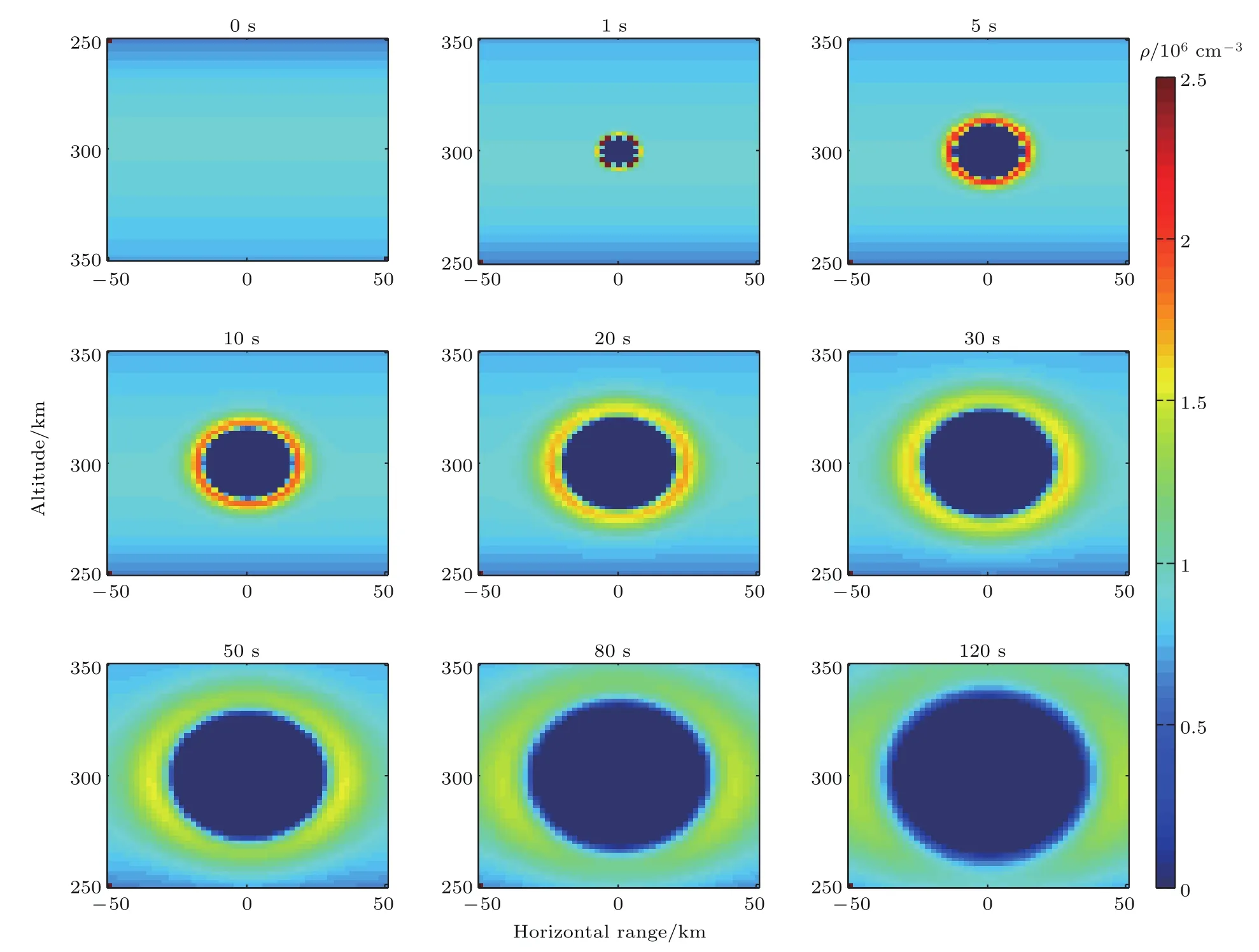
图3 释放早期释放区电子密度演化过程Fig.3.The electron density evolution process in release zone in the early time.

基于仿真得到的释放初期扰动效应的演化过程,采用射线追踪方法研究了电波信号在扰动区的传播过程.射线追踪是研究电离层电波传播的有效方法之一,尤其对高频以上频段电波信号,射线追踪方法能够准确描述电波的传播路径.射线追踪可以分为数值法射线追踪和解析法射线追踪两种,解析法射线追踪不能应用于非均匀的电离层,其应用受到局限;数值法射线追踪可以应用于非均匀电离层,本文采用二维射线追踪方法研究电波信号在扰动区的传播效应.由于射线追踪算法十分成熟,在此不再赘述,详细算法请查阅文献[33,34].

图4以释放后10 s扰动区的电子密度分布为背景,研究了12—15 MHz电波信号在扰动区的传播过程.释放后10 s电离层洞的直径约30 km,电子密度增强区厚度约10 km,最大电子密度值约1.82×106cm−3.

从图4可以看出,11 MHz无线电波全部被电子密度增强区反射,12—14 MHz无线电波部分穿越电子密度增强区,部分被电子密度增强区反射,穿越电子密度增强区的电波信号产生了显著的聚焦效应,聚焦效应随电波频率的减小而增强.聚焦效应是由于空洞区域介电系数大于背景电离层介电系数产生的,根据电离层色散介质的特性,频率越小的电波介电系数增加越大,聚焦效应越明显.

图5以释放后120 s扰动区的电子密度分布为背景,研究了9—12 MHz电波信号在电子密度扰动区的传播过程.释放后120 s电离层洞的直径约70 km,电子密度增强区厚度约50 km,最大电子密度约1.12×106cm−3.

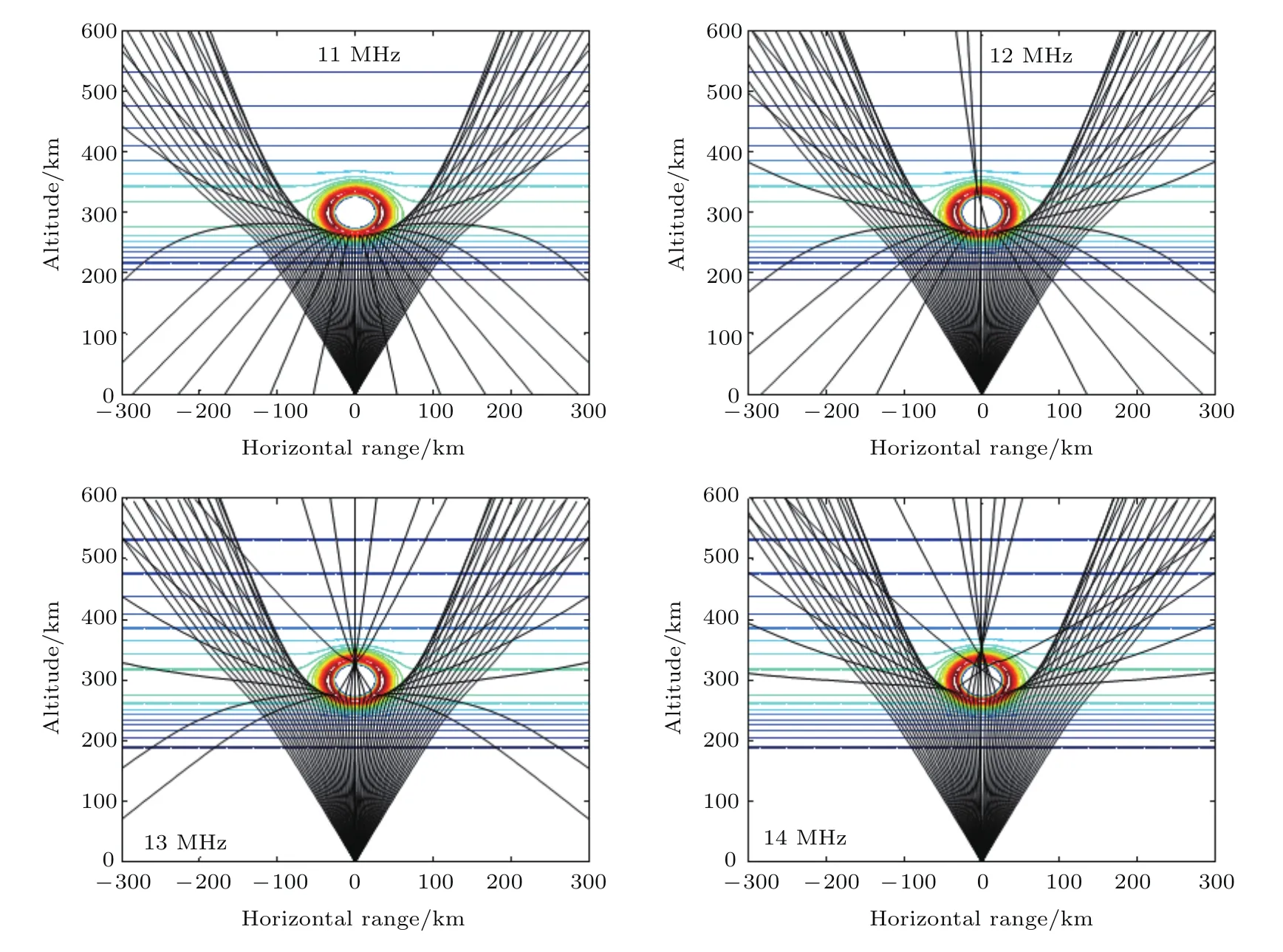
图4 短波信号在强反射区中的传播Fig.4.The transmission of short wave signals in strong re fl ection areas.

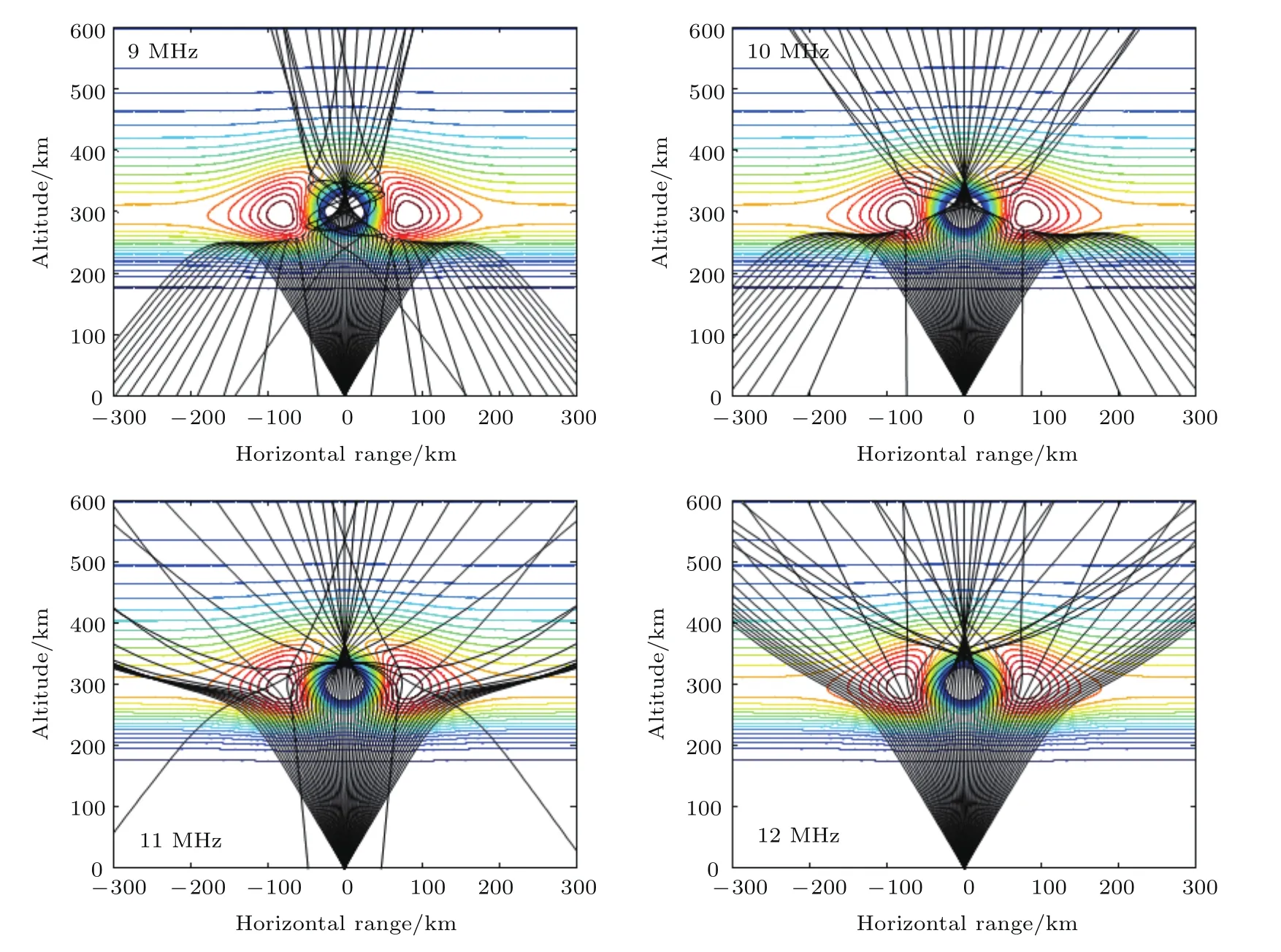
图5 短波信号在强反射区中的传播Fig.5.The transmission of short wave signals in strong re fl ection areas.

从图5可以看出,9 MHz无线电波在电离层洞内经过多次绕射,部分信号穿越电离层洞,部分信号反射回地面,而传播到电子密度增强区的无线电波,被电子密度增强区反射回地面.10—11 MHz无线电波在电离层洞内产生了聚焦效应,而后穿越电离层洞,而传播到电子密度增强区的无线电波,部分信号穿越增强区,另一部分信号反射回地面.12 MHz无线电波在电离层洞内聚焦,在电子密度增强区散焦后全部穿越扰动区.

在一次利用探空火箭开展的空间物理试验中,位于试验区的电离层垂直探测仪在火箭发射后观测到了电子密度突然增强现象[35].该火箭为固体火箭,火箭喷焰的主要产物为H2O和CO2等,主要为电子密度耗空类化学物质.火箭发射前电离层临界频率为7.3 MHz,发射后154 s在F层高度出现一条强反射描迹,最高反射频率超过12 MHz(如图6(b)[35]所示).本次试验观测到强反射描迹极有可能是释放初期,释放气体快速膨胀挤压背景等离子体,引起边界处等离子体密度升高产生的.

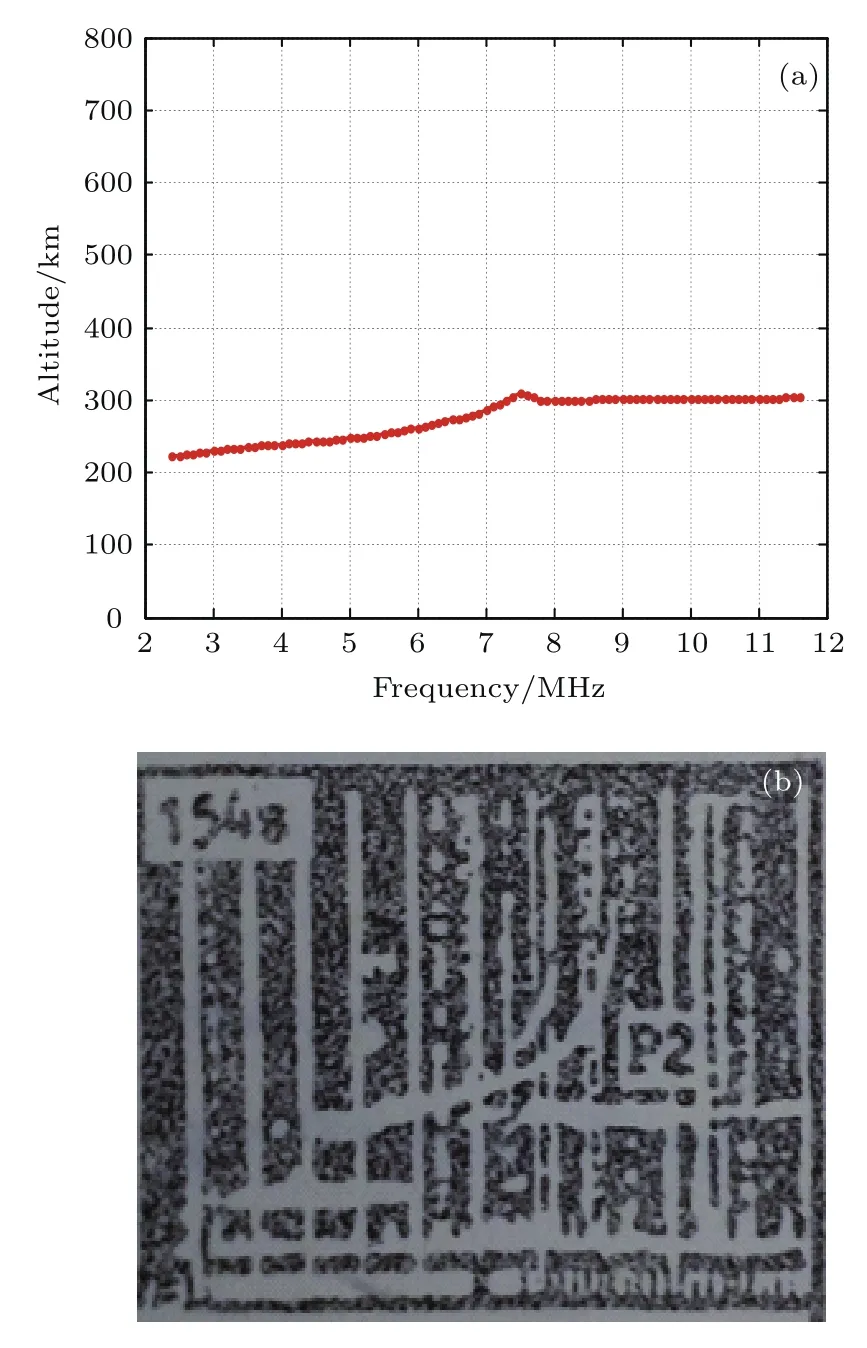
图6 人工强反射区仿真电离图和实测电离图对比Fig.6.The comparison between the simulated ionogram and the measured ionogram in the arti fi cial strong re fl ection zone.

根据无线电波在电离层扰动区的传播规律和本文虚拟的试验场景,采用射线追踪方法反演得到了释放后30 s的垂测电离图(如图6(a)所示).反演得到的电离图与实测电离图吻合较好,初步验证了本文建立的释放早期的试验效应物理模型的正确性.由于缺少空间主动试验的实测数据,本文无法开展数值模拟结果与实测结果的详细对比研究,随着我国空间主动试验的开展,该模型将进一步完善和改进.

5 总结与讨论

在电离层高度释放中性气体能够引起电离层电子密度耗空,在释放之后快速形成电离层洞;同时,由于释放中性气体的快速膨胀,挤压背景等离子体,在电离层洞的外边缘产生“壳状”电子密度增强结构,电离层洞和电子密度增强结构同时存在是释放早期试验效应的显著特征.本文研究了电离层中性气体释放的早期试验效应,建立了早期试验效应物理模型,仿真了释放早期电子密度的时空演化过程.释放后1 s增强区最大电子密度达2.46×106cm−3,约为背景电子密度的2.8倍,随后边界处的电子密度逐渐降低;释放后30 s,最大电子密度约1.58×106cm−3,约为背景电子密度的1.7倍;释放后120 s,增强区的最大电子密度约1.12×106cm−3,约为背景电子密度的1.2倍.在释放后2 min内,电离层洞的尺度逐渐增加,释放后5 s释放物分布范围为直径约10 km的球体,释放后120 s释放物分布直径达70 km以上,同时电离层洞的耗空深度缓慢降低,释放后1 s电离层洞100%耗空,到释放后120 s电离层洞耗空深度约为95%.

在300 km高度释放40 kg SF6,以释放后10 s和120 s的效应仿真结果为研究场景,采用射线追踪方法研究了不同频率电波信号在扰动区的传播效应.释放后10 s电子密度增强效应十分显著,增强区厚度约10 km,最高可反射14 MHz的无线电波信号.释放后120 s电子密度增强现象减弱,增强区厚度增加,最高可反射11 MHz的无线电波,9—12 MHz无线电波在扰动区发生了复杂的绕射、聚焦和散焦等传播效应.根据电离层垂测仪工作原理和射线追踪理论,反演得到了释放后30 s的电离层垂测电离图,电离图上出现了明显了附加增强描迹,最高反射频率达11.6 MHZ.反演结果与一次火箭喷焰的实际观测数据吻合较好,初步验证了本模型的正确性.

电离层中性气体释放早期试验效应物理模型,重点研究释放后2 min内电离层扰动效应的演化过程,是电离层中性气体释放物理模型的重要改进,更为准确地描述了释放后2 min内扰动区电子密度的时空演化过程.

[1]Booker H G 1961J.Geophys.Res.66 1073

[2]Mendillo M,Hawkins G S,Klobuchar J A 1975Science187 343

[3]Mendillo M,Hawkins G S,Klobuchar J A 1975J.Geophys.Res.80 2217

[4]Zinn J,Sutherland C D,Stone S N,Duncan L M,Behnke R 1982J.Atmos.Terr.Phys.44 1143

[5]Mendillo M,Jeffrey M,Forbes J M 1978J.Geophys.Res.83 151

[6]Mendillo M,Forbes J M 1982J.Geophys.Res.87 8273

[7]Mendillo M,Smith S,Coster A,Erickson P,Baumgardner J,Martinis C 2008SPACE WEATHER6 S09001

[8]Anderson D N,Bernhardt P A 1978J.Geophys.Res.83 4777

[9]Paul A,Bernhardt P A 1979J.Geophys.Res.84 4341

[10]Paul A,Bernhardt P A 1979J.Geophys.Res.84 793

[11]Bernhardt P A 1982J.Geophys.Res.87 7539

[12]Bernhardt P A 1984J.Geophys.Res.89 3929

[13]Bernhardt P A,Weber E J,Moore J G,Baumgardner J,Mendillo M J 1986Geophys.Res.Lett.91 8937

[14]Zhao H S,Xu Z W,Wu Z S,Feng J,Wu J,Xu B,Xu T,Hu Y L 2016Acta Phys.Sin.65 209401(in Chinese)[赵海生,许正文,吴振森,冯杰,吴健,徐彬,徐彤,胡艳莉2016物理学报65 209401]

[15]Hunton D E 1993Geophys.Res.Lett.20 563

[16]Koons H C,Rocdcr J L 1995J.Geophys.Res.100 5801

[17]SchunkR W,Szuszczewicz E P 1988J.Geophys.Res.93 12901

[18]Schunk R W,Szuszczewicz E P 1991J.Geophys.Res.96 1337

[19]Drake J F,Mulbrandon M,Huba J D 1988Phys.Fluids31 3412

[20]Zalesak S T,Drake J F,Huba J D 1988Radio Sci.23 591

[21]Zalesak S T,Drake J F,Huba J D 1990Geophys.Res.Lett.17 1597

[22]Ma T Z,Shunk R W 1991J.Geophys.Res.96 5793

[23]Ma T Z,Shunk R W 1993J.Geophys.Res.98 323

[24]Gatsonis N A,Hastings D E 1991J.Geophys.Res.96 7623

[25]Shuman N S,Hunton D E,Viggiano A A 2015J.Chem.Rev.115 4542

[26]Schunk R W,Szuszczewicz E P 1991J.Geophys.Res.96 1337

[27]Doles J H,Zabusky N J,Perkins F W 1976J.Geophys.Res.81 5987

[28]Zhao H S,Feng J,Xu Z W,Wu Z S 2016J.Geophys.Res.121 10508

[29]Zabushky N J,Doles J H,Perkins F W 1973J.Geophys.Res.78 711

[30]Lloyd K H,Haerendel G 1973J.Geophys.Res.78 7389

[31]Bernhardt P A 1984J.Geophys.Res.89 3929

[32]Bernhardt P A 1987J.Geophys.Res.92 4617

[33]Haselgrove J 1955Proc.Phys.Soc.London23 355

[34]John M Kelso 1968Radio Sci.3 1

[35]Zhang R F 1986Proceedings of the International Symposium on Space PhysicsBeijing,China,November 10–14,1986 pp5–100