奇异谱分析用于提升双光梳激光测距精度∗

曹辉 宋有建 于佳禾 师浩森 胡明列 王清月

(天津大学精密仪器与光电子工程学院,光电信息技术教育部重点实验室,天津 300072)

1 引 言

长度是国际单位制中的七个基本单位之一,同时也是科学研究与工业生产中最常用的物理量之一.近年来,卫星编队飞行、大型工件形貌测量等领域对大量程、高精度的绝对距离测量提出了很高的要求.

传统的光学方法测量绝对距离主要分为干涉法[1]和飞行时间法[2].干涉法使用单色光测距,其分辨率受限于单色光的波长稳定性,分辨率可以达到纳米量级.但是光干涉法的绝对距离测量范围仅为测量光的半波长,对于更长的待测距离只能通过增量式测量获取距离值.飞行时间法通过测定激光脉冲的发射时刻和其回波返回时刻之间的时间差推算距离信息.该方法具有测量范围大、发射功率高以及抗干扰能力强等优点.但是,该方法的时间分辨率受限于光电探测器的响应带宽,仅能达到皮秒量级,即毫米级的距离分辨率.

基于飞秒激光的飞行时间测距,有效地克服了干涉法以及传统飞行时间法的上述缺点,有效地提升了绝对距离测量精度,在航空航天、遥感和表面形貌测量等领域有着很好的应用前景.2000年,Minoshima和Matsumoto[3]首次提出基于飞秒激光的绝对距离测量,实现了240 m长的高精度飞行时间测量.2009年,Coddington等[4]使用两台相干的光纤激光频率梳(双光梳)在约1.5 m的测试距离下实现了5 nm的测试精度,并同时实现了对运动物体的追踪锁定.2010年,Lee等[5]在飞秒激光测距系统中使用平衡光学互相关(BOC)技术,通过等效采样原理成功地避免了采用光电探测器对光脉冲直接进行光电接收引入的时间分辨率损失,将1 s内采集到的测距信号进行平均,在0.7 km的距离下达到了7 nm的绝对测量精度.2012年,秦鹏等[6]基于平衡互相关技术,采用掺Yb锁模光纤激光器作为测距光源,在52 m的待测距离上,获得了12 nm的绝对距离测量精度.2013年,邢书剑等[7]采用基于改进的迈克耳孙干涉原理的任意绝对距离测量系统,使用飞秒光学频率梳在0.6 m时获得了0.5µm的测距精度.2016年,张晓声等[8]使用飞秒激光模间拍频法实现了优于3µm的绝对测量精度.

在已有的飞秒激光测距方法中,双光梳方法由于测量精度高、更新速率快,并可以同时跟踪多个目标,引起了广泛的关注.尤其是通过使用两台自由运转锁模激光器(简化的双光梳),实验装置可以极大地简化,同时能够保证微米级的测量精度,对工业测量具有极大的吸引力.但是,双梳测距极容易受到激光器中量子噪声的影响,从而增加测量结果的不确定度,使测量精度下降[9].尽管可以使用滑动平均等方法减轻上述问题,可是必须以降低系统的更新速率为代价.另外,滑动平均会在距离信号本身带有高频成分或者噪声源更加复杂的情况下失效.

奇异谱分析(SSA)是一种从含噪信号中提取量化信息的方法.它基于Takens的嵌入理论,在1986年由Broomhead和King共同建立[10].SSA方法是一种无参数频谱估计技术,它用于分析无先验知识的动态系统采集到的时间序列,并从中提取若干有实际意义的成分[11].同时,SSA是一种无模型方法,可以应用于线性和非线性系统中.SSA广泛应用于地理学[12]、经济学[13]和社会学[14]等数据较为复杂的学科中.此外有报道SSA方法用于季节性GPS信号的分析[15],显示了SSA对于提取GPS中的调制振荡信号是一种完备的方法.在高光谱遥感中,SSA也表现出有效的信号提取功能[16−19].

本文应用SSA方法分析由高更新速率双光梳测距系统获得的飞行时间绝对测距数据,证明了在无先验随机噪声模型的前提下,SSA方法可以用来提取含噪一维阶梯结构信号.进一步在实验中利用200 Hz更新速率的简化的双光梳测距系统,对移动的合作靶的位置进行了测定,通过SSA方法对获得的信号进行分析,经由后处理所提取出的信号标准差达到0.15µm.

2 原 理

2.1 双光梳测距原理及系统参数

图1 自由运转双梳激光测距系统,插图为经“时间展宽”的脉冲回波信号Fig.1. Dual-comb free-running laser ranging system working at 1550 nm. The inset illustrates the equivalently-sampled Target/Reference-re fl ected pulses in the “stretched” time frame.HWP(half wave plate);LO(local oscillator);LUT(laser under test);PBS(polarization beam splitter);PD(photo detector);PPKTP(periodically poled KTiOPO4);QWP(quarter wave plate).

双光梳测距系统的测距原理是基于光学等效采样方法将超快的周期性脉冲信号在时间上“展宽”,从而可以应用现有的电子学手段提取并解算脉冲飞行时间,进而计算得出飞秒激光源和目标之间的绝对距离.系统结构如图1所示,主要由飞秒激光源、光学互相关系统和数据采集处理系统组成.实验中采用两台相互独立的自由运转被动锁模飞秒激光器,分别作为本地振荡器(local oscillator,LO)和信号激光源(laser under test,LUT).两台激光器均为全保偏光纤激光器,使用碳纳米管(carbon nanotube,CNT)作为可饱和吸收材料,工作波长约为1550 nm,输出平均功率分别为10 mW和13 mW,重复频率约为74 MHz,且两台激光器之间有约为2 kHz的重复频率差.信号光经过准直器和半波片(half wave plate,HWP)后,经由偏振分光棱镜(polarization beam splitter,PBS)分束,分得的两束光分别经过参考镜和目标镜反射,经反射的参考脉冲序列和目标脉冲序列分别与LO脉冲序列合束,经过基于PPKTP(periodically poled KTiOPO4)晶体的光学互相关系统采样,并使用光电探测器(photo detector,PD)接收采样信号.由于本地振荡器和信号激光源具有一定的重复频率差∆fr,该值远小于激光器本身的重复频率fr,因此产生等效采样效果,即飞行时间被展宽,其展宽倍数为N=fr/∆fr.在实际应用中,并不需要测定放大率N,只需要测得到达探测器获得的互相关信号脉冲峰值的时间即可由下式计算绝对距离D:

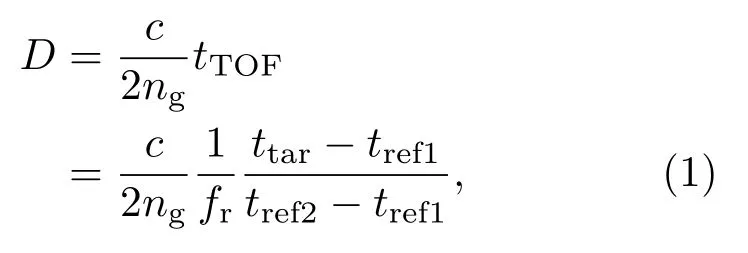
其中c表示真空光速,ng表示空气群折射率,tref1和ttar分别表示一个周期内的参考脉冲和目标脉冲到达探测器的时刻,tref2表示下一个周期的参考脉冲到达探测器的时刻.激光实验装置的详细设定参照文献[9].

2.2 奇异谱分析原理

在没有运动模型和随机过程模型的前提下,为了实现信号与噪声的分离,本文用SSA方法对飞秒激光距离信号进行处理.SSA方法将观测到的时间序列信号分解为一系列独立分量的总和,并赋予每个分量相应的物理意义(例如,慢变信号、周期振荡信号和随机噪声).经典SSA方法分为以下四个步骤:数据内嵌、奇异值分解(singular value decomposition,SVD)、对角平均和分组重建.

首先,通过等间隔采样获得包含N个采样点的初始数据集YN,

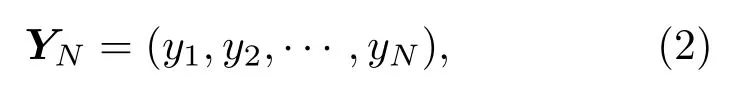
其中yi表示第i个采样点.单个采样点包含的数据个数称为该观测数据的维度(例如,对于同时采集目标位置与速度的系统,每个采样点包含位置和速度两个数据,即观测数据维度为2).数据采集时需要保证采样点数N远远大于观测数据的维度.选定时间嵌入窗口,其长度为整数L,满足2≤L≤N/2,对初始数据集YN进行延迟坐标映射,即选取L个连续采样点,以获得时滞向量xi,

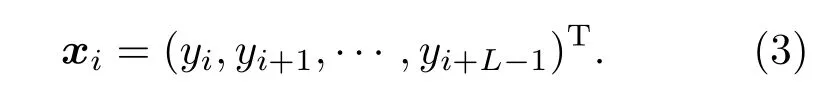
因此可以由初始数据集YN获得N−L+1个时滞向量.这些时滞向量又可以组成轨迹矩阵X,

在第二步奇异值分解中,对轨迹矩阵X进行奇异值分解,即得到

其中矩阵U和V均为列归一化矩阵,矩阵Σ为对角矩阵.U的列向量组{ui}和V的列向量组{vi}分别为矩阵XXT和XTX的正交归一化本征矢.列向量组{ui}和{vi}又被分别称为矩阵X的经验正交函数(EOF)和主成分(PC).每一个经验正交函数和主成分对{ui,vi}都对应一个矩阵X的奇异值σi,其大小可衡量相应经验正交函数和主成分在原始信号中的占比,该值大小等于矩阵XXT中与相应经验正交函数ui所对应的本征值的平方根.

考虑到经过SVD分解后所得的矩阵数量d=rankX,轨迹矩阵X还可以表示为

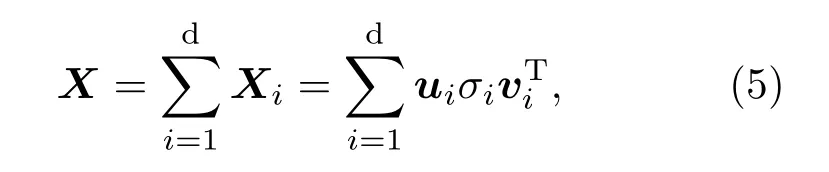
其中Xi表示通过SVD分解获得的第i个矩阵.对于每个矩阵Xi,本征矢和本征值对(ui,σi,vi)按照奇异值降序进行排列,即σ1≥σ2≥···≥σd≥0.

第三步,对角平均.由于上一步获得了分解后的若干轨迹矩阵分量,这里需要将其还原为原始信号的数据结构.因此还原后的信号为对应矩阵的副对角线元素的平均值.设还原后的信号重建成分(RC)Y(i)的各元素和相应矩阵中元素的对应关系如下:

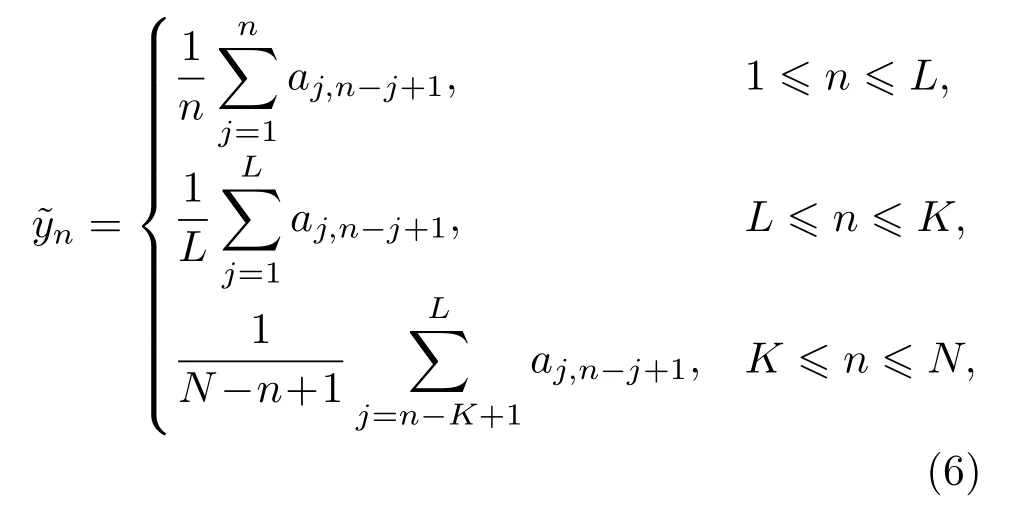
最后,将得到的还原后的RC进行分组,进而可以获得重建信号和噪声的分离.通常按照趋势、振荡和噪声进行分类.实际应用中根据经验,一般前几个RC归为趋势类,即重建信号本身.归类后的RC需要按照类别进行累加,以获得相应分类的重建信号.由于本文所应用场景不包含振荡信息,因此信号本身仅仅包含趋势和噪声成分.

3 SSA方法对双光梳测距系统数据的处理分析

3.1 仿真实验

首先使用仿真数据验证SSA对任意有色噪声的提取能力.仿真了双光梳测距系统对一维物体的扫描以得到其表面形貌的应用场景.待测一维物体为1µm高的台阶,如图2青绿线所示.仿真测量以200 Hz更新速率持续2 s,获得了400个采样点,测量结果如图2黑线所示.这里测量信号采用仿真紫色噪声进行劣化,噪声标准差为0.3µm.

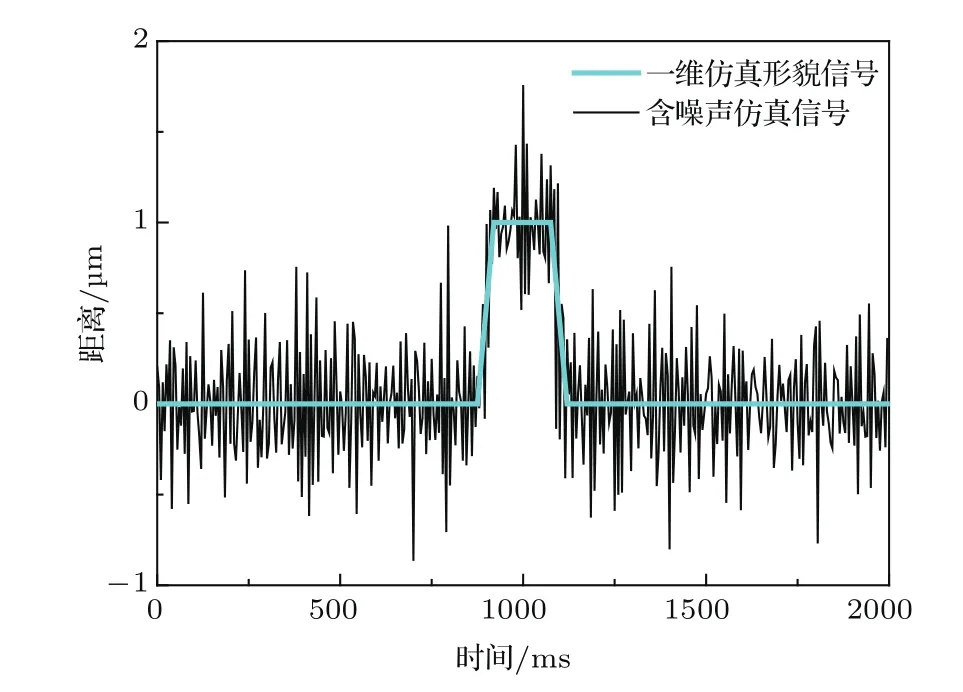
图2 原始一维仿真测距数据(青绿线);被0.3µm标准差的紫色噪声劣化后的仿真数据(黑线).Fig.2.The original 1-D signal with a 1µm step(cyan curve)and the same signal embedded in computergenerated violet noise with a standard deviation 0.3µm(black curve).

图3 SSA方法应用于信号提取及噪声分离 (a)一维含噪声形貌信号及重建信号;(b)提取的紫色噪声时域波形;(c)噪声功率谱密度Fig.3.Signal extraction simulation by using SSA method:(a)1-D pro fi le embedded in violet noise and its reconstruction;(b)time domain value of the extracted violet noise;(c)PSD of the extracted noise.

通过上述对SSA方法的描述可知,在SSA中惟一的参数为嵌入窗口长度L.对于上述仿真数据,我们选取窗口长度L=50,同时提取信号和噪声.重建信号通过选取所需的分解模式并累加而获得,如图3(a)青绿线所示.同时,由于仿真信号不含有振荡,因此可以将剩下的分解模式进一步累加,以对噪声进行提取.获得的噪声如图3(b)所示,其标准差为0.29µm,噪声功率谱如图3(c)所示,由于其功率谱密度斜率为f2,为紫色噪声,表明SSA方法可以很好地提取噪声的类型.此外,如果将提取后的信号和噪声相加,即可获得原始信号,这也说明了SSA方法对信号的分解是可逆的,不会造成原始信号的信息丢失.

3.2 实验分析

使用2.1节中描述的双光梳测距系统测定约0.5 m处的目标靶的距离.目标靶装载于线性平移台,以约2µm步长进行移动.图4(a)中黑线所示为采集到的原始信号,测量更新速率为200 Hz,测量标准差为1.9968µm.

针对上述采集到的距离信号,选取L=40的嵌入窗口长度.发现40个分解成分中的第一个可以作为重建信号,如图4(a)青绿线所示,其测量标准差为0.1522µm.通过对比原始数据的标准差,可以看出SSA方法对双光梳测距系统精度具有显著的提升作用,测距精度提升了13倍左右.

剩余的39个分解成分可以归类为随机噪声,累加后重建为提取噪声,时域波形如图4(b)所示,其标准差为1.88µm,功率谱如图4(c)所示,由于其功率谱密度为水平曲线,显示出测距系统精度主要受到白噪声的影响.

进而,还可以分析SSA方法在更远的测距量程下的适用性.考虑远距离双梳测距,空气折射率的估计误差和飞秒光源的重复频率的测量误差分别会以10−7×D和10−9×D引入测量不确定度[9].因此,在大气层内的远距离测距不确定度主要由空气折射率估计误差主导;而在真空中,比如星间高精度基线测量,测量不确定度则完全由飞秒光源的重复频率的测量误差引入.以上两种误差因素均具有随机噪声的属性,可以通过SSA方法分离误差与信号,达到减小测量不确定度的目的.

图4 双光梳测距系统的直接测距结果与SSA分析 (a)实验测得的激光器和目标之间距离的原始数据及SSA提取结果;(b)提取的噪声时域波形;(c)噪声功率谱密度Fig.4.Signal obtained from a dual-comb laser ranging system and data processing results by using SSA method:(a)The measured distance of a moving target and its reconstructed signal;(b)time domain value of the extracted noise;(c)PSD of the extracted noise.

4 结 论

本文应用SSA这种无模型方法处理含噪飞行时间法距离信号.通过SSA,可以在没有任何运动模型和随机过程假设的前提下同时提取信号和噪声.这表明SSA对于重建测距信号和提取系统噪声是一种有效的分析工具.在仿真实验中,高精度地提取了含有紫色(功率谱密度斜率为f2)噪声的一维阶梯信号.实验中,采用200 Hz更新速率的简化的双光梳测距系统追踪移动合作靶的位置.通过SSA对信号的后处理,将合作靶的距离信息有效地从量子噪声中提取出来,并获得了0.1522µm的测距精度.值得注意的是,SSA方法本身对信号维度没有任何要求,因此很容易扩展到高维情况.这意味着SSA辅助下的飞秒激光测距系统可以用于物体表面形貌测量,尤其对含有非连续台阶结构的大规模集成电路印刷版的缺陷检测等具有潜在的应用价值.

[1]BobroffN 1993Meas.Sci.Technol.4 907

[2]Smullin L D,Fiocco G 1962Nature194 1267

[3]Minoshima K,Matsumoto H 2000Appl.Optics39 5512

[4]Coddington I,Swann W C,Nenadovic L,Newbury N R 2009Nat.Photonics3 351

[5]Lee J,Kim Y J,Lee K,Lee S,Kim S W 2010Nat.Photonics4 716

[6]Qin P,Chen W,Song Y J,Hu M L,Chai L,Wang C Y 2012Acta Phys.Sin.61 240601(in Chinese)[秦鹏,陈伟,宋有建,胡明列,柴路,王清月2012物理学报61 240601]

[7]Xing S J,Zhang F M,Cao S Y,Wang G W,Qu X H 2013Acta Phys.Sin.62 170603(in Chinese)[邢书剑,张福民,曹士英,王高文,曲兴华2013物理学报62 170603]

[8]Zhang X S,Yi W M,Hu M H,Yang Z H,Wu G H 2016Acta Phys.Sin.65 080602(in Chinese)[张晓声,易旺民,胡明皓,杨再华,吴冠豪2016物理学报65 080602]

[9]Shi H,Song Y,Liang F,Xu L,Hu M,Wang C 2015Opt.Express23 14057

[10]Broomhead D S,King G P 1986Physica D20 217

[11]Vautard R,Ghil M 1989Physica D35 395

[12]Vautard R,Yiou P,Ghil M 1992Physica D58 95

[13]Hassani H,Zhigljavsky A 2009J.Syst.Sci.Complex.22 372

[14]Hassani H,Webster A,Silva E S,Heravi S 2015Tourism Manage.46 322

[15]Chen Q,van Dam T,Sneeuw N,Collilieux X,Weigelt M,Rebischung P 2013J.Geodyn.72 25

[16]Zabalza J,Ren J,Wang Z,Marshall S,Wang J 2014IEEE Geosci.Remote S.11 1886

[17]Zabalza J,Ren J,Wang Z,Zhao H,Wang J,Marshall S 2015IEEE J.Sel.Top.Appl.8 2845

[18]Zabalza J,Ren J,Zheng J,Han J,Zhao H,Li S,Marshall S 2015IEEE T.Geosci.Remote53 4418

[19]Rafert J B,Zabalza J,Marshall S,Ren J 2016Appl.Spectrosc.70 1582