地面核磁偏共振响应特征与复包络反演方法∗

蒋川东 王琦 杜官峰 易晓峰 田宝凤

1)(地球信息探测仪器教育部重点实验室(吉林大学),长春 130061)

2)(吉林大学仪器科学与电气工程学院,长春 130061)

3)(吉林大学通信工程学院,长春 130012)

1 引 言

地面核磁共振(surface nuclear magnetic resonance,SNMR)是一种以非侵入方式直接定量探测地下水水文参数的地球物理方法[1].与常见的核磁共振成像和核磁共振测井[2]等核磁共振技术的基本原理相同,SNMR具有对地下水含量分布成像和评估地层孔隙尺寸的能力[3].在地磁场(B0)中,地下水中的氢质子(1H)的核磁矩绕B0方向旋进,并沿B0方向产生宏观磁化矢量M,其角频率ωL=|γB0|称为Larmor角频率,其中γ为1H磁旋比.通过在地表铺设线圈并发射Larmor频率(fL=ωL/2π)的交变磁场B1,M绕B1方向倾倒,产生横向分量M⊥.当发射停止时,B1消失,M⊥绕B0做Larmor进动,同时在接收线圈中产生感应信号,称为自由感应信号(free induction decay,FID)[4].通常发射频率(fT)与fL相等,称为共振激发(on-resonance excitation);当fT与fL不相等时,称为偏共振激发(off-resonance excitation).在实际应用中,不可避免地会出现偏共振现象,如果近似为共振则会导致地下水成像结果不准确.因此本文以地面核磁偏共振(surface nuclear magnetic off-resonance,SNMOR)为主要研究目标,分析和讨论偏共振激发时各种因素对SNMOR信号的影响.

Larmor频率fL取决于B0的大小,影响B0的因素有以下四个方面：1)B0的不均匀性,由于地层介质和水的磁化率不同[5],B0在地层内部存在差异,近似为柯西-洛伦兹分布[6,7];2)B0的时变性,在同一个地点,B0的日平均变化量为70—120 nT,对应的fL变化在±5 Hz范围内[8];3)磁性介质干扰.当测量区域存在铁磁性矿产或大量金属干扰时,B0会出现异常变化(＞100 nT),使得fT与fL的偏离量达到5 Hz以上[9];4)电磁噪声,在强电磁噪声环境中,无法准确获得B0,利用频率估计值fT发射,与fL存在偏差[10].因此,B0随时间和空间变化、或受噪声干扰都会出现测量不准确的情况,fT与fL不同将会发生SNMOR现象,利用仪器获得的信号幅度和相位均不同于SNMR.如果采用传统的共振模型对含水量和弛豫时间(T∗2)等水文参数进行反演,将会严重影响结果的准确度.

针对SNMOR,Walbrecker等[11]首先分析了偏共振激发时频率偏量∆f=fT−fL对FID信号幅度和相位的影响.Grombacher等[12]利用偏共振现象,提出组合激发序列方式,通过优化发射频率提高FID信号的幅度.Irons和Li[13]提出基于洛伦兹变换的正反演模型,解决由B0不均匀性引起的FID信号失相(dephasing)问题.Grombacher等[14]讨论了多种B0不均匀情况下的仿真模型,以及由此引起的含水量反演误差;并提出了频率环(frequency-cycling)激发序列,解决在fL未知时的探测问题[15].但是,以上研究主要集中在∆f对SNMOR信号和反演结果的影响,没有涉及利用∆f修正SNMOR模型,进而提高含水量和T∗2反演准确度的问题.目前,QT反演(pulse to time inversion,QTI)是最稳定的反演方法[16],该方法只利用信号包络的幅度信息,忽略其相位参数.Roy和Lubczynski[17]提出信号初始幅度和初始相位同时参与的反演方法,在低噪声环境情况下可提高对深部含水层的解释准确度.Chen等[18]也提出了利用初始信号实部和虚部参与反演提高含水量解释准确度的方法.但是,这些反演方法只利用FID信号的初始值,存在不稳定的问题,而且只考虑了电阻率信息引起的相位偏量,没有考虑∆f引起的相位偏量.因此,基于∆f建立SNMOR模型,同时利用FID信号包络的实部和虚部进行复包络反演,将会提高地下水反演准确度和稳定性.

本文针对偏共振激发产生的SNMOR现象,分析SNMOR响应信号特征,提出自动搜索相位偏量的复包络反演方法(complex envelope inversion,CEI).首先,从SNMR的基本原理入手,推导偏共振下的磁矩和灵敏度核函数的表达式,研究了∆f对FID信号的影响;其次,提出相位偏量的自动搜索方法,实现CEI反演算法;第三,通过仿真模型分析SNMOR信号的特征和∆f对反演结果的影响;最后,利用野外实测数据证明SNMOR模型和CEI的有效性和准确性.

2 SNMOR原理

根据NMR原理,FID信号表达式为[1]

其中,q=I0τp称为激发脉冲矩,是发射电流强度I0和持续时间τp的乘积;V0是初始振幅,与含水量w(含水体积与总体积之比)成正比;T∗2是横向弛豫时间,与孔隙大小相关;ϕ0是初始相位,与地下电阻率(ρ)、线圈空间位置、频率偏差(∆f)和仪器系统等多种因素有关.根据SNMR正演理论[19],信号初始振幅V0表示为

其中,K称为灵敏度核函数,即单位含水量产生的FID信号大小;r为探测体积vol内的坐标.

2.1 激发磁化矢量

地面上的发射线圈产生的激发磁场B1(ωL,I0,ρ,r)是发射频率ωL、电流强度I0、地下电阻率ρ和空间位置r的函数,可利用有限元等方法计算[20]. 由于存在地磁倾角I和地磁偏角D,只有垂直于地磁场B0方向的分量B⊥对FID信号有贡献,B⊥(ωL,I0,ρ,r,I,D)=RIRDB1(ωL,I0,ρ,r)(其 中RI和RD为 旋 转 矩阵[10],以下简记为B⊥).在地磁场B0和激发磁场B⊥作用下,氢质子自旋产生的宏观磁化矢量M用Bloch方程[21]表示:

其中,Beff代表有效激发磁场;ˆx,ˆy和ˆz代表以fT为频率的旋转坐标系的单位向量,ˆz的方向与B0相同;T1是纵向弛豫时间.Beff具体表示为

1)共振激发(fT=fL)

当∆f=0 Hz时,Beff=B⊥即发生SNMR现象,B1在导电介质中发生椭圆极化[22].由于平行于B0方向的分量B⊥z非常微弱,B⊥在旋转坐标系下可以表示为

其中,ϕ=ϕT+ϕσ,即发射电流相位ϕT与电导率引起的极化相位ϕσ之和.

在理想条件下,忽略激发期间的弛豫现象[23]和假设发射电流包络为矩形脉冲,求解表达式(3),

此时,B⊥和τp决定了共振激发的扳倒角度θon=|γB⊥|τp. 通过控制ϕT=0, 得到在共振时单位磁化矢量Mon在垂直于B0方向(ˆz方向)的平面上(ˆx-ˆy平面)的分量M⊥,on为

因此,对于共振激发,M⊥,on在ˆx方向上为0,只在ˆy方向上存在分量.

2)偏共振激发(fT̸=fL)

当∆f=0 Hz,发生SNMOR现象,由表达式(4),Beff不但与B⊥有关,还在方向上存在与∆f相关的分量∆B0=2π∆f/γ.由表达式(3)描述的感应扭矩导致了在Beff方向上的章动,与平面的方向角度α=∆B0/|B⊥|.此时有效的扳倒角度为单位磁化矢量Moff的垂直分量M⊥,off表示为

图1(a)解释了当∆f=0 Hz(虚线)和4 Hz(实线)时,M⊥的单位方向矢量(即对M⊥幅度归一化)在旋转坐标系上的运动轨迹.在共振(∆f=0 Hz)时,扳倒角度为θon,M⊥,on只在ˆy方向上存在分量.而对于偏共振(∆f=0 Hz)时,扳倒角度为θoff,M⊥,off在ˆx和ˆy方向上均存在分量,因此偏共振激发产生了额外的相位偏差ϕ∆f,见图1(b)所示.

图1 旋转坐标系下共振激发和偏共振激发的磁化矢量轨迹图(a)M在三维坐标上的运动轨迹;(b)M在ˆx-ˆy平面运动轨迹的二维投影Fig.1. Trajectory of magnetization in a rotating reference frame during on-resonance and off-resonance excitation:(a)Trajectory of M in three dimensional coordinates;(b)trajectory projection of M in two dimensional coordinates.

2.2 灵敏度核函数

根据表达式(1)和(2),当发射线圈和接收线圈共线时,接收磁场BR与激发磁场B1相等,K表示为[18]

其中,M⊥在共振时取M⊥,on,在偏共振时取M⊥,off;M0是净磁化矢量;ξ是发射和接收磁场由于椭圆极化产生的相位分量.对于一维层状大地模型,SNMOR的正演表达式可以化简为

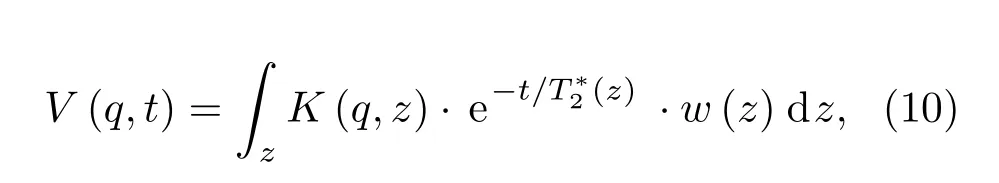
其中,V为FID信号的复包络,z为深度.图2分别计算了在SNMR和SNMOR模型中,K的实部和虚部随z和q变化的结果.仿真正演模型为：B0为54721 nT,fT为2330 Hz,I为60°,D为0°,ρ为100 Ωm均匀分布,线圈为边长100 m的正方形,q设置为0.01—12 As,按对数分布,数量为24个,τp为40 ms.如图2(a)—(c)所示,K的实部图像在∆f=−3,0和3 Hz时基本一致,主要信号(黄色部分)随深度增加,所需q也相应增加,且幅度逐渐减小,说明含水层深度增加,探测难度逐渐增大.图2(d)—(f)中K的虚部图像在∆f=−3,0和3 Hz时呈现完全不同的结果.对于共振,因为m⊥,on无额外的相位,K的虚部几乎为0,其中较小的数值是由ρ引起的ϕρ,可以忽略.而对于偏共振,M⊥,off在Mx和My均有分量,因此产生了额外的相位ϕ∆f,K的虚部信号明显增加,而且∆f=−3 Hz(蓝色部分)和3 Hz(黄色部分)的符号相反.因此,相比于SNMR,SNMOR能够获得额外的虚部信息,更强的信号幅度和更多的相位信息有利于反演地下的含水层分布.

图2 在SNMR和SNMOR模型下,K随q和z变化的图像 (a)∆f=−3 Hz,(b)∆f=0 Hz,(c)∆f=3 Hz时K的实部;(d)∆f=−3 Hz,(e)∆f=0 Hz,(f)∆f=3 Hz时K的虚部Fig.2.Complex kernel function K with q and z in SNMR and SNMOR models:(a)∆f=−3 Hz,(b)∆f=0 Hz,(c)∆f=3 Hz,the real part of K;(d)∆f=−3 Hz,(e)∆f=0 Hz,(f)∆f=3 Hz,the imagery part of K.

3 复包络反演方法

由SNMOR的原理和正演模型得到接收线圈获得的V是复数,其相位与发射电流相位ϕT(可控制为0 rad)、电阻率相位ϕρ、频率偏量相位ϕ∆f相关,还与发射线圈和接收线圈的位置变化引起的几何相位ϕg、仪器系统的接收电路引入的相位ϕc和数据处理时产生的相位ϕd相关.对于一维地下水探测,发射和接收线圈共线,ϕg可以忽略.而且,采用相同的仪器和数据处理方法,ϕc和ϕd为固定的常数ϕs=ϕc+ϕd,统称为系统相位.因此,接收信号V的相位可以表示为

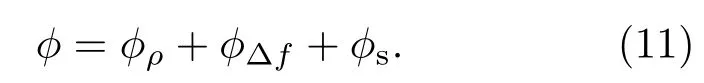
复包络反演的核心是利用表达式(10)中接收信号V(q,t)的实部和虚部,根据已知的ρ和∆f,正演建模计算K,然后通过自动搜索匹配未知的ϕs,多次迭代实现反演模型计算数据与实测数据相互吻合.

复包络反演算法的示意图见图3,V的实部和虚部组成测量数据d矩阵：

其中,dq,p是第q个脉冲矩、第p个时刻的接收信号V(q,tp),R代表信号实部,I代表信号虚部,Q代表q的个数,P代表时间序列个数,H代表转置.

CEI的变量为每层地下水的含水量w和(简写为T),组成变量矩阵m:

其中,wn代表第n层的w,Tn代表第n层的N代表地下分层数.

根据表达式(9)和(10),假设地下ρ分布和∆f已知,正演获得当不存在ϕs时,d=Kw;当存在ϕs且未知时,可以先通过搜索(G(·)为模型正演算子,m0为变量初值)获得初步的相位估计然后,更新的核函数

采用迭代方法计算反演变量mk+1=mk+∆mk.利用表达式(10)分别计算V对w和两个变量的导数(Jacobian)矩阵：

和

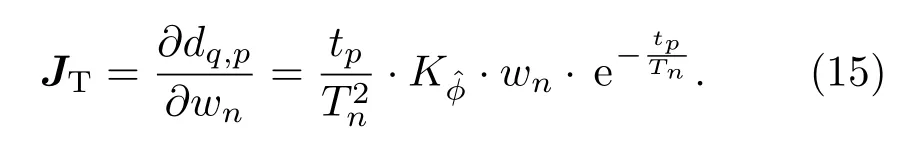
为了将数据的实部和虚部同时参与反演,将Jacobian矩阵整理成：

为了将变量m限制在合理范围内(0＜w＜100%,0＜T∗2＜1 s),利用tan函数将约束空间转换成非约束空间,同时更新J[16].本文采用基于约束加权和先验的共轭梯度最小二乘(CGLSCDP)算法[23,24]进行模型增量∆m求解：

其中,Dε是观测数据的噪声估计加权矩阵,C是模型平滑度矩阵,λ是正则化参数,可利用χ2分布检验或L曲线优化选取[25].

在每次迭代过程中,需要选择最优的迭代步长ηk以防止模型发散：

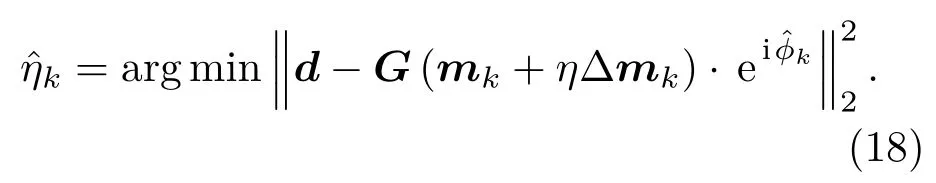
当确定最优步长ˆηk后,重新搜索匹配相位ˆϕk+1,用于确定下一次迭代的相位偏差：

通过多次迭代后,m和ˆϕ均趋于稳定,由反演模型计算数据与测量数据和噪声数据的加权均方差χ2趋近于1时,最终获得反演结果.

图3 复包络反演算法示意图Fig.3.Schematic of complex envelop inversion algorithm.

4 仿真模型结果

4.1 SNMOR信号

为了分析∆f对SNMOR信号的影响,建立包含三个含水层的仿真模型,厚度均为25 m,如图4(a)和图4(b)所示;第一层深度为0—25 m,含水量为5%,T2∗为100 ms,对应细砂层;第二层深度为25—50 m,含水量为25%,T2∗为200 ms,对应粗砂层;第三层深度为50—75 m,含水量为10%,T2∗为50 ms,对应黏土层.SNMOR正演参数与图2中计算K的参数一致.

利用正演表达式(9)和(10)分别计算∆f=±10 Hz范围内的信号V0,即t=0 s时刻的信号幅度,如图4(c)—(e)所示.图4(c)是V0的幅度,当q＜2 As时,∆f对V0的幅度值影响较小(＜7.5%);当q＞2 As时,∆f对V0的幅度值影响逐渐增大.具体表现为SNMR时,V0最小(绿色曲线);SNMOR情况下,随着∆f变化到±10 Hz,V0也逐渐增大(蓝色系和红色系曲线),最大增加了65.9%.说明对于较大的q,SNMOR与SNMR信号幅度明显不同,因此不能忽略∆f的影响.由图4(d)和图4(e)得到,当∆f由0 Hz变化到±10 Hz时,V0的实部逐渐减小,而V0的虚部逐渐增大,但是对于正∆f(红色系曲线)和负∆f(蓝色系曲线),V0虚部的符号相反.因此,∆f既影响FID信号的幅度,也影响其相位,与图2中K的结果一致.

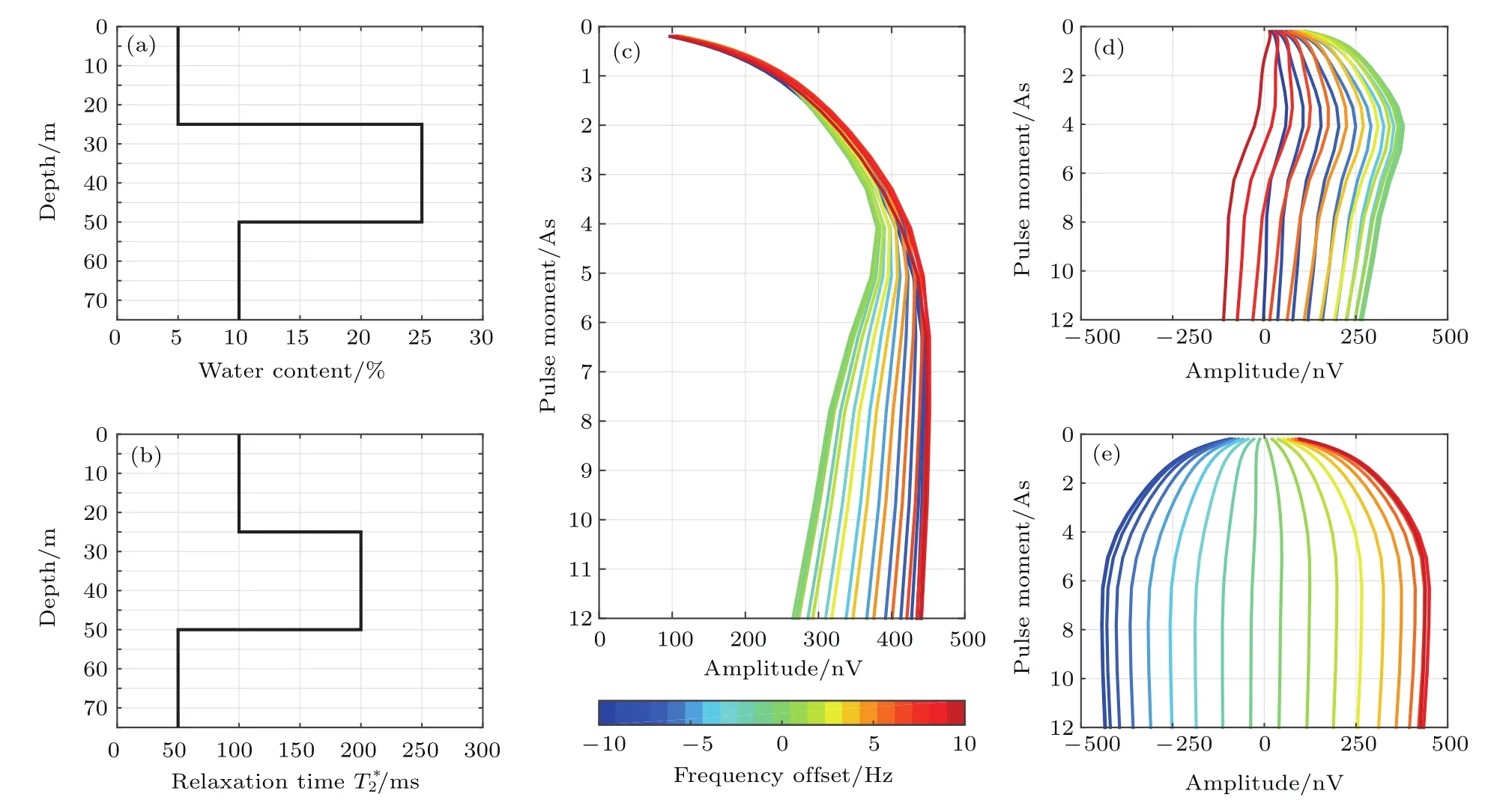
图4 SNMOR仿真模型和正演计算信号的初始振幅V0(a)仿真模型含水量;(b)仿真模型T∗2;(c)正演计算信号V0的幅度;(d)V0的实部;(e)V0的虚部Fig.4.Simulated SNMOR model and forward calculation of the initial values V0of the signal:(a)Water content of model;(b)T∗2of model;(c)amplitude of V0;(d)real part of V0;(e)imagery part of V0.

4.2 SNMOR反演结果

对于图4中的仿真模型和SNMOR信号(模型参数见2.2小节),利用第3节的CEI,获得含水量和T∗2分布结果如图5所示.为了仿真野外环境,在SNMOR信号中加入了50 nV高斯分布的随机噪声,并将FID信号进行了抽道,抽道数为30.在反演过程中,假设初始模型为同一含水层,含水量和T∗2分别为10%和100 ms,最大值分别设定为50%和350 ms,正则化参数选择为1000,经过50次迭代后,所有的反演数据与仿真数据的误差统计χ2≈1.

在复包络反演中,利用了SNMR核函数和SNMOR核函数进行了对比.通常,在地磁场测量不准确或者分布不均匀时,只能假设为SNMR情况,即忽略∆f的影响.由图5(a)和图5(c)中的含水量和T∗2反演结果可知,假设SNMR情况时,∆f的变化对于第一层含水层影响较小,这是因为小脉冲矩时FID信号随∆f变化较小,可以忽略.但是对于第二层和第三层含水层,∆f的影响较大.当∆f＜0 Hz时(蓝色系曲线),第二层含水层的反演结果出现先偏小后偏大的趋势,含水量最大偏差18.4%,T∗2最大偏差56.1 ms.当∆f＞0 Hz时(红色系曲线),第二层和第三层含水层的反演结果出现先偏大后偏小再偏大的振荡趋势,含水量最大偏差36.1%,T∗2最大偏差275.6 ms.由此可以得到,对于较大脉冲矩,FID信号随∆f变化大,对中部和深部含水层的反演结果影响也较大.因此,为了准确探测中部和深部的含水层,不能忽略偏共振的影响.

当准确获得∆f时,可以计算SNMOR核函数应用到复包络反演中,见图5(b)和图5(d).当∆f从−10 Hz变化到10 Hz时,对于第一层和第二层含水层,反演获得的含水量和T∗2分布均与仿真模型基本一致,只在层边界处由于平滑过渡的假设出现缓慢变化;对于第三层含水层,随着∆f不同,反演结果与仿真模型稍有不同,其中含水量最大偏差4.2%,T∗2最大偏差39.3 ms.第三层出现的偏差是因为随深度增加,反演分辨率下降,尤其对于大于50 m的反演结果,分辨率较低.对比SNMR核函数和SNMOR核函数的复包络反演结果得到结论,当频率偏量∆f存在时,利用∆f计算的SNMOR核函数进行反演,可以显著减小∆f对含水量和T∗2反演结果的影响.

图5 不同∆f情况下的复包络反演结果 (a)SNMR核函数反演的含水量;(b)SNMOR核函数反演的含水量;(c)SNMR核函数反演的T∗2;(d)SNMOR核函数反演的T∗2Fig.5.Inversion results with different ∆f:(a)Water content using SNMR kernel;(b)water content using SNMOR kernel;(c)T∗2using SNMR kernel;(d)T∗2using SNMOR kernel.

4.3 CEI与QTI对比

为了对比CEI与QTI的结果,利用图5中的仿真模型和当∆f=3 Hz时的正演FID信号,分别加入噪声水平为50—500 nV高斯分布的随机噪声,进行反演对比实验,反演结果如图6所示.

两种反演方法都利用∆f=3 Hz时的SNMOR核函数K,但是QTI方法计算核函数的模|K|,只有信号幅度参与计算,随着噪声水平增加,含水量和T∗2出现偏差,如图6(a)和图6(c)所示.对于第一层含水层,随着噪声水平增加,QTI结果在浅层出现了较大偏差,含水量和T∗2最大偏差分别为19.9%和177.8 ms.第二层含水层,含水量随着噪声增大先减小后增大,T∗2随噪声增大而增大.对于第三层含水层,含水量和T∗2均随着噪声增大而增大,最大偏差分别为14.1%和205.0 ms.QTI结果说明,随着噪声增加,模型分辨率降低,尤其是噪声较大时(＞300 nV),QTI不能区分第二层和第三层含水层.相比之下,CEI同时利用核函数和信号的实部和虚部,结果更加稳定和可靠.对于不同噪声情况,在第一层含水层中均未出现假含水层,含水量和T∗2最大偏差分别为1.8%和53.3 ms;第二层和第三层的含水量和T∗2分布均比QTI结果的偏差小,说明CEI的模型分辨率优于QTI.因此可以证明,在噪声较小时,CEI和QTI结果无明显差别;随着噪声增加,CEI的优势逐渐明显.但是当噪声很大时,两者的反演结果均不能反映仿真模型.

图6 不同噪声水平的CEI和QTI结果对比(∆f=3 Hz)(a)QTI的含水量;(b)CEI的含水量;(c)QTI的T2∗;(d)CEI的T2∗Fig.6. Results of CEI and QTI with different noise levels(∆f=3 Hz):(a)Water content using QTI;(b)water content using CEI;(c)T2∗using QTI;(d)T2∗using CEI.

5 野外实测数据

为了验证SNMOR探测的有效性,利用JLMRS型地下水探测仪器在长春市郊的太平池水库旁进行了野外实验.该地点的环境噪声较低,实验环境较好,在此进行过多次SNMR和其他方法测量,并且有钻孔资料进行对比验证.综合已知资料得到地下水分布为:1)0—13 m,黏土层,平均含水量为2%;2)13—25 m,细砂和砂砾互层,平均含水量12%;3)25—45 m,黏土层,平均含水量为4%;4)45—62 m,细砂和粘土互层,平均含水量7%.测量地点的平均B0为54720 nT,在一天内变化小于12 nT,对应fT为2330 Hz±0.5 Hz,I为62.11°,测量地下ρ电阻率平均为30 Ωm.SNMOR测量采用边长为50 m的单匝正方形线圈,q为20个,在0.5—10 As之间按照对数分布,每组q下重复测量32次,获得噪声水平平均为11 nV.图7给出了在q=2.4 As时,实测FID信号实部和虚部随∆f变化的曲线,其中蓝色曲线是实测数据,红色曲线是拟合结果,表1总结了实测数据的拟合结果和不确定度.

由图7和表1可以得到:在SNMR情况(∆f=0 Hz)下,实测信号的实部和虚部均按照指数规律单调变化,T∗2为107.2 ms,∆f为0.13 Hz,可以忽略其影响. 在SNMOR情况下(∆f=0 Hz),随着∆f的增加,实测信号的实部和虚部曲线均出现振荡波动,其波动频率与∆f基本一致.在表1中,当∆f从±1 Hz变化到±7 Hz时,V0逐渐增大,最大值比SNMR时增加了52.6%,T∗2基本保持不变(95.5—102.6 ms),环境噪声水平εn不变(9.3—13.6 nV).虽然曲线拟合的初始相位ϕ0结果变化不规律,但是经过后续复CEI后可以获得对应的系统相位ϕs,两者的相位差∆ϕ呈现明显的规律(如表1所列),即随着∆f的增加,∆ϕ也逐渐增加.由以上分析可以证明,当fT与fL出现偏差时,发生SNMOR现象,现有的JLMRS型仪器即可采集到有效的SNMOR信号.而且,SNMOR信号的幅度大于SNMR信号幅度,与理论计算结果相符.

图7 太平池水库野外实测FID信号 (a)共振激发,∆f=0 Hz;(b)偏共振激发,∆f=1 Hz;(c)∆f=−1 Hz;(d)∆f=3 Hz;(e)∆f=−3 Hz;(f)∆f=5 Hz;(g)∆f=−5 Hz;(h)∆f=7 Hz;(i)∆f=−7 HzFig.7. FID signal measured in Taipingchi Reservoir:(a)On-resonance excitation,∆f=0 Hz;(b)off-resonance excitation,∆f=1 Hz;(c)∆f= −1 Hz;(d)∆f=3 Hz;(e)∆f= −3 Hz;(f)∆f=5 Hz;(g)∆f=−5 Hz;(h)∆f=7 Hz;(i)∆f=−7 Hz.

表1 实测FID信号数据拟合结果和不确定度(q=2.4 As)Table 1.Fitted parameters and uncertainty of the fi eld measured FID signals(q=2.4 As).

对于20组q下不同∆f的SNMOR探测结果如图8所示.其中图8(a)是实测FID信号V0的幅度,图8(b)和图8(c)分别是经过系统相位ϕs修正后V0的实部和虚部.图8中的曲线随∆f变化的变化规律与图4仿真结果的规律类似.对于图8(a)中V0的幅度,SNMR时(绿色曲线)相对较小;而SNMOR时,随着∆f增加(蓝色系和红色系曲线),大脉冲矩(q＞2 As)对应的V0幅度逐渐增大.对于图8(b)中的V0实部,SNMR时(绿色曲线)最大,而SNMOR时(蓝色系和红色系曲线)稍有下降.但是,对于图8(c)中的V0虚部,SNMR时(绿色曲线)在0 nV左右,只有q＞7 As时,由于ρ的影响,略有增大.而在SNMOR时(蓝色系和红色系曲线),随着正∆f和负∆f变大,V0虚部的数值均逐渐增加,且符号相反.因此,由实测结果可以证明本文建立的SNMOR正演模型是正确的.

图8 实测FID信号初始振幅V0随∆f的变化曲线 (a)V0的幅度;(b)V0的实部;(c)V0的虚部Fig.8.Initial value V0of the FID signals:(a)The amplitude of V0;(b)the real part of V0;(c)the imagery part of V0.

利用本文提出的CEI,对不同∆f的SNMOR实测数据进行反演得到结果如图9所示.在反演过程中,假设初始模型为同一含水层,含水量为5%,T∗2为100 ms,设定两者的最大值分别为15%和300 ms,正则化参数根据χ分布检验选择,经过50次迭代,得到最终的数据误差统计χ2≈1.图9(a)和图9(c)是不考虑∆f的情况下,假设均采用SNMR核函数时的反演结果,可以得到只有当fT和fL近似相等时(绿色曲线),反演结果的含水量和T∗2与已知资料相近,当频率不相等时,反演误差较大,如在浅层(＜5 m处)出现假含水层(蓝色系曲线),对于第二层和第四层的含水量偏低,第三层含水量偏高(红色系曲线)等.随着∆f增大,反演结果的误差也随之增大,当∆f=±7 Hz时已经不能反映地下含水层的真实分布情况.图9(b)和图9(d)是采用∆f计算的SNMOR核函数的反演结果,与共振情况相比,含水量和T∗2分布能够正确反演地下含水层分布情况.但是,随着频率偏量的增加,反演结果的误差也逐渐增大,尤其是对于∆f=±7 Hz的蓝色系和红色系曲线,第二层和第三层的含水量和T∗2的误差较大,只能近似反映真实情况.因此,通过实测数据反演结果可以证明,SNMOR现象发生时,需要准确获得∆f,通过CEI才能获得更准确的地下含水层分布.

图9 不同∆f时实测FID信号的CEI结果 (a)SNMR核函数反演的含水量;(b)SNMOR核函数反演的含水量;(c)SNMR核函数反演的T∗2;(d)SNMOR核函数反演的T∗2Fig.9.Inversion results of the fi eld measured FID signals with different∆f:(a)Water content using SNMR kernel;(b)water content using SNMOR kernel;(c)T∗2using SNMR kernel;(d)T∗2using SNMOR kernel.

最后,利用不同噪声水平下的实测数据对比反演结果,验证CEI的优势.噪声水平与叠加次数相关,32次、24次、16次和4次叠加数据分别获得的噪声水平为11,15,21和26 nV,由此可以获得不同噪声水平实测数据的反演结果,如图10所示.图10(a)和(c)是利用∆f=3 Hz的核函数进行QTI的结果,可见随着噪声增大,反演结果逐渐偏离真实模型.当噪声为11 nV时,除了T2∗显示出浅层的假含水层以外,其他结果与真实模型类似,但是当噪声增大到20 nV以上后,含水量和T2∗大幅度偏离了真实模型.图10(b)和图10(d)利用∆f=3 Hz的核函数进行CEI的结果,当噪声增大时,反演结果基本与真实模型一致,只有第四个含水层由于噪声增加,分辨率下降,因此含水量和T2∗逐渐偏小.由CEI和QTI的结果对比可以得到结论,在较大噪声环境下,CEI充分利用数据的有用信息,能够获得比QTI更稳定和可靠的结果.

6 结 论

SNMR方法是目前唯一一种直接探测地下水的地球物理方法.由于地磁场不均匀性,时变性和易受干扰等问题影响,在实际测量中经常进行SNMOR探测.本文针对SNMOR中偏共振激发引起FID信号的幅度和相位变化,提出包络信号实部和虚部同时参与的CEI,通过自动搜索方案估计未知的系统相位,实现了SNMOR探测中含水量和弛豫时间(T∗2)的准确反演.最后,通过仿真模型和实测数据验证了SNMOR正演模型和CEI的有效性和准确性.

图10 不同噪声水平的CEI和QTI结果对比(∆f=3 Hz) (a)QTI的含水量;(b)CEI的含水量;(c)QTI的T∗2;(d)CEI的T∗2Fig.10. Results of CEI and QTI with different noise levels(∆f=3 Hz):(a)Water content using QTI;(b)water content using CEI;(c)T∗2using QTI;(d)T∗2using CEI.

在SNMOR探测中,随着频率偏量的增加,FID信号初始振幅的实部稍有减小,而虚部的数值逐渐增加,其符号与频率偏量的符号一致,说明信号相位受频率偏量的影响较大.在本文的仿真模型中,信号幅度随频率偏量增加而增大,最大增幅达到65.9%.常规反演不考虑频率偏量的影响,只利用SNMR核函数,因此含水量和T∗2的反演结果误差较大.本文根据频率偏量准确计算了SNMOR核函数,利用CEI方法提高了含水量和T∗2反演结果的准确度,在仿真模型中最大偏差为4.2%和39.3 ms.通过与QTI方法进行对比得到,CEI充分利用测量数据的全部信息,反演结果优于QTI,当噪声较大时,仍然能够获得更稳定和可靠的反演结果.

本文通过SNMOR探测中实测FID信号的拟合结果获得频率偏量,可以修改发射频率重新测量以保证共振激发,也可以利用本文提出的偏共振模型和CEI反演方法直接获得准确的地下水文信息.但是,如果频率偏量较大,超过了交变磁场引起的章动频率,将会导致无法有效激发氢质子,从而造成较大的测量误差.此时,必须调整发射频率使其等于或接近Larmor频率.另外,在测量过程中,有时频率偏量也存在随时间和空间变化,或者强噪声影响测量结果.因此,需要进一步研究频率偏量变化时的SNMOR反演问题,以及利用频率环等测量序列解决Larmor频率未知时的探测问题.

[1]Legtchenko A 2013Magnetic Resonance Imaging for Groundwater(Hoboken:John Wiley&Sons)p10

[2]Li X,Xiao L Z,Liu H B,Zhang Z F,Guo B X,Yu H J,Zong F R 2013Acta Phys.Sin.62 147602(in Chinese)[李新,肖立志,刘化冰,张宗富,郭葆鑫,于慧俊,宗芳荣2013物理学报62 147602]

[3]Behroozmand A A,Keating K,Auken E 2015Surv.Geophys.36 27

[4]Hertrich M 2008Prog.Nucl.Mag.Res.Sp.53 227

[5]Hürlimann M D 1998J.Mag.Res.131 232

[6]Chen Q,Marble A E,Colpitts B G,Balcom B J 2005J.Mag.Res.175 300

[7]Grunewald E,Knight R 2012Geophysics77 EN1

[8]Legchenko A,Vouillamoz J M,Lawson F M A,Alle C,Descloitres M,Boucher M 2016Geophysics81 WB23

[9]Legchenko A,Vouillamoz J M,Roy J 2010Geophysics75 L91

[10]Lin J,Jiang C D,Lin T T,Duan Q M,Wang Y J,Shang X L,Fan T H,Sun S Q,Tian B F,Zhao J,Qin S W 2013Chin.J.Geophys.56 3619(in Chinese)[林君, 蒋川东,林婷婷,段清明,王应吉,尚新磊,范铁虎,孙淑琴,田宝凤,赵静,秦胜武2013地球物理学报56 3619]

[11]Walbrecker J O,Hertrich M,Green A G 2011Geophysics76 G1

[12]Grombacher D,Walbrecker J O,Knight R 2014Geophysics79 E329

[13]Irons T P,Li Y 2014Geophys.J.Int.199 1372

[14]Grombacher D,Knight R 2015Geophysics80 E329

[15]Grombacher D,Müller-Petke M,Knight R 2016Geophysics81 WB33

[16]Mueller-Petke M,Yaramanci U 2010Geophysics75 WA199

[17]Roy J,Lubczynski M W 2014Near Surf.Geophys.12 309

[18]Chen B,Hu X,Li J,Liu Y 2016Groundwater55 171

[19]Weichman P B,Lavely E M,Ritzwoller M H 2000Phys.Rev.E62 1290

[20]Lehmann-Horn J A,Hertrich M,Greenhalgh S A,Green A G 2011IEEE Trans.Geosci.Remote.Sens.49 3878

[21]Bloch F 1946Phys.Rev.70 460

[22]Jiang C D,Lin J,Duan Q M,Tian B F,Hao H C 2011Chin.J.Geophys.54 2973(in Chinese)[蒋川东,林君,段清明,田宝凤,郝荟萃2011地球物理学报54 2973]

[23]Walbrecker J O,Hertrich M,Green A G 2009Geophysics74 G27

[24]Günther T,Rücker C,Spitzer K 2006Geophys.J.Int.166 506

[25]Jiang C,Liu J,Tian B,Sun S,Lin J,Müller-Petke M 2016Geophysics81 E363