相对论多组态相互作用方法计算Mg+离子同位素位移∗

余庚华 颜辉 高当丽 赵朋义 刘鸿 朱晓玲 杨维

1)(成都大学信息科学与工程学院,成都 610106)

2)(华南师范大学,广东省量子调控工程与材料重点实验室,广州 510006)

3)(西安建筑科技大学理学院,西安 710055)

4)(湖北师范大学物理与电子科学学院,黄石 435002)

1 引 言

同位素位移(isotope shift,IS)的理论和实验研究应用广泛,是基础物理研究的热点内容之一[1−3].IS是研究原子核性质的有效手段之一,通过测量IS可以获得核电荷半径、磁偶极矩、电四极矩、核自旋和超精细结构等重要的原子数据[4−7];在基础物理领域,IS可以用于检验量子力学计算方法和标准模型理论,研究精细结构常数α的时空演化性质[8−10];在天体物理的研究中,IS可以用于研究黑洞的性质和霍金辐射[11−13].此外,IS的应用还包括原子分子精密谱、光频标、冷原子物理和原子的激光冷却与囚禁等方面[14−17].对绝大多数元素而言,可供参考的IS实验数据很少,更多的时候需要进行理论计算.因此,在准确计算IS方面取得的任何进展都显得特别有意义.近年来,Mg元素(核电荷数Z=12)的IS效应研究一直受到关注[18−20].和测量类星体(quasars and quasi-stellar object,QSO)的C同位素(核电荷数Z=6)吸收丰度来检验宇宙的化学演化模型类似[21],在一些的化学演化模型中,大量的中等质量恒星会产出Mg同位素,研究这些恒星中Mg同位素的相对丰度变化可以为恒星演化提供相应的直接证据[22].同时,Mg的同位素很多,半衰期在在几十毫秒至几十小时的同位素有十几个,其中包括幻中子数N=8,18和28的同位素,这些短寿命同位素是研究反转岛附近原子核奇特性质的重要对象[23,24],通过研究这些同位素的IS可以帮助我们获得相应的奇异原子核的重要性质.

图1 Mg+离子基态和低激发态能级图Fig.1.The diagram of ground and low lying energy levels of Mg+ion.

我们选择Mg+离子基态到低激发态3s2S1/2—3s2P1/2和 3s2S1/2—3s2P3/2两条跃迁谱线作为研究对象,计算其同位素位移.跃迁能级如图1所示,这两条跃迁对应的波长分别为280.3和279.6 nm.原子谱线的IS包括两方面的贡献,原子核的有限质量引起的质量位移(mass shift,MS)和原子核的电荷分布引起的场位移( fi eld shift,FS).质量位移又可分为正常质量位移(normal mass shift,NMS)和特殊质量位移(speci fi c mass shift,SMS).理论计算IS的难点主要在于SMS和FS,常用的处理方式有组态相互作用(con fi guration interaction,CI)、多体微扰论(many-body perturbation theory,MBPT)、耦合簇方法、Dirac-Fock-Sturm(DFS)方法以及Dirac-Hartree-Fock(DHF)方法等,由此发展起来的CI+MBPT[25−27]、相对论耦合簇[28],CI+DFS[29,30]和多组态DHF(multi-con fi guration Dirac-Hartree-Fock method,MCDHF)[31−33]等计算方法在IS的理论研究中取得了比较好的结果.

在Mg+离子的IS计算中采用MCDHF方法,结合相对论组态相互作用(relativistic con fi guration interaction,RCI)和自洽场(self-consistent fi eld,SCF)方法对电子波函数用进行优化,并在RCI计算中引入Breit近似,得到了Mg+离子3s2S1/2—3s2P1/2和 3s2S1/2—3s2P3/2两条跃迁谱线的SMS系数和FS因子,并计算了中子数8≤N≤20的Mg+离子同位素位移.用RCI和MCDHF方法计算Mg+离子IS的理论结果与用其他理论方法得到的计算结果符合得比较好,与最新的Mg+离子IS测量实验结果相比也符合得很好.

2 理论方法

2.1 同位素位移一般理论

考虑能级为l和u之间的一条原子跃迁谱线,能级l和u对应的能量分别为Eu和El(Eu＞El),原子谱线跃迁频率为v;两个同位素对应的质量数分别为A和A′;则能级l和u之间跃迁hv=Eu−El的IS可以表示为[19,32,33]:

其中,δvA,A′是该原子跃迁谱线的IS;∆KNMS,∆KSMS和F分别为NMS系数、SMS系数和FS因子;M和M′分别是同位素A和A′对应的原子核质量,δ〈r2〉A,A′是同位素A和A′原子核方均根电荷半径的平方差.

NMS系数可以表示为

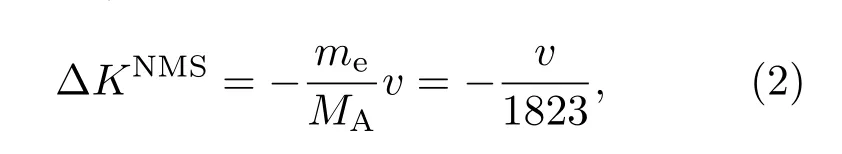
其中me是电子质量,MA是单位原子质量,1823是单位原子质量与电子质量的比值.引入SMS算符:

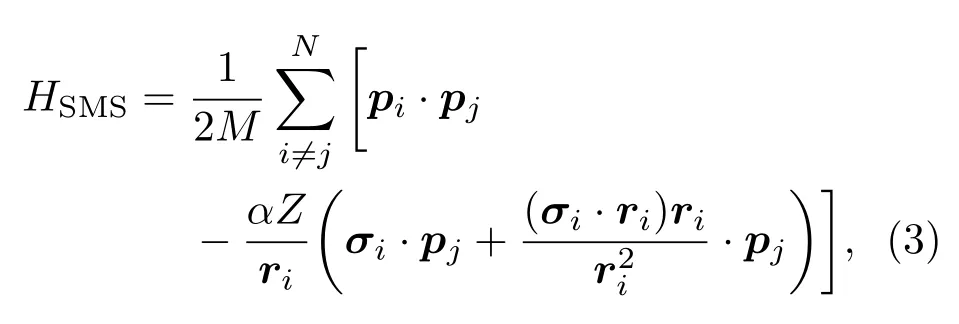
其中Z为核电荷数,α为精细结构常数,σi是(4×4)狄拉克矩阵.

设能级i(i=l,u)对应的电子波函数为|Ψi〉,则该能级的SMS系数表示为

于是,能级l和u之间跃迁的SMS系数可以表示为

场位移因子F正比于原点r=0处的电子概率幅密度的变化:

其中,ρei(0)(i=l,u)是原点r=0处的电子电荷密度.

用上述公式可以分别计算NMS,SMS和FS的贡献,三者相加即是总的IS.

2.2 MCDHF和RCI数值计算方法

在 MCDHF方法中,原子态波函数(atomic state wave function,ASF)可以表示成组态函数(con fi guration state function,CSF)的线性叠加[31−33]:

其中,P为宇称,J是角动量量子数,MJ是角动量J的z分量,{cµ}是叠加系数,{γµ}是标识CSFs的一组量子数.叠加系数{cµ}和CSFs通过SCF方法进行同步优化.用RCI方法开展计算时,将Breit相互作用作为微绕项进行考虑.

我们用GRASP2K原子结构计算程序包[31]和RIS3同位素位移计算程序包[33]来开展计算.GRASP2 K程序包可以系统地计算电子关联效应,包括价电子和内层电子之间的关联以及原子核与核外电子之间的关联等.对于中性原子和近似中性的离子而言,电子关联效应是理论计算和实验测量之间差异的主要来源.用GRASP2K程序包先计算ASFs,再用RIS3程序包调用ASFs来计算同位素位移.

在GRASP2 K程序包中采用了双参数费米模型来描述原子核的电荷分布.双参数费米模型如下[34]:

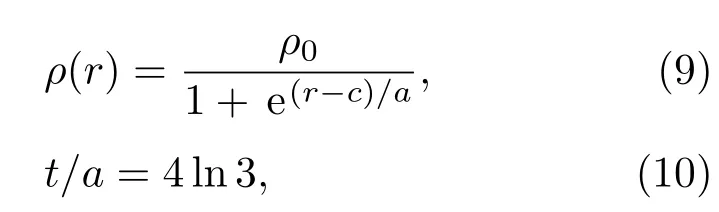
其中ρ0是归一化系数,c为半密度半径,t为原子核皮厚度,a是与核皮厚度t相关的参数,t取值为2.30 fm.

2.3 原子核质量修正

原子核的质量可以用原子质量进行修正得到,方法为:原子质量扣除电子质量,再加上电子与核的结合能:

其中Bel是电子与核的结合能,它可以由下列经验公式进行估算[35]:

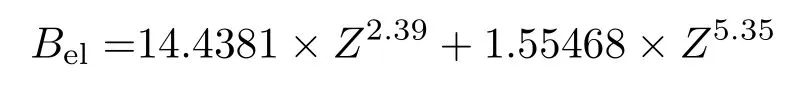
进行原子核质量修正时注意需要将能量单位eV换算成原子质量单位amu.

3 计算结果

Mg+离子的基态电子组态为1s22s22p63s1,计算过程中展开CSFs时采用的是一种受限制的双电子激发模式:最里层1s2的两个电子选择不激发,最外层3s1中的一个电子选择激发,另从2s22p6八个电子中再选择一个电子激发.CSFs对应的主量子数n=3,4,5,···,轨道角量子数l=0,1,2,3,···,n−1(对应的光谱学符号表示为l=s,p,d,f,···),计算中最大的主量子数为nmax=6,最大的轨道角量子数lmax=4(用光谱学符号表示为lmax=g).

3.1 谱线的跃迁能量

在计算电子波函数的同时也得到了Mg+离子基态到低激发态3s2S1/2—3s2P1/2和3s2S1/2—3s2P3/2两条谱线的跃迁能量,以波数(cm−1)为单位,并与实验值和其他理论值[28]进行了对比,结果如表1所列.实验值取自美国国家标准研究院(The National Institute of Standards and Technology,NIST)的原子光谱数据库(atomic spectra database,ASD).表1中括号里的百分数表示的是理论计算结果与NIST ASD的实验数据为参考的相对百分差.其中,文献[28]采用的是相对论耦合簇计算方法,本文计算的两条谱线的跃迁能量与实验和理论都符合得比较好,表明本文对电子波函数的计算准确可靠.

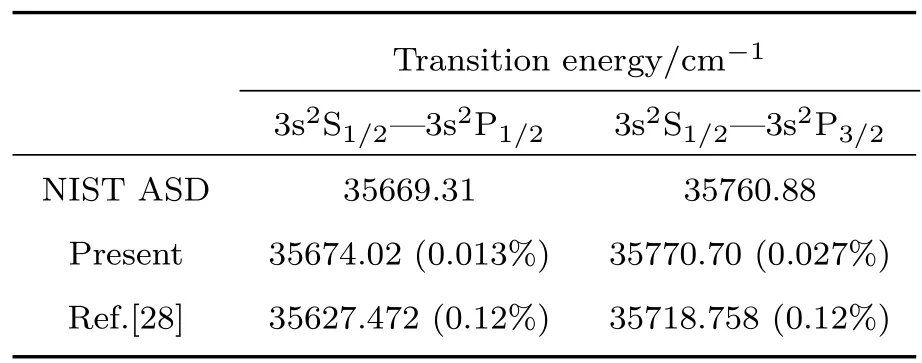
表1 Mg+离子3s2S1/2—3s2P1/2 和 3s2S1/2—3s2P3/2谱线跃迁能量,括号中的百分数表示与NIST ASD实验测量值的相对百分差Table 1.Transition energies for 3s2S1/2–3s2P1/2and 3s2S1/2–3s2P3/2transitions of Mg+ion.The data in brackets represents the percentage difference compared with the NIST ASD result.

3.2 特殊质量位移系数和场位移因子

Mg+离子3s2S1/2—3s2P1/2和3s2S1/2—3s2P3/2两条跃迁谱线的NMS系数、SMS系数和FS因子的计算结果如表2所列,NMS系数和SMS系数的单位为 GHz·amu,FS因子的单位为 MHz·fm−2. 表中比较了CI+MBPT方法[19,25]、相对论耦合簇方法[28]、相对论HF方法[36]以及相对论CI+DF方法[37]的计算结果.其中,文献[19]是在有限场近似下将SMS算符作为一个微绕项加入到系统的哈密顿量中再用CI+MBPT方法展开计算;文献[25]采用的也是CI+MBPT方法,但在计算跃迁矩阵元高阶修正时采用了随机相位近似(random-phase approximation);文献[28]中采用Dirac哈密顿量结合Breit近似计算电子波函数,但是在计算SMS系数时用的是非相对论形式的SMS算符;文献[36]是将同位素位移算子加入到库仑势中,这种处理方式与文献[19]很相似,因此二者对场位移因子F的计算结果相同,且SMS系数的计算结果也很接近;文献[37]用CI+DF方法展开求解组态波函数时引入了一个权重函数(weight function),但是没有详细考虑电子的关联效应.表2中不同的计算方法各有特色,计算得到的SMS系数和场位移因子虽然存在一些差异,但是总的来看,这些理论结果彼此都还符合得比较好.

表2 Mg+离子3s2S1/2—3s2P1/2和 3s2S1/2—3s2P3/2跃迁谱线的NMS系数、SMS系数和FS因子(NMS和SMS系数的单位为GHz·amu,场位移因子 F 的单位为MHz·fm−2)Table 2.The NMS coefficients,SMS coefficients and FS factors for the 3s2S1/2–3s2P1/2and 3s2S1/2–3s2P3/2 transitions of Mg+ion.The unit of the NMS and SMS coefficient is GHz·amu and the unit of the fi eld shift factor F is MHz·fm−2.

用表2中NMS系数、SMS系数和FS因子的计算结果结合必要的原子核质量和核电荷半径数据,就可以计算相应的Mg+离子这两条跃迁谱线的IS,并与实验结果进行对比.

3.3 同位素位移

Mg元素稳定的同位素有三个,24Mg,25Mg和26Mg,原子核方均根电荷半径[38]分别为3.0570(7)fm,3.0290(7)fm和3.0340(26)fm,用(11)和(12)式修正后的原子核质量分别为23.9790132016,24.9798084806和25.9765644726 amu.以24Mg+离子为参考同位素,25Mg+离子和26Mg+离子的IS计算结果如表3所列,表3同时列出了其他理论计算值和实验测量值,并与我们的计算结果进行了对比.需要说明的是,最新的Mg+离子稳定同位素的IS实验测量[40]是在离子阱囚禁装置中完成的,在实验中消除了多普勒频移,并对光频移、亚多普勒频移等频移效应做了修正,是目前精度最高的Mg+离子IS实验测量结果.

对于25Mg+离子两条谱线的IS结果,我们的计算值与最新实验测量值[40]的绝对误差分别只有2.1 MHz(3s2S1/2—3s2P1/2)和3.7 MHz(3s2S1/2—3s2P3/2),相对误差分别为0.13%和0.23%,与实验符合得非常好.对26Mg+离子的IS而言,我们计算的SMS和MS与其他理论结果[19,36]的绝对误差在3—6 MHz范围,相对误差小于0.26%;两条谱线总的IS计算结果与实验值[40]的绝对误差分别为6.6 MHz(3s2S1/2—3s2P1/2)和8.9 MHz(3s2S1/2—3s2P3/2),相对误差分别为0.21%和0.28%.与其他理论计算相比,我们对Mg+离子3s2S1/2—3s2P1/2和3s2S1/2−3s2P3/2两条跃迁谱线的IS计算结果最接近实验测量值.

表3 Mg+离子稳定同位素3s2S1/2—3s2P1/2和 3s2S1/2—3s2P3/2跃迁谱线的IS计算结果(参考同位素为24Mg+离子,IS单位为MHz)Table 3.The IS results of the stable Mg+ion isotopes for the 3s2S1/2–3s2P1/2 和 3s2S1/2–3s2P3/2transitions with the unit of MHz.The reference isotope is24Mg+ion.

考虑到中子数8≤N≤20的短寿命Mg同位素在反转岛附近奇异原子核结构性质研究中的重要应用,我们也计算了这些短寿命离子的IS.中子数8≤N≤20的短寿命Mg同位素的原子质量[41]、半衰期、原子核质量修正结果、原子核电荷半径以及核电荷半径的平方差等数据如表4所列,其中参考同位素为24Mg.

结合表2中NMS系数、SMS系数、FS因子的计算结果和表4中各同位素原子核质量和原子核电荷半径数据,以24Mg+离子为参考同位素,得到中子数8≤N≤20的短寿命Mg+离子的IS计算结果如表5所列.

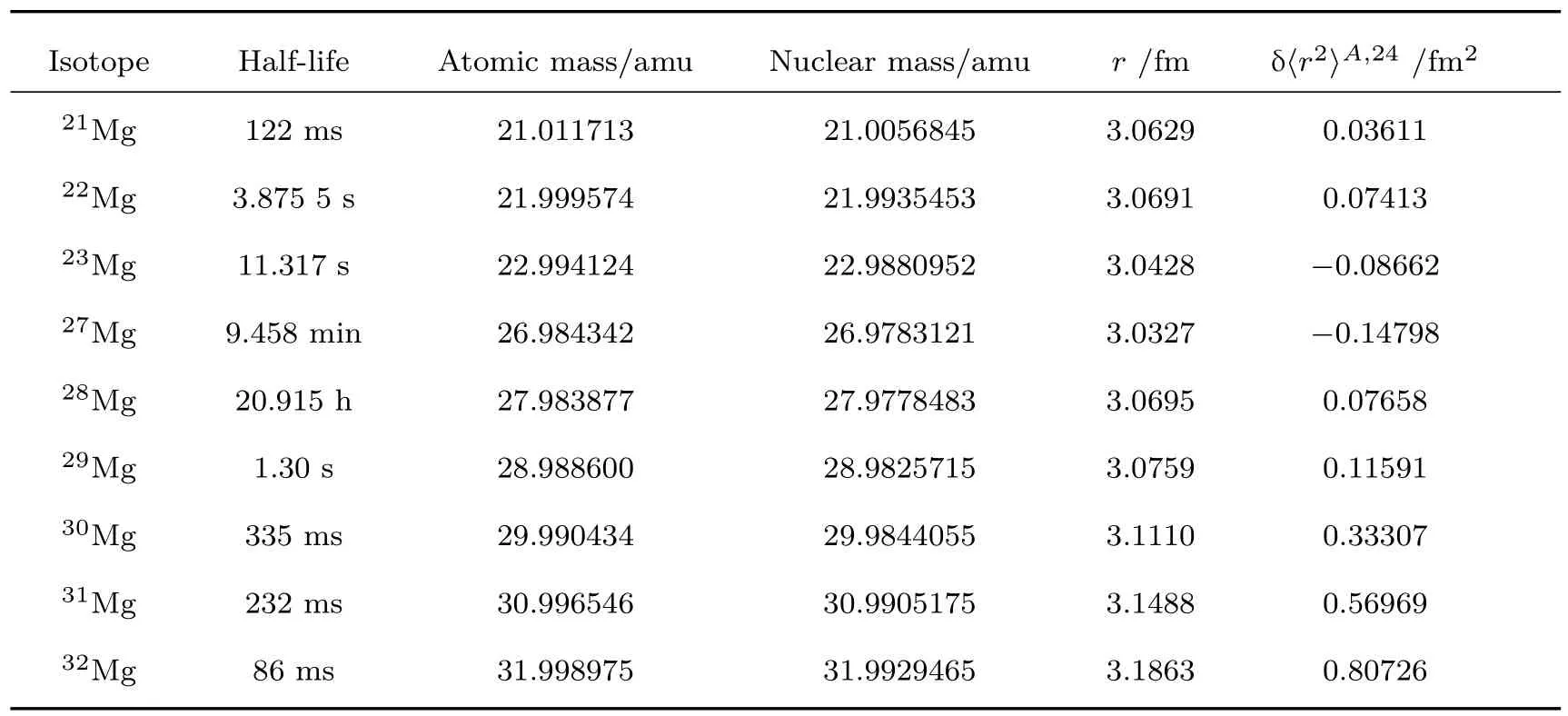
表4 短寿命Mg同位素的原子质量、半衰期、修正后的原子核质量、原子核半径以及原子核半径的平方差,参考同位素为24MgTable 4.The atomic masses(amu),half-lives(in units of h-hour,min-minute,s-second and ms-millisecond),modi fi ed nuclear mass(amu),nuclear charge radius(r,in unit of fm)and the difference of charge radius square(δ〈r2〉,in unit of fm2)for the short-lived Mg isotopes.The reference isotope is24Mg.

表5 短寿命Mg+离子同位素3s2S1/2—3s2P1/2和3s2S1/2—3s2P3/2跃迁谱线的IS计算结果,IS单位为MHz,参考同位素为24Mg+离子Table 5.The IS results of the short-lived Mg+ion isotopes for the 3s2S1/2–3s2P1/2 和 3s2S1/2–3s2P3/2 transitions with the unit of MHz.The reference isotope is24Mg+ion.

表5中IS理论计算结果依赖于原子质量和原子电荷半径的实验数据.原子质量一般能准确到10−7amu量级,原子电荷半径会存在一定的测量误差,但是考虑到对Mg这样的轻核元素而言FS在总IS中的贡献比较小,我们认为IS的计算误差主要来源于NMS系数、SMS系数和FS因子的不确定度.表5的IS理论计算结果的相对不确定度大约为0.30%,评估相对不确定度的依据将在下文讨论.对于中子数8≤N≤20的短寿命Mg+离子同位素3s2S1/2—3s2P1/2和 3s2S1/2—3s2P3/2两条跃迁谱线,目前并没有实验数据可以比对,这些短寿命的同位素半衰期从几十毫秒到几十个小时,足够用于IS测量,且这两条跃迁对应的波长分别为279.6和280.3 nm,这种波长的激光光源也很容易获得,因此表5中的计算结果可以用作进一步的IS测量实验参考.

4 讨 论

在表2中列出了用不同方法计算SMS系数的理论结果,其中文献[28]和[37]的计算结果与其他理论值的差异比较大,主要原因在于:文献[28]中计算电子波函数时用的是相对论狄拉克哈密顿量,但是在计算SMS系数时忽略了SMS算符中相对论效应的近似项;在文献[37]的计算中,未充分考虑电子的关联效应,而电子关联效应在中性原子和近似中性离子的IS中的作用不可忽视.GRASP2K原子结构计算程序包可以对电子关联效应做系统地计算,同时采用了相对论的SMS算符表达式,从而获得了与实验值更接近的计算结果.在计算Mg+离子IS时采用的是受限制的双电子激发模式,且将NMS和SMS分开进行计算;用类似的处理方法也计算了Mg原子的同位素位移[42],并得到了与实验结果相符的计算结果.表明我们采用的受限制的双电子激发模式在处理核外电子数为11和12的原子体系的光谱计算问题是成功的,同时表明将NMS和SMS分别用不同的方法进行处理也是可行的.

GRASP2 K原子结构计算程序包本身没有设计对计算结果进行误差分析的程序模块,因此用GRASP2 K开展理论计算的文献通常只对自身计算结果的不确定度做粗略评估,主要把计算结果与实验测量或者其他理论计算结果进行比较.在IS的计算中,SMS系数和FS因子的不确定度受电子波函数的计算精度影响.从IS的计算方法和GRASP2 K计算程序包的应用特点来看,存在这样的规律:如果跃迁能量与实验值的相对不确定度为∆%,则FS的理论计算值的相对不确定与∆%同量级,而SMS的理论计算值的相对不确定度比∆%要高一个量级,大约为∆%的10倍左右.谱线跃迁能量或者能级能量本质上是哈密顿算符的期望值,其不确定度反映的是电子波函数的计算精度.FS因子正比于两个跃迁能级的电子波函数在原点处的模的平方差(概率幅之差),因此FS只受电子波函数的计算精度影响,与∆%同量级.计算SMS系数引入的相对论SMS算符是在(αZ)4m2/M近似条件下的结果[43,44],所以SMS系数的计算精度不仅受电子波函数的计算精度影响,同时也受近似条件的影响,总的结果是SMS计算的不确定度要比∆%高大约一个量级,可以粗略评估为∆%×10.根据本文的计算结果,两条谱线跃迁能量的相对不确定度最大为0.027%,因此我们评估表5中IS计算结果的不确定度大约为0.30%.

采用MCDHF和RCI方法开展原子结构理论计算的结果与实验值的相对误差通常在1%范围左右,用GRASP2K计算Mg+离子两条谱线的IS理论值与实验测量值的相对误差在0.13%—0.28%范围.为了进一步提高IS的理论计算精度,可以考虑在计算中引入QED(quantum electrodynamics,QED)修正[2,30,45,46].QED修正在少电子体系比如Li原子、Be+离子和Be原子等的IS计算中取得了很大的成功,IS计算精度获得了提高.最新的研究文献表明QED修正也可应用于多电子体系比如碱金属Na,K,Rb,Cs和类碱金属离子的光谱计算[47],说明引入QED修正方法来进一步提高多电子原子体系的IS计算精度是可行的办法.

5 结 论

本文用RCI结合MCDHF方法计算了Mg+离子3s2S1/2—3s2P1/2和 3s2S1/2—3s2P3/2两条跃迁谱线的SMS系数和FS因子,并计算了中子数8≤N≤20的Mg+离子的IS,包括3个稳定同位素和9个短寿命同位素.用GRASP2 K原子结构计算程序包计算电子波函数,并用RIS3同位素位移计算程序包调用GRASP2K的电子波函数计算结果,进而计算IS.本文的计算结果与其他理论计算结果符合得比较好,与最新的实验测量值相比,本文得到的IS理论值的相对误差在0.13%—0.28%范围,是目前最接近IS实验测量值的计算结果.该计算结果能为Mg+离子IS实验和理论研究提供参考,能够用于Mg+离子的短寿命同位素的光谱测量实验以及利用Mg+离子开展幻中子数N=8和N=20附近的奇异原子核特性研究等.同时,本文采用的一种受限制的双电子激发模式对于基态电子组态为1s22s22p63s1的原子体系具有普适性,计算结果也表明这种电子激发模式在计算Mg+离子光谱是可靠的,可以推广到核外电子数为11的多电子体系的原子或离子,比如Na原子、Al2+离子、Si3+离子等,用于开展相应的光谱结构和IS的理论研究.

[1]Volotka A V,Glazov D A,Shabaev V M,Tupitsyn I I,Plunien G 2015Phys.Rev.Lett.112 253004

[2]Yan Z C,Nörtershäuser W,Drake G W F 2008Phys.Rev.Lett.100 243002

[3]Cheal B,Cocolios T E,Fritzsche S 2012Phys.Rev.A86 042501

[4]Borremans D,Balabanski D L,Blaum K,Geithner W,Gheysen S,Himpe P,Kowalska M,Lassen J,Lievens P,Mallion S,Neugart R,Neyens G,Vermeulen N,Yordanov D 2005Phys.Rev.C72 044309

[5]Neugart R,Balabanski D L,Blaum K,Borremans D,Himpe P,Kowalska M,Lievens P,Mallion S,Neyens G,Vermeulen N,Yordanov D T 2008Phys.Rev.Lett.101 132502

[6]Nörtershäuser W,Sánchez R,Ewald G,Dax A,Behr J,Bricault P,Bushaw B A,Dilling J,Dombsky M,Drake G W F,Götte S,Kluge H J,Kühl T,Lassen J,Levy C D P,Pachucki K,Pearson M,Puchalski M,Wojtaszek A,Yan Z C,Zimmermann C 2011Phys.Rev.A83 012516

[7]Takamine A,Wada M,Okada K,Sonoda T,Schury P,Nakamura T,Kanai Y,Kubo T,Katayama I,Ohtani S,Wollnik H,Schuessler H A 2014Phys.Rev.Lett.112 162502

[8]Tang L Y,Yan Z C,Shi T Y,James F B 2009Phys.Rev.A79 062712

[9]DuffM J,Okun L B,Veneziano G 2002J.High Energy Phys.2002 023

[10]Webb J K,King J A,Murphy M T,Flambaum V V,Carswell R F,Bainbridge M B 2011Phys.Rev.Lett.107 191101

[11]Hawking S W 1974Nature248 30

[12]Drobyshevski E M,Drobyshevski M E,Izmodenova T Y,Telnov D S 2003Astron.Astrophys.Trans.22 263

[13]Federman S R,Lambert D L,Cardelli J A,Sheffer Y 1996Nature381 764

[14]Xu P,Yang J W,Liu M,He X D,Zeng Y,Wang K P,Wang J,Papoular D J,Shlyapnikov G V,Zhan M S 2015Nat.Commun.6 7803

[15]Papp S B,Pino J M,Wieman C E 2008Phys.Rev.Lett.101 040402

[16]Burke J P,Bohn J L,Esry B D,Greene C H 1998Phys.Rev.Lett.80 2097

[17]Hamilton M S,Gorges A R,Roberts J 2012J.Phys.B45 095302

[18]Filippin L,Godefroid M,Ekman J,Jönsson P 2016Phys.Rev.A93 062512

[19]Korol V A,Kozlov M G 2007Phys.Rev.A76 022103

[20]Yu G H,Zhao P Y,Xu B M,Zhu X L,Yang W 2017Mod.Phy.Lett.B31 1750003

[21]Fenner Y,Murphy M T,Gibson B K 2005Mon.Not.R.Astron.Soc.358 468

[22]Ashenfelter T P,Mathews G J,Olive K A 2004Phys.Rev.Lett.92 041102

[23]Patra S K,Praharaj C R 1991Phys.Lett.B273 13

[24]Shubhchintak N,Chatterjee R,Shyam R,Tsushima K 2015Nucl.Phys.939 101

[25]Safronova M S,Johnson W R 2001Phys.Rev.A64 052501

[26]Safronova M S,Tupitsyn I I 2015Comput.Phys.Commun.195 199

[27]Dzuba V A,Johnson W R,Safronova M S 2005Phys.Rev.A72 022503

[28]Sahoo B K 2010J.Phys.B43 231001

[29]Kozhedub Y S,Volotka A V,Artemyev A N,Glazov D A,Plunien G,Shabaev V M,Tupitsyn I I,Stöhlker T 2010Phys.Rev.A81 042513

[30]Yan Z C,Drake G W F 2002Phys.Rev.A66 042504

[31]Nazé C,Gaidamauskas E,Gaigalas G,Godefroid M,Jönsson P 2013Comput.Phys.Commun.184 2187

[32]Jönsson P,He X,Fischer C F,Grant I 2007Comput.Phys.Commun.177 597

[33]Jönsson P,Gaigalas G,Bierón J,Fischer C F,Grant I 2013Comput.Phys.Commun.184 2197

[34]Lunney D,Pearson J M,Thibault C 2003Rev.Mod.Phys.75 1021

[35]Wang M,Audi G,Wapstra A H,Kondev F G,Maccormick M,Xu X,Pfeiffer B 2012Chin.Phys.C36 1603

[36]Berengut J C,Dzuba V A,Flambaum V V 2003Phys.Rev.A68 022502

[37]Tupitsyn I I,Shabaev V M,López-Urrutia J R C,Draganic I,Orts R S,Ullrich J 2003Phys.Rev.A68 022511

[38]Yordanov D T,Bissell M L,Blaum K,de Rydt M,Geppert C,Kowalska M,Krämer J,Kreim K,Krieger A,Lievens P,Neff T,Neugart R,Neyens G,Nörtershäuser W,Sánchez R,Vingerhoets P 2012Phys.Rev.Lett.108 042504

[39]Drullinger R,Wineland D,Bergquist J 1980Appl.Phys.22 365

[40]BatteigerV,KnünzS,HerrmannM,Saathoff G,Schüssler H A,Bernhardt B,Wilken T,Holzwarth R,Hänsch T W,Udem T 2009Phys.Rev.A80 022503

[41]Coursey J S,Schwab D J,Tsai J J,Dragoset R A 2015Atomic Weights and Isotopic Compositions(version 4.1)[Online]Available:http://physics.nist.gov/Comp[2016,May,27]National Institute of Standards and Technology,Gaithersburg,MD

[42]Yu G H,Liu H,Zhao P Y,Xu B M,Gao D L,Zhu X L,Yang W 2017Acta Phys.Sin.66 113101(in Chinese)[余庚华,刘鸿,赵朋义,徐炳明,高当丽,朱晓玲,杨维 2017物理学报66 113101]

[43]Shabaev V M 1985Theor.Math.Phys.63 588

[44]Shabaev V M 1988Sov.J.Nucl.Phys.47 69

[45]Zhang P P,Zhong Z X,Yan Z C,Shi T Y 2015Chin.Phys.B24 033101

[46]Yan Z C,Drake G W F 2003Phys.Rev.Lett.91 113004

[47]Tupitsyn I I,Kozlov M G,Safronova M S,Shabaev V M,Dzuba V A 2016Phys.Rev.Lett.117 253001