多个子玻色-爱因斯坦凝聚气体膨胀叠加形成的量子涡旋现象研究

董毕远 徐志君

(浙江工业大学应用物理系,杭州 310023)

1 引 言

自1995年首次实现弱相互作用原子系统的玻色-爱因斯坦凝聚(Bose-Einstein condensation,BEC)[1−3]以来,有关BEC的研究发展迅速.1997年,BEC相干性获得了验证[4],接着观察到了一系列新现象,如约瑟夫森效应[5,6]、涡旋[7−10]、超冷费米原子气体等[11,12].其中量子涡旋现象的研究引起了特别关注[13−19],比如涡旋与反涡旋形成的机制研究[20]、由涡旋引起的量子振荡[21]现象的产生以及涡旋与涡旋相互作用[22]等已成为近期研究的热点.本文在Ruben和Paganin[23]基于Gross-Pitaevskii方程,运用数值计算方法研究多个子BEC(many sub-BECs)在自由空间演化叠加形成的量子涡旋的基础上,运用传播子理论,在一定近似条件下,用解析的方法研究了对称分布的三个子BEC在弱磁阱中叠加形成的量子涡旋现象.将我们的研究方法运用到自由空间,所得结论与Ruben和Paganin的数值模拟结果一致,表明本方法的可靠性.在谐振势阱内,得到了一些新的现象,如量子涡旋核随着时间演化产生振荡,其振荡频率就是谐振势的频率,而且形成的涡旋与反涡旋的分布会随时间演化而相互转变.最后对所得到的新现象进行了物理分析和讨论.

2 物理模型

以二维模型为研究对象,也就是典型的碟形BEC系统,即凝聚体横向受到较弱的谐振势作用,而轴向受到很强的囚禁势束缚,从而使凝聚气体轴向分量被冻结在基态,形成典型的碟形BEC系统.实验上将一定形状和强度的激光束打到二维BEC上[24],可将BEC分割为多个子BEC,调节激光束的强度,还可改变各子BEC间的相位关系.然后关闭激光束,让这些子BEC在谐振势阱内膨胀,观察多个子BEC叠加所产生的量子涡旋现象.设谐振势为

其中m为原子质量,ω为径向谐振频率.

相比分割BEC的激光束强度,谐振势是很弱的,因此,可忽略谐振势对各子BEC初始分布的影响.若把分割激光束形成的势能近似为简谐势,则初始各子BEC的分布可近似为高斯分布,即

关闭激光束后,多个子BEC开始在外加二维谐振势阱中膨胀叠加,由于势阱弱,子BEC膨胀时,可忽略原子间的相互作用,因此,此后波函数随时间的演化可近似用传播子来描述.在二维谐振势阱中的传播子为

式中的i是虚数单位,则第j个子BEC随时间演化的波函数为

设初始时刻t′=0,第j个子BEC波函数初相位为ϕj.将(2)和(3)式代入(4)式,并引入参量σ=ω/ω′,直接积分可得第j个子BEC的宏观含时波函数为

得到各子BEC随时间演化的宏观波函数,就能进一步研究相位涡旋形成的物理机制.

3 涡旋形成机制分析

为便于利用数值计算显示涡旋的形成,将(5)式进行无量纲化,做如下变换:

即t用ω−1做单位,|r|用a0做单位,并将ψ用进行归一化.于是带波浪线的变量为无量纲变量,方程(5)可简化为

有了方程(7),就可解析地研究各子BEC膨胀叠加形成涡旋的物理机制.为便于深入分析和计算,考虑对称分布的三个子BEC的叠加情况.即有

取三个子BEC的初始位置为(0,0),(2,0),(1,1.73),即初始为正三角分布,如图1所示.

图1 三个子BEC初始分布情形Fig.1.Three initial distribution of the sub-Bose condensed gas.

不失一般性,设初相位均为零,取σ=20,可将由方程(8)得到的BEC密度和相位随时间的演化用图2显示出来.图中灰度值越小,对应气体密度越大;而相位图中从亮到暗对应相位取值从π变化到−π,在相位图中围绕某一点顺时针或逆时针绕行一周,相位取值从π逐步变化到−π,那么此点便是涡旋核的位置,对应密度图中密度等于零的位置,比如图2(b)中的A点.

图2 BEC密度和相位随时间的演化 从(a)—(f)相应的演化时间为0.25π,0.5π,0.75π,π,1.25π,1.5πFig.2.The time evolution of the BEC density and phase diagram:the evolution time from(a)to(f)is 0.25π,0.5π,0.75π,π,1.25π,1.5π.

图2表明,形成的量子涡旋核呈六边形蜂窝形分布,其涡旋核位置随时间周期性振荡,振荡频率恰好为谐振势阱的频率.当˜t=0.5π(四分之一周期),涡旋核分布在距初始点距离极大值处(图2(b)),之后三个子BEC收缩到与初始分布对称的位置,即位于(0,0),(−2,0),(−1,−1.73)处,完成半个周期振荡(˜t=π,图2(d));后半个周期重复前半个周期的振荡,三个子BEC最终会回到初始(0,0),(2,0),(1,1.73)(图1),完成一个周期振荡.从密度图分析,(图2(c))与(图2(e))时刻,(图2(b))和(图2(f))时刻,涡旋核位置分布情况没有区别,但从相位图看,两者对应的涡旋方向相反(详见图3),因此,前后半个周期,演化情况并不相同.为进一步分析涡旋形成的特点,由方程(8)可以求得体系的粒子流密度

不妨将(7)式中振幅因子与相位因子分开,改写为

其中

这样粒子流密度可以表示为

定义粒子流速度

发现有

即标量场梯度的旋度为零.定义一个环流量

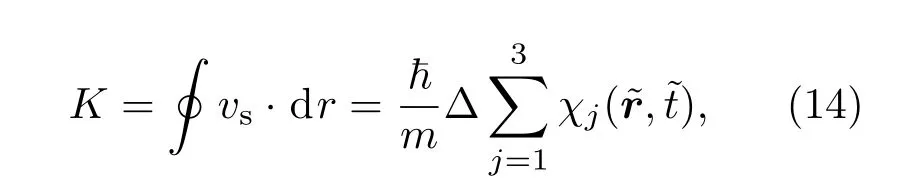
由无旋性质可知K值与路径的选择无关.由波函数的周期性边界条件可知

当l=0时,没有涡旋,l=0有涡旋.即三个子BEC的相图矢量形成闭合三角形时,就会有涡旋产生.将l＞0形成的涡旋记为正涡旋,l＜0形成的涡旋记为反涡旋.由(15)式可以判断涡旋是否形成.

图3 密度与粒子流密度叠加图(a)=0.5π;(b)=1.5πFig.3.Density function and particle flow density diagram:(a)=0.5π;(b)=1.5π.

本文讨论的相位涡旋形成是基于三个不同子BEC(即相当于三个存在一定相位关系的物质波波源)的膨胀叠加,当它们间的相位满足一定条件时便能形成涡旋核.因此,这与通过对BEC旋转等方式产生的涡旋机制不同.对超流系统旋转是否形成涡旋,可通过计算超流体系环流量来判定.对相位涡旋的形成,本文引入粒子流密度,类似地借助定义环流量的概念,利用波函数的周期性边界条件得到判定涡旋存在的(15)式.这与超流涡旋形成判定条件的数学依据是一样的,只不过本文体现在三个子BEC相位叠加为2π的整数倍,而超流则体现在体系环路积分对应的相位角变化量为2π的整数倍.从数学角度来看,两者是等价的.

与(16)式相比,即形成与其对应的反涡旋.因此,当演化时间满足关系时,涡旋核位置相同,而对应的涡旋演变成反涡旋.

4 涡旋核的振荡分析

接下来解释涡旋核分布振荡的现象. 针对三个子BEC初始位置以正三角形分布于(0,0),(2,0),(1,1.73)处,并设三个子BEC初始相位相同,波函数振幅相同.振幅项中因为三个子BEC扩散的时间相同,所以变量应该取相同值;BEC在相对其最大扩散极限的谐振子内扩散时,近似有因此,可以认为(10)式振幅项中的指数项差别可以考虑不计.利用上面推导涡旋形成条件(15)式可以写出涡旋核满足的方程式为

图4 BEC分布及叠加示意图 (a)各子BEC中心位置及演化时空坐标;(b)振幅矢量叠加示意图Fig.4.The diagram of BEC distributed and superimposed:(a)The center position of each sub-BEC and the evolutionary of space-time coordinates;(b)the diagram of superimposed of amplitude vector.

其中m和n均是整数.在确定m,n后可以改写

将(20)和(19)式相比可得如下关系式:

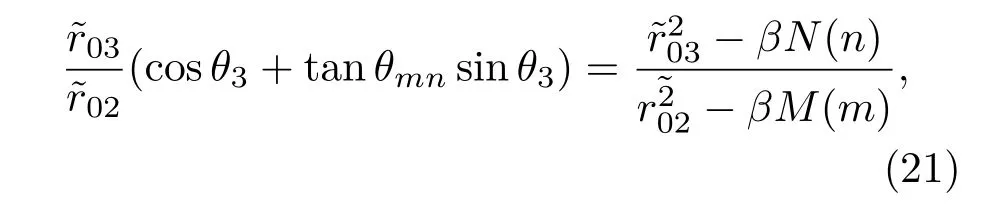
将(22)式代入(20)式,可以得到

在给定如下参数的情形下,即取初始位置为(0,0),(2,0),(0,1.73),θ3=π/3,不考虑初相位,且n=m=0(即l=1情形的涡旋核),可以给出涡旋核随时间演化的分布图像,如图5所示.

因为考虑到图5是所有l=1情形的涡旋核随时间演化的分布图像,故不考虑图中振幅大小的意义,而是考虑核振荡的周期与谐振势的振荡周期之间的关系.结果可以看到涡旋核的振荡,考虑到涡旋旋转的方向,其核振荡的周期与谐振势的振荡周期是相同的.

取相同初始条件,可以给出n=m=−1(即l=−1情形的涡旋核),涡旋核随时间演化的分布图像,如图6所示.

通过对比图5(b)和图6(b)可以发现有一个偏移量,这个偏移量的大小就是六边格子分布的涡旋与邻近反涡旋间的距离.

图5 涡旋核随时间的变化 (a)(x-y-t)视图;(b)(x-y-0)视图;(c)(0-y-t)视图;(d)(x-0-t)视图Fig.5.Diagram of vortex core with time:(a)(x-y-t)view;(b)(x-y-0)view;(c)(0-y-t)view;(d)(x-0-t)view.

图6 涡旋核随时间的变化 (a)(x-y-t)视图;(b)(x-y-0)视图;(c)(0-y-t)视图;(d)(x-0-t)视图Fig.6.Diagram of vortex core with time:(a)(x-y-t)view;(b)(x-y-0)view;(c)(0-y-t)view;(d)(x-0-t)view.

图7 密度与粒子流密度叠加图 (a)—(f)相应的演化时间为0.2π,0.4π,0.6π,0.8π,π,1.2πFig.7.Density function and particle fl ow density diagram:the evolution time from(a)to(f)is:0.2π,0.4π,0.6π,0.8π,π,1.2π.

通过一系列其他时刻的粒子流密度矢量图(如图7所示)来分析涡旋核位置随时间的演化.在图7中跟踪两个涡旋核,标记B点是顺时针涡旋核,C点是逆时针涡旋核.通过观察图7(a)—(d)中B点涡旋核的运动轨迹,可以得到与图5中时间取0到π的轨迹是一致的,振幅大小不同是为了得到(18)式,将振幅项做了近似导致的.从图7(f)可以得到B点的涡旋方向变成逆时针,而C点的涡旋方向变成顺时针,这满足前面推导的涡旋反涡旋转化规律.涡旋核运动轨迹还是沿着原路径直线返回,从而形成一个周期振荡.这与图5中时间取π到2π的轨迹一致,但是方向相反,其中方向相反可以由初始位置的改变得到解释.当时间从π开始取时,三子BEC初始位置变化为原点对称处,即代入(22)式θmn不变,而代入(23)式有故与图5中时间取π到2π的轨迹一致,方向相反.

5 结 论

基于当前实验普遍采用的二维模型,构建多个子BEC在二维空间膨胀叠加的物理模型,在谐振近似下,以高斯分布来构造子BEC初始波函数,然后用传播子方法解析求解出波函数在弱谐振势阱中随时间的演化.本文着重研究了对称分布的三个子BEC膨胀叠加形成涡旋的情况,得到子BEC融合形成的涡旋随时间演化的规律.涡旋核分布随着子BEC在谐振势阱内膨胀而出现振荡,其振荡频率与谐振势的频率相同;同时,还出现涡旋与反涡旋对,在演化的同一时刻,近邻涡旋方向总是相反的,而不同演化时刻,涡旋方向也会出现转化,特别是演化时间满足˜t′=2π−˜t关系时,涡旋核位置相同,而对应的涡旋旋转方向相反.对这一现象,从量子涡旋的基本规律出发进行了解释和探讨.特别是引入粒子流密度,采用类似超流涡旋的思想,计算了环量,分析了涡旋形成的机制.应用本文的研究思路和方法,可方便推广到多于三个子BEC叠加形成涡旋机制的研究,也可讨论各子BEC有不同初始相位差时对涡旋的影响等,均可得到一些有意义的结果.这一模型在实验上也比较容易实现.因此,本文的研究对实验工作也有启示意义.

[1]Davis K B,Mewes M,Anderson M R,Druten N J,Durfee D S 1995Phys.Rev.Lett.75 3969

[2]Anderson M H,Ensher J R,Matthews M R,Wieman C E,Cornell E A 1995Science269 198

[3]Bradley C C,Sacket C A,Tollent J J,Hulet R G 1995Phys.Rev.Lett.75 1687

[4]Andrews M R,Townsend C G,Miesner H J,Durfee D S,Kurn D M,Ketterle W 1997Science275 637

[5]Burnett K 1998Science282 1657

[6]Anderson B P,Kascvich M A 1998Science282 1686

[7]Matthews M R,Anderson B P,Haljan P C,Hall D S,Wieman C E 1999Phys.Rev.Lett.83 2498

[8]Xu Z J,Shi J Q,Lin G C 2007Acta Phys.Sin.56 666(in Chinese)[徐志君,施建青,林国成 2007物理学报 56 666]

[9]Bloch I 2005Nature434 23

[10]Lundh E,Pethick C J,Smith H 1998Phys.Rev.A58 4816

[11]Fölling S,Gerbier F,Widera A,Mandel O,Gericke T,Bloch I 2005Nature434 481

[12]Cheng L C,Meng Z M,Wang P J 2017Acta Phys.Sin.66 083701(in Chinese)[陈良超,孟增明,王鹏军 2017物理学报66 083701]

[13]Madison K W,Chevy F,Wohlleben W 2000Phys.Rev.Lett.84 806

[14]Leanhardt A E,Shin Y,Kielpinski D,Pritchard D E,Ketterle W 2003Phys.Rev.Lett.90 140403

[15]Scherer D R,Weiler C N,Neely T W,Anderson B P 2007Phys.Rev.Lett.98 110402

[16]Kläui M,Vaz C A F,Lopezdiaz L,Bland J A C 2003J.Phys.:Condens.Matter15 R985

[17]Talos D M,Follett P L,Folkerth R D,Fishman R E,Trachtenberg F L 2007New J.Phys.9 95

[18]Glover G M C,Fitzpatrick J J 2007Chem.Eng.J.127 11

[19]Li Y Q,Li X G,Liu Z Y,Luo P Y,Zhang P M 2007Acta Phys.Sin.56 6178(in Chinese)[李永青,李希国,刘紫玉,罗培燕,张鹏鸣2007物理学报56 6178]

[20]Sakaguchi H,Li B,Malomed BA 2014Phys.Rev.E89 032920

[21]Villaseñor B,Zamora-Zamora R,Bernal D,Romero-Rochín V 2013Phys.Rev.A89 1964

[22]Wells T,Lode A U J,Bagnato V S,Tsatsos M C 2015J.Low Temp.Phys.80 1

[23]Ruben G,Paganin D M 2007Phys.Rev.E75 066613

[24]Scherer D R,Weiler C N,Neely T W,Anderson B P 2007Phys.Rev.Lett.98 110402