抗磁悬浮振动能量采集器动力学响应的仿真分析∗

秦立振 张振宇 张坤 丁建桥 段智勇 苏宇锋

1)(郑州大学机械工程学院,郑州 450001)

2)(郑州大学物理工程学院,郑州 450001)

1 引 言

近年来,植入式医疗设备、无线传感器网络等得到了广泛的应用,但是这些设备的电能供应仍然依赖于传统电池[1].传统电池具有使用方便、成本低廉的优点,但同时也具有持久性差、储能有限的缺点.在一些无法更换电池或更换电池的成本比较高的场所,传统电池显现了其固有的局限性.因此,开发一种在用电设备有效寿命结束之前无需维护的永久电池成为各国研究者关注的课题之一.自然环境中存在着各种各样的能量,利用环境中的能量为电子元器件供电是取代传统电池的有效途径[2].

能量采集技术的主要原理是利用光伏效应、压电效应、热电效应、电磁感应等,将周围环境中的能量转化为电能,然后利用储能元件进行电能存储,最后通过相应的电源管理电路,将存储的电能提供给外部负载,进而为用电设备供电.能量采集不仅涉及能量转化利用的问题,同时也涉及优质能量来源的问题.相对于光、风、热等,振动能量具有分布范围广、能量密度高、易于采集的特点,因此振动能量采集是目前研究较多的一种能量采集方案[3].

振动能量的采集存在不同的途径,基于不同的原理、方法和材料.1939年,Braunbek和Schweben[4]首次利用非均匀电磁场实现了微小片状石墨的稳定悬浮,此后,抗磁悬浮得到了越来越多的关注和研究.意大利都灵理工大学的de Pasquale等[5]利用钕铁硼(NdFeB)强磁铁和高定向热解石墨(HOPG)抗磁材料,在常温下获得了1—2 mm的悬浮高度.抗磁悬浮由于能够在常温下实现无摩擦稳定悬浮,所以得到了越来越多的应用.目前,抗磁悬浮原理已被应用到生物医学[6,7]、传感器[8]、微执行器[9]、微型电机[10]等领域.基于这一原理,我们课题组开展了微型抗磁悬浮振动能量采集器的研究[11,12],本文研究了该能量采集器的振动响应特性.

2 结构模型和工作原理

抗磁悬浮振动能量采集器的主要部件包括:提升永磁体、悬浮永磁体、上热解石墨板、下热解石墨板以及布置在上下热解石墨板内表面的平面螺旋线圈,其结构如图1所示.

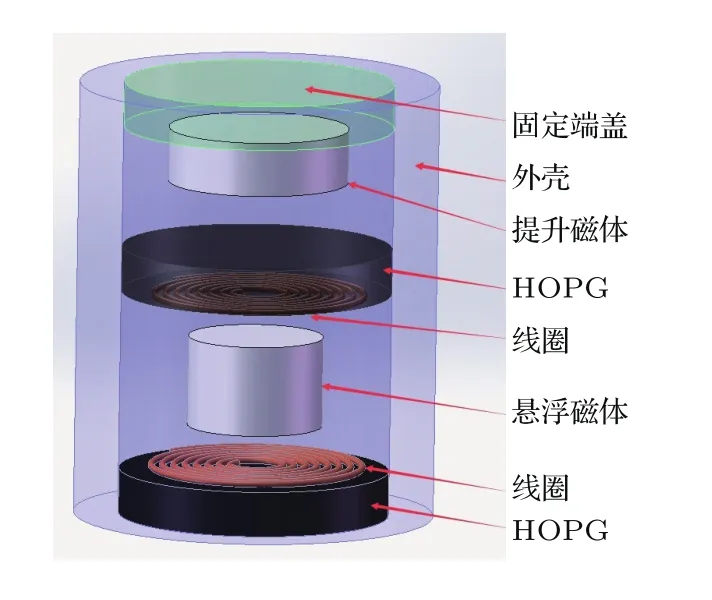
图1 抗磁悬浮振动能量采集器的结构模型Fig.1.The structure model of diamagnetic levitation vibration energy harvester.

由于提升永磁体和悬浮永磁体都是圆柱形且磁化方向都沿轴向,所以提升永磁体的磁场会在水平方向上形成一个磁势阱.根据能量最小原理,悬浮永磁体在水平方向上能够稳定悬浮且平衡点位于两永磁体的公共轴线上.高定向热解石墨是常温下抗磁性最强的材料,表现为对外界磁场的排斥作用.在竖直方向上,悬浮永磁体同时受到重力、提升磁体吸引力的竖直分量、热解石墨板的抗磁力.在满足特定的尺寸参数条件下,竖直方向上也能够稳定悬浮,所以悬浮永磁体处于一个三维势阱之中能够稳定悬浮.当系统受到外界干扰时,悬浮磁体可以在平衡位置附近振动,从而将外界振动转化为悬浮磁体的振动.根据法拉第电磁感应定律,悬浮磁体振动的机械能转化为线圈内部的电能[11].

3 结构参数和受力分析

抗磁悬浮振动能量采集器的结构参数和材料参数直接决定了悬浮磁体的受力状态,进而影响能量采集器的振动响应特性和能量转化效率,其结构材料参数如表1所列.

当悬浮永磁体发生振动时,其不但会受到重力、抗磁力、提升永磁体的吸引力,还会受到空气和感应线圈的阻尼力.文献[13—16]给出了永磁体之间以及永磁体和热解石墨板之间受力的理论关系式,但这些关系式并不是显式且过于复杂,不便于进行动力学响应分析,因此采用COMSOLTM仿真并结合数值拟合的方法获得磁力和抗磁力的近似表达式.本研究中悬浮永磁体受力的仿真计算模型如图2(a)和图2(b)所示.

表1 抗磁悬浮能量采集器结构参数Table 1.The structure parameters of diamagnetic levitation energy harvester.

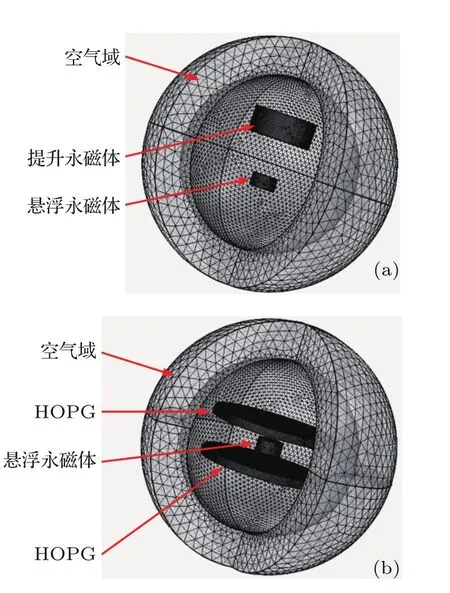
图2 磁力和抗磁力计算模型Fig.2.The calculational model of magnetic force and diamagnetic force.

永磁体和热解石墨板周围的空气域分为两层,外层设为无限域模拟磁体的弥散场,且网格划分较粗,内层是有限域且网格划分较细,以节省仿真时间并兼顾仿真精度,磁体的和热解石墨板的网格最细以提高仿真精度,单元类型采用自由剖分四面体网格,最大生长率为1.6,曲率因子为0.6,狭窄区域解析度为0.5.当网格的精度不断增加时,仿真结果越趋近于定值且变化越来越慢.为了兼顾时间和精度,分析中网格最大单元尺寸选定如下:无限空气域5 mm,有限空气域2 mm,磁体和热解石墨板0.8 mm.图2(a)和图2(b)中模型单元数分别为661370和920624.

对仿真结果进行数据拟合求得磁力F1的解析式为

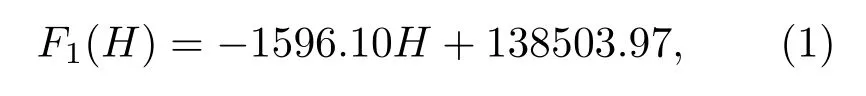
式中,H为提升永磁体和悬浮永磁体之间的距离,单位为mm;F1单位为µN.

抗磁力F2的解析式为

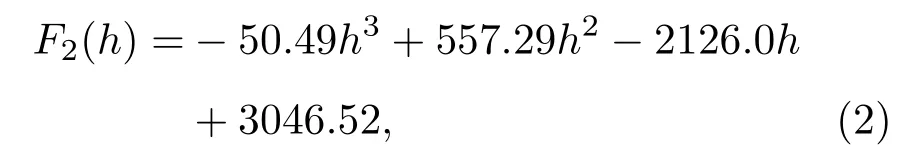
式中,h为悬浮永磁体和热解石墨板之间的距离,单位为mm;F2单位为µN.

感应线圈工作时悬浮永磁体受到的电磁阻力Fεγ

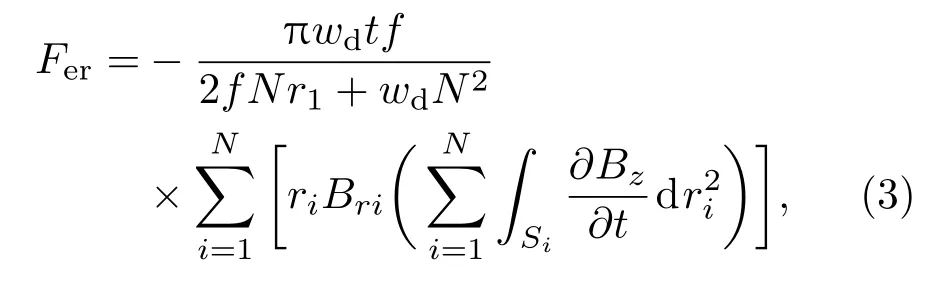
式中,Bri为第i匝线圈所在位置磁感应强度在径向上的分量,Bz为磁感应强度在轴向上的分量,ri为第i匝线圈的半径.

对(3)式利用响应面法求得悬浮磁体周围磁场在轴向和径向上的分布,最终求得其电磁阻尼力的表达式为

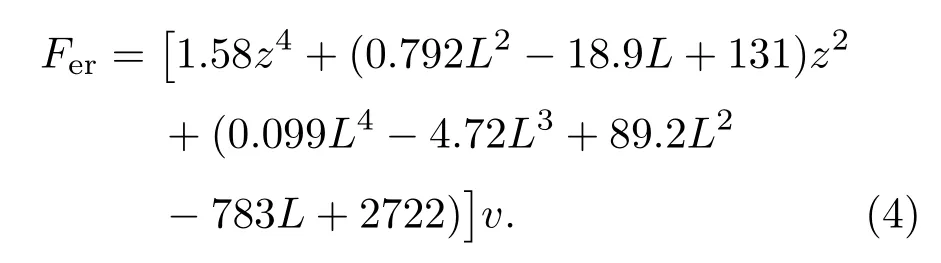
悬浮磁体的运动属于低幅低频运动,因此其受到的空气阻力可以用(5)式近似计算:

式中,S为迎风面积,k为阻力系数.

以两热解石墨板对称面的中心为零点,向上设为正方向,统一坐标系后,在竖直方向上振动的动力学方程如(6)式所示:

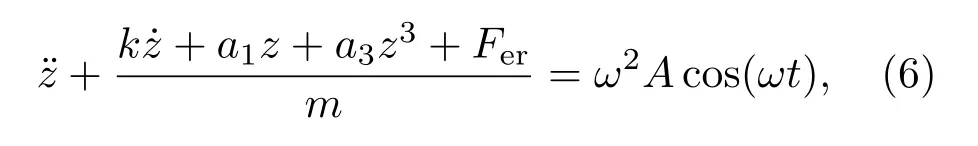
其中,a1,a3由F1和F2决定,ω=2πf为外界激励频率,A为激励振幅.

4 运动特性

悬浮磁体所受磁力、抗磁力和重力的合力随热解石墨板间距L的变化曲线如图3所示.通过分析其受力曲线可以发现,其受力曲线的非线性程度随着两热解石墨板间距的增大而增强.

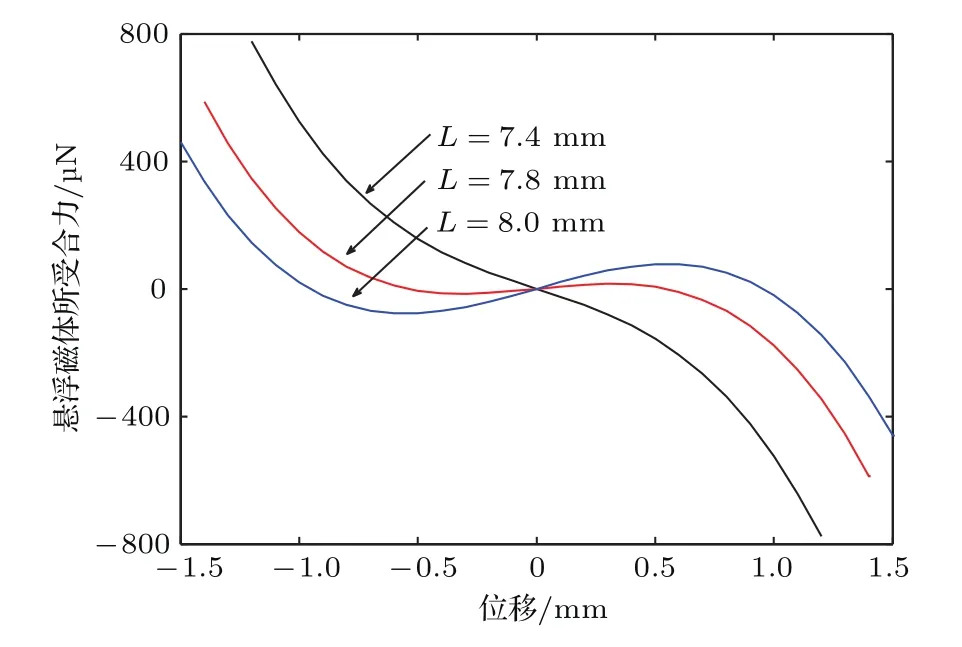
图3 悬浮磁体所受合力Fig.3.The resultant curves of the fl oating magnet.

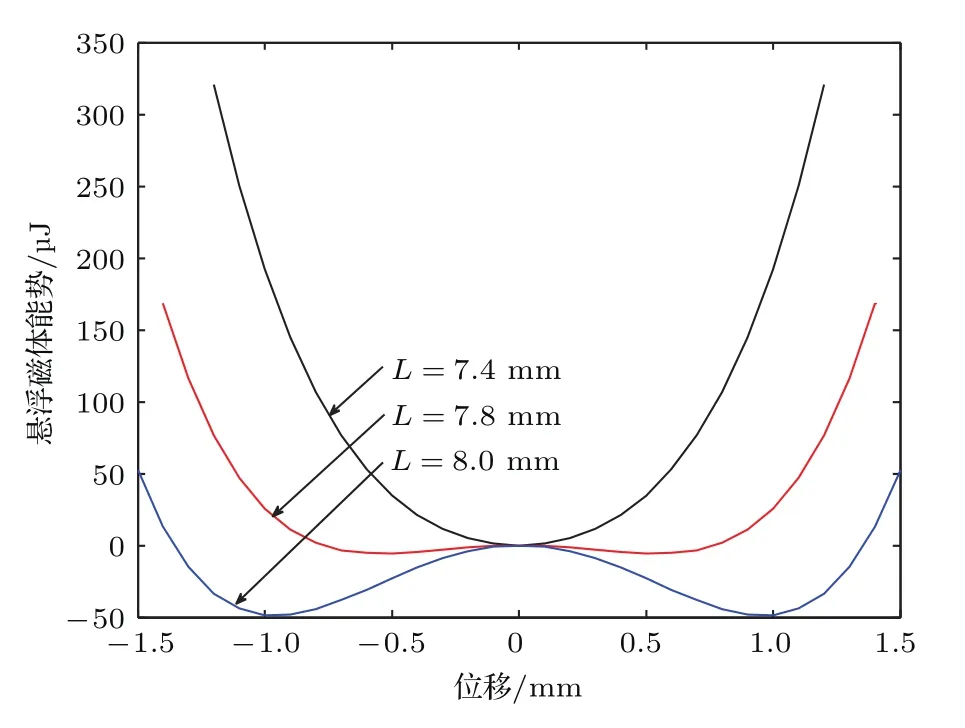
图4 悬浮永磁体势能曲线Fig.4.The potential energy curve of the fl oating magnet.

图4是悬浮永磁势能随热解石墨板间距变化的曲线.发现当两热解石墨板间距L＞7.7 mm时,势能曲线会出现两个势阱,而在L＜7.7 mm时,只存在一个势阱.由能量最小原理可知,悬浮永磁体的稳定平衡位置就是磁势阱的位置.

图5是当热解石墨板间距L分别为7 mm和8 mm时,悬浮磁体的静止平衡现象.由实验现象可知热解石墨板间距的变化会导致悬浮永磁体稳态类型发生改变,即单稳态类型和双稳态类型,分别如图5(a)和图5(b)所示.

图5 悬浮磁体的单稳态(a)和双稳态(b)现象Fig.5. The monostable(a)and bistable(b)phenomenon of the fl oating magnet.

4.1 单稳态类型时的动力学响应

文献[17]给出了当能量采集器处于非工作的单稳态状态时悬浮磁体振动的幅频关系方程:

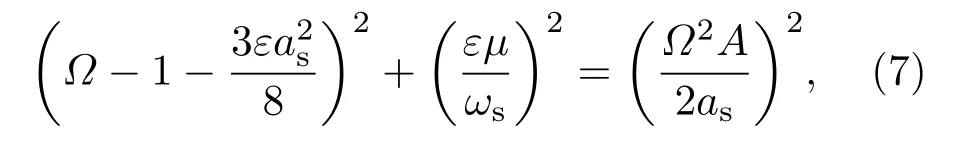
当能量采集器处于单稳态类型时,悬浮磁体只有一个平衡位置.当受到外界激励时,悬浮磁体在平衡位置附近往复运动.选择热解石墨板间距L=7,7.4 mm研究单稳态类型时悬浮磁体的振动特性.图6是外界激励幅值为1 mm、感应线圈处于开路状态(非工作状态)时悬浮磁体的幅频响应曲线.可以发现悬浮磁体的幅频响应曲线向右偏斜,呈现“硬弹簧”特质,并且随着热解石墨板间距的增加,曲线向右偏斜程度增强.当热解石墨板间距L为7 mm和7.4 mm时,悬浮磁体振动的基频分别为2.37 Hz和1.5 Hz.增大热解石墨板间距,悬浮磁体的振动响应频带变宽并出现多解和跳跃现象.

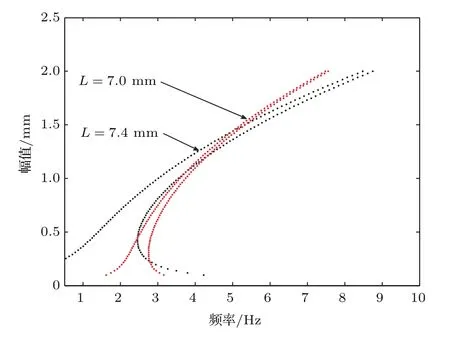
图6 振幅随激励频率变化的曲线Fig.6.The curve of amplitude changes with excited frequency.

图7是热解石墨板间距分别为7 mm和7.4 mm,感应线圈工作时,悬浮磁体的相对位移随外界激振幅值和频率的变化关系.当外界激励相同,增大热解石墨板间距能获得更大的相对运动位移.

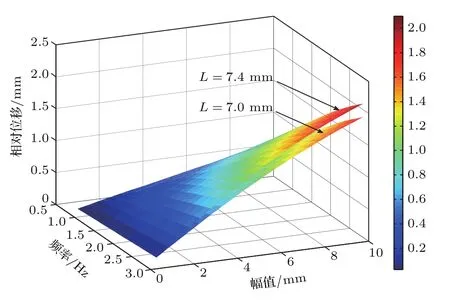
图7 单稳态类型时位移峰值随外界激励的变化Fig.7.Displacement peaks change with the external excitation in monostable type.

4.2 双稳态类型时的动力学响应

当采集器处于双稳态类型时,此时的动力学方程的解Z(t)可以看作一势子在势场U(z)中的运动,当没有外界激励时,U(z)=a1z2/2+a3z4/4,是一种双稳势场结构,由dU(z)/dz=0很容易得出系统平衡点Zm1,Zm2,Zb位置,分别如(8)和(9)式所示:

当受到外界周期激励时,系统的势函数受到周期调制,由U(z)变为V(z),如(10)式所示:

由(10)式可以看出,势函数的势阱被周期性地抬高或加深.此时,系统存在一临界幅值Ac,使得方程保持双稳结构.当外界周期激励的幅值A＜Ac时,势阱周期性的抬高或加深不足以使势垒消失,势子无法越过势垒进入另一势阱,只能在单阱中做小幅振荡;当外界周期激励幅值A＞Ac时,由于势垒可能随着时间的变化而消失,势子能够越过势垒在两势阱间进行大位移周期性跳跃.临界幅值Ac表示系统势函数V(z)在Acos(2πft)为最大值或最小值时恰好从双稳态结构变成单稳结构.

图8 双稳态类型时悬浮永磁体共振分岔图Fig.8.The resonant bifurcation diagram of fl oating magnets in bistable type.

两热解石墨板的间距不仅影响采集器的稳态类型同时也影响悬浮磁体的平衡位置.当L=7.8 mm时,悬浮永磁体在x=±0.51 mm处稳定悬浮.动力学方程的初始条件可以任选其一,此处选择x=0.51 mm.感应线圈开路时,悬浮磁体振动幅值随外界激励的分岔图,如图8所示.由图8可以看出,感应线圈开路时,当外界激励频率为1 Hz,激励振幅从0.2—4 mm的变化过程中,系统出现了2倍周期—4倍周期—混沌—双倍周期-单倍周期变化的现象.

表2是不同外界激振参数下,当热解石墨板间距L=7.8 mm时悬浮磁体的振动相图及其对应的Poincare映射图.当非线性系统和线性系统进行耦合时,两系统之间的强弱关系会直接影响到系统的振动响应特性:当其中一个系统弱到整个系统可以看做两个独立的系统,或者其中一个系统强到占统治地位时,整个系统都将处于周期运动状态;只有当两系统的强弱不相上下时,两系统相互影响强烈,运动才变得十分复杂,从而才可能形成混沌[18].

图9是两热解石墨板间距为7.8 mm、感应线圈处于工作状态、外界激励频率为1 Hz、激励振幅从0.5 mm增大到8.5 mm的过程中(每次增加1 mm),悬浮磁体稳态振动的运动相图.从图9可以看出随着激振幅值A的增加,倍周期现象和混沌现象消失,悬浮磁体进行周期振动.

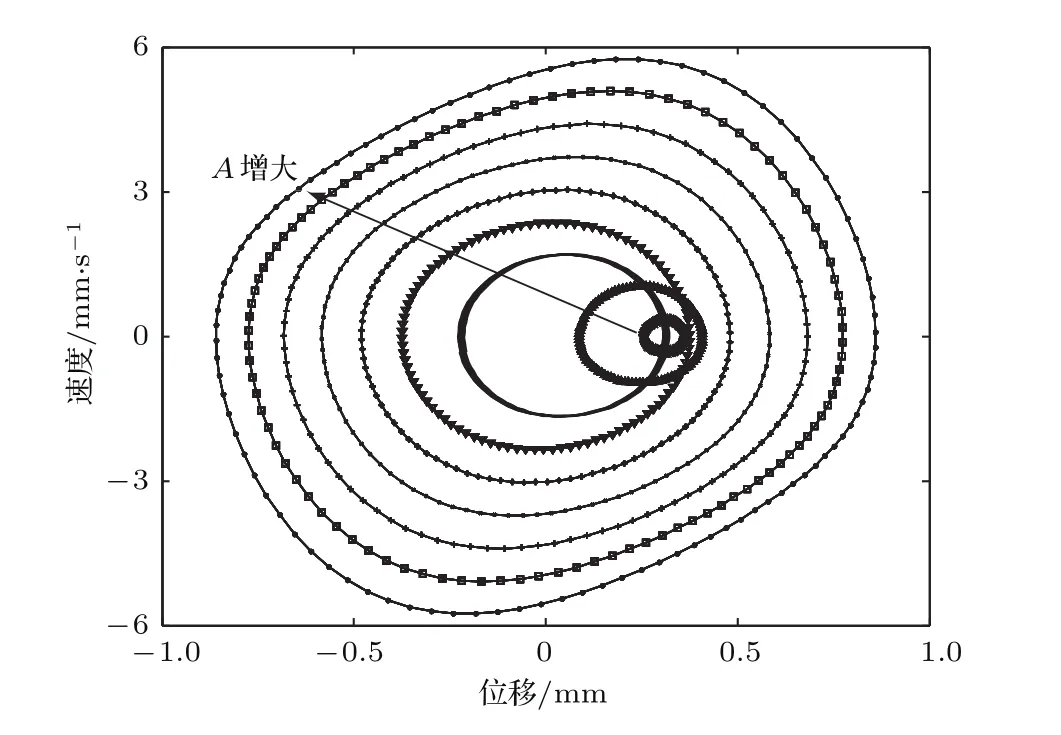
图9 外界激励频率为1 Hz时双稳态类型的运动相图Fig.9.The vibration phase diagram when the excitation is 1 Hz in bistable type.

图10是外界激励频率在0—3.2 Hz,激励振幅在0—10 mm之间变化、系统处于双稳态类型时,悬浮磁体稳态振动的峰值.当激励振幅较小时,悬浮磁体仅能在鞍点一侧振动;当激励振幅足够大时,悬浮磁体跨过鞍点做阱间周期振动.

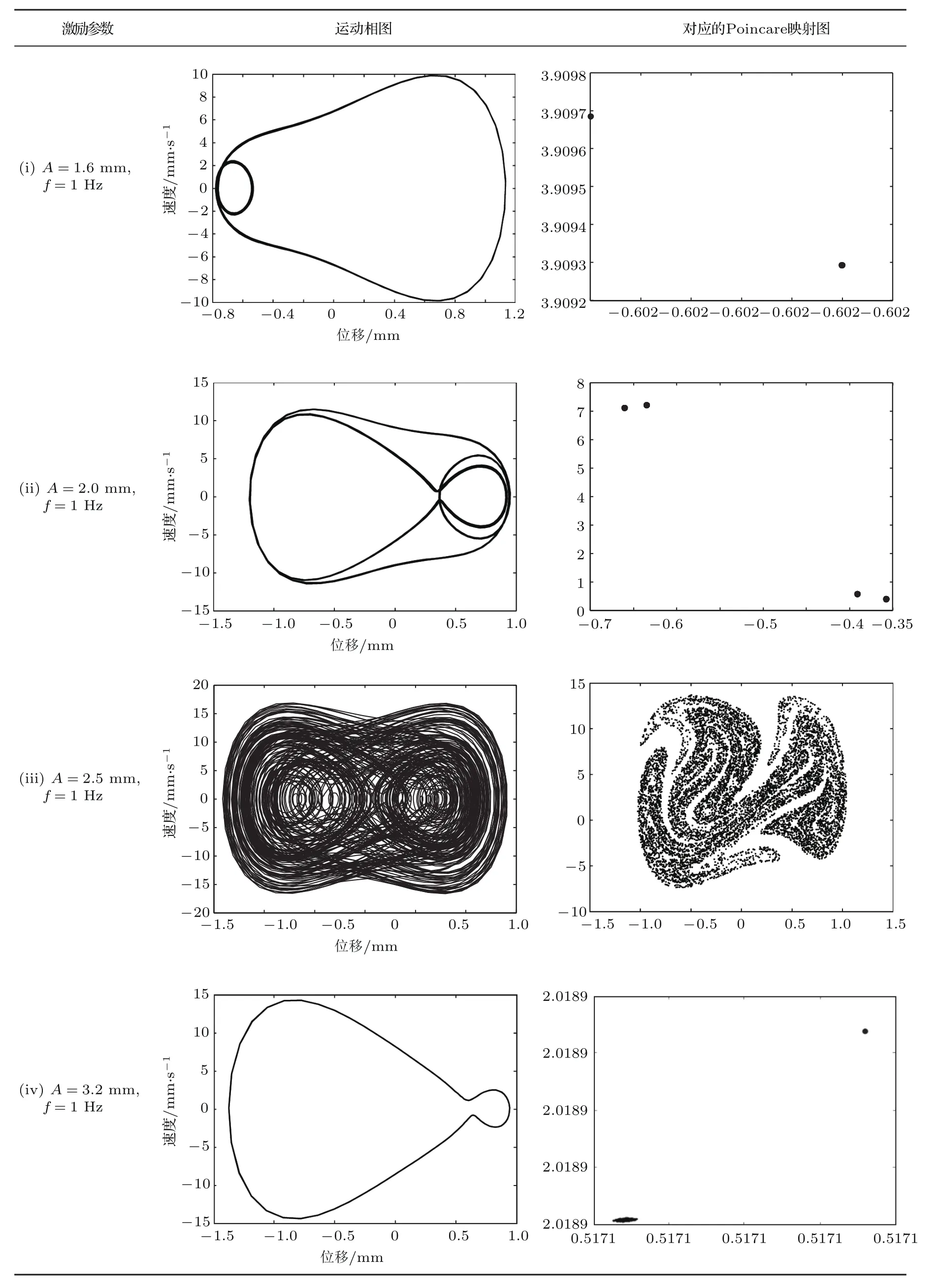
表2 双稳态类型时悬浮磁体的运动相图和对应的Poincare映射图Table 2.The vibration phase diagram and the Poincare mapping diagram of the fl oating magnetic in bistable type.

图10 双稳态类型时位移随外界激励的变化Fig.10.The displacement changes with the external excitation in bistable type.

5 总 结

抗磁悬浮振动能量采集器中悬浮永磁体的运动特性直接决定着其输出特性,悬浮磁体受力的非线性使得能量采集器的动力学响应和能量输出特性较为复杂.本文利用COMSOLTM建立仿真模型,仿真获得悬浮磁体所受的磁力和抗磁力,并进行数据拟合得到磁力和抗磁力的解析表达式.然后,建立了悬浮永磁体的动态响应方程以研究其动态响应特性.在感应线圈开路(非工作状态)时,单稳态类型的幅频响应曲线呈现向右偏斜的现象,并随着热解石墨板间距和非线性扰动的增大而增强.同时发现在相同激励下,石墨板间距越小,采集器的响应幅值越大.当感应线圈开路且采集器处于双稳态类型时,通过分析悬浮磁体的振动相图及其对应的Poincare映射图发现采集器出现了倍周期、4倍周期和混沌等非线性系统特有的现象.当感应线圈处于工作状态且采集器处于双稳态类型时由于受到电磁阻尼力的影响,倍周期和混沌现象消失,悬浮磁体的振动频率和外界激励频率保持一致.该研究是对微型抗磁悬浮振动能量采集器动态特性的深入探索,对该能量采集器的结构设计具有重要的指导意义,加快了该能量采集器的实用化进程.基于本文的研究,可以对能量采集器进行优化,以提高其响应特性和输出性能.此外,本文也是对能量采集器中非线性振动特性研究的补充和丰富,对理解和利用非线性振动具有重要的意义.下一步的工作是研究分析该能量采集器的输出特性,开展动态研究实验,并对实验结果进行对比分析,推动该能量采集器向实用化迈进.

[1]Ma X C,Ye R F,Zhang T L,Zhang X Q 2016Acta Phys.Sin.65 177701(in Chinese)[马星晨,叶瑞丰,张添乐,张晓青2016物理学报65 177701]

[2]Liu L,Yuan F G 2013J.Sound.Vib.332 455

[3]Dai X Z,Wen Y M,Li P,Yang J,Jiang X F 2010Acta Phys.Sin.59 2137(in Chinese)[代显智,文玉梅,李平,杨进,江小芳2010物理学报59 2137]

[4]Braunbek W 1939Z.Phys.112 764

[5]de Pasquale G,Siyanbalapitiya C,Somà A,Wang J 2009International Conference on Electromagnetics in Advanced ApplicationsTorino,Italy,September 14–18,2009 p465

[6]Cao J P,Yin D C,Qian A R,Tian Z C,Xu H Y,Huang Y P,Shang P 2011Chin.J.Space Sci.31 63(in Chinese)[曹建平,尹大川,骞爱荣,田宗成,续惠云,黄勇平,商澎2011空间科学学报31 63]

[7]Sun Y L,Chen Z H,Chen X H,Yin C,Li D J,Ma X L,Zhao F,Zhang G,Shang P,Qian A R 2015IEEE Trans.Bio-Med.Eng.62 900

[8]Billot M,Piat E,Abadie J,Stemp fl é P 2016Sensor.Actuat.A:Phys.238 266

[9]Hiber W,Jakoby B 2013IEEE Sens.J.13 2786

[10]Liu W,Chen W Y,Zhang W P,Huang X G 2008Electron.Lett.44 681

[11]Su Y F,Zhang K,Ye Z T,Zhang K P 2016Instrum.Tech.Sensor10 28(in Chinese)[苏宇锋,张坤,叶志通,张鲲鹏2016仪表技术与传感器10 28]

[12]Ye Z T,Duan Z Y,Takahata K,Su Y F 2015Appl.Phys.A118 91

[13]Qin L Z,Su Y F,Liu W F 2016J.Electron.Meas.Instrum.30 1438(in Chinese)[秦立振,苏宇锋,刘武发2016电子测量与仪器学报30 1438]

[14]Ravaud R,Lemarquand G,Babic S,Lemarquand V,Akyel C 2010IEEE Trans.Magn.46 3585

[15]Su Y F,Ye Z T,Xiao Z M,Takahata K 2015IEEE 10th International Conference on NEMSXi’an China,July 7–11,2015 p116

[16]Liu K,Zhang W P,Liu W,Chen W Y,Li K,Cui F,Li S P 2010Microsyst.Technol.16 431

[17]Xu W 2001Numerical Analysis Methods for Stochastic Dynamical System(Beijing:Science Press)p179(in Chinese)[徐伟 2001非线性随机动力学的若干数值方法和应用(北京:科学出版社)第179页]

[18]Lai Z H 2014Ph.D.Dissertation(Tianjin:Tianjin University)(in Chinese)[赖志慧 2014博士论文 (天津:天津大学)]