非一致通信时滞动力学网络上的接连滞后同步∗

张迪 张银星 邱小芬 祝光湖 李科赞

(桂林电子科技大学数学与计算科学学院,广西密码学与信息安全重点实验室,桂林 541004)

1 引 言

自20世纪80年代,随着以互联网为代表的信息工程技术的迅猛发展,人类已经进入了一个网络时代.我们的身边围绕着各种各样的网络,例如神经网络、社交网络、交通网络、生物网络等.人类社会的日益网络化就要求我们要对这些复杂的网络有更深入的认识.近年来,复杂网络研究取得了一系列重要的研究成果[1,2].

在复杂网络领域,同步现象一直是学者们关注的重点问题.在现实生活中,同步现象普遍存在,例如观众的掌声响亮如雷鸣,过往的行人太多会导致大桥坍塌,各种网络同步的例子数不胜数.当然,有些同步是有利的,有些则是有害的.正因为同步现象的普遍存在,并且具有很大的应用价值,所以近几十年以来,同步被广泛且深入地研究并取得了大量有价值的研究成果[3−7],这些同步包括完全同步[8,9]、部分同步[10]、相位同步[11]、滞后同步[12]、投影同步[13]、广义同步[14]、混沌同步[15]等.

时滞是现实动力系统中普遍存在的一种现象.时滞通常是由于通信距离、信道噪声等因素引起的.近年来,具有时滞的同步现象已经引起了国内外众多学者的广泛关注,并应用在物理学、医学、生物学等多个领域.研究表明,滞后同步的现象不仅会发生在一个网络系统中,而且完全有可能发生在两个网络系统之间.例如文献[16]研究了单个复杂网络里的滞后同步,文献[17—19]研究了两个耦合动力学网络上的广义滞后同步.在这些研究中,主要考虑如何在两个耦合的网络(其中一个为驱动网络,另一个为响应网络)系统之间实现滞后同步.

接连滞后同步是Li等[20]提出的一种复杂动力系统上的新型滞后同步模式,接连滞后同步指的是依据网络节点编号,第i+1个节点与第i个节点接连实现滞后同步,即当t→+∞时,xi(t−τ)→xi+1(t),其中xi表示第i个节点的状态变量,τ为同步时滞.在现实生活中的网络节点之间通常是存在通信时滞的,因此考虑含通信的时滞网络上的同步问题更具现实意义.在文献[20]中没有考虑节点之间的通信时滞,在文献[21]中只考虑带有一致通信时滞的复杂动力学网络上的接连滞后同步.由于网络的复杂性节点与节点往往具有差异性,它们之间的通信时滞也往往会随着节点的不同而不一样.例如,在国庆阅兵时,由一架架飞机组成的飞机网络,为了避免碰撞和保持队形(可视为接连滞后同步),飞机的驾驶员之间要时刻保持联络,但是由于通信距离和驾驶员个体差异等方面的影响,飞机与飞机之间的通信一定会存在时滞现象,而且不同驾驶员之间的通信时滞肯定会有所不同.因此,研究含有不同通信时滞(即非一致通信时滞)的动力学网络上的同步问题将更加具有现实意义.

多智能体系统的一致性是网络同步的一种情形,类似文献[20],本文的工作也可用于多智能体系统一致性的研究.近年来,多智能体系统的一致性受到了广泛关注和深入研究,如文献[22]考虑具有非线性动力学和有向拓扑的多智能体系统的一个二阶一致性问题,其中每个节点都受位置和速度一致性项的影响,且具有时变渐近速度;文献[23]研究了在多拉格朗日系统中没有通信的条件下参数不确定性下的不使用邻居速度信息有向图的分布式协调问题;文献[24]提出多智能体系统的滞后一致性概念,研究了有向网络环境下一阶领导-跟随多智能体系统的滞后一致性问题.

正是考虑到现实生活中处处存在时滞,并且不同节点之间的通信时滞往往是不同的,所以本文构建了含有非一致通信时滞的动力学网络模型,并重点分析了该网络的接连滞后同步的稳定性,得到了同步稳定的充分条件,使得本文的研究更加符合现实的要求;其次,分别设计了线性反馈控制和自适应反馈控制,利用Lyapunov函数方法分析了该网络模型的接连滞后同步的稳定性,获得了同步稳定的充分条件;最后,通过数值模拟验证了理论结果的正确性.

2 预备知识

为了后续理论分析的需要,首先介绍本文将要用到的一些预备知识.

假设网络有n个节点,节点与节点之间存在通信时滞,且不同的节点对应的时滞不一样(即非一致通信时滞),则受控下的复杂动力学网络可描述如下:

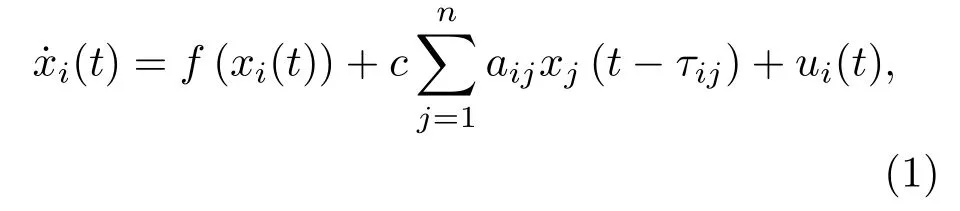
其中i=1,2,...,n,xi(t)=(xi1,xi2,···,xim)T∈Rm表示节点i的状态变量;τij＞0是节点i与j之间的通信时滞(也称传输时滞);常数c＞0是耦合强度;ui(t)代表第i个节点的反馈控制.假设耦合矩阵是不可约矩阵,

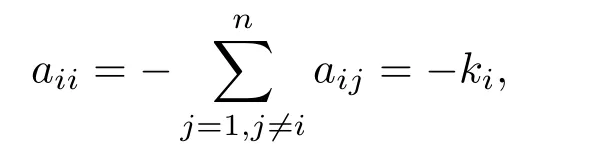
ki是第i个节点的度,当第i个节点与第j个节点有连接时aij=aji=1,当第i个节点与第j个节点没有连接时aij=aji=0,(i̸=j,i,j=1,2,...n).记Γ=(τij)n×n为系统(1)的通信时滞矩阵.

假设1Γ为对称的,τij=τji且τij=τi+1,j+1(i,j=1,2,···,n−1).

记C([−(n−2)τ−max{τij},0],R)为全体从[−(n−2)τ−max{τij},0]到R上连续函数构成的集合.

定义1[20]如果对于任意的初始条件xi(t)=φi(t)∈C([−(n−2)τ−max{τij},0],R)和所有的i∈{1,2,···n−1},都有

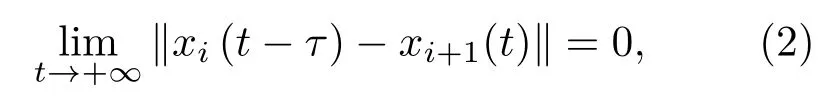
则动力学网络(1)实现了接连滞后同步(successive lag synchronization,SLS),即接连滞后同步是全局稳定的,其中同步时滞τ＞0.

定 义2[25]QUAD(∆,P,ω) 函 数 类:设是 对 角 矩 阵,P=是 正 定 对 角 矩 阵, 函 数若存在ω＞0,以及所有有

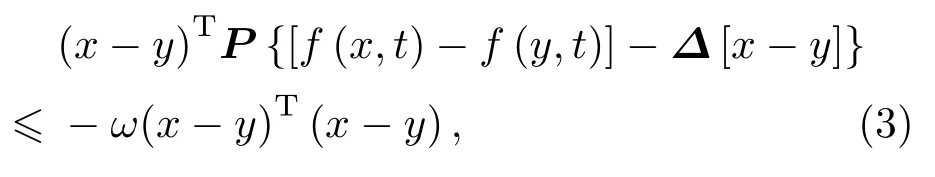
引理1[26]设矩阵M= (mij)p×q,则有不等式

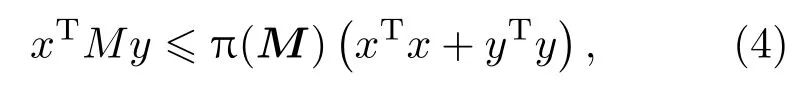
引理2(Barbalat引理)[27]若g(t):R→R+在[0,+∞)为一致连续函数,且极限

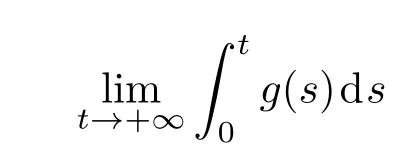
引理3[20]若g(t):在[0,+∞)为一致连续函数,且积分

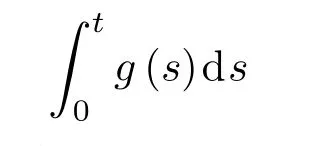
在[0,+∞)上有界,则

引理4[28]对有合适维数的矩阵A,B,C它们之间的Kronecker积⊗满足

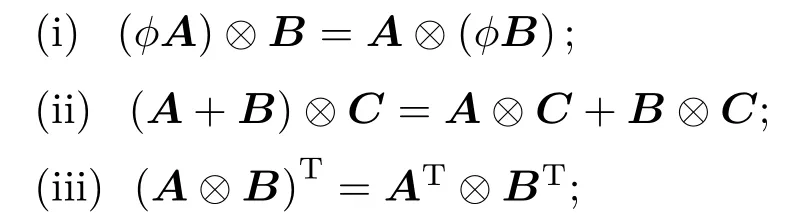
其中ϕ是任意常数.

3 SLS的控制策略及稳定性分析

本节将分别设计线性反馈控制和自适应反馈控制两种方法来达到接连滞后同步,利用Lyapunov函数法和Barbalat引理分析接连滞后同步的稳定性.

3.1 线性反馈控制

为了消除后面误差系统中的抑制项实现接连滞后同步,设计以下的预备函数:

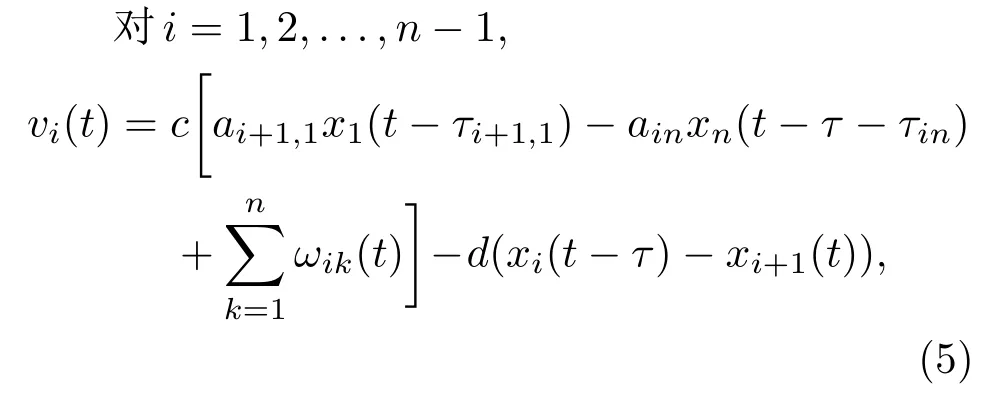
其中d＞0为控制强度,

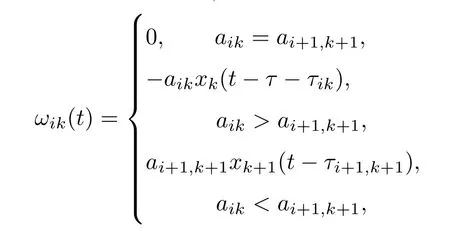
且

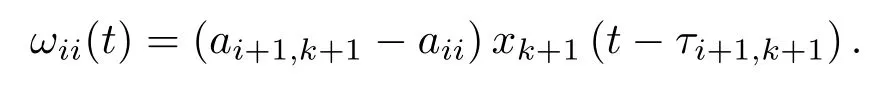
进一步,设计线性反馈控制如下:

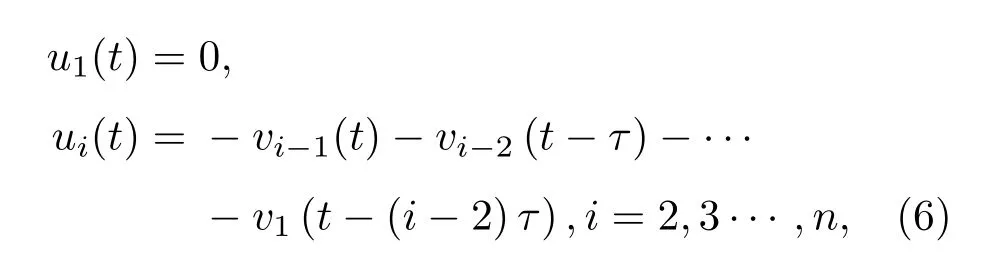
于是得到

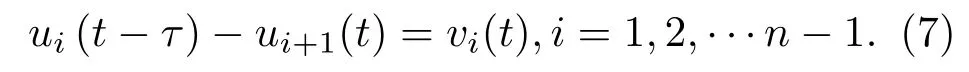
定义同步误差ei(t)=xi(t−τ)−xi+1(t),i=1,2,...,n−1.从而系统(1)的误差系统可描述为

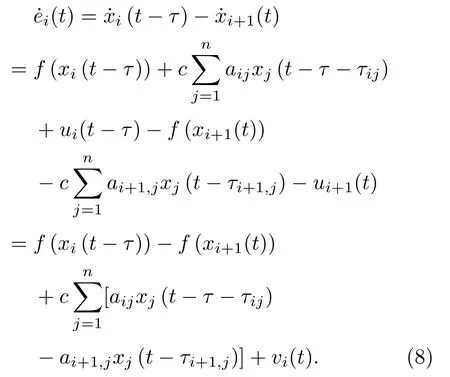
由假设1知τij=τi+1,j+1,结合(8)从而有误差系统

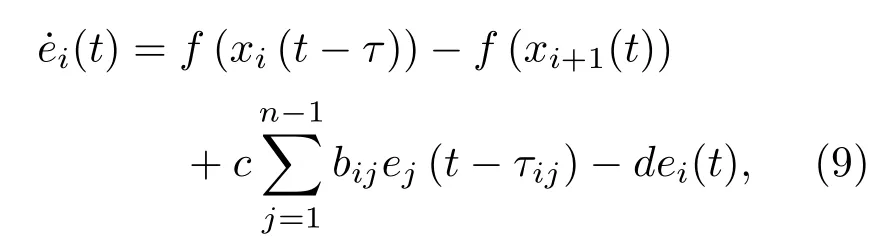
其中

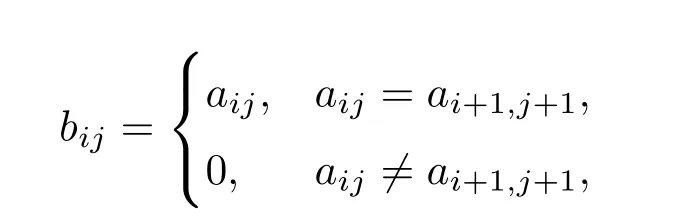
且

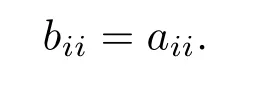
定理1设为对角矩阵,为正定对角矩阵,若且存在d＞0,使得

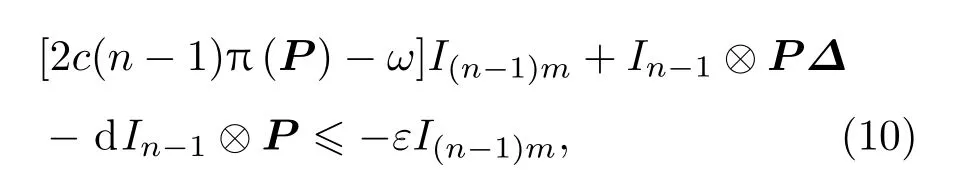
证明定义Lyapunov函数如下:

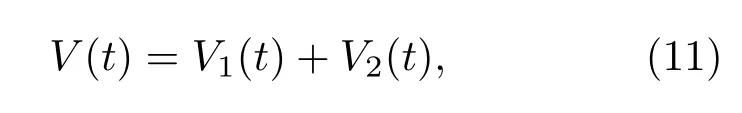
其中

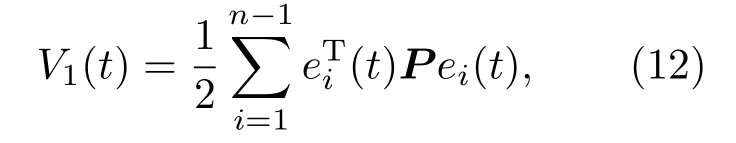
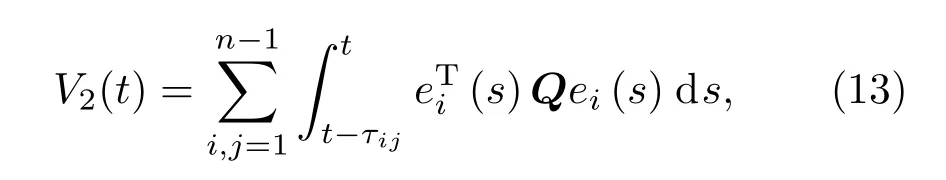
其中Q=cπ(P)In−1.

V(t)沿着系统(9)的解求导可得:

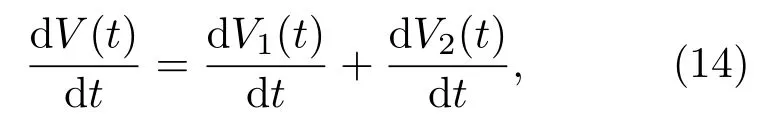
其中

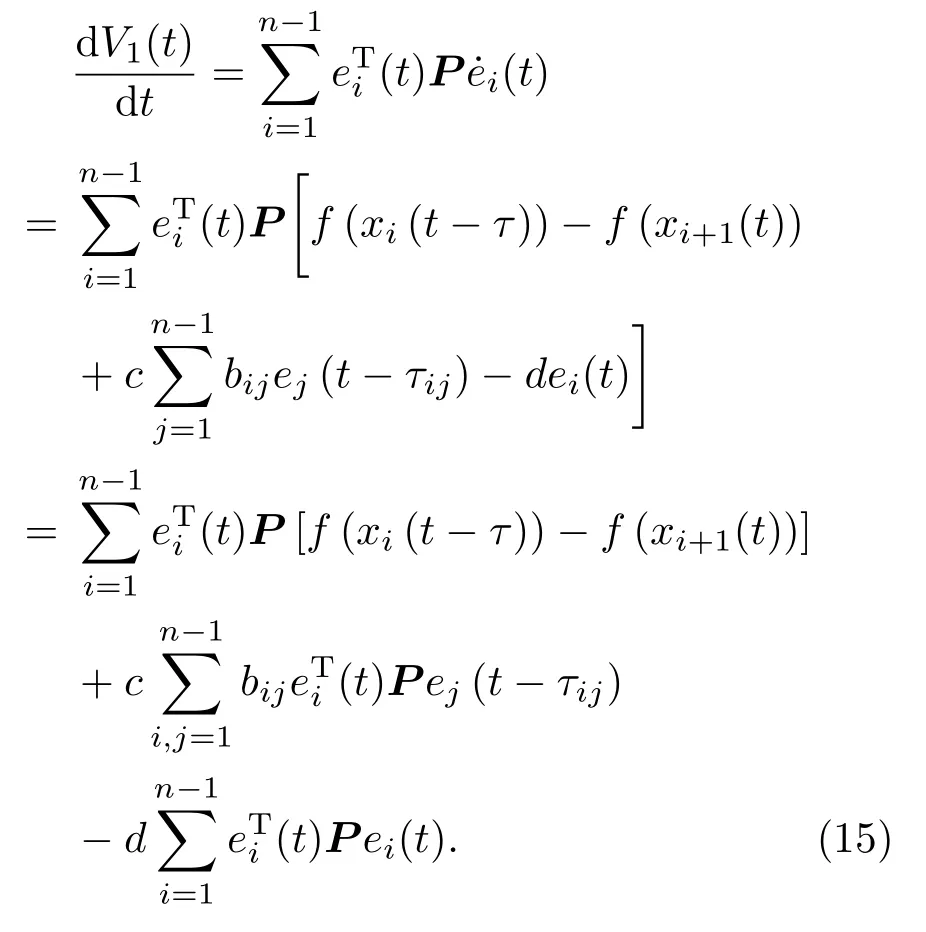
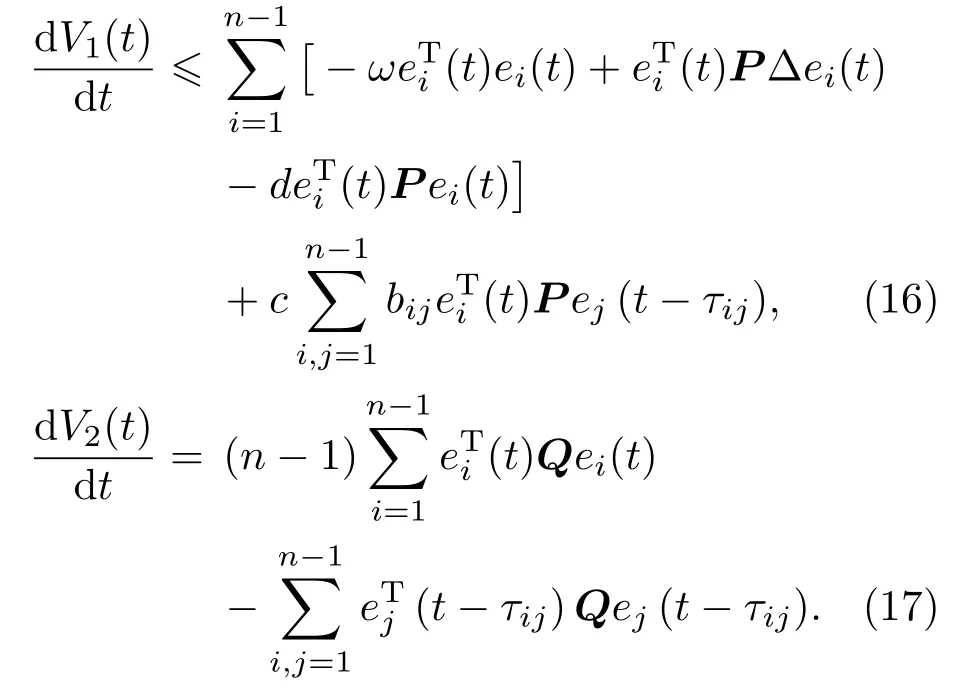
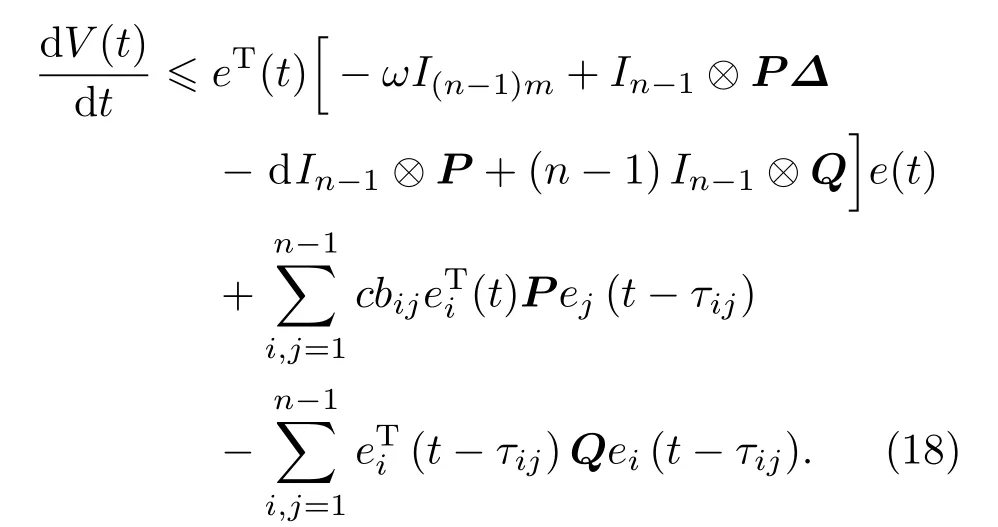
由引理1知

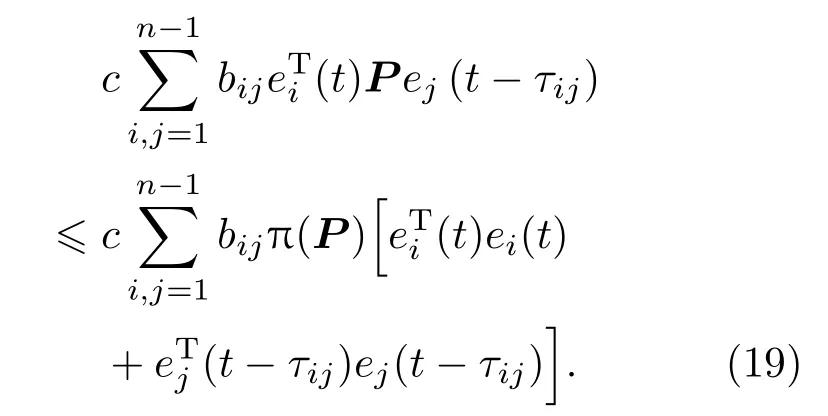
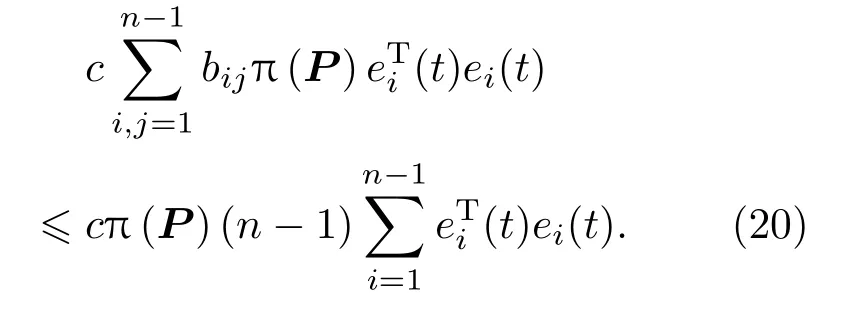
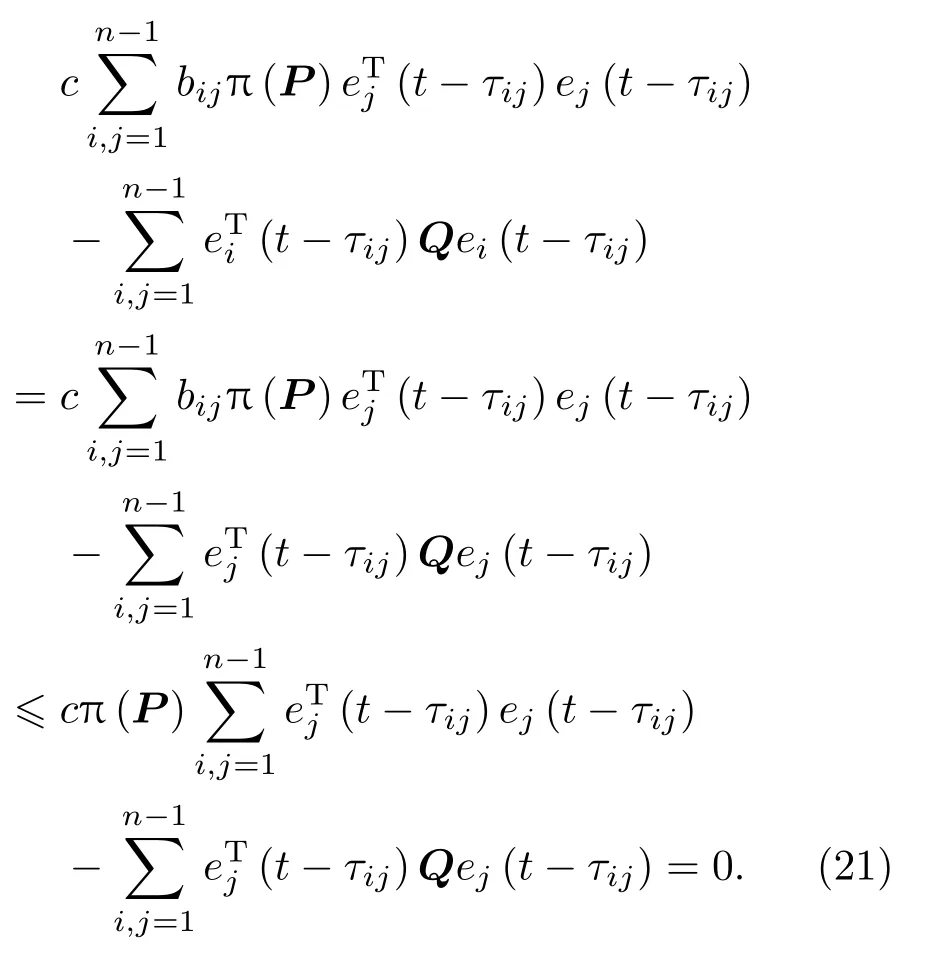
结合(18)—(21)式可知

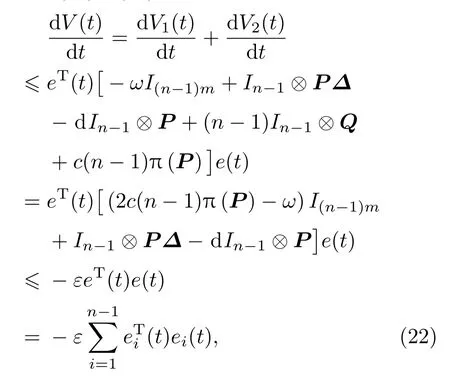
两边同时对t求积分得到

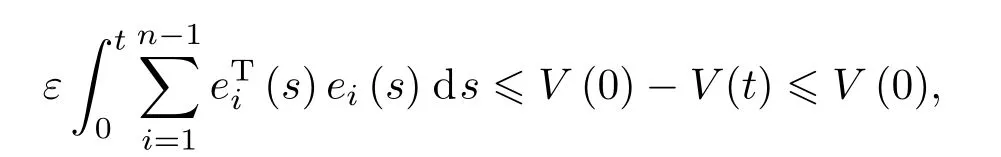
3.2 自适应反馈控制

由定理1知,总可以选取足够大的控制强度d,使得不等式(10)得以满足,从而实现网络系统(1)的接连滞后同步.但是,控制强度越大,意味着控制成本越高.为了降低控制强度,本节将采用自适应控制法来实现接连滞后同步.

定义预备函数

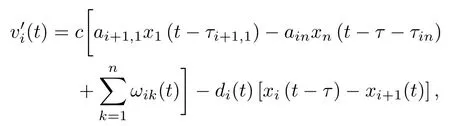
其中di(t)≥0表示时变控制强度,对于k=i,有

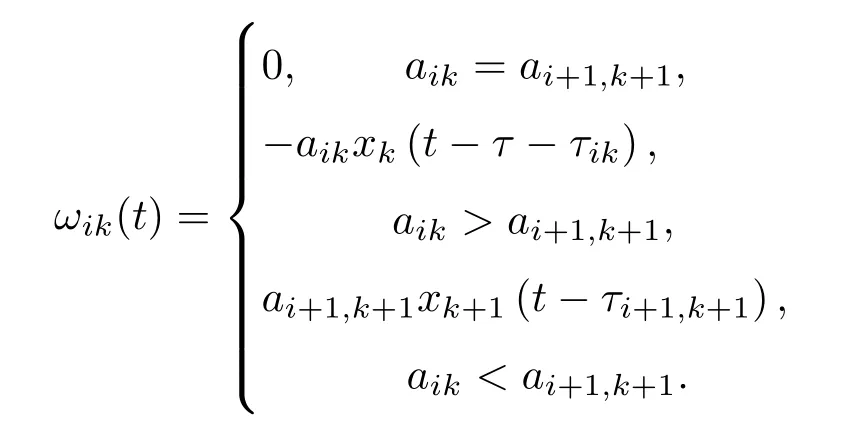
当k=i时,有

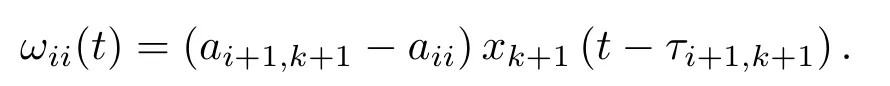
设计自适应反馈控制如下:

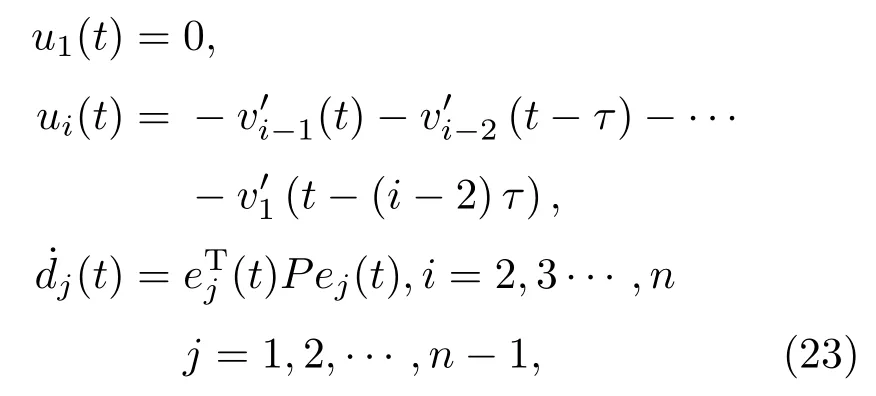
定理2设为对角矩阵,为正定对角矩阵,若那么在控制(23)下的动力学网络(1)对任何初始条件都可以实现接连滞后同步.

证明定义Lyapunov函数

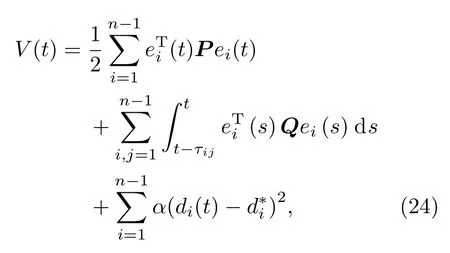
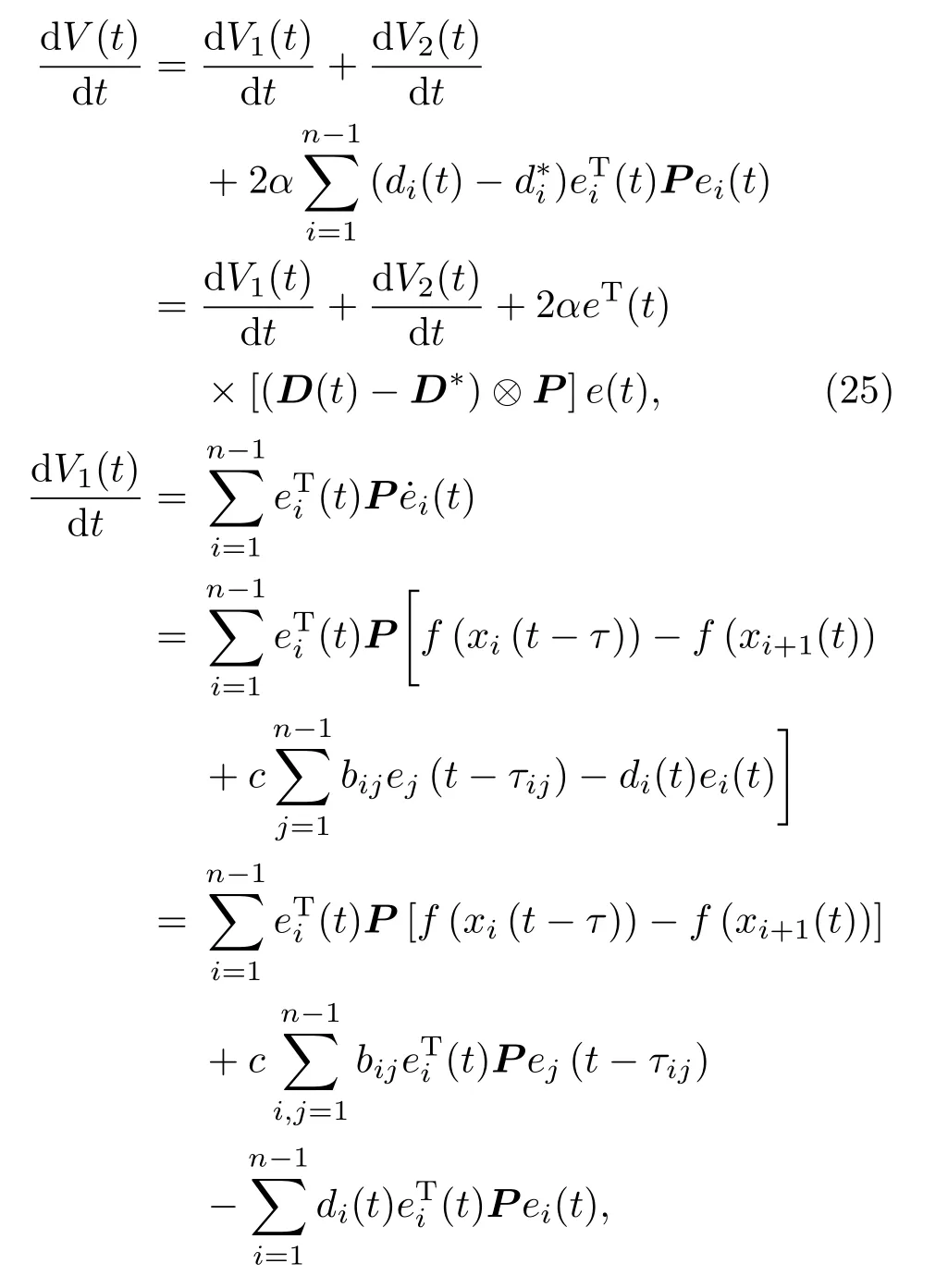
由该定理的已知条件知

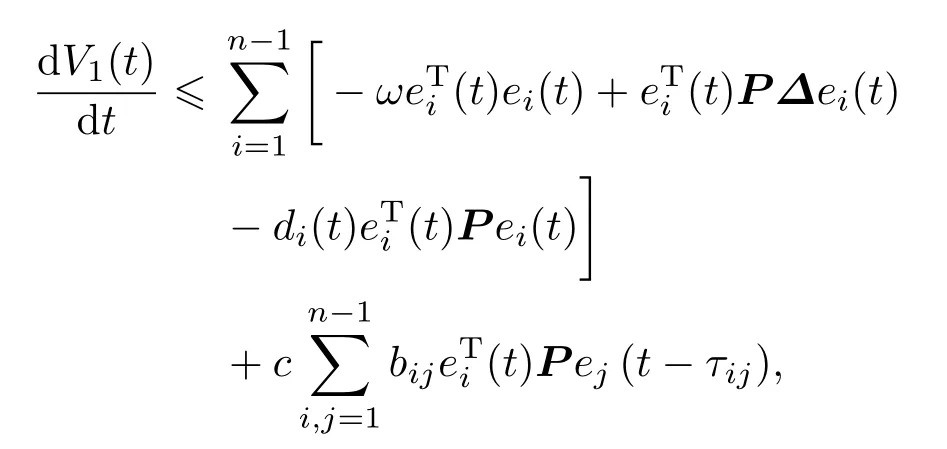
其中

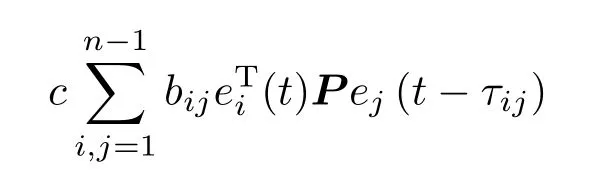
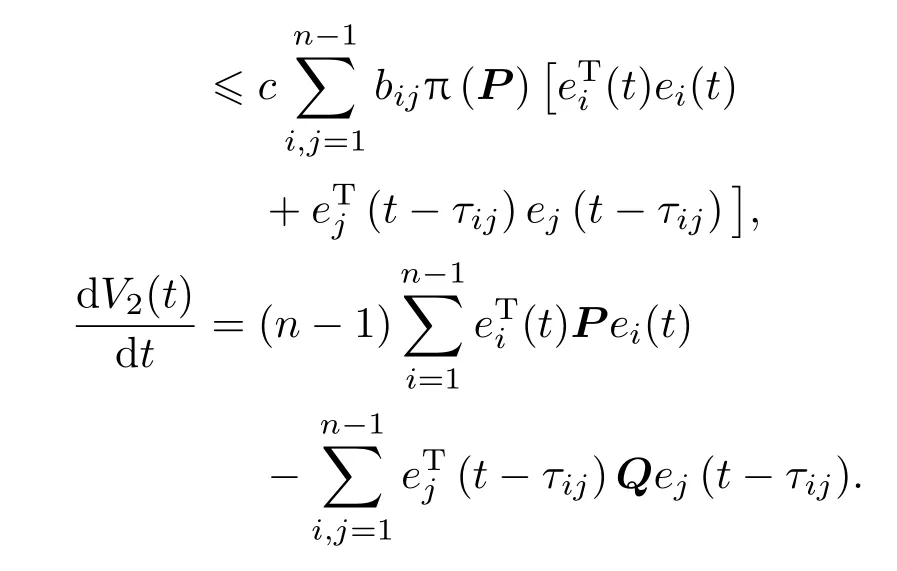
由假设1知τij=τji,从而

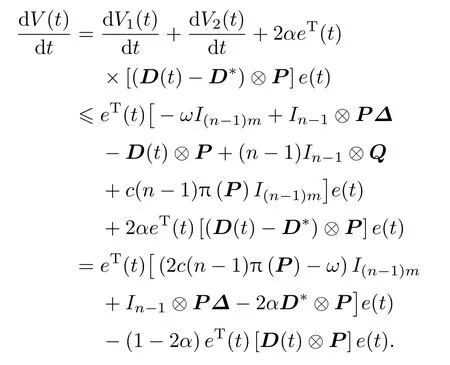
选取适当的α使得1−2α＞0,并选取适当的D∗使得

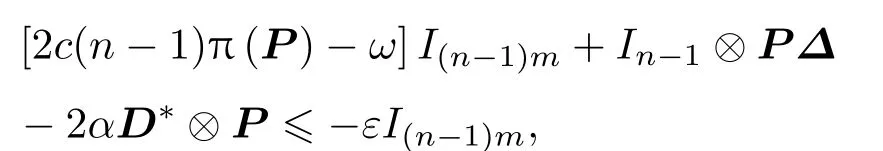
可得

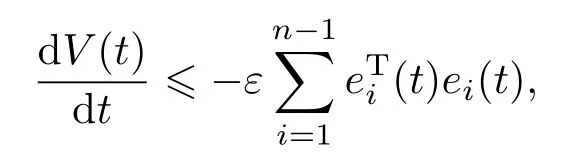
4 数值模拟

为了验证控制方法的有效性和正确性,将用具体的数值例子进行验证.

4.1 线性反馈控制

不妨选取网络(1)的局部动力学为蔡氏电路系统[20],

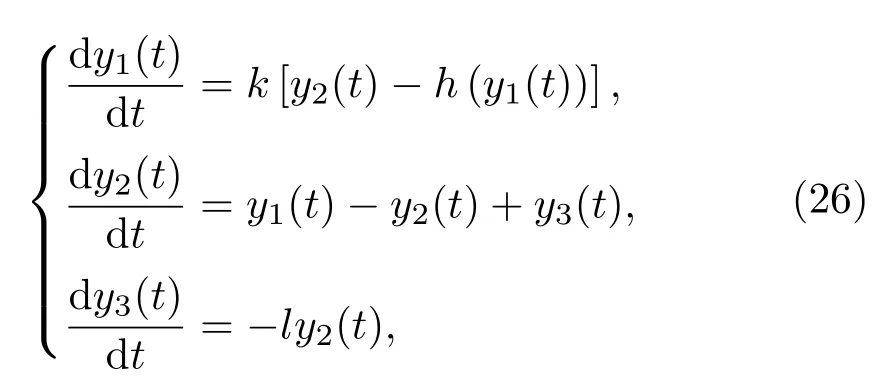
网络拓扑结构及节点编号如图1所示.不失一般性,不妨设动力学网络节点数为n=4.

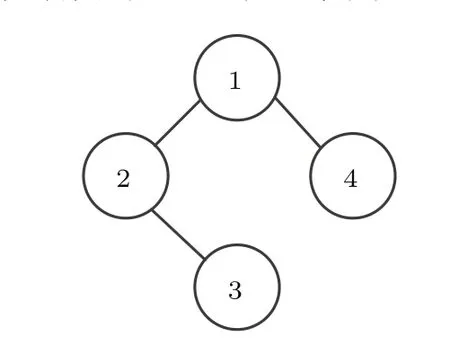
图1 节点数为4的无权无向链式网络,编码为4,1,2,3Fig.1.Unweighted and undirected Chain-shaped network with size n=4,coding 4,1,2,3.

网络结构的耦合矩阵是

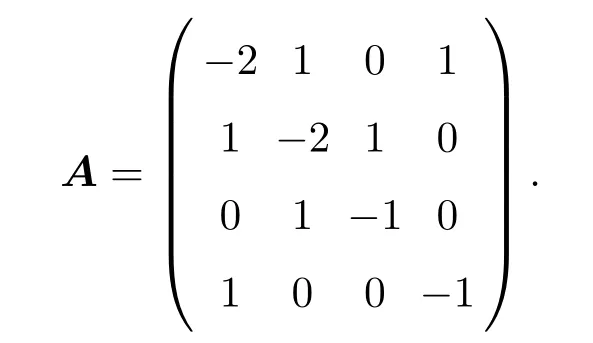
下面用线性反馈控制实现动力学网络的接连滞后同步.

根据控制(6)我们得到

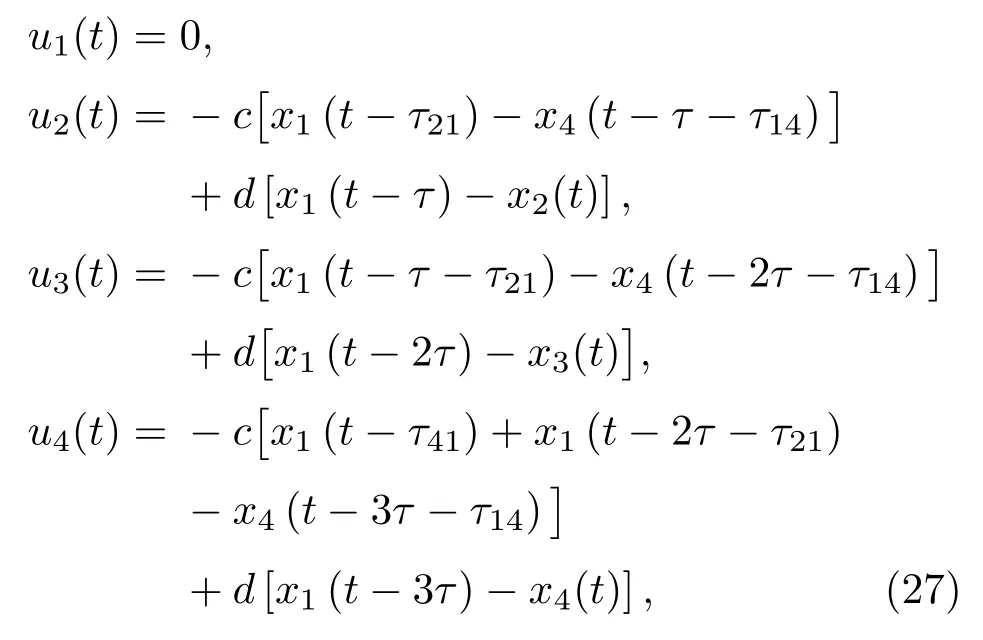
不妨选取c=0.1,由(10)式知,要使

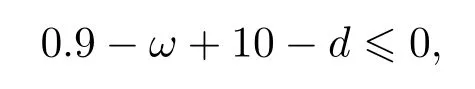
则需控制强度d≥10.2782,从而满足定理1的条件,就意味着在该控制下的动力学网络在任何初始条件下都可以实现接连滞后同步.

另外,不妨取d=14,τ=0.15,通信时滞矩阵

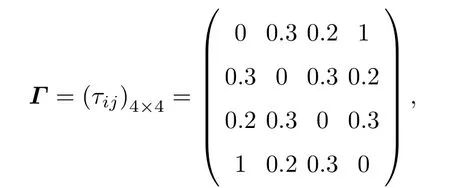
其中τ12=τ21=τ23=τ32=τ34=τ43=0.3,τ13=τ31=τ24=τ42=0.2,τ14=τ41=1. 不失一般性,类似文献[23,24],在数值模拟中,选取初始条件ϕi(t)=0.

利用MATLAB软件得到模拟结果(见图2,图3).图2给出了在线性反馈控制(6)下动力学网络的状态变量xi1,xi2,xi3的轨线,图3给出了在控制(6)下,动力学网络(1)的同步误差ei1,ei2,ei3的轨线.

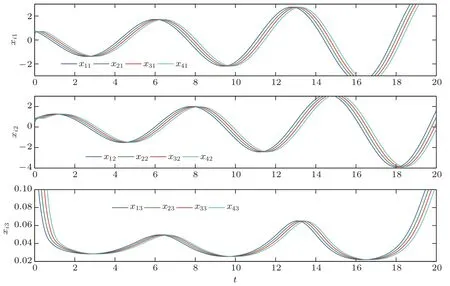
图2 在控制(6)下,动力学网络(1)的状态变量xi1,xi2,xi3的轨线,其中i=1,2,3,4,d=14.Fig.2. Trajectories of all state variables xi1,xi2,xi3of dynamical network(1)under control(6),wherei=1,2,3,4,d=14.

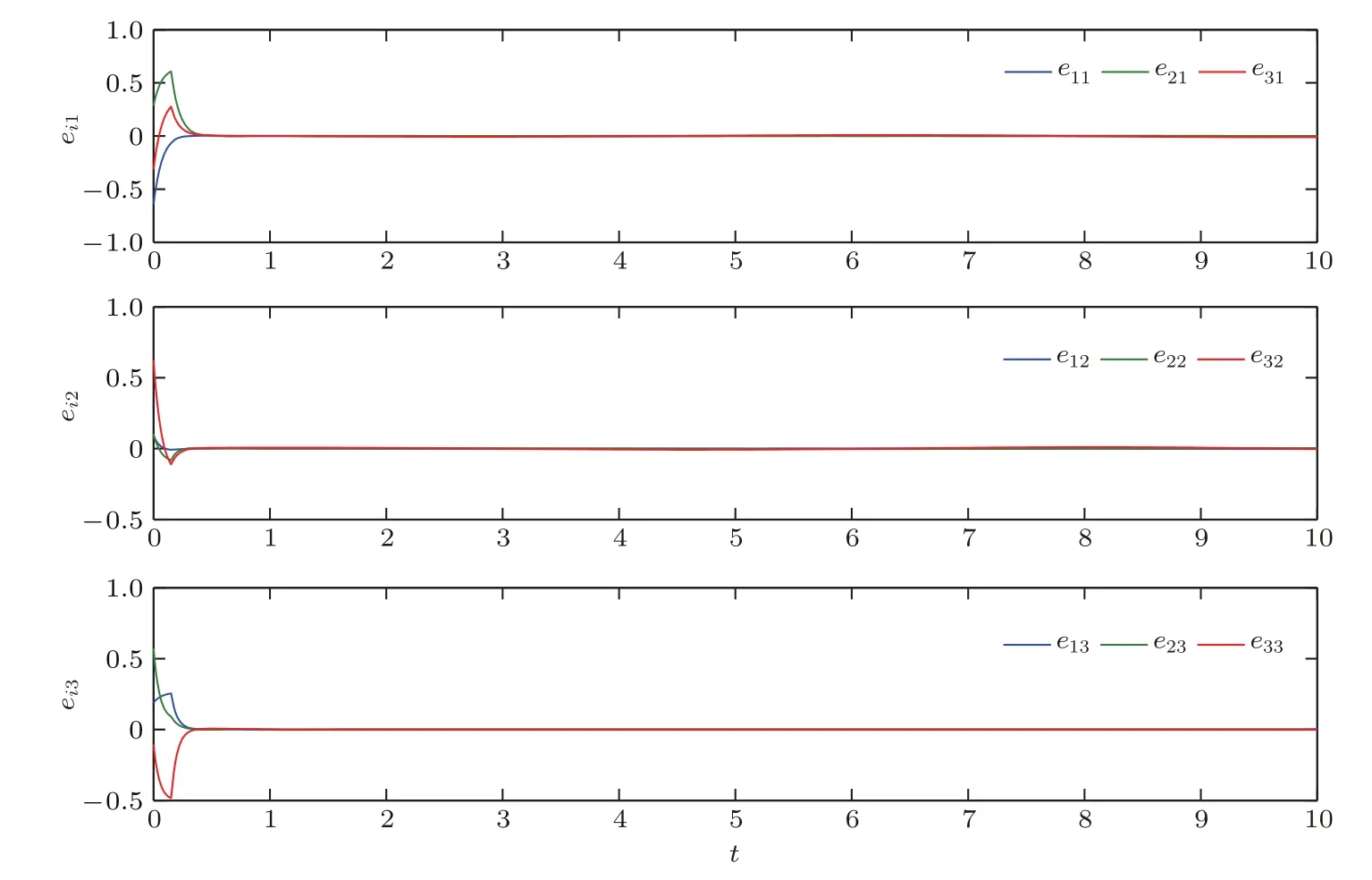
图3 在控制(6)下,动力学网络(1)的同步误差ei1,ei2,ei3的轨线,其中i=1,2,3,4,d=14Fig.3. Trajectories of SLS errors ei1,ei2,ei3of dynamical network(1)under control(6),where i=1,2,3,4,d=14.

从这些数值模拟可以看出,在线性反馈控制下动力学网络的接连滞后同步可以实现.

4.2 自适应反馈控制

与此同时,也可以在耦合矩阵不变以及其他条件都一样的情况下,用自适应反馈控制来实现接连滞后同步.

模拟结果见图4,di(t)最终都稳定了,说明实现了接连滞后同步.另外,由控制强度di(t)的轨线图可知控制强度的最大值d∗i=0.0812,说明自适应反馈控制确实可以大大降低控制强度,更加符合现实需要.

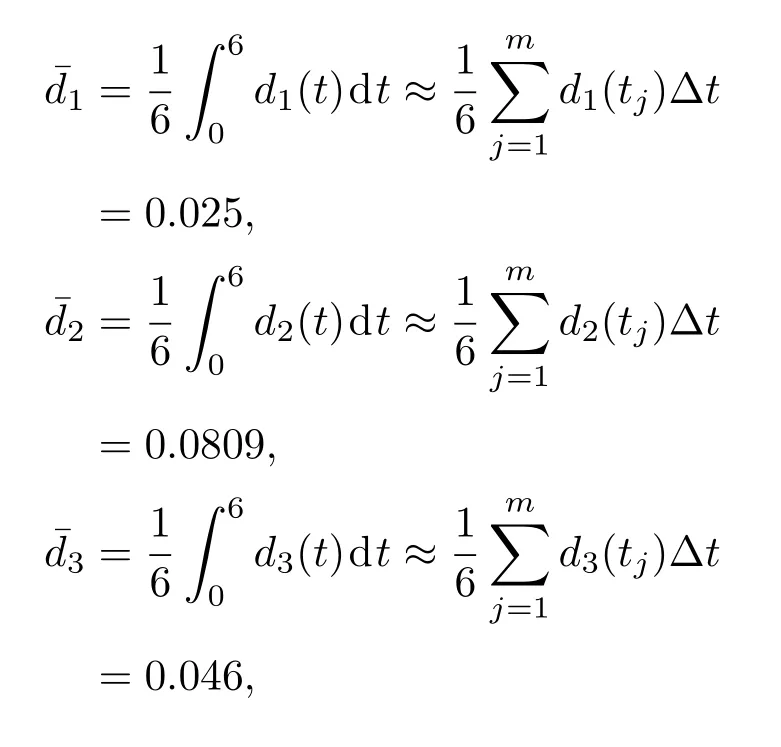
其中∆t=0.1为插值步长,m为插值的总步数,tj为插值时刻.对比发现,自适应控制的能量消耗远远小于线性反馈控制的能量消耗.

接下来,我们用自适应反馈控制实现另一个网络结构的接连滞后同步,其拓扑结构及节点编号如图5所示.

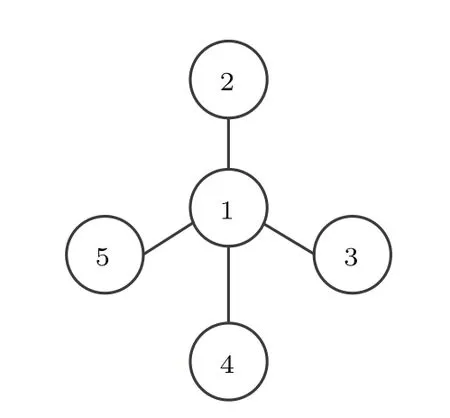
图5 节点数为5的无权无向星形网络Fig.5. Unweighted and undirected star-shaped network with size n=5.

网络结构的耦合矩阵是

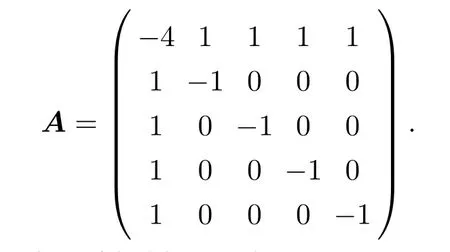
根据自适应反馈控制(23),得到

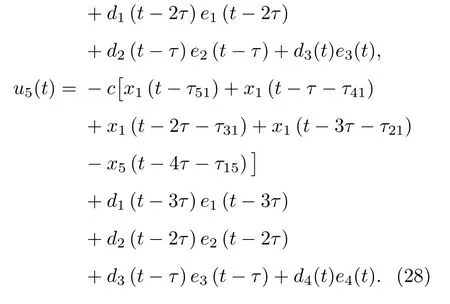
MATLAB模拟结果如图6和图7所示,图6给出了在自适应反馈控制(23)下,动力学网络(1)的同步误差ei1,ei2,ei3的轨线,图7给出了其状态变量xi1,xi2,xi3以及控制强度di(t)的轨线.

由图6可以看出,当t→+∞时,ei→0(i=1,2,3,4,5),即在控制(23)下,系统(1)的接连滞后同步可以实现.

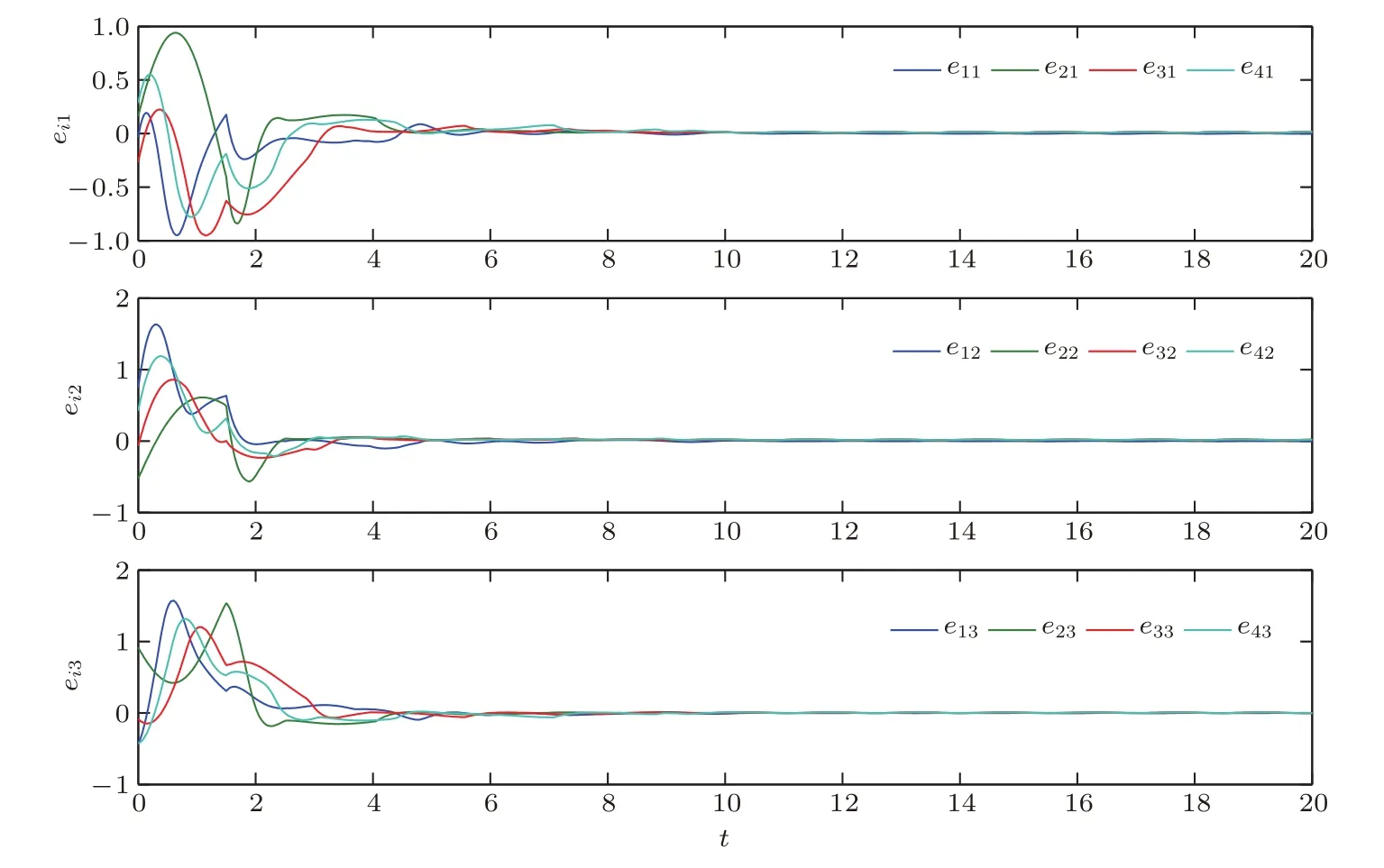
图6 在控制(23)下,动力学网络(1)的同步误差ei1,ei2,ei3的轨线,其中i=1,2,3,4,5Fig.6.Trajectories of SLS errors ei1,ei2,ei3of dynamical network(1)under control(23),where i=1,2,3,4,5.

从这些数值模拟可以看出,在自适应反馈控制下动力学网络的接连滞后同步可以实现.

5 结 论

Li等[20]依飞机按次序一一通过空中的相同位置这一现象,提出了接连滞后同步的概念.随后,考虑到节点之间的通信存在滞后现象,含一致通信时滞的网络上的接连滞后同步被Zhang等[21]进行了研究.然而由于节点的差异性,节点与节点之间的通信时滞一般来说是不一样的,所以本文提出了带有非一致通信时滞的动力学网络如何实现接连滞后同步这一问题,进而研究了它的全局稳定性.

本文设计了线性反馈控制和自适应反馈控制,实现了带有非一致通信时滞的动力学网络上的接连滞后同步,重点分析了接连滞后同步的全局稳定性,获得了同步稳定的充分条件,并且通过数值模拟验证了理论的正确性.

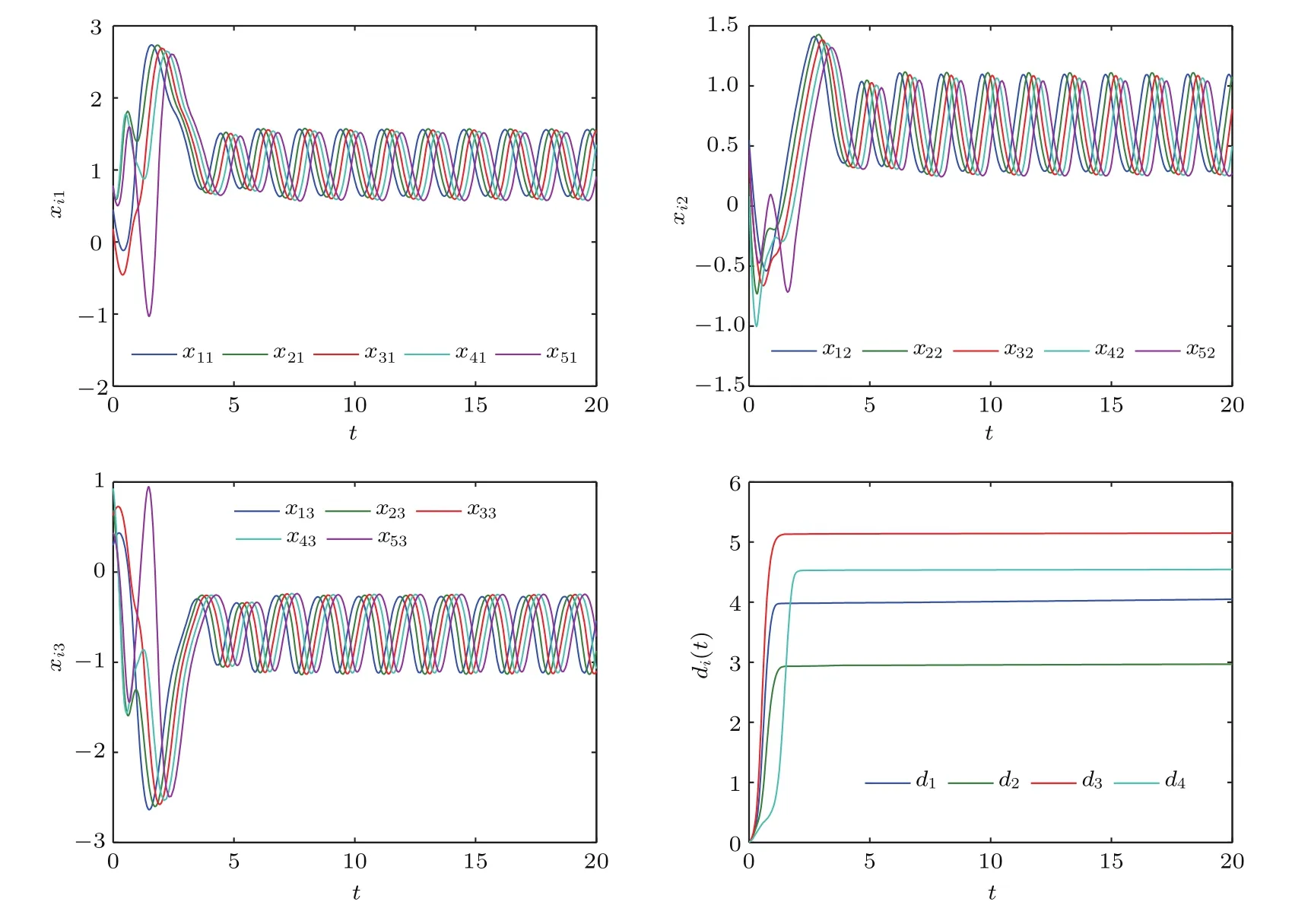
图7 在控制(23)下,动力学网络(1)的状态变量xi1,xi2,xi3以及控制强度di(t)的轨线,其中i=1,2,3,4,5Fig.7.Trajectories of all state variables xi1,xi2,xi3and di(t)of dynamical network(1)under control(23),where i=1,2,3,4,5.

值得注意的是,本文研究的模型只是局限在一个复杂网络里,使得不同节点之间实现了接连滞后同步,如何在两个甚至多个动力学网络中实现接连滞后同步,本文中设计的方法是否还适用,这是值得进一步研究的问题.

[1]Wang X F,Li X,Chen G R 2012Network Science:An Introduction(Beijing:Higher Education Press)pp3–27(in Chinese)[汪小帆,李翔,陈关荣 2012 网络科学导论(北京:高等教育出版社)第3—27页]

[2]Fang J Q,Wang X F,Zheng Z G,Bi Q,Di Z R,Li X 2007Prog.Phys.27 239(in Chinese)[方锦清,汪小帆,郑志刚,毕桥,狄增如,李翔2007物理学进展27 239]

[3]Zhao M,Zhou T,Chen G R,Wang B H 2008Prog.Phys.28 22(in Chinese)[赵明,周涛,陈关荣,汪秉宏2008物理学进展28 22]

[4]Liu J L 2012Acta Phys.Sin.61 040503(in Chinese)[刘金良2012物理学报61 040503]

[5]Feng J W,Yang P,Zhao Y 2016Appl.Math.Comput.291 52

[6]Feng J W,Li N,Zhao Y,Xu C,Wang J Y 2017Nonlinear Dyn.88 2723

[7]Wang J Y,Feng J W,Xu C,Chen M Z Q,Zhao Y,Feng J Q 2016Automatica66 155

[8]Prcora L M,Carroll T L 1998Phys.Rev.Lett.80 2109

[9]Xiao Y Z,Xu W,Li X C,Tang S F 2008Chin.Phys.B17 80

[10]Chen J,Liu Z R 2005J.Appl.Math.Mech.26 1132

[11]Li X W,Zheng Z G 2007Commun.Theor.Phys.47 265

[12]Shahverdiev E M,Sivaprakasam S,Shore K A 2002Phys.Lett.A292 320

[13]Li X,Chen Y 2007Commun.Theor.Phys.48 132

[14]Dai H,Jia L X,Zhang Y B 2012Chin.Phys.B21 120508

[15]Feng J W,Wu G,Zhang W Q,He L 2009J.Shenzhen Univ.Sci.Engin.26 36(in Chinese)[丰建文,吴耿,张维强,何玲2009深圳大学学报理工版26 36]

[16]Wu W,Chen T P 2009Physica D238 355

[17]Yang X S,Zhu Q X 2011Nonlinear Anal.RWA12 93

[18]Wu X J,Lu H T 2012Commun.Nonlinear Sci.Numer.Simulat.17 3005

[19]Pal S,Sahoo B,Poria S 2013Phys.Scr.87 45011

[20]Li K Z,Yu W W,Ding Y 2015Nonlinear Dyn.80 421

[21]Zhang X J,Wei A J,Li K Z 2016Chin.Phys.B25 038901

[22]Yu W W,Chen G R,Cao M,Kurths J 2010IEEE Trans.Syst.Man Cybern.B:Cybern.40 881

[23]Mei J,Ren W,Chen J,Ma G F 2013Automatica49 1723

[24]Xie Y Y,Wang Y,Ma Z J 2014Acta Phys.Sin.63 040202(in Chinese)[谢媛艳,王毅,马忠军2014物理学报63 040202]

[25]Chen T P,Liu X W,Lu W L 2007IEEE Trans.Circuits Syst.I54 1317

[26]Li K Z,Zhou J,Yu W W 2014Appl.Math.Model.38 1300

[27]Tao G 1997IEEE Trans.Automat.Control42 698

[28]Fang B R,Zhou J D,Li Y M 2013Matrix Theory(Beijing:Tsinghua University Press)pp350–352(in Chinese)[方保镕,周继东,李医民2013 矩阵论 (北京:清华大学出版社)第350—352页]