分布损耗加载回旋行波管多模稳态注波互作用理论与比较证实∗

罗积润 唐彦娜 樊宇 彭澍源薛谦忠

1)(中国科学院电子学研究所,中国科学院高功率微波源与技术重点实验室， 北京 100190)

2)(中国科学院大学,北京 100039)

3)(中国电子信息技术研究院,北京 100041)

1 引 言

回旋管是一种基于相对论效应的快波器件,能够在毫米波长范围产生几百千瓦甚至兆瓦量级的输出功率,已经在核聚变等离子体加热[1,2]、高分辨率雷达[3]以及加速器[4]等科学和技术领域得到广泛应用.类似于传统真空微波器件,回旋管家族包括回旋振荡管、回旋行波管、回旋速调管和回旋返波管[5−9]等.作为一种波导式互作用结构,回旋行波管具有很宽的带宽,但很容易受到高次模式的绝对不稳定性振荡、回旋返波振荡以及因输入输出不匹配引起的反射振荡等竞争干扰[4,10−12].因此,模式的选择和抑制对保持回旋行波管的稳定工作非常重要.

许多理论和实验工作已经用于研究回旋行波管中几何和电参量变化对振荡的影响以改善工作的稳定性[13−17].一种改善稳定性的有效方法是加载分布损耗[18].台湾国立清华大学通过分布损耗加载实验证实了一个Ka波段TE11模基波回旋行波管能够在93 kW饱和输出峰值功率、26.5%效率、70 dB增益和8.6%带宽条件下稳定工作[19].美国海军实验室通过分布损耗周期加载实现了一个中心频率34 GHz,TE01模基波回旋行波管在峰值功率130 kW,效率18%,增益47.5 dB、带宽约1 GHz情况下的稳定工作[11].我国电子科技大学通过非均匀周期介质加载使一个W波段、TE01模基波回旋行波管能够在峰值功率112 kW、效率23.3%、增益69.7 dB,带宽4.2%条件下稳定工作[20].

相关分布损耗加载改善稳定性的分析通常主要是利用单模理论和粒子波包(PIC)模拟.文献[19]曾经对这种单模理论进行了讨论.使用这种单模理论可以对管子设计的结构和电参量进行初步选择,而PIC模拟是预言设计特性的基本手段.不过,单模理论和PIC模拟存在不足,单模理论假定回旋行波管中只有一个模式处于放大或振荡状态,这无法分析那些振荡模式与工作模式之间的相互影响,但使用商业软件(CST,Magic,etc.)的PIC模拟却要耗费太多的计算时间.

影响放大器稳定性最严重的因素是寄生振荡.为了分析振荡对工作模式的影响,必须假设多个模式同时存在.文献[21,22]曾经使用时域方法讨论过回旋行波管中多频和多模注波互作用,但这种方法的计算过程需要跟踪数万个带电粒子.在忽略导引中心运动的条件下,文献[23,24]基于哈密顿算子获得了回旋行波管的多模稳态分析公式.不过,这些公式不能够适用于正向波处于大信号的情况.文献[25]发展的多模稳态理论能够用于研究返波自激振荡对处于大信号状态的正向波的影响.不过,文献[25]假设返波的幅度仅仅是小信号状态,于是返波对电子的影响被认为是小的扰动.文献[26]也讨论过多模同时存在对稳定性的影响,并且获得了与文献[19]实验有合理一致性的结果.不过,模型中加载的损耗被认为是波导表面电导率的减少,这在实际工程应用中不容易实现.本文讨论的回旋行波管注波互作用多模稳态理论,可以分析有损均匀介质加载(UDL)和周期介质加载(PDL)波导互作用结构中工作模式和返波振荡模式之间的相互影响.不过,我们曾经在文献[27]中详细讨论过返波振荡的抑制和工作模式稳定放大过程,本文主要通过理论计算与实验和软件模拟结果的比较,证实理论的合理性.

2 理论模型和公式

图1给出了两种形式的分布损耗加载波导互作用电路模型,UDL波导和PDL波导.互作用电路包括损耗加载线性段和无加载非线性段.UDL波导是在线性段均匀加载损耗材料,PDL波导是在线性段损耗材料通过金属环等间隔隔开.在这两种结构中,波导的半径为rw,损耗层厚度为∆r.PDL结构中,L是周期,b是每个周期中损耗材料的长度.

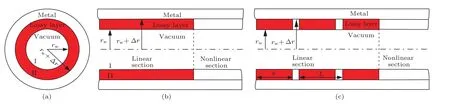
图1 损耗加载波导结构图 (a)横截面图;(b)UDL模型轴向剖面图;(c)PDL模型轴向剖面图Fig.1.Structures of the loss-loaded cylindrical waveguides:(a)The transverse sectional view;(b)the longitudinal view of UDL cylindrical waveguide;(c)the longitudinal view of PDL cylindrical waveguide.

本文的理论是在同时考虑多个模式与电子之间能量交换的条件下,获得图1模型注波互作用的一般公式.基于如下基本假设,该理论由麦克斯韦方程组和带电粒子运动方程经过数学推导得到:1)高频场的横向分布不受电子存在的影响,其振幅只在轴向发生变化;2)不考虑电子之间的空间电荷力.

2.1 均匀损耗加载圆波导中高频场分布

以均匀损耗波导为例对高频场演化方程进行分析.将波导结构划分为两部分,区域I为真空区域,区域II为损耗加载区域,其中真空区域的介电常数和磁导率为εI和µI,介质区域的介电常数和磁导率为εII和µII.对于角向不均匀的高频场,介质波导中的模式为混合模式.本文所考虑的模式仅为TE模式或者混合模式中的TE分量(经计算混合模式中TE分量达到95%以上).模式仍采用TEmn方式命名.场分量表达式可以描述为:

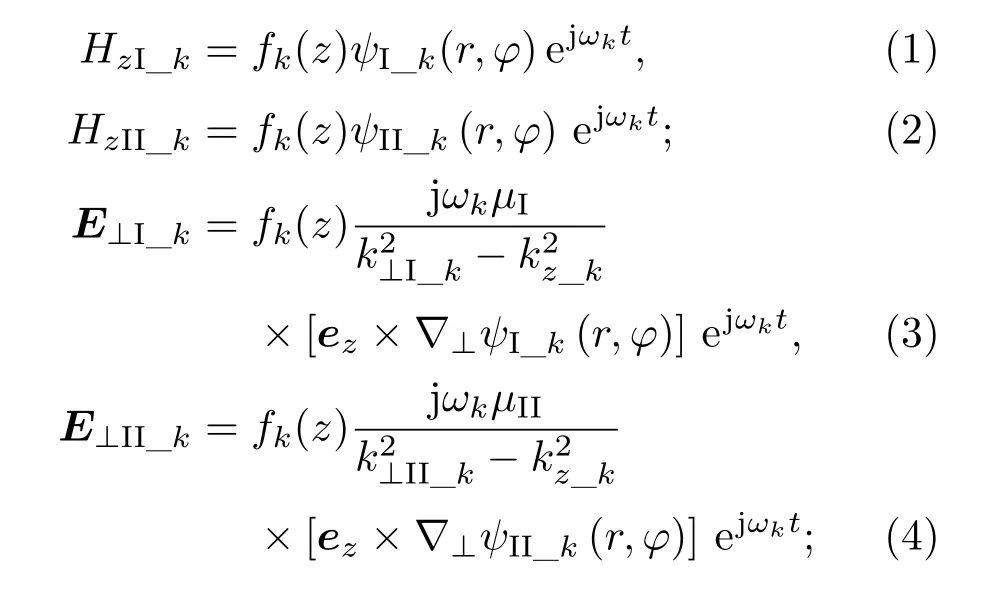
式中ωk为第k个模式的角频率,fk(z)为第k个模式的轴向分布,ψI_k(r,φ)和ψII_k(r,φ)为k个模式的横向分布.波导中真空区域和介质区域的波数满足下列条件:

其中,kz_k为第k个模式的轴向波数,k⊥I_k为第k个模式在区域I的截止波数,k⊥II_k为第k个模式在区域II的截止波数.考虑多个TE模式同时存在的情况,高频场轴向分量可描述为各个模式的叠加:

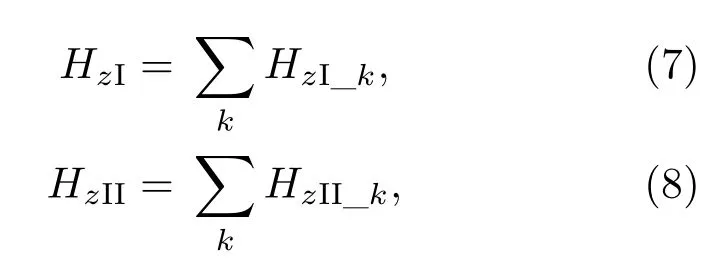
基于麦克斯韦方程组得到互作用系统中

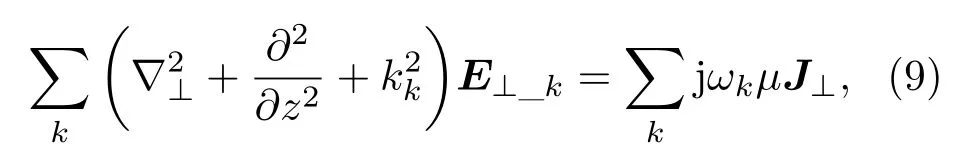
其中,电流分布为

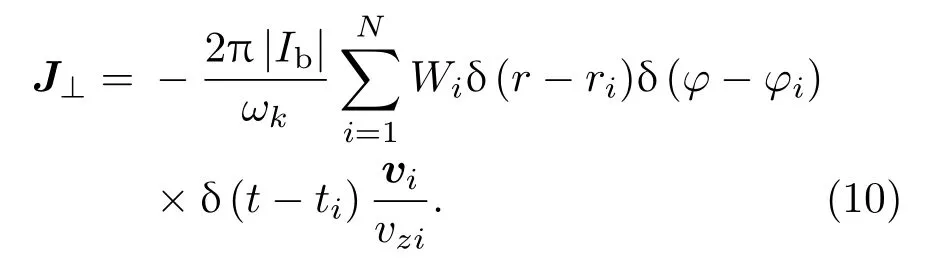
将(10)和(11)式代入(9)式并化简,得到高频场演化方程

在(12)式两边同时乘以

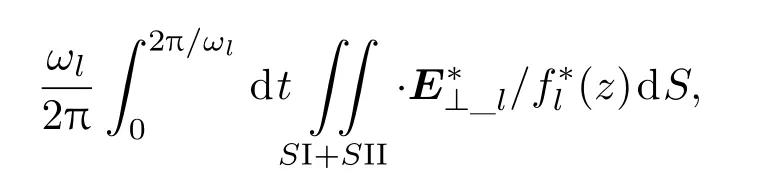
式中左边的实部可以计算为

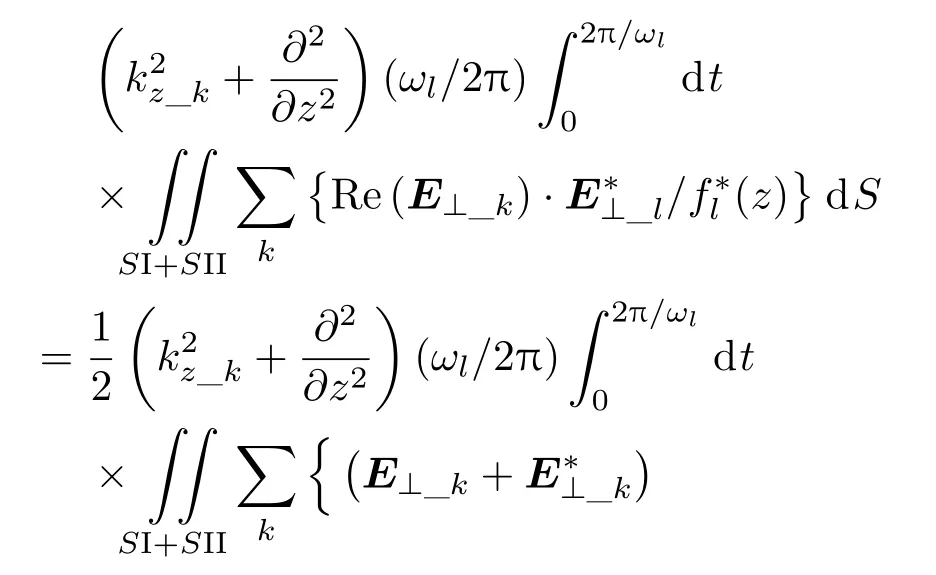
由于横向分布函数具有正交性,因此

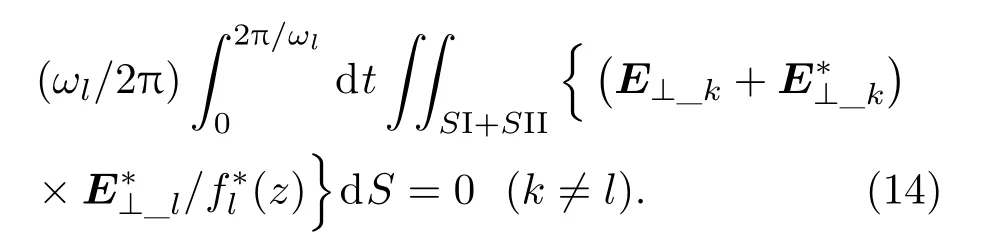
当k=l时,定义结构因子

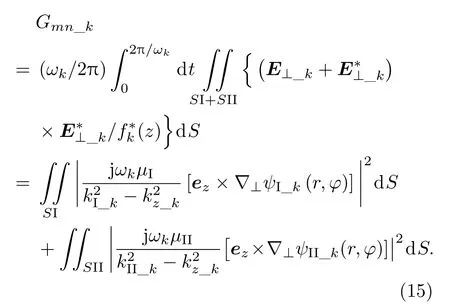
根据(14)和(15)式可以得出,当k=l时,(12)式可以简化为

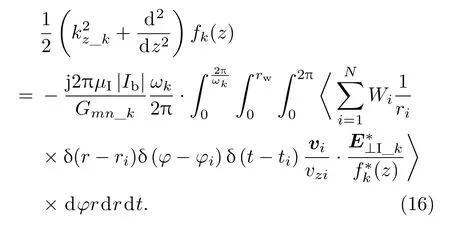
2.2 不同情况下的场演化方程

1)光滑波导中的高频场

在光滑波导(非线性区域)的情况下,没有损耗加载,只需考虑真空区域I的影响,此时对应的轴向传播常数为

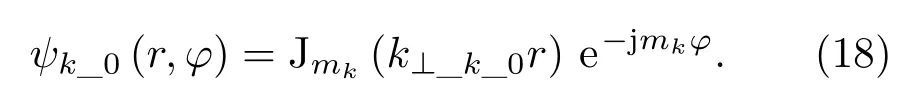
(15)式中的结构因子为

(16)式中的高频场演化方程简化为

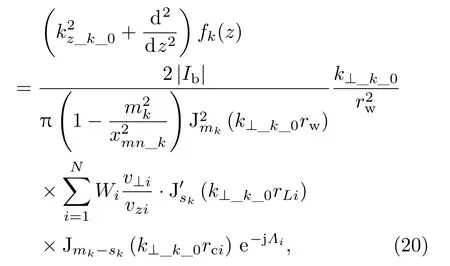
其中,相位因子Λi=ωkti−skθi−(mk−sk)φci,ωk为角频率,θi为回旋角,φci导引中心角,ti为进入时间.

2)均匀损耗加载波导中的高频场

假如波导被分布损耗加载,传输常数变成一个复数,均匀介质加载波导中的本征值能够通过以下色散方程求解[28]:

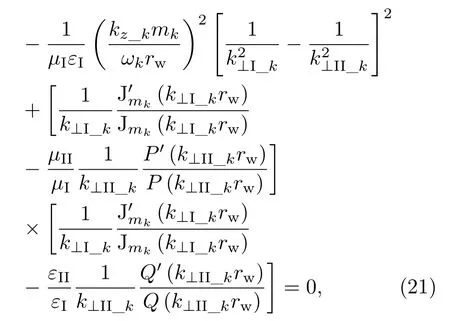
其中

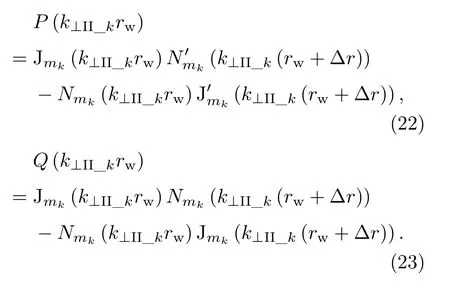
Nmk(k⊥II_kr)为第二类贝塞尔函数.按照文献[29],损耗正切定义为

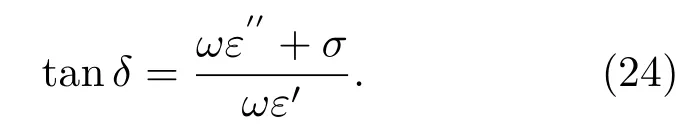
根据(24)式不仅可以计算介质带来的损耗,还可以将导电损耗一并进行考虑.

在区域I和区域II,横向场分布可以表述为:

式中,

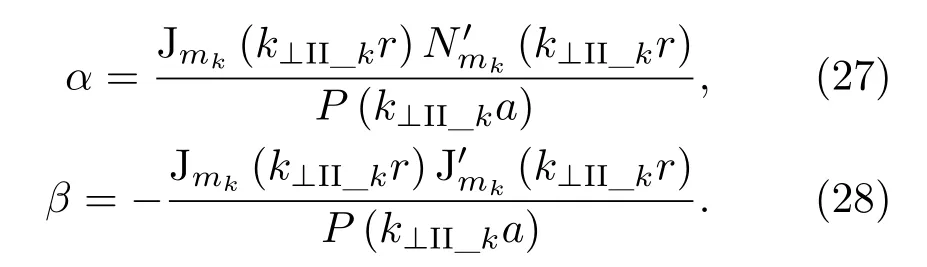
分别将方程(25)和(26)代入方程(15)和(16),获得均匀加载介质波导中纵向场分布演化方程为

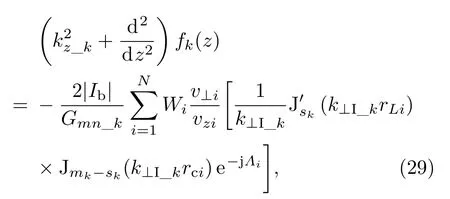
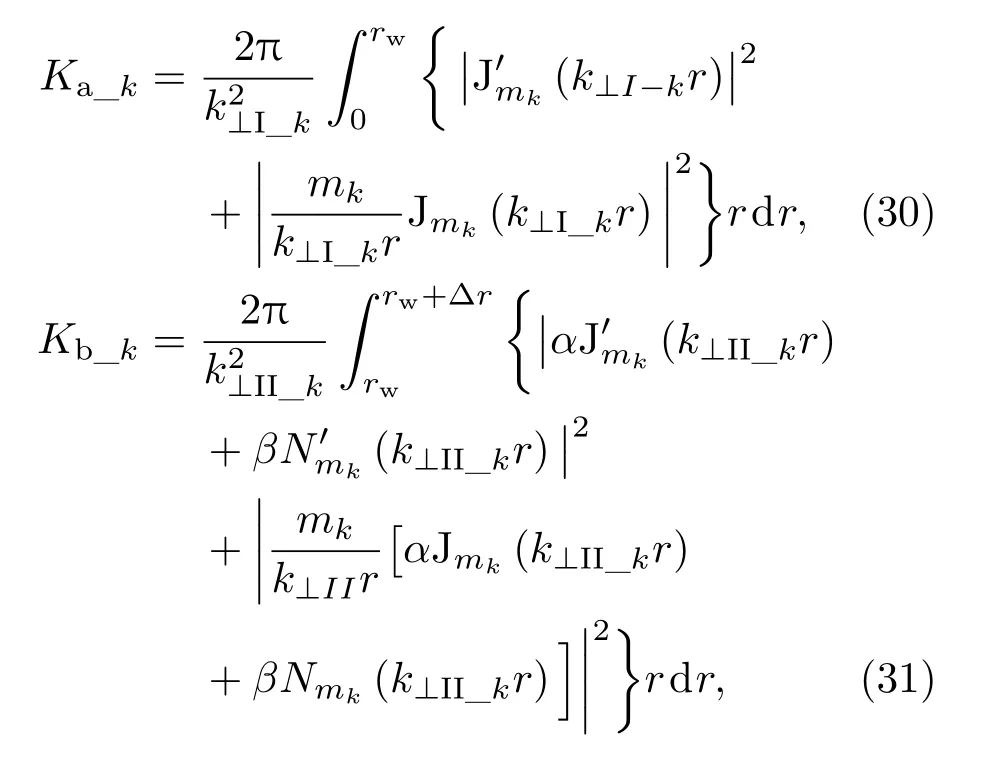
Ib为注电流,rLi为拉莫半径,rci为导引中心半径,v⊥i为横向速度,vzi为轴向速度.

3)周期介质损耗加载波导中的高频场

利用Floquet定理,在周期介质加载波导真空区域I中场可以表示为Bloch谐波分量的叠加求和,在介质区II场则可以写为驻波的叠加求和[30].对于感兴趣的模式而言,电磁能量主要集中在真空区域I[31].因此,高频场演化方程可采用(29)式,只是对于周期损耗加载模型,由于介质区域的场可以忽略,结构因子简化计算为Gmn_k=Ka_k.

2.3 电子动力学

在互作用区电子运动遵守相对论电子动力学方程:

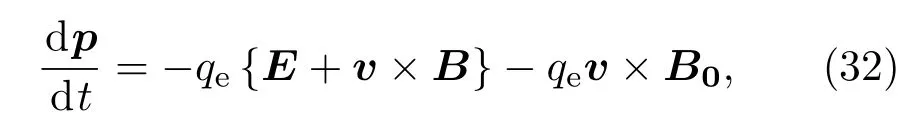
其中p=meγv,v为电子的速度,γ为相对论因子,qe为电子电荷量.B0是磁通量密度,可以表示为

结合本构关系B=µH、场表达式(25)和(33)以及电子动力学方程(32),受多模场共同作用的电子状态演化方程可以表示为:

式中的物理量分别是轴向动量pz、横向动量pt、电子引导中心半径rc、电子引导中心角ϕc以及电子到达某一轴向位置z的时刻t.

结合高频场幅度演化方程(29)以及电子运动状态方程(34),构成了分布式损耗加载波导中的自洽非线性多模稳态理论基本方程.

3 计算结果与比较

由于作者曾经在文献[27]中详细讨论过回旋行波管中寄生模式振荡和抑制、零驱动稳定、工作模式稳定放大等过程,本文仅仅为了强调验证理论的合理性.利用本文理论编写的相应计算程序,基于美国海军实验室和中国科学院电子学研究所的Ka波段TE01模回旋行波管实验参数和数据以及W波段TE01模回旋行波管Magic软件模拟设计参数和数据,与理论模拟设计数据进行比较.

3.1 与美国海军实验室(NRL)结果的比较[11]

表1给出了美国海军实验室设计的Ka波段、周期损耗加载TE01模基波工作回旋行波管的几何和电参数.图2给出了不同速度离散下本文理论计算和NRL实验测试结果的比较.NRL测试得到的输出最大峰值功率130 kW(34 GHz),对应增益为47.5 dB、效率为18%,3 dB带宽大约为1.0 GHz.NRL报道的电子速度离散为8%—10%.理论计算时分别设置电子速度离散为8%,9%和9.6%,当电子速度离散取值为9.6%时,理论计算得到输出最大峰值功率为127 kW(34.09 GHz),对应增益为47.4 dB、效率17.6%,3 dB带宽约为1.01 GHz.可以看出,速度离散取值9.6%得到的结果与实际测试结果大致符合.在频率34 GHz附近,本文多模理论计算结果与测试结果相差最大,实际测试结果约为127 kW,理论计算得到输出为118 kW,理论计算与实验测试的相对误差为8.5%.理论计算了速度离散为9.5%和9.7%的情况,计算结果与实验测试结果差异大于速度离散为9.6%的情况,实际速度离散应该介于9.5%—9.7%.

表1 NRL设计回旋行波管基本参数表Table 1.Parameters of gyro-TWT designed by NRL.

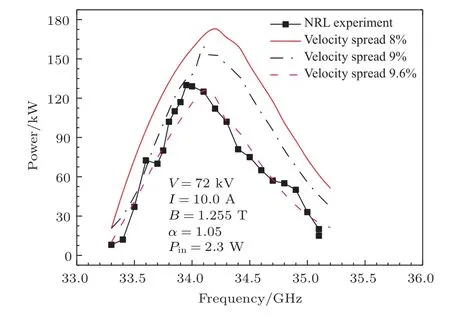
图2 理论计算结果与NRL测试结果比较Fig.2.Comparison between multimode theory results and NRL measured experimental results under the same parameters.

3.2 与中国科学院电子学研究所(IECAS)实验结果的比较[32]

表2给出了中国科学院电子学研究所设计的Ka波段、周期损耗加载TE01模基波工作回旋行波管的几何和电参数.基于这些工作参数、本文的理论计算程序以及中国科学院电子学研究所研制的回旋行波管实验数据,图3给出了对不同速度离散的理论计算和实验输出功率随频率变化的结果比较.

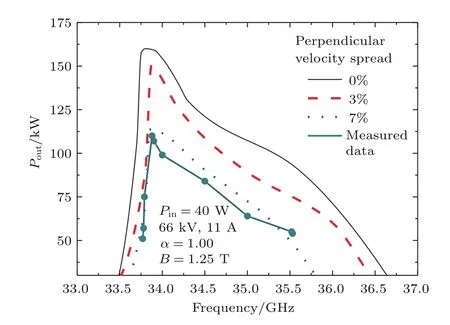
图3 理论计算结果与中国科学院电子学研究所测试结果比较Fig.3.Comparison between multimode theory results and IECAS measured experimental results under the same parameters.

表2 中国科学院电子学研究所设计回旋行波管基本参数表Table 2.Parameters of gyro-TWT designed by IECAS.

图3中曲线表明,理想情况下(速度离散为0),饱和输出为160 kW,对应增益为36.02 dB,3 dB带宽为2.19 GHz;速度离散为3%情况下,饱和输出为150.82 kW,3 dB带宽为1.78 GHz;速度离散为7%情况下,饱和输出为110 kW(33.88 GHz),3 dB带宽为1.72 GHz.实际测试显示输出峰值为110 kW(33.88 GHz),3 dB带宽为1.75 GHz,中心频率为34.65 GHz.实验结果与速度离散取值为7%时的计算结果基本相符.此时对应的速度离散值高于EGUN仿真预测的电子速度离散(3%—5%),两者的差异可能是由于机械加工和装配过程中的误差引起.

3.3 与Magic软件仿真结果的比较

3.1和3.2节中的比较都是针对Ka波段进行的.为了能够在更高频段进行比较,作者曾经尝试寻找合适的实验数据,不过目前除了文献[20]介绍的非均匀周期介质加载W波段、TE01模基波回旋行波管结果外,没有更高频段采用均匀周期加载的实验结果发表.为了进一步证实理论的合理性,作者利用本文理论设计了一个W波段、TE01模基波回旋行波管,同时将其与Magic软件模拟仿真结果进行比较,具体参数见表3.

图4给出了W波段、TE01模基波回旋行波管理论设计与Magic软件仿真结果的比较.从图4可以看出,当输入功率为40 W时,本文理论计算得到在频率为94.5 GHz时饱和输出功率为112 kW,增益为34.28 dB,3 dB带宽约为4.1 GHz;对应Magic仿真得到饱和输出功率为107.6 kW,增益为34.11 dB,3 dB带宽3.9 GHz.两种计算的结果,无论是功率还是带宽,最大相对误差大约都在5%左右.

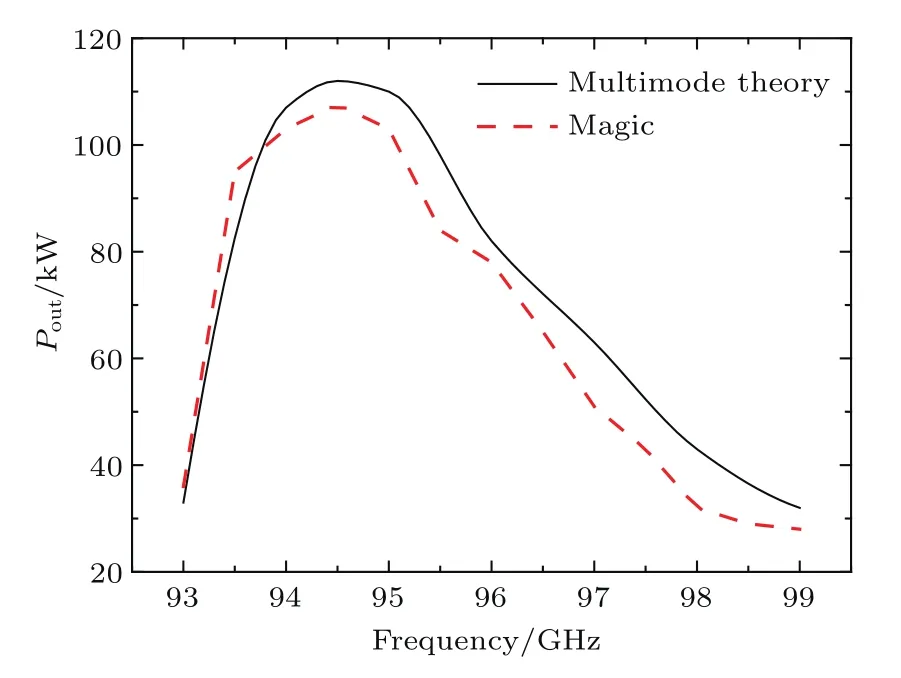
图4 W波段、TE01模基波回旋行波管理论设计与Magic软件仿真结果比较Fig.4.Comparison between multimode theory results and simulated results with Magic code under the same parameters.

表3 W波段、TE01模基波回旋行波管设计基本参数表Table 3.Design parameters of W band TE01fundamental mode gyro-TWT.

4 总 结

本文建立了一种均匀或周期介质损耗加载回旋行波管注波互作用多模稳态理论,可以适用于介质损耗和电导率损耗两种情况.利用这种理论,在相同参数条件下,对NRL和中国科学院电子学研究所设计的Ka波段、TE01模基波回旋行波管以及Magic软件仿真设计的W波段、TE01模基波回旋行波管注波互作用进行了分析计算.结果表明,理论与实验及仿真结果具有合理的一致性.

[1]Luce T C 2002IEEE Trans.Plasma Sci.30 734

[2]Kalaria P C,Kartikeyan M V,Thumm M 2014IEEE Trans.Plasma Sci.42 1522

[3]Thumm M 2005Int.J.Infr.Millim.Waves26 483

[4]Chu K R 2004Rev.Mod.Phys.76 489

[5]Thumm M 2016State-of-the-Art of High Power gyro-Devices and Free Electron Masers.Update 2015(KIT Scienti fi c Reports;7717)Karlsruhe(Germany:Wissenschaftliche Berichte FZKA)

[6]Bratman V,Glyavin M,Idehara T,Kalynov Y,Luchinin Y,Manuilov A,Mitsudo S,Ogawa I,Saito T,Tatematsu Y,Zapevalov V 2009IEEE Trans.Plasma Sci.37 36

[7]Flyagin V A,Gaponov A V,Petelin M I,Yulpatov V K 1977IEEE Trans.Microwave Theory and Techniques25 514

[8]Parker R K,Abrams R H,Danly B G,Levush B 2002IEEE Trans.Microwave Theory and Techniques50 835

[9]Granatstein V L,Parker R K,Armstrong C M 1999Proc.IEEE87 702

[10]Chu K R 2002IEEE Trans.Plasma Sci.30 903

[11]Calame J P,Garven M,Danly B G,Levush B,Nguyen K T 2002IEEE Trans.Electron Dev.49 1469

[12]Nusinovich G S 1999IEEE Trans.Plasma Sci.27 313

[13]Park G S,Choi J J,Park S Y,Armstrong C M,Ganguly A K 1995Phys.Rev.Lett.74 2399

[14]Sirigiri J R,Shapiro M A,Temkin R J 2003Phys.Rev.Lett.90 258

[15]Thottappan M,Singh S,Jain P K 2016IEEE Trans.Electron Dev.63 2118

[16]Denisov G G,Bratman V L,Phelps A,Samsonov S V 1998IEEE Trans.Plasma Sci.26 508

[17]Samsonov S V,Gachev I G,Denisov G G,Bogdashov A A,Mishakin S V,Fiks A S,Soluyanova E A,Tai E M,Dominyuk Y V,Levitan B A,Murzin V N 2014IEEE Trans.Electron Dev.61 4264

[18]Chu K R,Barnett L R,Chen H Y,Chen S H,Wang C 1995Phys.Rev.Lett.74 1103

[19]Chu K R,Chang T H,Barnett L R,Che S H 1999IEEE Trans.Plasma Sci.27 391

[20]Yan R,Tang Y,Luo Y 2014IEEE Trans.Electron Dev.61 2564

[21]Caplan M,Lin A T,Chu K R 1982Int.J.Electron.53 659

[22]Chu K R,Barnett L R,Lau W K,Chang L H,Lin A T,Lin C C 1991Phys.Fluids B:Plasma Phys3 2403

[23]Latham P E,Nusinovich G S 1995Phys.Plasmas2 3494

[24]Latham P E,Nusinovich G S 1995Phys.Plasmas2 3511

[25]Nusinovich G S,Walter M,Zhao J 1998Phys.Rev.E58 6594

[26]Peng S,Wang Q,Luo J,Zhang Z 2014Acta Phys.Sin.63 207401

[27]Tang Y,Luo J,Xue Q,Fan Y,Wang X,Peng S,Li S 2017IEEE Trans.Electron Dev.64 543

[28]Harrington R F 1961Time Harmonic Electromagnetic Fields(New York:McGraw-Hill)

[29]Pozar D M 1998Microwave Engineering(New York:Wiley)

[30]Tigelis I G,Vomvoridis J L,Tzima S 1998IEEE Trans.Plasma.Sci.26 922

[31]Tang Y,Luo Y,Xu Y,Yan R 2014J.Infr.Millim.THz Waves35 799

[32]Xue Q Z,Du C H,Liu P K,Zhang S C 2012Proc.IEEE IVEC421