100 keV质子与低高能质子在绝缘微孔中输运特性的对比分析∗
朱炳辉 杨爱香 牛书通 陈熙萌 周旺2) 邵剑雄
1)(兰州大学核科学与技术学院,兰州 730000)
2)(中核龙瑞科技有限公司,嘉峪关 735100)
1 引 言
随着纳米科技的发展,固体表面纳米结构研究取得了很大进展[1],这使得利用各种材料制作纳米尺度微孔成为可能.使用高能重离子辐照和化学刻蚀方法[2]可以制作出从微米到纳米尺度不同形状[3]和大小[4,5]的绝缘微孔膜,基于不同材料纳米微孔内部的电特性,越来越多的实验小组已参与到离子与微孔膜相互作用的研究中.
2002年,Stolterfoht小组[6−8]首次发现几keV低能高电荷态离子穿过内部充放电平衡的微孔后存在明显的导向效应.实验中,微孔轴向相对离子入射方向有几度的倾角,离子打在微孔表面有电荷沉积.当达到电荷平衡态后,入射离子靠近微孔表面时会在内壁发生小角度散射,而且几乎所有高电荷态离子都沿轴向出射并保持原有的电荷态.随后,Vienna小组[9−15]从理论方面详细研究了低能高电荷态离子的导向机制,其中的电荷斑扩散和漂移模型有助于理解微孔内壁沉积电荷斑自组织充放电过程.
之后,各小组研究发现MeV能量的离子通过锥形管微孔膜时[16−18],出射的粒子束存在明显的聚焦效应[19,20].除了在入射中心有亮斑外,进入固体内部的粒子发生随机碰撞,以小角度出射并在入射中心周围形成环形斑.但是,MeV离子通过锥形管时有关电荷交换和非弹性碰撞过程的模拟依然欠缺.Hasegawa等[21]利用粒子与靶原子核近距离碰撞的卢瑟福散射模型首次成功计算出传输粒子的轨迹和能量分布,其中的能量损失部分主要是由于粒子进入表面以下发生多次随机二体碰撞.
对于百keV中能离子在微孔膜中的传输,微孔内壁沉积电荷斑不再占绝对的主导作用,在表面原子层发生的多次小角度散射就比较重要.根据实验和理论模型计算[22,23],在百keV能量附近,微孔膜对高电荷态离子的导向效应不再明显.我们小组在实验研究100 keV质子传输特性时发现,粒子很可能是通过“电荷斑辅助的镜面反射”机制穿出微孔膜[24,25].从实验结果可以看出,出射粒子并非是完全的导向效应,初期粒子出射角分布在微孔轴向方向,达到平衡态后,粒子出射方向开始转向平行于入射束流方向.
目前,对于keV低能区,实验和理论研究都比较完备,普遍认为微孔膜对高电荷态入射离子具有“动态导向效应”.在MeV高能区,微孔内壁沉积电荷斑对入射离子穿过微孔膜没有影响,而进入表面以下多次非弹性碰撞是其主要的传输机制,这一点已经在实验和理论计算方面得到验证.对于几十至几百keV中间能区的入射离子,实验表明粒子通过微孔膜时不再是完全的导向效应.本文建立了能描述全能区(keV—MeV)带电粒子在微孔中传输的理论模型,重点讨论百keV能区质子的输运机制,并将模拟结果和实验进行对比,形成更加完整清晰的物理图像,以加深对中能区离子在微孔中传输特性的认识.
2 理论模型
带电粒子与微孔相互作用的模拟其实就是粒子在孔内的运动轨迹以及粒子与微孔内壁原子相互作用的模拟.考虑到不同能区粒子入射至微孔后将受到三种力的作用:沉积电荷斑产生的长程库仑力、表面原子层的集体散射力以及粒子进入表面以下与固体内部原子发生的一系列随机二体碰撞力.为清楚理解以上三种力哪种占主导作用,给出不同能区粒子以一定角度入射至微孔后,在距离微孔表面不同位置时发生偏转的轨迹示意图,如图1所示.

图1 质子在PC微孔中输运过程的轨迹示意图,其中R为微孔半径,Rexc为电荷交换距离Fig.1.Trajectory diagram of proton passing through the PC nanocapillary,where R presents the capillary radius and Rexcpresents the charge exchange distance.
低能区的粒子入射至微孔内主要受到表面电荷斑的库仑排斥力,此时表面电荷斑强,粒子在距离表面较远处就会发生偏转沿孔道方向出射;高能区的粒子进入微孔后由于横向动量较大,进入固体内部且碰撞中最接近距离远远小于原子晶格大小而发生多次二体碰撞;中能区粒子则由于横向动量大而有机会接近微孔内壁表面原子层,且碰撞中最接近距离在晶格大小量级,所以受到电荷斑的库仑排斥力和表面原子层的集体散射力的共同作用.以上几种力的不同特性使得不同能区粒子在微孔内的传输机制存在很大不同.下面详细探讨粒子在微孔中运动时受到的这三种力.
2.1 表面以上
带电粒子运动至微孔内表面以上一定距离时,会发生电子俘获,这个距离称为电荷交换距离Rexc.在该距离内入射粒子成为中性粒子,同时靶材料失去电子呈正电性.电荷交换距离的大小与入射粒子电荷、微孔材料有关.
通过参考质子打水和氢的俘获截面数据,得到100 keV质子碰撞水分子的俘获截面约为4.8×10−17cm2[26],100 keV质子碰撞氢分子的俘获截面为2.1×10−17cm2[27].聚碳酸酯(PC)材料的分子式为C16H14O3,则根据Bragg法则可以得到100 keV质子与PC材料作用的平均电子俘获截面σmean为2.0×10−17cm2,得到质子碰撞PC微孔的电荷交换距离Rexc为

粒子入射至微孔内,在接近微孔内壁到达Rexc时发生电子俘获,内壁表面失去一定量的电子,留下一个带同样正电荷的电荷斑.Lilly和McDowell[28]通过实验研究,发现沉积在绝缘材料上的点电荷不会消失,而是以体扩散的方式进行缓慢衰减,在∆t时间内衰减为[9,29]

式中,qi为第i个沉积电荷电荷量,ri为第i个沉积电荷的位置矢量,τd为微孔表面放电时间常数,由绝缘材料的离子电导性和深陷阱态决定.在模拟聚酯薄膜(PET)微孔膜中低能高电荷态离子导向效应时,Schiessl等[9]将PET膜放电时间设定为2—5 min,最终计算结果与实验数据能够吻合.考虑本文使用的PC膜导电性与PET膜类似[30],程序中将τd的值取为5 min是合理的.
进入微孔后的带电粒子,受到的微孔内壁沉积电荷势Uguid就是沉积在表面所有点电荷电势的叠加,即

式中,Q为入射粒子电荷,r为入射粒子的位置矢量.
2.2 近表面行为
当带电粒子接近微孔内表面原子的距离在数个原子单位时,会感受到表面原子层上数十至数百个原子散射力的共同作用.由于核外电子对原子核有屏蔽作用,因此模拟中采用Moliere屏蔽库仑势Uscat[31]描述内表面大量原子对入射粒子的集体散射势.

式中,Zp为入射粒子的核电荷数,Zt为靶原子的核电荷数,q为电子电荷,rsi为入射粒子与表面第i个原子之间的位矢,p是屏蔽长度,a0为玻尔半径.
由于Moliere势是相对近程的相互作用,依赖表面原子位置分布,为使模拟与实际情况接近,程序中采取原子在三维空间随机分布的方式使其处于原子平均间距δr附近.

式中,mC16H14O3为C16H14O3分子的质量,ρPC为PC材料密度,取1.20 g/cm3,33为一个C16H14O3分子中的原子个数.
当表面原子按晶阵式排列好后,给每个原子所在位置加上一个三维偏移量,

式中Ri为第i个表面原子的位矢;Rilattice为第i个表面原子按晶格排列取的位矢;ε表征原子位置随机化量的大小,为使表面原子不重合,需满足|ε|=0.5.
模拟中,表面原子分布按照PC材料中C,H,O的比例产生,已知PC膜分子式C16H14O3,得到三种原子所占的原子比分别为48.5%,42.4%,9.1%,通过蒙特卡罗方法抽样,可以确定每个位置的原子种类.
2.3 表面以下行为
当粒子入射至微孔内表面以下时,由于表面以下原子近似均匀分布在入射粒子周围,粒子感受到的往往是最接近的那个靶原子核的作用力,因此,随机二体碰撞是一个很好的近似.为了简化模型并降低运算时间,质子在材料内部的散射可以认为是质子与裸靶原子核相互排斥的作用,程序中考虑的物理过程是卢瑟福散射.碰撞的微分截面由卢瑟福散射公式求得:

式中,θs为质心系下粒子的散射角,Ek是入射粒子的动能.
通过对微分截面积分,得到总的散射截面σT:

理论上,积分限应该为0到π,为了避免微分截面在0点出现歧离,本次模拟中取θmin=1.0 mrad.
求得入射粒子在材料中的平均自由程为

式中,N为单位体积内所有原子的个数.
由于两次碰撞间的距离为l的概率服从指数分布[21],即

由此可以抽样得到两次碰撞之间的距离.
根据已知的微分散射截面,可以得到粒子在表面以下发生碰撞后散射到散射角从θmin到θs之间的概率P2(θs)[21]:

由于0<P2(θs)<1,故可用随机数ξ代替P2(θs),求得θs满足:

由此抽样得到粒子发生碰撞后的散射角度.
粒子入射至表面以下,最终可能从表面出射或者继续向表面以下运动.考虑到100 keV质子在PC材料中的射程大约为1.1µm,模拟中设定PC微孔内表面以下的深度为10µm,当运动距离超过射程则粒子停止.
入射粒子在与表面以下靶原子核碰撞过程中,有一定的概率失去电荷,即发生电荷损失,氢原子变成质子.通过玻尔公式计算得到固体内部粒子平衡电荷态Qmean:

对于100 keV质子,v=2.0 a.u,PC材料的平均核电荷数Zmean=3.729,则Qmean=0.56.即入射质子在表面以下运动时有约56%的仍是质子,44%变为氢原子.
此外,入射粒子与靶原子核发生碰撞,靶原子可能发生原子激发、俘获或电离,粒子速度减慢.通过分析理论模型给出的大量数据,发现大部分入射粒子留在固体内部,少数在经过两到三次随机碰撞就又一次从表面出射,因此,非弹性碰撞过程的能量损失基本忽略.
2.4 运动轨迹求解
本次模拟与实验参数保持一致[17],模型中PC微孔孔长lm=30µm,孔半径rm=100 nm,入射质子能量Ek=100 keV,束流密度ρ=1 nA/mm2,发散角θm=0.0847°.模拟时认为质子逐个入射至微孔内,则相邻两质子之间的时间间隔∆t为:

要得到粒子在微孔表面以上的运动轨迹,需要求解哈密顿方程.质子在微孔中运动的哈密顿量可以表示为

若质子接近内表面到达电荷交换距离Rexc,则质子俘获电子变为氢原子,氢原子在运动过程中的哈密顿量可以表示为

通过解哈密顿运动方程,可以得到
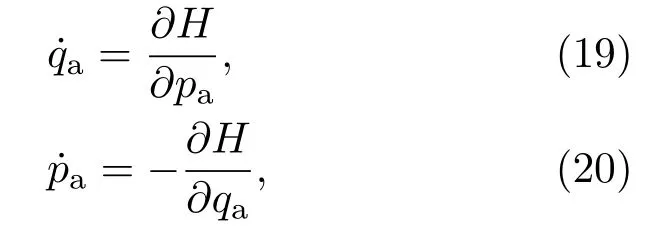
式中,qa为广义坐标,pa为广义动量.
若粒子进入微孔内表面以下,则通过蒙特卡罗随机抽样方法得到二体碰撞中的散射角和出射粒子电荷态,根据从表面出射的粒子电荷态选择对应的哈密顿方程求解随后粒子的运动轨迹,直至粒子从微孔穿出,在到达距离出口60µm处认为粒子不再受电荷斑影响,记录粒子的出射状态.
3 结果与讨论
图2给出了低中高能质子以−1°倾斜角入射PC微孔后,出射的H+在初期和末期的角分布谱图.模拟采用广义坐标,定义0°方向为微孔轴向方向(G),−1°方向为入射束流方向(B).对10 keV质子,在模拟初始阶段,出射角峰位在−0.3°附近,半高宽约为1.6°.随着入射质子数目增多,孔内壁电荷沉积达到动态平衡,出射H+的相对份额达到最大,峰位保持在0°附近,半高宽约为0.25°.对于1 MeV入射质子,在模拟初期和末期,出射H+的峰位没有发生明显变化,均在0.25°附近,且出射的H+数目相对较少,相对份额差异性较小.对于100 keV质子,出射的H+在初期和末期的角分布与10 keV和1 MeV存在明显差异,初期H+沿着微孔轴向附近出射,半高宽约为1.2°,当微孔内壁充放电达到平衡后,H+的相对份额达到最大,出射角开始转向入射束流方向,H+集中在−0.9°附近,半高宽约为0.65°.

图2 10 keV,100 keV,1 MeV质子以−1◦倾斜角入射PC微孔后出射H+的角分布Fig.2.The angular distribution of transmitted H+particles with proton incident energies of(a)10 keV,(b)100 keV and(c)1 MeV at−1◦title angle into the PC nanocapillary.
出射H+峰位角随入射质子数目的时间演化特性如图3所示,对于10 keV质子,在微孔内壁电荷斑建立过程中,出射H+峰位角沿着微孔轴向发生振荡.在入射质子数目达到30000个前,出射H+峰位位于−0.5°—0°,随着充放电的进行,当入射质子数目为30000—75000个时,出射H+峰位在0°—0.4°,之后达到平衡态,峰位处于−0.1°附近,说明此时绝大多数H+沿着微孔轴向出射.对1 MeV质子,在模拟的整个过程中,没有发现质子穿过微孔时明显的时间演化特性,出射的H+峰位角分布在0.33°—0.48°.对100 keV质子,在初期入射质子数目达到10000个前,出射H+的峰位角分布在−0.05°—−0.25°之间,表明此时H+沿着微孔轴向附近出射.随着充放电的进行,当入射70000个质子时,达到电荷平衡态,出射H+的峰位角开始向入射束流方向移动,并保持在−0.9°附近.
从图2和图3中可以看出,100 keV质子在微孔中的输运机制与10 keV和1 MeV存在明显的差异,为了直观描述这种差异性,图4给出了平衡状态下低中高能质子在微孔内壁表面电荷斑作用下的三维轨迹图,图中蓝色线表示质子传输轨迹,红色点表示微孔内壁表面沉积电荷.
由于受微孔尺寸的影响(纵横比为150:1),10 keV质子入射微孔后不能直接从孔道穿出,而在与微孔表面碰撞过程中留下电荷.随后入射的质子在第二块电荷斑的库仑排斥力下发生偏转沿微孔轴的一侧出射,部分受到出口处第三块电荷斑的作用力沿着微孔另一侧出射.当充放电平衡后,入射质子在内部电荷斑共同辅助下沿着微孔轴向出射,这与低能高电荷态离子出射中心角在平均角附近出现振荡的效应类似[8],可以解释图3(a)中出射H+峰位角沿着微孔轴向振荡最终达到平衡的时间演化特性.
对于1 MeV质子,由于横向动量较大,微孔表面沉积电荷斑对质子的传输不再起主导作用,使得模拟过程中没有发现出射H+角分布明显的时间演化特性,如图3(c)所示.质子入射至微孔内,与表面以下原子发生多次随机二体碰撞,绝大多数留在固体内部,少量粒子从微孔表面出射,从而解释了图2中1 MeV能量质子入射微孔后出射数目相对较少的原因.从表面出射的H+失去原有轨迹信息,沿出口方向发生随机散射,轨迹变得曲折且很不规则.

图3 10 keV,100 keV,1 MeV质子以−1◦倾斜角入射PC微孔后出射H+的峰位角演化Fig.3.The evolution of centroid angle of transmitted H+particles with proton incident energies of(a)10 keV,(b)100 keV and(c)1 MeV at−1◦title angle into the PC nanocapillary.

图4 平衡状态下10 keV,100 keV,1 MeV质子以−1◦倾斜角入射PC微孔后出射H+的三维轨迹图Fig.4.Three-dimensional trajectories of H+particles passing through the PC nanocapillary with proton incident energies of(a)10 keV,(b)100 keV and(c)1 MeV at−1◦title angle after equilibrium.
对于100 keV质子,如图4(b)所示,由于横向动量大,在质子入射的初始阶段,微孔内壁只有少量的电荷沉积,粒子进入表面以下发生二体碰撞产生随机散射,使得出射质子失去原有的轨迹信息,在微孔中的轨迹变得曲折,最终沿着微孔轴向附近出射.随着电荷进一步沉积,越来越多的入射质子被电荷斑托起,不能进入表面以下,但电荷斑不足以完全克服100 keV质子的横向动量.绝大多数质子可以到达表面附近,此时表面原子层集体散射力起到关键作用,使得表面附近质子以镜面反射方式偏转到另一侧,形成第二块电荷斑.当达到充放电平衡后,入射质子在第一和第二块电荷斑处发生两次镜面散射,最终沿入射束流方向出射,这一点符合图3(b)中出射H+峰位角的时间演化特性.
以上结果表明,对于10 keV低能质子入射微孔,内壁表面沉积电荷斑的导向力占主导作用,这与低能高电荷态离子的导向机制类似[8].对于1 MeV高能质子,粒子进入表面以下发生的二体碰撞随机散射决定粒子出射状态,可以从MeV质子与玻璃锥形管相互作用的实验和理论研究[21]中得到印证.而对于100 keV中能质子,当孔内电荷充放电平衡后,入射质子是在电荷斑导向力辅助作用下,经由表面原子层的集体散射力,发生近表面的镜面散射行为,这一点区别于低能和高能质子的输运机制.
为了进一步研究中能质子的传输特性,下面给出100 keV质子在微孔中传输时碰撞次数、出射H+的相对穿透率以及电荷纯度随时间演化的特性.
图5统计模拟了初期和末期10000个质子入射至微孔内,进入表面以下以及在表面以上发生散射的粒子数,图中横坐标表示粒子与靶原子核发生二体碰撞或在表面以上发生散射的次数,纵坐标对应发生该事件的粒子数.从图5(a)可以看出,在模拟初始阶段,大约有89.2%的入射粒子进入表面以下与靶原子核发生随机二体碰撞,此时微孔内壁表面电荷斑较弱,大部分粒子能够克服电荷斑库仑排斥力进入表面以下,这也就是初期进入表面以下粒子数所占比重很大的原因.到模拟后期,进入表面以下的粒子数占到71.4%,这是因为微孔表面建立的电荷斑能在一定程度上抑制粒子进入表面以下.粒子入射至表面以下,最终可能从表面出射或留在表面以下.从图5(b)可以看出,在模拟的初始阶段有41.9%左右的粒子在微孔表面以上发生散射,当到达平衡后,内表面处散射次数增加到63.4%,这是由于在微孔另一侧建立的电荷斑增加粒子在表面原子层发生镜面散射的次数.

图5 100 keV质子以−1◦倾斜角入射PC微孔后初末状态进入表面以下粒子数以及在表面以上发生散射的粒子数统计Fig.5.Statistics of the number of particles(a)entering into surface and(b)scattering above the surface at the beginning and after equilibrium with proton incident energy of 100 keV at−1◦tilt angle into the PC nanocapillary.

图6 100 keV质子以−1◦倾斜角入射PC微孔后出射H+相对穿透率以及H+占总出射粒子的相对份额(电荷纯度)演化过程Fig.6.The evolution of the relative transmission rate and relative proportion of protons(charge purity)of H+particles with proton incident energy of 100 keV at−1◦title angle into the PC nanocapillary.
图6所示为模拟过程中出射H+的相对穿透率以及电荷纯度随入射质子数的时间演化特性.从图中可以看出,当入射质子数目为30000个时,出射H+的相对穿透率以及电荷纯度明显上升,说明这段时间电荷斑的建立对质子出射微孔具有增强作用.当入射质子数目达到80000个时,随着微孔内壁充电过程的进行,质子开始偏转到微孔另一侧形成第二块电荷斑,这个过程中H+的相对穿透率以及电荷纯度只有缓慢的增加.当入射质子数目达到80000以后,第二块电荷斑已建立,微孔内部充放电达到平衡,在电荷斑的库仑排斥力下,绝大部分质子不能进入电荷交换距离Rexc,在到达近表面处发生镜面反射,最终使得H+的相对穿透率基本保持不变,电荷纯度在66%—72%之间波动.简而言之,对于100 keV入射质子,微孔内壁两侧沉积电荷斑对质子保持原有电荷态并沿入射方向出射具有明显的增强作用.
从以上结果中可以看出,100 keV质子以−1°倾斜角入射穿过微孔时不再是完全的导向效应,当达到平衡后,表面原子层的集体散射力起到关键作用,使得到达表面附近的质子按镜面反射方式出射.具体表现为:由于质子横向动量大,在模拟初始阶段,微孔内壁电荷斑较弱,绝大部分粒子克服库仑排斥力作用直接进入表面以下发生随机二体碰撞,失去了原有轨迹信息,出射的粒子沿着微孔轴向出射.随着微孔内壁电荷累积,增强的库仑排斥力明显地抑制了质子在微孔内表面电子俘获过程.达到充放电平衡后,质子在电荷斑辅助的镜面反射机制下沿入射方向出射,出射粒子的相对穿透率和电荷纯度较模拟初期有显著提升.
为了验证模拟结果,图7给出了100 keV质子以−1°倾斜角入射微孔后出射H+角分布与实验数据的对比结果,图中纵坐标采用归一化处理,给出相对强度值进行比较.从图中可以看出,该模拟方法可以对能量为100 keV中能区质子通过微孔后的角分布进行很好的描述,主要体现为,在到达平衡态后质子的出射方位分布在−1°附近,即入射束流方向,同时也能较好地重现0°附近出现的较平缓肩部.

图7 平衡状态下100 keV质子以−1◦倾斜角入射PC微孔后出射H+的角分布实验值与模拟值对比,其中蓝色柱状图为模拟结果,红色实线为实验结果Fig.7.Measured data(red solid line)and simulation results(blue bar)of the angular distribution spectrum of the transmitted H+particles after equilibrium with proton incident energy of 100 keV at−1◦ title angle into the PC nanocapillary.
4 结 论
为了对中能区质子在微孔中输运的物理图像有更加完整清晰的认识,本文建立了带电粒子在微孔中传输的理论模型,得到10 keV,100 keV和1 MeV质子以−1°倾斜角入射微孔后出射H+的角分布、沉积电荷斑分布以及粒子在微孔中运动轨迹等传输特性,发现百keV质子在微孔中的输运机制与低能和高能存在明显不同.通过与实验结果进一步对比分析,发现100 keV质子从微孔出射不再是完全的导向效应.无电荷沉积时,表面以下多次随机非弹性散射过程是主要的输运机制,到达充放电平衡态后,入射质子在表面电荷斑辅助下发生近表面的镜面散射行为,经两次反射后沿着平行于入射束流方向出射,这一效应将有助于对该能区微束的控制和应用.
[1]El-Said A S,Heller R,Meissl W,Ritter R,Facsko S,Lemell C,Solleder B,Gebeshuber I C,Betz G,Toulemonde M,Möller W,Burgdörfer J,Aumayr F 2008Phys.Rev.Lett.100 237601
[2]Mo D,Liu J,Duan J L,Yao H J,Chen Y H,Sun Y M,Zhai P F 2012Mater.Lett.68 201
[3]Kottmann J P,Martin O J F,Smith D R,Schultz S 2001Phys.Rev.B64 235402
[4]Máté fi-Temp fl i S,Máté fi-Temp fl i M,Piraux L,Juhász Z,Biri S,Fekete É,Iván I,Gáll F,Sulik B,Víkor G,Pálinkás J,Stolterfoht N 2006Nanotechnology17 3915
[5]Rajendra-Kumar R T,Badel X,Vikor G,Linnros J,Schuch R 2005Nanotechnology16 1697
[6]Stolterfoht N,Bremer J H,Hoffmann V,Hellhammer R,Fink D,Petrov A,Sulik B 2002Phys.Rev.Lett.88 133201
[7]Juhász Z,Sulik B,Rácz R,Biri S,Bereczky J R,Tökési K,Kövér Á,Pálinkás J,Stolterfoht N 2010Phys.Rev.A82 062903
[8]Stolterfoht N 2013Phys.Rev.A87 032901
[9]Schiessl K,Pal fi nger W,Lemell C,Burgdörfer J 2005Nucl.Instrum.Methods Phys.Res.B232 228
[10]Schiessl K,Pal fi nger W,Tőkési K,Nowotny H,Lemell C,Burgdörfer J 2005Phys.Rev.A72 062902
[11]Schiessl K,Pal fi nger W,Tőkési K,Nowotny H,Lemell C,Burgdörfer J 2007Nucl.Instrum.Methods Phys.Res.B258 150
[12]Lemell C,Schiessl K,Nowotny H,Burgdörfer J 2007Nucl.Instrum.Methods Phys.Res.B256 66
[13]Schiessl K,Lemell C,Tökési K,Burgdörfer J 2009J.Phys.Conf.Ser.163 012081
[14]Schiessl K,Lemell C,Tökési K,Burgdörfer J 2009J.Phys.Conf.Ser.194 012069
[15]Schweigler T,Lemell C,Burgdörfer J 2011Nucl.Instrum.Methods Phys.Res.B269 1253
[16]Nebiki T,Yamamot T,Narusawa T,Breese M B H,Teo E J,Watt F,Vac J 2003Sci.Tech.A:Vacuum,Surfaces,and Films21 1671
[17]Nebiki T,Sekiba D,Yonemura H,Wilde M,Ogura S,Yamashita H,Matsumoto M,Fukutani K,Okano T,Kasagi J,Iwamura Y,Itoh T,Kuribayashi S,Matsuzaki H,Narusawa T 2008Nucl.Instrum.Methods Phys.Res.B266 1324
[18]Sekiba D,Yonemura H,Nebiki T,Wilde M,Ogura S,Yamashita H,Matsumoto M,Kasagi J,Iwamura Y,Itoh T,Matsuzaki H,Narusawa T,Fukutani K 2008Nucl.Instrum.Methods Phys.Res.B266 4027
[19]Hasegawa J,Jaiyen S,Polee C,Chankow N,Oguri Y 2011J.Appl.Phys.110 044913
[20]Simon M J,Zhou C L,Döbeli M,Cassimi A,Monnet I,Méry A,Grygiel C,Guillous S,Madi T,Benyagoub A,Lebius H,Müller A M,Shiromaru H,Synal H A 2014Nucl.Instrum.Methods Phys.Res.B330 11
[21]Hasegawa J,Jaiyen S,Polee C,Chankow N,Oguri Y 2011J.Appl.Phys.110 044913
[22]Wu Y H,Yu D Y,Xue Y L,Chen J,Liu J L,Zhang M W,Wang W,Lu R C,Ruan F F,Du F,Shao C J,Li J Y,Kang L,Cai X H 2014Nucl.Instrum.Methods Phys.Res.B334 59
[23]Xue Y L,Yu D Y,Liu J L,Wu Y H,Zhang M W,Chen J,Wang W,Lu R C,Shao C J,Kang L,Li J Y,Cai X H,Stolterfoht N 2015Nucl.Instrum.Methods Phys.Res.B359 44
[24]Wang G Y,Shao J X,Song Q,Mo D,Yang A X,Ma X,Zhou W,Cui Y,Li Y,Liu Z L,Chen X M 2015Sci.Rep.5 15169
[25]Zhou W,Niu S T,Yan X W,Bai X F,Han C Z,Zhang M X,Zhou L H,Yang A X,Pan P,Shao J X,Chen X M 2016Acta Phys.Sin.65 103401(in Chinese)[周旺,牛书通,闫学文,白雄飞,韩承志,张鹛枭,周利华,杨爱香,潘鹏,邵剑雄,陈熙萌2016物理学报65 103401]
[26]Errea L F,Illescas C,Méndez L,Pons B,Rabadán I,Riera A 2007Phys.Rev.A76 040701
[27]Illescas C,Riera A 1999Phys.Rev.A60 4546
[28]Lilly Jr A C,McDowell J R 1968J.Appl.Phys.39 141
[29]Stolterfoht N,Bremer J H,Hoffmann V,Hellhammer R,Fink D,Petrov A,Sulik B 2002Phys.Rev.Lett.88 133201
[30]Stolterfoht N,Hellhammer R,Sulik B,Juhász Z,Bayer V,Trautmann C,Bodewits E,Hoekstra R 2011Phys.Rev.A83 062901
[31]Yang F J 2008Atom.Phys.(Beijing:Higher Education Press)p95(in Chinese)[杨福家 2008原子物理学(北京:高等教育出版社)第95页]

