漫反射立方腔单次反射平均光程的理论和实验研究∗

张云刚 刘如慧 汪梅婷 王允轩 李占勋 童凯

(燕山大学电气工程学院,秦皇岛 066004)

1 引 言

气体浓度监测被广泛应用于环境保护、食品安全和医学救助等领域.对SO2,NO,CO2等污染气体的监测,可实现对工业生产过程中排放污染物的监测[1−3];微生物新陈代谢会产生CO2,因此可通过检测CO2的浓度对食品是否变质进行判定[4];通过对人体呼出微量气体的检测来实现对心肺功能以及其他疾病的诊断[5,6].吸收光谱法因其具有高选择性、抗干扰、高灵敏、非接触性以及可实时在线监测等优点,成为气体监测领域的主要监测方法.使用吸收光谱法检测气体浓度时,为了实现低浓度气体的测量,需提高检测系统的灵敏度.增加气体有效光程作为提高气体探测灵敏度最直接有效的方法,得到了广泛的关注和研究.常用的增加气体有效光程的方法有多通池、腔增强、多孔散射和积分球.其中,多通池和腔增强技术是通过增加光在样品池内的镜面反射次数来增加有效光程的[7,8].多孔散射法由瑞典隆德大学Svanberg的研究小组[9]于2001年首次提出,是一种检测多孔散射材料中气体浓度的方法,光进入散射材料后发生散射,实现了有效光程的增加.积分球是内表面涂有高漫反射材料的球体,通过光在积分球内的漫反射实现有效光程的增加.1996年,Tranchart等[10]首次将积分球作为气体吸收池,用于可调谐二极管激光吸收光谱(tunable diode laser absorption spectroscopy,TDLAS)技术测量气体浓度的实验中,并实现了丁烷和水蒸气浓度的测量.将积分球作为气体吸收池进行气体浓度测量,可以有效地避免镜面反射易产生干涉条纹以及多孔散射材料噪声大的缺点[11−13],但是积分球也存在着制作困难、价格昂贵、难于集成的问题.为了进一步拓展漫反射腔在高灵敏气体检测中的应用,在积分球的基础上开展了漫反射立方腔的研究,通过实验研究发现漫反射立方腔不仅具有积分球的优点,而且制作简单、价格低廉、易于集成.

TDLAS是由Hinkley和Reid于20世纪80年代提出的,通过对具有很窄发射波段的二极管激光器的调谐,使其扫描过一个完整的待测气体的吸收谱线,根据采集到的吸收光谱来确定待测气体浓度[14,15].TDLAS技术具有很高的选择性,只要选择合适的吸收线即可有效地避免其他气体的干扰[16−18].近年来,将漫反射立方腔作为气体吸收池进行气体浓度检测已有大量的理论和实验研究,尤其是对漫反射立方腔的光程延长规律和气体有效光程的研究方面[19].本文在增加有效光程实验研究的基础上开展了漫反射立方腔内的光线传播规律的研究,利用有限元法对立方腔进行分割,仿真得到了单次反射平均光程(single re fl ection average optical path length,Lave)的模拟值.将得到的模拟值与理论值和实验值进行了比较,发现三者具有很高的符合度,证明有限元法能够实现对漫反射立方腔内光线传播规律的模拟.

2 漫反射立方腔单次反射平均光程的理论和模拟研究

基于腔内光子传输方程,可得任意形状的漫反射腔的单次反射平均光程[20,21]

其中,V为任意漫反射腔的体积,S为任意漫反射腔的表面积.

对于漫反射立方腔,其内部形成的是均匀且稳定的光场[22].假设漫反射立方腔内壁的反射率接近于1,可以采用有限元法对腔内的光线传播规律进行模拟,以获得单次反射平均光程的模拟值.将立方腔内表面分割为众多小面元,令每个面元代表一个反射点.两个反射点之间的光程可以用空间坐标中两个反射点之间的线段长度来表示,则单次反射平均光程的模拟值Lave为

其中,Y为任一反射点与其他所有反射点之间线段的总长度,X为线段总个数.

令立方腔的边长为a,首先将立方腔的每个面分割成N×N个小面元,以立方腔底面ABCD的中心点O为坐标原点建立空间坐标系,如图1所示.令点O为光射入立方腔后第一次发生漫反射的反射点,经点O反射到立方腔各个面上的概率并不同,通过求解点O与各个面之间的立体角来表示其概率.设点O反射到面EFGH的内切圆O′的概率为α,如图2所示,反射到面EFGH的概率为β,则反射到面EFGH除去其内切圆O′部分的概率为β−α.可知反射到面ABCD的概率为1/2,所以反射到4个侧面的概率和为1/2−β.假设P为底面ABCD上任意一点,M为顶面DEGH上任意一点,N为侧面BCFG上任意一点.令点O与内切圆O′内所有反射点之间的线段总长度为x0,线段OM的总和为x,线段ON的总和为y,线段OP的总和为y0,可得立方腔单次反射平均光程的模拟结果为

其中,α和β分别满足

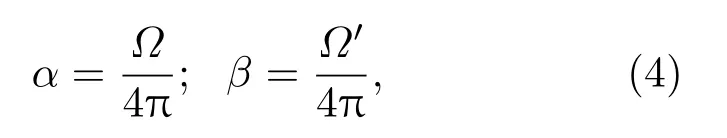
式中,Ω为点O到圆O′的立体角,Ω′为点O到面EFGH的立体角.由上述分析可得α=0.0528,β=0.0641.

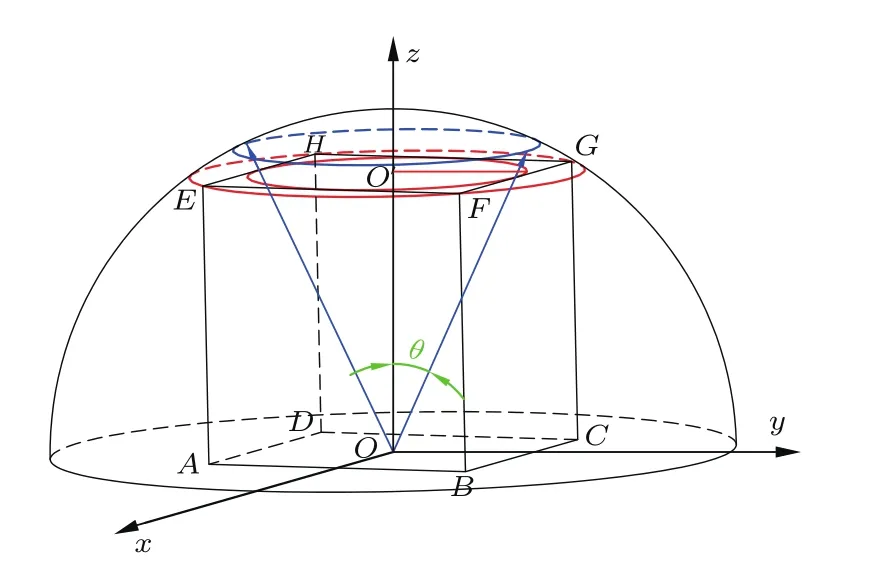
图1 漫反射立方腔理论模型示意图Fig.1.Theoretical model of the diffuse cubic cavity.

图2 顶面EFGH的内切圆O′Fig.2.Inscribed circle of top surface EFGH.

以边长为6 cm的立方腔为例,(3)式中N由1变化到2000,仿真可得不同N值时单次反射平均光程的模拟值,如图3(a)所示.根据(1)式可知,边长为6 cm的立方腔单次反射平均光程的理论值为4 cm.根据不同N值时的模拟值和理论值,可求得两者之间的相对误差值,如图3(b)所示.由图3可知,随着N值的增大,单次反射平均光程的模拟结果无限趋近于理论值4.13 cm.当N≥100时,模拟值逐渐趋于稳定,当N≥1000时,模拟值和理论值之间的相对误差变化微小,稳定在3.3%左右,在误差允许的范围内.说明利用有限元法对立方腔进行模拟,所得单次反射平均光程模拟值与理论值符合得很好,具有很好的模拟效果.

令N=1000,立方腔边长变化范围为1—12 cm,边长变化间隔为1 cm,可得不同边长立方腔对应的单次反射平均光程模拟值,同样求得模拟值与理论值之间的相对误差,如图4所示.

图3 边长为6 cm的立方腔单次反射平均光程 (a)模拟值;(b)模拟值与理论值的相对误差值Fig.3.(a)The simulation value,(b)the relative error with the theoretical value of the Laveof the cubic cavity with a side length of 6 cm.

由图4(a)可知,不同边长的立方腔与其对应的单次反射平均光程的理论值和模拟值之间的连线均呈线性关系,而且两条直线的偏差很小.从图4(b)可以看出,随着边长的增大,相对误差值逐渐趋于稳定,在3.53%上下存在微小波动.立方腔的边长从1 cm变化到12 cm,其单次反射平均光程的模拟值和相应的理论值符合得都很好,两者的相对误差在3.53%处趋于稳定,说明有限元法对不同边长的立方腔都具有很好的模拟效果.对不同边长立方腔单次反射平均光程的模拟值进行线性拟合,拟合直线的方程为

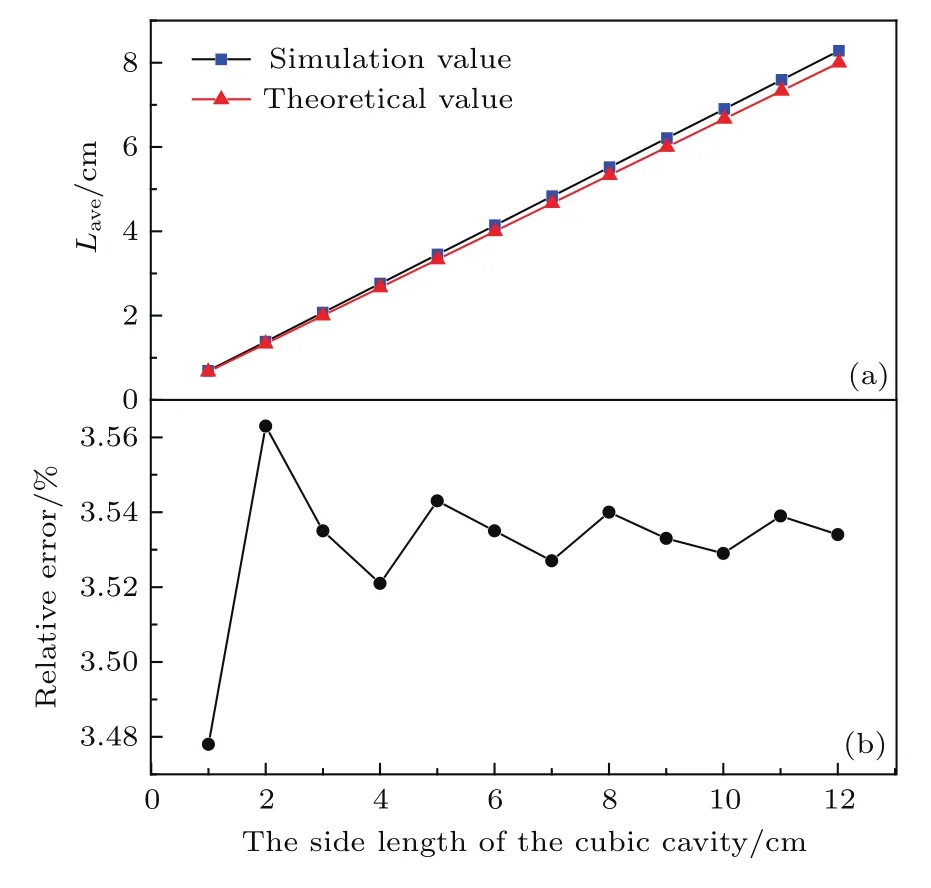
图4 不同边长立方腔单次反射平均光程 (a)模拟值和理论值;(b)相对误差值Fig.4.(a)The simulation values and the theoretical values,(b)their relative error of the Laveof the cubic cavities with different side length.

已知立方腔单次反射平均光程的理论公式为Lave=2/3a=0.67a,由此可知对模拟值拟合所得的直线与理论公式所对应的直线符合得很好,再次证明了有限元法对漫反射立方腔内光线传播规律具有很好的模拟效果.

3 漫反射立方腔有效光程的实验研究

3.1 Beer-Lambert定律

光谱法测量气体浓度的理论基础为Beer-Lambert定律,它描述了一束光经过一定长度的待测气体后出射光强与入射光强之间的关系,表达式为

式中I0(λ)为波长为λ的入射光强,I(λ)为经过气体吸收后的出射光强,ε为吸收截面,C为气体浓度,L为光与气体作用的长度,即有效光程(effective optical path length,Leff).由(6)式可得

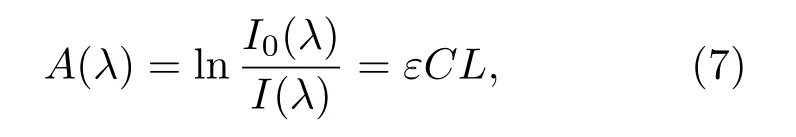
式中A(λ)为吸光度.定义光学参量(optical parameter,OP)为吸收波段内吸光度的求和,表示为

3.2 空气中氧气的定标实验

为了验证有限元模拟方法的准确性,进行了基于TDLAS的氧气定标实验,分析了模拟值和实验值的符合程度.由于氧气的吸收峰在760 nm附近,所以选择波长为760 nm的VCSEL二极管激光器(laser components,single mode VCSEL 760 nm TO46)作为光源.二极管激光器的温度和电流分别由温度控制器(Thorlabs,ITC 510)和电流控制器(Thorlabs,LDC 200)控制,电流控制器的输出范围为0—20 mA,精度为1µA,温度控制器的控温精度为0.001°C.在电流控制器上加载一个频率为20 Hz.振幅为200 mV的锯齿波,对激光二极管的波长进行调谐,使其可以扫描完整的氧气吸收峰.图5所示为定标的实验装置示意图.

图5 TDLAS实验装置示意图Fig.5.Schematic diagram of experimental set-up for TDLAS.

图6(a)所示为有效吸收光程为120 cm时氧气的二次谐波信号;图6(b)为不同吸收光程下的二次谐波信号.由图6(b)可知,随着吸收光程的增加,二次谐波信号的强度也随之增大.根据(8)式可知,气体浓度固定的条件下,气体的有效光程Leff与光学参量OP之间存在线性关系.

通过求和法求得不同有效光程下对应的OP值,对Leff和对应的OP值进行线性拟合,如图7所示,得到了有效光程Leff与光学参量OP的关系式为:

图6 (a)有效光程为120 cm的二次谐波信号;(b)不同有效光程下的二次谐波信号Fig.6.(a)Second harmonic signal at Leffof 120 cm;(b)second harmonic signals at different Leff.

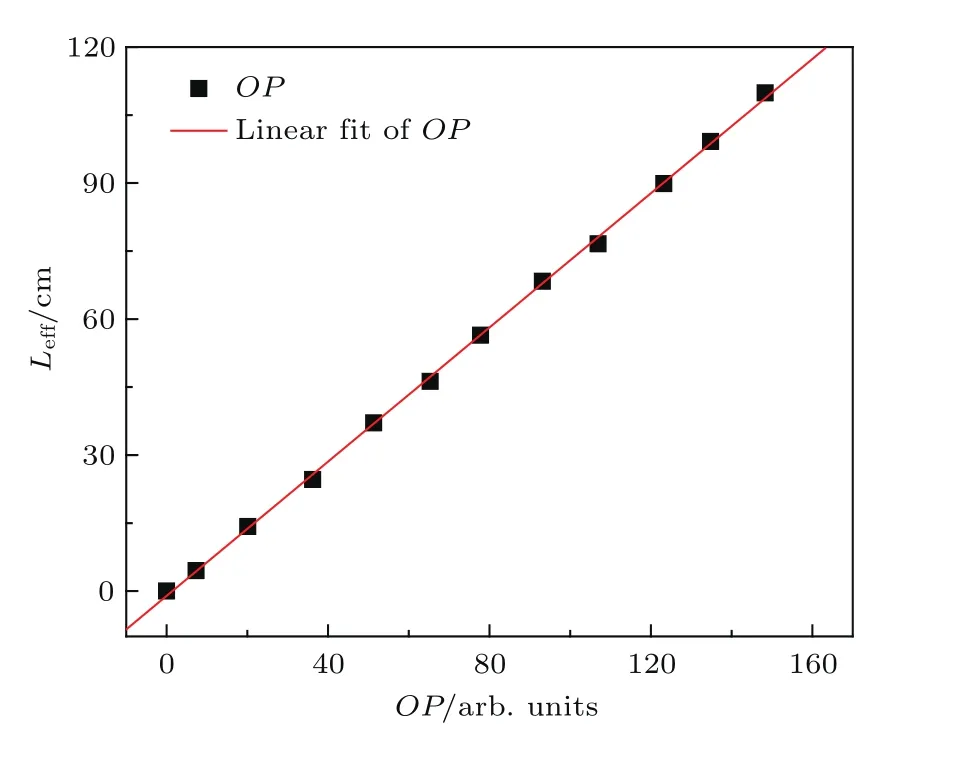
图7 光学参量和有效光程的关系Fig.7.The relationship between OP and Leff.

3.3 漫反射立方腔有效吸收光程的测量

对于漫反射立方腔,直接测量其单次反射平均光程极其困难,根据TDLAS实验研究,单次反射平均光程Lave与有效光程Leff的关系为[23,24]

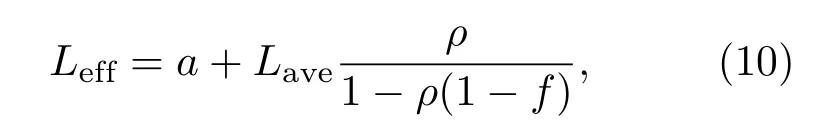
其中,ρ为漫反射涂层的反射率,f为立方腔的开孔比.若已知立方腔的有效光程,根据(10)式可得到其单次反射平均光程.

图8(a)所示为漫反射立方腔测量氧气浓度的TDLAS实验装置示意图,图8(b)为实物图,与定标实验不同的是高漫反射立方腔为气体吸收池.光线进入立方腔内,在其内表面发生漫反射,增加了有效光程,同时出射光强也变得很微弱,因此实验系统采用光电倍增管(Zolix,PMTH-S1-CR131)作为探测装置.分别对边长为5,8,12 cm的3种立方腔进行了实验研究.对边长为12 cm的立方腔而言,光学参量OP为121.15,代入(9)式可得有效光程Leff为162.43 cm.入射孔和出射孔均为直径为2 mm的圆孔,板子连接处共有12个缝隙,每个缝隙大约宽0.03 cm,开孔比f为0.0051,漫反射率ρ为95%.根据(10)式可得,边长为12 cm的漫反射立方腔的单次反射平均光程为8.71 cm.为了对比分析单次反射平均光程的理论值、模拟值和实验值之间的关系,分别求出理论值和模拟值之间的误差Q1,模拟值与实验值之间的误差Q2,以及理论值与实验值之间的误差Q3,如图9(b)所示.

图8 漫反射立方腔测量氧气浓度的TDLAS实验装置 (a)示意图;(b)实物图Fig.8.(a)Schematic diagram;(b)photograph of the set-up of experimental set-up for oxygen measurement with a diffuse cubic cavity based on TDLAS.

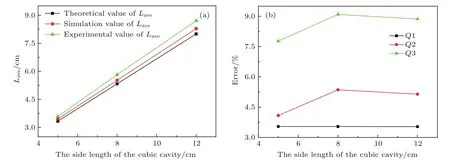
图9 边长为5,8,12 cm的立方腔单次反射平均光程理论值、模拟值和实验值之间的(a)对比图,(b)误差图Fig.9.(a)Comparison and(b)error between the theoretical value,the simulation value and the experimental value of the Laveof the cubic cavities with side length of 5 cm,8 cm and 12 cm.

由9(a)可以看出,无论是理论值、模拟值或实验值,单次反射平均光程与立方腔边长之间呈线性关系.而且模拟值所对应的连线位于理论值和实验值所对应的连线的中间,与两者的偏差都很小,说明模拟值与理论值和实验值符合得都很好,因此,可用模拟值替代实验值进行相关气体腔特性分析.根据图9(b)可知,对于不同边长的立方腔而言,模拟值与理论值之间的误差Q1最小,其次为模拟值与实验值之间的误差Q2,最大的为实验值与理论值之间的误差Q3,均在误差允许范围内,说明模拟值与理论值和实验值符合得都很好.有限元法对漫反射立方腔内光线传播规律的模拟达到了很好的效果,不仅为实验方法研究漫反射立方腔提供了一种理论支持,有助于公式的反演,而且可以为研究其他形状腔体的光线传播规律提供一种研究思路和方法,对漫反射腔的研究具有一定的参考价值.

4 结 论

基于对漫反射立方腔内光线传播规律的分析,利用有限元法仿真了漫反射立方腔内的光线传播,建立了单次反射平均光程与反射次数之间的关系.仿真结果表明,当把立方腔内每个表面分成1000×1000个以上的小面元时,仿真得到的单次反射平均光程与理论计算的单次反射平均光程的误差小于3.6%.对多种不同边长的立方腔进行模拟,发现不同边长立方腔的模拟值与相应理论值误差波动小于0.1%,说明有限元法对不同边长的立方腔都具有很好的模拟效果.通过TDLAS技术对3种不同边长的漫反射立方腔内的氧气吸收谱进行采集,分别获得了其对应的有效光程,并利用有效光程计算得到了单次反射平均光程的实验值.对比了理论、仿真和实验获得的单次反射平均光程,三者具有很好的一致性,表明对漫反射立方腔内光线传播规律的仿真研究对实验研究具有重要的参考价值,为以后开展任意形状漫反射腔吸收光谱技术的研究提供了一种技术支撑.

[1]Tang G H,Xu C L,Shao L T,Wang S M 2008Chin.J.Sci.Instru.29 244(in Chinese)[汤光华,许传龙,邵礼堂,王式民2008仪器仪表学报29 244]

[2]Yu M J,Liu M H,Dong Z R,Sun Y G,Cai H W,Wei F 2015Chin.J.Laser42 351(in Chinese)[郁敏捷,刘铭晖,董作人,孙延光,蔡海文,魏芳2015中国激光42 351]

[3]Liu J,Si F Q,Zhou H J,Zhao M J,Dou K,Wang Y,Liu W Q 2015Chin.Opt.Lett.35 337(in Chinese)[刘进,司福祺,周海金,赵敏杰,窦科,王煜,刘文清2015光学学报35 337]

[4]Liang H Z,Zhang X,Rao J,Chen H W 2008Chin.J.Biotechnol.28 124(in Chinese)[梁华正,张燮,饶军,陈焕文2008中国生物工程杂志28 124]

[5]D’Amico A,Pennazza G,Santonico M,Martinelli E,Roscioni C,Galluccio G,Paolesse R,Natale C D 2010Lung Cancer68 170

[6]Teh S K,Zheng W,Ho K Y,Teh M,Yeoh K G,Huang Z W 2010Int.J.Cancer126 1920

[7]Yang X B,Zhao W X,Tao L,Gao X M,Zhang W J 2010Acta Phys.Sin.59 5154(in Chinese)[杨西斌, 赵卫雄,陶玲,高晓明,张为俊2010物理学报59 5154]

[8]Hu R Z,Wang D,Xie P H,Ling L Y,Qin M,Li C X,Liu J G 2014Acta Phys.Sin.63 110707(in Chinese)[胡仁志,王丹,谢品华,凌六一,秦敏,李传新,刘建国 2014物理学报63 110707]

[9]Sjoholm M,Somesfalean G,Alnis J,Andersson-Engels S,Svanberg S 2011Opt.Lett.26 16

[10]Tranchart S,Bachir I H,Destombes J L 1996Appl.Opt.35 7070

[11]Lucke R L 2007Appl.Opt.46 6966

[12]Hwang J,Shin D J,Jeong K R 2016Metrologia53 1231[13]Fukutomi D,Ishii K,Awazu K 2015Lasers Med.Sci.30 1335

[14]Lackner M 2007Rev.Chem.Eng.23 65

[15]Wang F,Cen K F,Li N,Jeffries J B,Huang Q X,Yan J H,Chi Y 2010Meas.Sci.Technol.21 45301

[16]Gao Y W,Zhang Y J,Chen D,He Y,You K,Chen C,Liu W Q 2016Chin.Opt.Lett.36 275(in Chinese)[高彦伟,张玉钧,陈东,何莹,尤坤,陈晨,刘文清2016光学学报36 275]

[17]Zhou X,Yu J,Wang L,Gao Q,Zhang Z G 2017Sens.Actuators B:Chem.241 1076

[18]Gao G Z,Cai T D,Hu B,Jia T J 2015Spectrosc.Spect.Anal.35 34(in Chinese)[高光珍,蔡廷栋,胡波,贾天俊2015光谱学与光谱分析35 34]

[19]Yu J,Zheng F,Gao Q,Li Y J,Zhang Y G,Zhang Z G,Wu S H 2014Appl.Phys.B116 135

[20]Fry E S,Musser J,Kattawar G W,Zhai P W 2006Appl.Opt.45 9053

[21]Manojlovic L M,Marincic A S 2011Meas.Sci.Technol.22 075303

[22]Yu J 2014Ph.D.Dissertation(Harbin:Harbin Institute of Technology)(in Chinese)[虞佳 2014博士学位论文(哈尔滨:哈尔滨工业大学)]

[23]Yu J,Zhang Y G,Gao Q,Hu G,Zhang Z G,Wu S H 2014Opt.Lett.39 1941

[24]Yu J,Gao Q,Zhang Y G,Zhang Z G,Wu S H 2014J.Opt.16 125708