水下超声速气体射流诱导尾空泡实验研究∗

许昊 王聪 陆宏志 黄文虎

1)(哈尔滨工业大学航天学院,哈尔滨 150001)

2)(中国运载火箭技术研究院研究发展中心,北京 100076)

1 引 言

液体中的高速气体射流问题广泛存在于冶金、化工、水下推进等工程技术领域.相比较单相流体射流,这一问题包含气液两相速度及密度比大(通常在102量级以上),气液界面存在Kelvin-Helmholtz(K-H)、Reyleigh-Taylor和Richtmyer-Meshkov不稳定性、气体射流波系结构等复杂的物理过程.对于采用喷气推进的水下高速运载器而言,两相射流与空化是两个不可避免的关键问题.水下航行体的空化可分为自然空化和通气空化两类:自然空化是在高航速下,绕流产生的局部低压区压力低于液体饱和蒸汽压时形成;通气空化通过向没有达到自然空化压力的低压区内通入气体形成.一般而言,通气空泡泡内压更高,也更加稳定和容易控制,常用于改善水下航行器的局部水动力特性.其中,航行体肩部等其他部位的空化多属于自然空化,自然空化会在航行体表面形成很强的局部载荷,引起结构破坏和运动失稳.由发动机燃气流诱导形成的尾空泡则属于通气空化,其空泡在溃灭时引起的尾部压力脉动会造成发动机推力不稳定等问题.而目前国内外有大量关于两相射流和空化的独立研究,但关于两者耦合作用的研究却很少,尤其是外部流场流动状态下的两相射流问题.Karn等[1]对不同弗劳德数和流量系数下通气超空泡的闭合方式做了细致的研究,并讨论了阻塞带来的影响.Wosnik和Arndt[2]通过时间分辨粒子成像测速系统(PIV)对回射流引起的超空泡泡沫尾流进行了实验研究.施红辉等[3,4]对静水中气体射流的瞬态特性和初期流场进行了实验和数值计算研究,深入分析了射流结构、鼓胀与回击、几何尺寸等问题.Berna等[5]通过PIV技术对静水中高速气体射流所携卷水滴的速度分布进行了实验研究.对于水流中的气体射流,Krishnan[6]在前人研究的基础上,对射流和主流间的干涉规律进行总结分析;Makiharju等[7]和Rek等[8]则分别从实验和数值两个方面对射流的拓扑结构进行了研究.关于射流与空泡的耦合问题,Paryshev[9]在Efros经典回射流空泡闭合理论及独立膨胀原理的基础上,给出了不可压缩流体射流与空泡耦合作用下空泡闭合的数学模型,并总结了流体滞止压力比及动量比两个主要判据.Kirschner等[10]根据以上两个判据,将空泡中的气体射流分为“刚性”和“柔性”两类,通过文献[11]的实验结果对Paryshev的理论进行验证后,又进一步考虑了射流的推进效率问题.Kinzel等[12]通过数值计算,对射流与主动通气空泡的耦合作用进行了深入分析.何晓等[13]对喷气推进与空泡流耦合问题的尺度效应进行了数值计算研究,并与实验进行了对比.

本文通过水洞实验,研究了外部流场流动状态下回转体尾部超声速气体射流及其诱导尾空泡间的耦合作用,并结合空泡闭合理论模型,分析了不同类型诱导尾空泡的形成机理与转变条件.

2 实验方法

实验在哈尔滨工业大学HT-01型循环式通气水洞中完成,通过高速摄影对射流诱导尾空泡形态进行了研究,主要设备为高速摄像机、质量流量计和压力传感器.图1为水洞的整体示意图,为避免图像失真,水洞实验段为26 cm×26 cm×100 cm的长方体,前后上下四面均设有透明观察窗.在实验段下游设有气水分离罐,用以移除实验时通入的气体,保证通气实验可以连续进行.同时,通过空气压缩机和真空泵来控制气水分离罐内压力,结合实验段处的压力传感器,可以使来流静压保持恒定.实验段流速通过电磁流量计测得的实时水流量换算得到.其中,压力传感器精度为±1 kPa,量程为绝压0—200 kPa,电磁流量计精度±3 m3/h.图2(c)为实验方案整体示意图,其中两台高速摄像机型号分别为Photron FASTCAM SA-X和FASTCAMAPX RS,实验时拍摄帧率设置在3000 fps,曝光时间1/6000—1/3000 s,APX为时间同步主控机,SA-X为从机,两台相机分别从水平和垂直方向拍摄,摄影光源为四支1000 W钨丝灯.

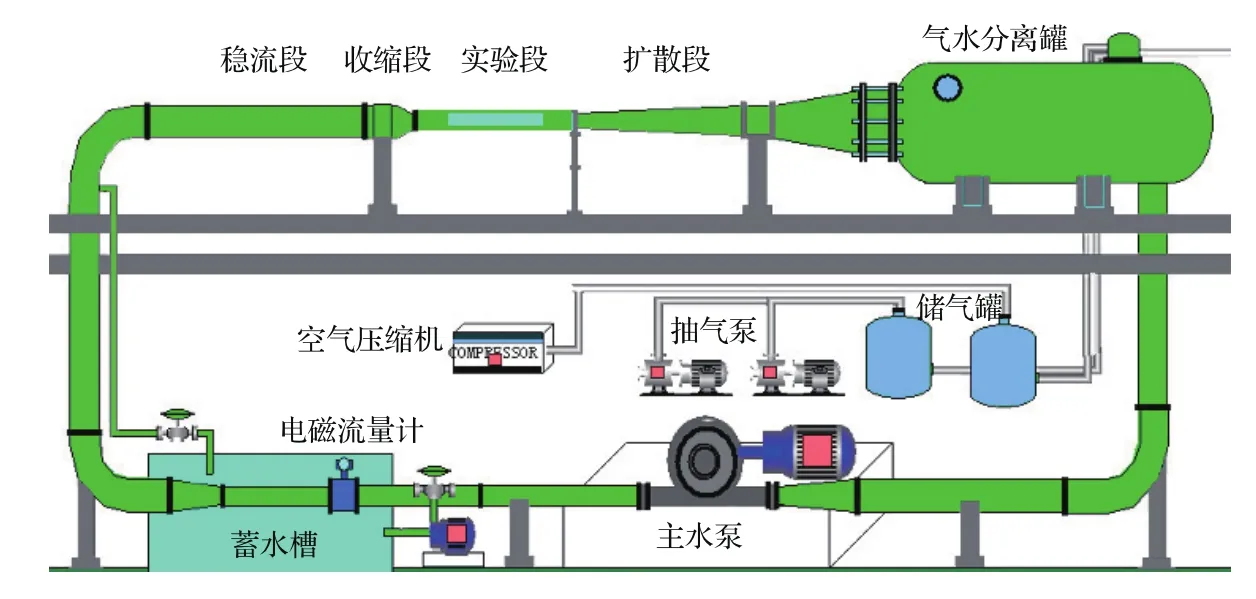
图1 HT-01型循环式通气水洞示意图Fig.1.The schematic of the HT-01 water tunnel.

用来发生气体射流的拉瓦尔喷管几何尺寸如图2(b)所示.其中,扩张段型面曲线采用基于特征线法的直声速线短化长度喷管方法设计.这种方法在保证低马赫数喷管流场品质的同时,可以使喷管长度较传统方法减少50%[14].综合考虑供气设备的供气能力,设置喷嘴喉部直径1.35 mm、出口马赫数2.45,通过计算得到扩张段扩张比2.54,出口直径2.15 mm.收缩段型面通过移轴维托辛斯基公式计算得到,移轴后收缩比为2.0,实际收缩比为4.4,入口直径6.0 mm.喷嘴通过3D打印技术成型,实测精度在±0.1 mm.喷管喷出气体的流量通过一台七星D07-23FM质量流量计测量,精度±3.8标准升/分钟(SLPM),并结合压力传感器测得的实验段静压和电磁流量计测得的流速,换算为与空化数相关的[15]描述空泡气体供给量的通气流量系数:

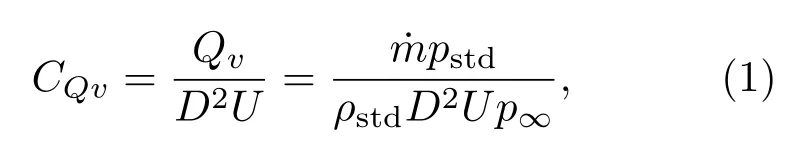
图2 (a)实验模型实物图;(b)喷嘴几何尺寸示意图;(c)实验方案整体示意图Fig.2.(a)Photograph of the test body;(b)the schematic of the jet nozzle;(c)the experimental setup.

其中,˙m为质量流量计测得的质量流量;pstd,ρstd分别为质量流量计标定时的标准压力和密度;D=40 mm为回转体直径;U,p∞分别为实验段来流速度和静压.对于本文所使用的压缩空气气源而言,若假设其在喷管中的流动过程是一维等熵的,则当管内发生壅塞时,喷管内气体质量流量˙m与入口滞止压力p0满足关系式

其中,At为喷管喉部截面积,T0=300 K为气体总温,γ=1.4为空气比热比,R=287 J/(kg·K)为气体常数.对于本文设计马赫数为2.45的喷管而言,当入口滞止压力与环境的压比(落压比)p0/pb＞2.3时出口流动达到过膨胀超声速状态,p0/pb＞15.8时达到欠膨胀.在已知质量流量的情况下结合(2)式和喷管出口环境压力,即可判断气体射流喷出时是否达到声速.外部流场流速通过弗劳德数Fr描述,其定义为

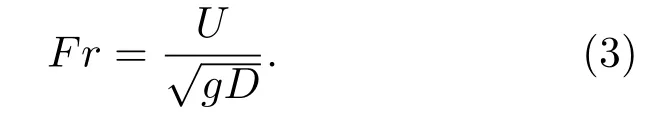
由于在外部流场冲击下的尾空泡瞬态特性强,通过对比特定时刻的图像不容易发现其形态特征变化的一般规律.为消除时间变量的影响,得到与时间无关的尾空泡形态特征规律,本文对部分工况下的图像转化为灰度值为0—1的灰度图像做了时间平均处理,平均处理后图片中对应像素点的灰度值为

其中,g(x,y)为像素点(x,y)处的灰度值,t为时间序列.

3 射流诱导尾空泡形态及其闭合方式

3.1 实验结果概述

实验中的自变量为外流场流速和射流质量流量,分别对应弗劳德数Fr和通气流量系数CQv,其中流速U范围为2—10 m/s,对应弗劳德数3.2—16.2,通气量范围0—114 SLPM,对应流量系数0—0.5,喷管最大落压比约14.0.实验段来流总压为控制变量,保持107 kPa不变,静压随流速变化,不同弗劳德数下来流静压见表1.实验时先调节来流至预设流速,再由小到大依次调节通气量,共观察到泡沫状、完整、部分破碎、脉动泡沫状4种形态的尾空泡.以Fr=6.5为例,随着流量系数的增加,空泡形态及闭合方式的演变过程如图3所示,全部工况下的尾空泡形态如图4所示.

到2017年下半年，感觉好了一些。在单位之外，基本上都在飞行，西藏、新疆、内蒙、贵州、浙江、河南等等。有一段时间，每到一地，或者从某地回来，最初几天，身体还莫名不适。很多时候，睡觉也是一件自觉恐惧的事情。一个人，侧着，蜷曲着，像微信朋友圈流传的那张，一个女孩蜷曲躺在白粉笔画的圆圈内的图片那样。有一次，和儿子睡在一张大床上，尽管是夏天，我发现自己睡得很安稳，一觉天亮不说，心里还跃动着一种说不清楚的幸福感。后来，儿子去绵阳读书，我去看他，晚上睡在宾馆，那种感觉，再次让我相信和感激血缘的无形力量。

表1 不同弗劳德数对应实验段来流静压Table 1.Inlet static pressure in the test section under different Froude numbers.

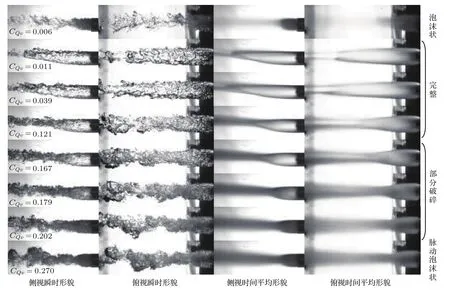
图3 Fr=6.47时尾空泡瞬时及平均形态Fig.3.The instantaneous and time averaged form of the jet induced tail cavity at Fr=6.5.

在流量系数较小时,尾空泡为泡沫状.此时喷管喷出的气体不足以维持单连通空泡的形成,其瞬时形态表现为大量聚集在回转体尾迹区内相互独立的气泡,并以游离气泡逃逸的方式自尾部泄气.由于光线在气泡间的多次折反射,此时的空泡在图像中表现为不透明的深色区域.当流量系数逐渐增大到某一阈值时,在各弗劳德数下的泡沫状空泡均会阶跃性地转变为单连通的完整空泡.此时尾空泡在形态上与通气超空泡后半部高度一致,闭合方式也相似,同样可以观察到回射、双涡、脉动等现象,如图3所示.这一阶段空泡的特点是不同流量系数下闭合方式的显著变化,以及由此带来的空泡长度改变.随着流量系数的继续增大,空泡尾部水气界面将在高速气体射流的作用下逐渐失去稳定性发生破碎,对光线的散射作用增强而变得不透明,演变为部分破碎空泡.对于Fr=3.2—9.8的三种状态,其空泡由完整转变为局部透明的过程有很强的阶跃性,而在Fr=13.0和16.2两种流速较高的状态下则是渐变过程,不存在明显的分界点.这一阶段空泡的特点是随流量系数增大长度逐渐减小,以及不透明区域所占比例逐渐增大.此后,尾空泡重新恢复到小气量时的泡沫状态,但喷管形成的高速气体射流形成贯穿整个空泡的泄气通道直接进入下游流场,空泡演变为脉动泡沫状.这一阶段空泡的平均形态随流量系数的增加几乎不变,始终保持脉动泡沫状空泡形成初期的形态与尺寸,只是泄气管道的平均宽度及其中气泡的尺寸随着流量系数的增加显著增长.

图4 气体射流诱导回转体尾空泡形态分布图Fig.4.Form map of the jet induced tail cavity.

图4为不同弗劳德数下尾空泡的形态随着体积流量系数的增加均依次经历了泡沫状-完整-部分的演变过程.其中,完整空泡形成的起始流量系数随着弗劳德数的增加而有所提高,即在高弗劳德数下,需要更大的通气量才能在回转体尾部形成单连通空泡.而部分透明空泡的起始流量系数则以Fr=9.8为拐点表现出了随弗劳德数增加而先增大后减小的趋势,在Fr＜9.8之前起始流量系数随弗劳德数的增加而增大,在Fr＞9.8后则开始减小.在Fr=3.2和6.5的两种流动状态下,当流量系数分别达到0.24和0.270时,空泡转变为脉动泡沫状.由于实验条件限制,在更高的弗劳德数下是否也存在脉动泡沫状空泡,还有待进一步探索.

3.2 泡沫状及完整空泡

所有四种形态空泡中,前两种在传统的通气空泡研究中已有详尽描述[1,16].典型工况下泡沫状空泡的形态特征如图5所示,这一阶段的体积流量系数多处在103量级,由于超空泡理论中计算流量系数时分母项多采用空化器直径,而本文在计算尾空泡时采用回转体直径,对应于空化器所形成空泡截面积最大处直径,因而本文中泡沫状空泡的流量系数要小于文献中超空泡的流量系数.回转体绕流过程中形成的尾涡及其脱落过程,对泡沫状的产生及形态特征有重影响.这一阶段回转体尾部低压区内在供气-泄气平衡条件下形成的空泡不足以阻止外部绕流发生流动分离,因而会在回转体尾部形成多个文献[17]中所述的一次及二次涡.由喷管进入回转体尾部的气体在尾涡的冲刷下被不断地击碎和卷入,无法相互融合形成完整空泡,因而此时空泡呈沫状.同时,由于尾涡的不断脱落及空泡边界处外部流场强烈的冲刷作用,致使大量游离气泡向下游逃逸,从而阻止了气泡在尾迹区内的堆积和空泡向下游的扩张,以及对流动分离现象的抑制.这一阶段空泡形态的形成机制如图7所示.图5空泡瞬时形态中泄气路径相对中心位置的偏离及图6空泡边界处不规则变形均反映了尾涡及其脱落对空泡的影响.而由图5右侧的时间平均形态可以看出,这一阶段空泡的几何尺寸受外流场流速变化影响并不大,只是在弗劳德数较低时受重力影响略有上飘.

不同弗劳德数下形成的典型完整空泡如图8所示.这一阶段空泡的形态及发展规律与超空泡几乎一致,只是在射流尾空泡的边界上存在明显的不规则波动,且波长随弗劳德数的增加而缩短.而Fr＜9.8时,空泡的上下边界波动的幅度和波长存在明显差异,如图8(b)和图8(c)两幅图中,上边界波动的幅度均明显大于下边界,且存在更多长波成分.根据经典流动稳定性理论[18],当重力场中两个密度不同的液体间存在剪切运动时,如果密度较大的液体处在较轻液体的上方,则其界面对于任意波长的扰动都是不稳定的,而对较重液体位于下方的情况而言,其界面只在扰动的波长足够小时才会失稳,但同时表面张力对大曲率的短波扰动有很强的抑制作用.对于本文的尾空泡而言,由于上游近壁面边界层中本身就存在剪切流动,因而在流动最先发生分离的空泡前缘边界上即存在明显的波动,而不像超空泡的边界那么平滑.这些扰动在向下游的传播过程中不断发展,最终导致空泡的破碎和孤立气泡的形成,使射流尾空泡具有很强的瞬态特性,如在图8(a)中,虽然在用肉眼观察时和在时间平均图像中都能看到明显的双涡管结构,而其实际瞬时形态是多个相互独立的气泡,且气泡的大小和形态都有很强的随机性.

图5 典型工况下泡沫状射流尾空泡Fig.5.The typical form of a foamy tail cavities.

图6 受到尾涡影响到空泡边界Fig.6.The cavity boundary affected by the wake vortex.

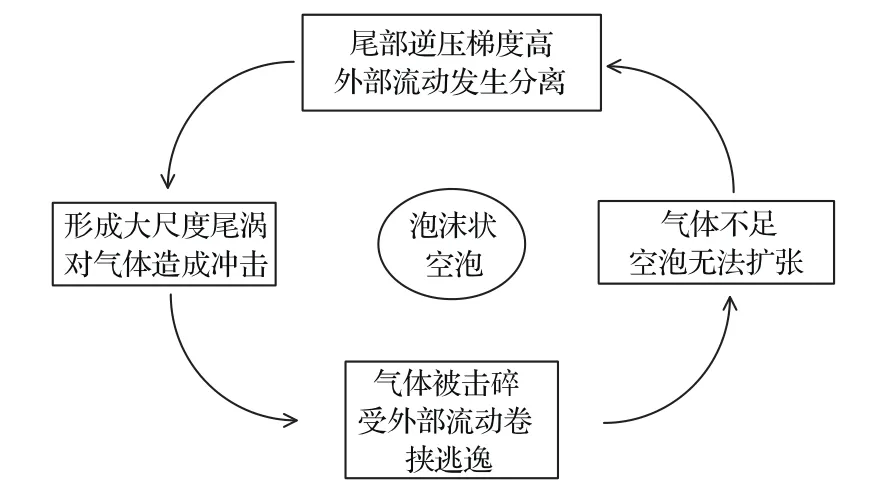
图7 泡沫状空泡形成机制Fig.7.The mechanism of foamy cavity formation.

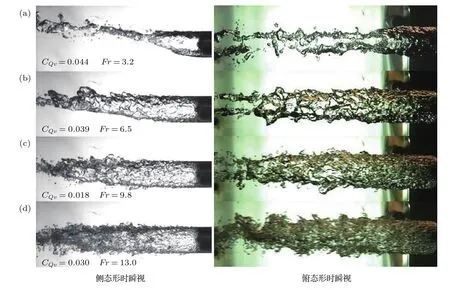
图8 典型工况下完整射流尾空泡Fig.8.The typical form of intact tail cavities.

3.3 部分破碎与脉动泡沫状空泡

部分破碎空泡与脉动泡沫状空泡为尾空泡在射流的作用下形成,与传统超空泡存在显著差异,其中,虽然超空泡也能观察到部分破碎的显现,但射流导致的空泡破碎在形态和成因上都明显不同.

各弗劳德数典型工况下形成的部分破碎空泡见图9.从图中可以看出,相对于弗劳德数的完整空泡而言,部分破碎空泡的后半部均发生了不同程度的破碎,变得不透明.图8中完整空泡的界面虽然也存在波动,但整体上依然保持连续,只产生少量的游离气泡,而部分破碎空泡的后部界面则完全破碎,产生大量尺寸较小的游离气泡,且不存在明显的闭合点.对于可以观察到闭合位置的部分破碎空泡而言,在弗劳德数相同时虽然其通气流量系数更大,但长度较完整空泡明显减小,且存在随通气流量系数增大而递减的趋势.

对于超空泡而言,其破碎大都由回射流和K-H不稳定性引起,在重力方向上具有较强的不对称性.而本文中较低流速的部分破碎空泡在重力和水平方向上都具有很强的对称性,如图9(a)和图9(b),说明此时的空泡破碎与空泡回射和重力失稳无关.但随着流速的增加,空泡的破碎在重力方向上逐渐表现出非对称性,如图9(c)和图9(d),说明此时稳定性对空泡的影响逐渐加强,因而在重力场中绝对不稳定的上界面会先于条件不稳定的下界面发生破碎.对于形成脉动泡沫状空泡前的部分破碎空泡,如图9(a)中Fr=6.5时,其泄气通道在靠近空泡闭合位置的区域上存在明显的常见于水下可压缩性射流的鼓胀和颈缩现象,如包含时间序列的图10所示.鼓胀和颈缩现象的发生,表明此时射流在冲出空泡时仍保持有较高的流速.

图9 典型工况下部分破碎射流尾空泡Fig.9.The typical form of partially break tail cavities.

图10 Fr=6.5时部分破碎空泡泄气通道的鼓涨和颈缩Fig.10.Bulge of the gas leakage path of a partially break tail cavity at Fr=6.5.

在Fr=3.8和6.5时观察到的脉动泡沫状空泡时序图如图11和图12所示.从两图中可以看出,此时的空泡具有很强的瞬态特性,其形状和尺寸较部分破碎空泡随时间变化更为剧烈.在空泡的后部存在一个由动量射流形成的气体通道,这与在静水中观察到的现象十分相似,但由于外部流动的作用,即使在Fr=3.2的低速状态下也无明显的浮力射流段.在靠近空泡的动量射流段则与静水中一样存在鼓胀与膨胀反馈等现象,而动量射流段周围环绕的泡沫状空泡则极大地减小了射流附近介质的密度,使本文中射流的动量段远长于静水中.关于此时环绕射流的脉动泡沫状空泡,虽然其瞬时形态无序性较强,但时间平均形态却与小气量时形成的泡沫状空泡几乎一致,且在瞬时表观细节上也极其相似,均为密集排列的小气泡群,如图13所示.高度的相似性,说明两种空泡很可能在形成机理上存在某种联系,如下文脉动泡沫状空泡转变机理分析中所揭示的.

4 射流诱导空泡形态分析

4.1 射流耦合空泡闭合理论

文献[17]中将与空泡耦合的射流分为三类:

2)中心射流在与空泡的耦合区域发生分离,部分从空泡中射出,部分沿空泡内边界发生回射,补充泡内气体,如图14(a)所示,此时p0f＞p0且J/Wc＞1/2,发生回射气体的流量qi满足

图11 Fr=3.2时脉动泡沫状空泡时序图Fig.11.The time series photographs of a penetrated foamy cavity at Fr=3.2.

图12 Fr=6.5时脉动泡沫状空泡时序图Fig.12.The time series photographs of a penetrated foamy cavity at Fr=6.5.

3)Efros闭合模型,中心射流不受空泡壁面阻挡,完全从空泡尾部射出,空泡闭合在中心射流上,沿射流边界的空泡关于对称轴的径向速度衰减为0,如图14(b)所示,此时p0f＜p0;

其中:p0和p0f分别为射流和来流的滞止压力(总压),J为射流的推力,Wc为空化器上的阻力.

由于本文中的射流马赫数较高,在考虑可压缩性后的滞止压力p0满足

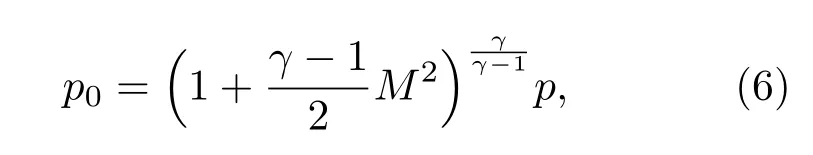
其中,γ=1.4为空气比热比,M为当地马赫数,p为当地静压.

射流的推力J为

其中,˙m为射流质量流量,ue为出口流速,pe为出口静压,p∞为环境压力,Ae为喷管出口截面积.将(1)式代入(7)式,可以推出J和CQv之间满足

图13 Fr=6.5时泡沫与脉动泡沫状空泡对比图Fig.13. The comparison between foamy and penetrated foamy cavity at Fr=6.5.

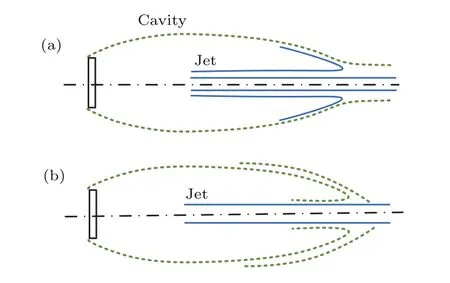
图14 两种射流耦合空泡闭合模型示意图Fig.14.Two models of the cavity closure onto a central Jet.

本文根据射流尾空泡的特点,做如下两个假设:

1)在尾空泡前缘起始点,外部绕流与固体表面的分离点处,空泡边界上流体质点关于回转体对称轴径向的速度分量为0,即其速度与对称轴平行,不存在径向膨胀或收缩速度;

2)不存在其他向空泡供气的气源,尾空泡内所有气体均来自于气体射流.

由于缺少空化器,因而对于射流尾空泡而言在物理层面上并不存在空化器阻力Wc这一概念.但根据尾空泡前缘边界上径向速度为0这一假设,可以进一步假定尾空泡在起始位置拥有最大横截面积,进而根据文献[19]中给出的最大空泡横截面积Sk与空化器阻力Wc的关系

计算出当前尾空泡对应的空化器阻力,其中,∆p为来流相对空泡内部的压力差,k≈0.96～1为常数,本文中取k=0.98.通过(6)—(9)式便可在射流尾空泡问题与Paryshev的理论模型间建立联系.

如不考虑射流流场的复杂性及流动过程中滞止压力的损失,以出射流口处的滞止压力作为p0与来流总压p0f进行比较,可以得到如图15所示的尾空泡形态分布图,其中p0根据(6)和(8)式得到.根据Paryshev提出的耦合模型,当p0f＜p0时射流将不受空泡阻挡,直接进入下游.结合关于射流尾空泡的假设2),以及在射流边界上剧烈的气-液掺混现象,可以得出p0f=p0应该是脉动泡沫状与部分透明空泡分界线这一推论.然而在图15中,p0f=p0却穿过完整空泡所覆盖的区域,且各阶段空泡的分布也缺乏规律,证明对于与超声速射流耦合的空泡而言,必须对射流的空间结构予以考虑.

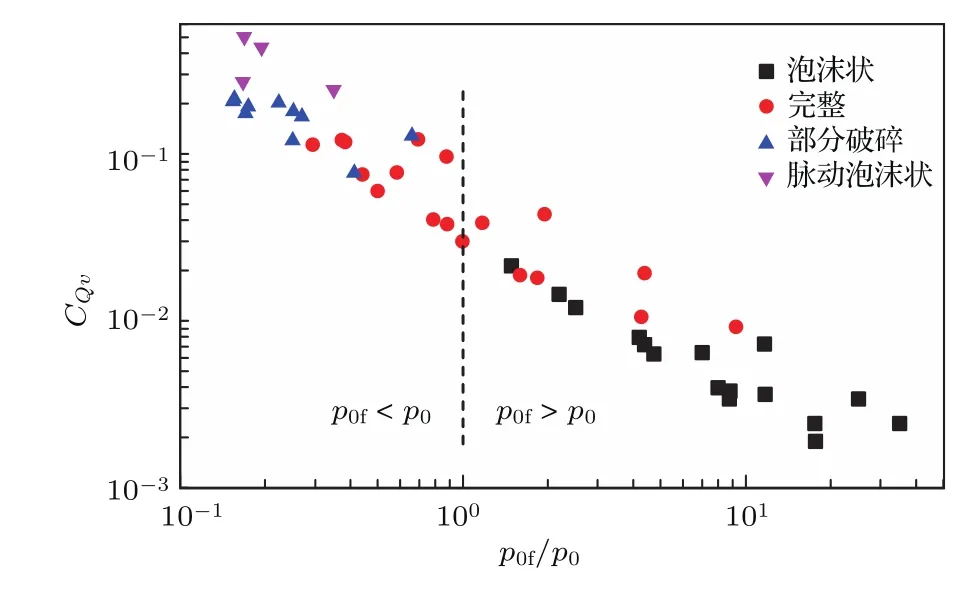
图15 关于滞止压力比和流量系数的射流诱导尾空泡形态分布图Fig.15.Form map of the jet induced tail cavity regarding total pressure ratio and ventilation rate.

4.2 脉动泡沫状空泡形成机理

为了能更准确地呈现超声速射流的空间流场结构,尤其是射流流动过程中压力、速度等物理量的变化,从而更好地阐明超声速射流耦合尾空泡的形成机理,本文对各工况下的射流流场结构进行了数值求解.由于水下超声速射流是一个强瞬态问题,要实现对实验工况的覆盖计算成本过高,不适宜作为实验的辅助分析手段,并且已发表的有关水下射流的文献,也多针对静水流场,对于本文外流场流动状态下射流尾空泡问题的参考价值有限,因而本文通过数值计算与理论模型相结合的方法,对实验现象进行分析.对于业已形成的尾空泡的射流而言,由于理论模型中射流与空泡耦合作用下的流动状态仅与二者的总压有关,在直接接触前不考虑它们之间的相互作用,所以数值计算直接以空气中射流的计算结果作为理论模型中总压判据的输入参数.

数值计算域边界条件设置及环境压力100 kPa喷嘴入口流量100 SLPM下射流马赫数分布计算结果见图16.计算采用二维轴对称模型,计算方法参考文献[20],选用k-ωSST湍流模型及二阶迎风格式求解.由于空气中气体射流的CFD计算技术已经非常成熟,因而此处直接引用了文献中的计算方法,没有针对数值计算设计专门的验证实验.介于计算域内包含有速度极低的亚声速流动区,本文采用基于压力的SIMPLE求解器而不是密度基求解器求解.

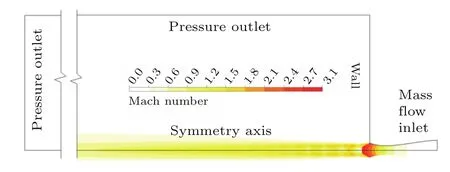
图16 数值计算边界条件设置Fig.16. Boundary condition setup of the numerical simulation.

将从实验中得到的时间平均空泡形态与数值计算得到的结果相叠加后,可以得到如图17和图18所示图像,其中的彩色流线为按(6)式数值计算得到的射流滞止压力.结合Kirschner的空泡-射流耦合理论[14],在黑色等值线p0f=p0内部,射流滞止压力大于外部流动滞止压力,射流属于“刚性”的范围,空泡在这一区域上的闭合方式满足Efros闭合模型,而等值线外部射流表现为“柔性”.联系4.1节中假设2),当空泡闭合在“刚性”射流上时,射流将不受空泡的阻拦直接进入下游,这样空泡将由于气体无法得到补充而溃灭,即空泡闭合点与“刚性”射流的相对位置决定空泡能否维持.这一推论在Fr=6.5和3.2两个空泡发展历程较为完整的弗劳德数下可以得到清晰的验证.在图17(c)和图18(a)中部分破碎空泡在转变为脉动泡沫状空泡前的示意图中可以看出,此时射流的“刚性”区域远端与空泡的闭合点已几乎处于同一位置,射流通气量小于此状态时空泡得以维持,大于此通气量时则溃灭为脉动泡沫状,正好对应于射流“刚性”区域完全位于和部分超出空泡内部两种情况,证明了上述推论的正确性.同时也解释了图13脉动泡沫状与泡沫状空泡在平均形态和表观细节上高度一致的现象,即这两种空泡有相同的成因,都是空泡供气不足造成,都适用于图7中的形成机制.

图17 Fr=6.5时射流滞止压力与空泡闭形态示意图Fig.17.Composite picture of stagnation pressure and cavity form at Fr=6.5.

图18 Fr=3.2时射流滞止压力与空泡闭形态示意图Fig.18.Composite picture of stagnation pressure and cavity form at Fr=3.2.

对于Fr=9.8/13.0/16.2三个没有出现脉动泡沫状空泡的弗劳德数而言,当其流量系数达到最大时,由于射流“刚性”区域仍然位于空泡以内、闭合点之前,因而依然能维持在部分破碎状态,如图19所示.在流速较低的图19(a)中,虽然在时间平均图像中空泡已经闭合在射流的“刚性”区域上,但从连续的录像中可以看出,此时的空泡长度有伴随时间的明显变化,即在部分时刻空泡是完全包裹射流“刚性”区域的,因而能够维持一定形态的空泡.而随着流速的增加,流动稳定性对空泡气水界面的影响变得显著,如在图19(b)和图19(c)中,虽然在本实验的视域内已无明显的空泡闭合点,但由于流速增加造成的界面失稳,在空泡的后部依然形成了大面积的深色区域.

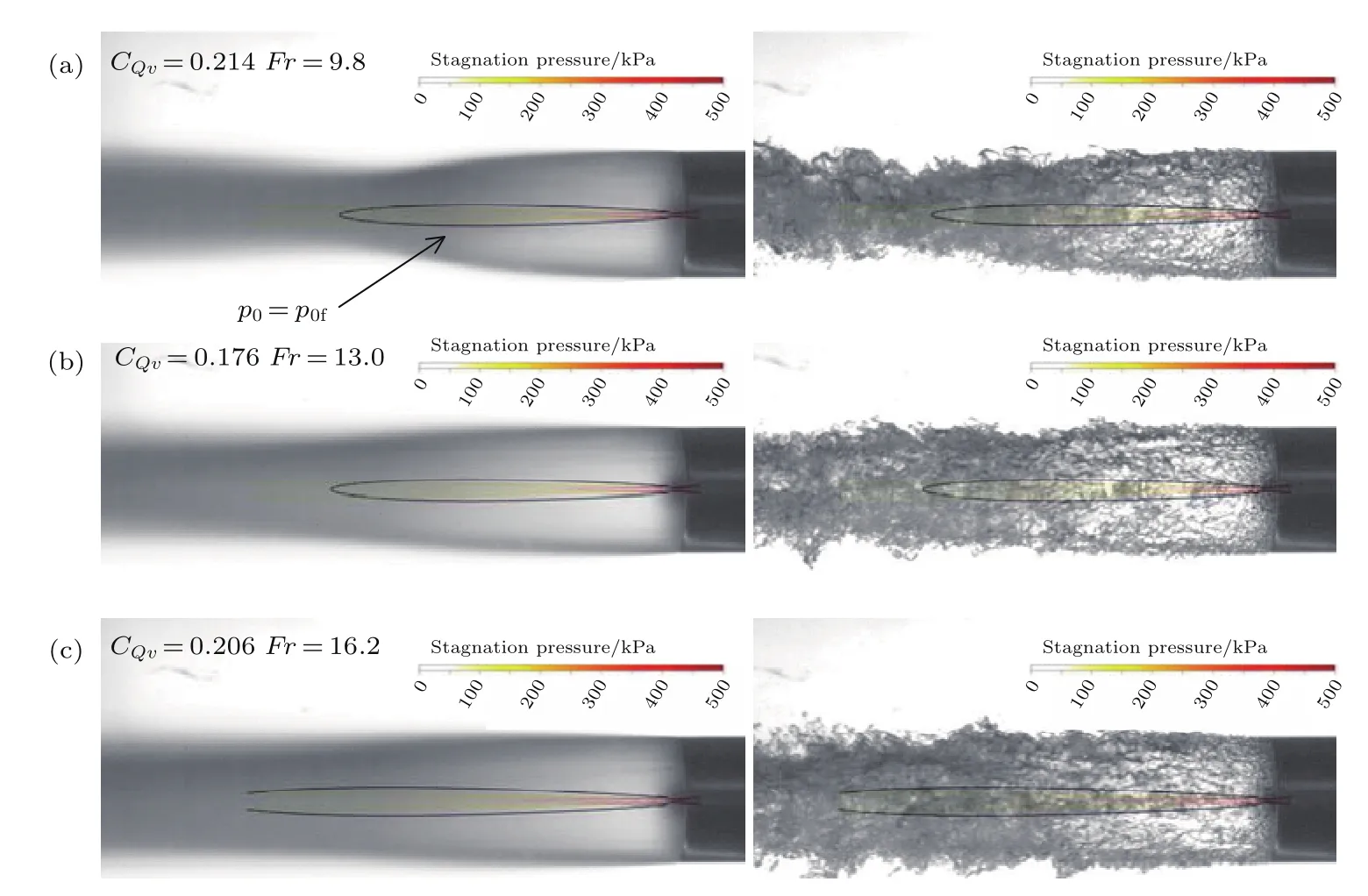
图19 大弗劳德数下下部分破碎空泡射流滞止压力示意图Fig.19.Composite picture of stagnation pressure and partially break cavity at larger Fr numbers.

4.3 部分破碎空泡形成机理

对于完整空泡向部分破碎空泡转变的过程,由于本实验缺少泡内压即空泡数的测量,因而无法通过(9)式计算各尾空泡对应的空化器阻力,进而通过(5)式来判断.在这里引用文献[21]所述实验中两组与本文Fr=6.5时工况较为接近的数据来对(5)式进行验证.文献[17]中模型的几何外形和尺寸以及喷嘴出口马赫数与本文相同,且在尾部布置了压力传感器.这两组数据的内容与根据(5)和(9)式得到的计算结果见表2,对应的空泡形态见图20.

表2 实验[21]中数据及计算结果Table 2.Data from experiment[21]and calculation.

从形态上可以看出图20(a)和图20(b)分别对应图3中Fr=6.5时部分破碎空泡的起始和结束状态,而此时通过计算得到回射气体的占比qi/q0分别为0.86和0.35,通过空泡的实际流量系数换算式

得到图20(a)和图20(b)中空泡对应的实际流量系数分别为0.104和0.077,即图20(b)中的实际通气更小,这与其较小的空泡尺寸相符合.图20(a)中回射气体的占比qi/q0为0.86,即只有14%的气体直接射出了空泡边界,处于部分破碎空泡的起始阶段,Fr=6.5时完整空泡向部分破碎空泡转变的体积流量系数CQv=0.12—0.17,正好处于此范围内,证明了(4)式对完整空泡向部分破碎空泡转变判定的正确性.

图20 实验[21]中两组空泡瞬时与时间平均形态Fig.20.The instantaneous and time averaged form of the cavities in experiment[21].

虽然图20(b)中的实际通气量较小,但依然远大于Fr=6.5时完整空泡的下界CQv=0.01,然而此时其尾空泡的平均外部轮廓已非常接近图3中完整空泡形成前的泡沫状空泡.如果按(4)式计算的实际通气量是准确的,当前通气量在忽略射流流动的情况下应当形成透明的部分破碎空泡,而实际此时在瞬态图像中仅偶尔能观察到透明的空泡,在时间平均图像中空泡则变为完全不透明.即对某一特定时刻而言,受到气体射流与空泡强瞬态耦合作用的影响,空泡的形态是不确定的,可能为部分破碎空泡,也可能完全破碎为脉动泡沫状,而其平均形态则表现为脉动泡沫状,所以(4)式在回射气量较小及接近脉动泡沫状时计算的准确性还需在考虑射流瞬态特性的条件下进行更细致的研究.

5 结 论

通过水洞实验研究了流动状态下射流诱导尾空泡的形态特征,并分析了形成机理.实验发现,根据射流滞止压力及动量的不同,水流中回转体尾部气体射流诱导产生的尾空泡至少有泡沫状、完整、部分破碎、脉动泡沫状四种可能的形态.其中,泡沫状与完整空泡的特征与传统超空泡一致,部分破碎诱导空泡的对称性则明显区别于超空泡,而脉动泡沫状空泡则为射流诱导尾空泡所特有;当完整空泡在闭合区域被射流击碎向部分破碎空泡发展时长度会逐渐减小;脉动泡沫状空泡拥有与泡沫状空泡相同的时间平均形态及成因,但瞬态特性更强.气体射流受液体阻挡后回射进入空泡所对应的实际通气流量系数是控制空泡形态的关键因素:气体射流全部被空泡阻挡时,诱导空泡特征与通气空泡一致,为泡沫状和完整空泡,仅受射流对应流量系数的单向影响,耦合作用弱;气体射流部分受空泡阻挡发生回射时,形成部分破碎空泡,射流与诱导空泡间耦合作用强烈,空泡实际流量系数由多个因素的动态平衡决定;气体射流不受阻挡直接进入下游时,形成脉动泡沫状空泡,此时射流气体仅有少量因掺混作用进入空泡,空泡对射流的影响减弱.对于强耦合状态下的部分破碎空泡,其向完整和脉动泡沫状空泡转变的临界点与Paryshev提出射流空泡耦合模型的预测结果一致,且形态变化规律与实际流量系数理论估算值相符合.

由于条件限制,本文中射流的最大流量及滞止压力较小,在高流速下无法得到完整的空泡发展历程.在后续的研究中,可以进一步对大推力射流诱导空泡间的耦合作用进行研究,并加入对空化数和推进效率的测量,从而对射流诱导尾空泡进行更细致的定量分析.

[1]Karn A,Arndt R E A,Hong J R 2016J.Fluid Mech.789 259

[2]Wosnik M,Arndt R E A 2013J.Fluids Eng.135 011304

[3]Shi H H,Wang J F,Chen S,Dong R L 2014J.USTC233(in Chinese)[施红辉,汪剑锋,陈帅,董若凌 2014 中国科学技术大学学报233]

[4]Wang C,Shi H H,Wang J F 2016CIESC J.67 2291(in Chinese)[王超,施红辉,汪剑锋 2016化工学报 67 2291]

[5]Berna C,Julia J E,Escriva A,Munoz-Cobo J L,Pastor J V,Mico C 2017Exp.Therm Fluid Sci.82 32

[6]Kishnan M 2013Annu.Rev.Fluid Mech.45 379

[7]Makiharju S A,Lee I H R,Filip G P,Maki K J,Ceccio S L 2017J.Fluid Mech.818 141

[8]Rek Z,Gregorc J,Bouai fiM,Daniel C 2017Chem.Eng.Sci.172 667

[9]Paryshev E V 2006J.Eng.Math.55 41

[10]Kirschner I,Moeny M,Krane M,Kinzel M 2015J.Phys.:Conference SeriesLausanne,Switzerland,December 6–10,2015 p012156

[11]Moeny M,Krane M,Kirschner I,Kinzel M 2015J.Phys.:Conference SeriesLausanne,Switzerland,December 6–10,2015 p012162

[12]Kinzel M P,Krane M H,Kirschner I N,Moeny M J 2017Ocean Eng.136 304

[13]He X,Lu C J,Cheng X 2010J.Hydrodyn.367(in Chinese)[何晓,鲁传敬,陈鑫2010水动力学研究与进展:A辑367]

[14]Yi S H 2013Supersonic and Hypersonic Nozzle Design(Beijing:National Defense Industry Press)p77(in Chinese)[易仕和 2013 超声速与高超声速喷管设计(北京:国防工业出版社)第77页]

[15]Zhang X W,Wei Y J,Zhang J Z,Wang C,Yu K P 2007J.Hydrodyn.19 564

[16]Kawakami E,Arndt R E 2011J.Fluids Eng.133 091305

[17]Spazzini P G,Iuso G,Onorato M,Zurlo N,Di Cicca G M 2001Exp.Fluids30 551

[18]Drazin P G,Reid W H 2004Hydrodynamic Stability(Cambridge:Cambridge University Press)p17

[19]Logvinovich G V 1972Hydrodynamics of Free-boundary Flows(Jerusalem:Israel Program for Scienti fi c Translations Ltd.)p109

[20]Zhao F,Zhang Y L,Zhu R,Wang H 2014J.USTB36 366(in Chinese)[赵飞,张延玲,朱荣,王慧2014北京科技大学学报36 366]

[21]Zhang X S,Xu H,Wang C,Lu H Z,Zhao J 2017Acta Phys.Sin.66 054702(in Chinese)[张孝石,许昊,王聪,陆宏志,赵静2017物理学报66 054702]