浅谈初中数学的一题多解教学

葛 剑（湖南省双峰县荷叶镇宝农学校，湖南 双峰）

何谓一题多解？顾名思义，一题多解是指解题者在面对一道多解题时能够从不同的角度、不同的方位、不同的层次去审视、分析、解构其中包含的数量关系、空间关系、逻辑关系等，以做到用不同的解法求得正确的结果。一题多解具有挑战性，是初中数学教学中的宝贵资源，教师应当善于设计这类题型的教学，学生也当敢于、乐于直面这类题型的挑战。

一、一题多解在代数教学中的应用

代数几何是初中数学的重要部分，也是初中学生经常接触的内容。将一题多解应用到代数教学中，可以夯实初中生的数学基础，强化初中生的数学运算能力，提升初中生在面对千变万化的数字时的统筹综合思维和逻辑灵活性。在《因式分解》的教学中，教师可以一例展开教学：

某小区规划在边长为x的正方形场地上，修建两条宽为2 m的甬道，其余部分种草，要求用多种方法计算甬道所占的面积。

这个多解题也是一个数形结合的题目，难度较低，但仍存有一定的抽象性。教师可以组织一个较短的时间，在有限的时间内展开头脑风暴，让学生们独立地或合作地解题。学生群策群力，在草稿纸上画来画去，最终获得了不少于3种的解题思路：（1）根据甬道自身进行矩形面积计算；（2）将甬道等量移位，挪到正方形的边上，然后减去草地部分的面积；（3）假定两条甬道处在正方形的正中位置，用总面积减去4个全等的草坪面积。对应地，解题过程如下：（1）2x·2-2×2=4x-4；（2）x2-（x-2）2=（x+x-2）（x-x+2）=（2x-4x-4。这种伴随式的一题多解教学，时效性很强，充满了弹性，也充满了活力，可以使学生的数学学习由浅入深，更加高效。

二、一题多解在平面几何中的应用

平面几何教学是以平面图形为主的教学，融合有公式、定律等数学知识，涉及图形的数量关系和空间位置关系，数形结合，变化多端。一题多解在平面几何教学中的应用教学，教师可以以下题为例展开。

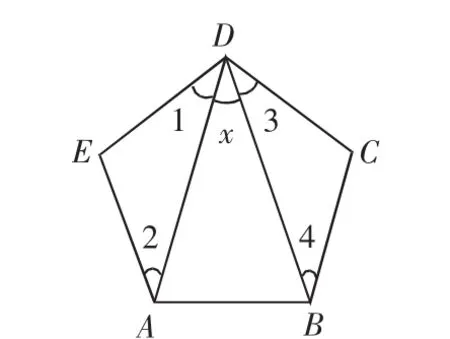
如图，五边形ABCDE的内角都相等，且∠1=∠2，∠3=∠4，求x的值。这道题涉及到了五边形、三角形的内角和，并藏有三角形全等的知识，教师可以在适当的课程中切入这个一题多解的案例，并组织学生每两人一组，合作解题。学生会先行讨论可能存在的解题思路，随后分别展开解题。

如甲同学的解题过程为：

∵ 五边形 ABCDE 的内角都相等，∴∠C=（5-2）×180°/5=108°=∠E。

∵∠1+∠2+∠DEA=180°，∴∠1+∠2=72°。

又 ∵∠1=∠2，∴∠1=36°。同理，∠3=36°。

又 ∵∠1+∠2+∠x=108°，∴∠x=36°。

而乙同学的解题过程则为：

∵ 五边形 ABCDE 的内角都相等，∴∠C=（5-2）·180°/5=108°=∠E=∠EAB。

又 ∵∠1+∠2+∠DEA=180°，∠1=∠2，∴∠2=36°

∵∠2+∠DAB=∠EAB=108°，∴∠DAB=72°。同理，∠DBA=72°。

∵∠DAB+∠DBA+∠x=180°，∴∠x=36°。

有的学生在寻求新的解题思路的过程中，还在三角形全等、等腰三角形、设计辅助线等方面做了有益的尝试。如此，一题多解的教学和合作学习完美融合，在紧张而活泼的氛围中，学生的数学思维得到了有效发散，他们的团队合作、取长补短的意识也得到了强化。

三、一题多解在动手操作环节中的应用

初中数学动手操作环节相比较而言更加综合，一题多解在这个领域的应用，除考验学生一定的公式、定律基础外，还考验学生的动手操作能力以及空间思维发散能力。例如，在《综合与实践长方形包装盒的设计与制作》中，教师可以以“设计竞赛”的形式落实一题多解的教学。同样，学生分组合作设计制作长方形包装盒，从绘制的平面设计图上看，有的组是“中心开花式”的设计，然后把四个侧面树立起来，完成制作；有的组是“平推式”的设计，主要部分的设计集中在一侧，然后或者从左到右，或者从上到下地完成剩余部分的设计，就像是设计了一套衣服一般，最后从另一侧“卷”过来，完成制作。如此，学生的空间思维和组织能力将在一题多解的动手操作实践中得到检验，他们换个思路、方向解决问题的数学思维也将得到有效的发散。

综上所述，一题多解作为初中数学教学中的宝贵资源，应当受到师生的共同重视。在具体的一题多解教学中，教师应当灵活采用不同的教学理念和方法途径，去实现代数、平面几何、动手操作实践等多方面、多领域的多元化教学，实现不同解题思路和方法的传授，从而充实初中数学课堂，大幅度提高教师的教学质量和学生的解题效率，提升初中生的独立思考和推理分析能力，提升初中生综合已学知识、活学活用触类旁通的能力，使初中生的数学素养得到显著的增强。