用表格法解决初中数学应用题的研究实践
徐 妍
(广东省中山市黄圃镇中学,广东 中山)
一、问题的提出
初中数学应用题是学生普遍感觉到难的问题。笔者曾做过调查,两个班90名学生,愿意做应用题的不超过20人,喜欢做的更是少之又少。有些学生在小学就已经对应用题产生畏惧心理,看到较多文字就已感到束手无策。很多人只是通读文字而不能理解意思。升入初中后,由于应用题的难度逐渐提高,隐含的逻辑关系更加复杂,再加上初中理解应用题的一般方法是设未知数、列方程,这就更使得学生感到极大的不适应,对应用题的畏惧感也与日俱增。具体表现为:①设未知数时,用未知数来表示相关量不熟练;②抓不住等量关系;③找出等量关系后又不会列方程;④分析问题时,缺乏整体意识等。
二、研究实践
1.研究设计
(1)研究界定
表格法:就是通过列表理清有关列方程(组)解应用题的题目中的各条件和各数量之间的关系,从而帮助解题者审清题目的一种方法。表格由M行N列所组成,而其中每格中的数据可称为表格中的元素。表格具有简洁、直观、系统和有趣的优点,能化繁为简、化难为易,对比性强,一目了然。
初中数学应用题:应用题是将所学知识应用到实际生活实践的题目。应用题一直都是数学学科的重点和难点,目前教学大纲对学生解答应用题的能力提出了较高的要求。我们将研究范围限定于初中学段的数学应用题。
(2)研究方法
经验总结法、实验法、个案研究法。
2.研究实施
(1)表格建模
基于经验总结法,将初中数学应用题归类,进行表格建模。得到表1。

匹配问题:物品一 物品二每数共调配问题:情况一 情况二原有调配现有积分问题:情况一 情况二胜负平总计

表1 初中数学常见的七类应用题表格模型
(2)表格法应用实验
选取任教的两个班级作为实验对象,前测分数均值基本相当,可以认为学生的学习能力和学习水平基本相当,一个班为实验组,另一个班为对照组。教学内容为初中数学的典型应用题,教学结束进行后测。
表格模型的应用步骤分两步:
一审题,确定本题属于哪一类型题目,包括行程问题、工程问题、数字问题、利润问题、匹配问题、调配问题、积分问题。
二填表,先填上已知关系量、再确定设未知量,然后表示其他相关量,并找出已知条件中表示等量关系的一个语句,列出方程,将表格填写完整。
(3)表格法应用法则
笔者和学生一起总结出了“三二一”法则。以下列举“三二一”法则的应用。
例1行程问题:某班的学生到距学校15千米的地方秋游,一部分学生骑自行车先走,40分钟后,其余学生乘汽车去,结果同时到达,已知汽车的速度是自行车的三倍,求汽车的速度。
三个量:路程、速度、时间。
两种情况:乘汽车的学生、骑车的学生。
一个等量关系:骑车学生的时间-乘汽车学生的时间=40分钟。
将找到的“三二一”填入表格并完善。(设骑车速度为x)

表2 表格法应用示例1行程问题
根据等量关系得到:15/x-15/(3x)=2/3。
例2工程问题:一件工作,甲单独做6小时完成,乙单独做12小时完成,丙单独做18小时完成,若先由甲、乙合做3小时,然后由乙丙合做,问乙丙还需几小时完成。设乙丙还需x小时完成。
三个量:工作量、工作效率、工作时间。
鉴于不同模式的矩阵对环境有不同的适应性和选择性,必须要从职责分工、系统支持和团队文化等方面进行密切配合。①明确总体、专册所在专业处及专业室、设计院总部和专业处副总工程师的职责分工,强调总体在数据管理、计划编制和执行管理,以及进度控制方面的职责,并在生产指挥上给总体以充分授权,全力维护总体指令的权威;②加强勘察设计信息化建设,保证总体能够对设计计划、设计流程、设计任务与人员的匹配、设计资料互提等进行全过程管控,努力实现各专业网上协同设计和管理信息化;③培育开放式的内部文化,倡导各专业处及专业室之间、总体组内部建立良好的横向沟通协作文化,为总体开展优质高效的沟通奠定基础。
两种情况:甲乙合作、乙丙合作。
一个等量关系:工作量之和等于1。

表3 表格法应用示例2工程问题
根据等量关系得到:3(1/6+1/12)+(1/12+1/18)x=1。
例3匹配问题:某车间28名工人生产螺钉和螺母,每人每天平均生产螺钉12个或螺母18个,一个螺钉要配两个螺母。为了使每天的产品刚好配套,应该分配多少名工人生产螺钉,多少名工人生产螺母?
设生产螺钉的工人数为x。
三个量:每名工人生产数量、工人数、总生产数。
两种情况:螺钉、螺母。
一个等量关系:螺母数量是螺钉数量的2倍。

表4 表格法应用示例3匹配问题
(4)表格法应用效果
将测试分数进行比较,讲授了表格法的实验组与未讲授表格法的对照组分数存在显著差异,实验组平均分明显高于对照组。选取A班中的某生C讲授表格法前后分数也有明显差异,前三次测验平均分81.67,后三次平均分94.0,提高了12分。学会表格法解应用题之后,面对应用题测试,学生变得明显轻松自信,效果明显。实验证明,学生应用表格法能够比较快乐地、高效地解决数学应用题,收效良好,很好地突破了这个难点。
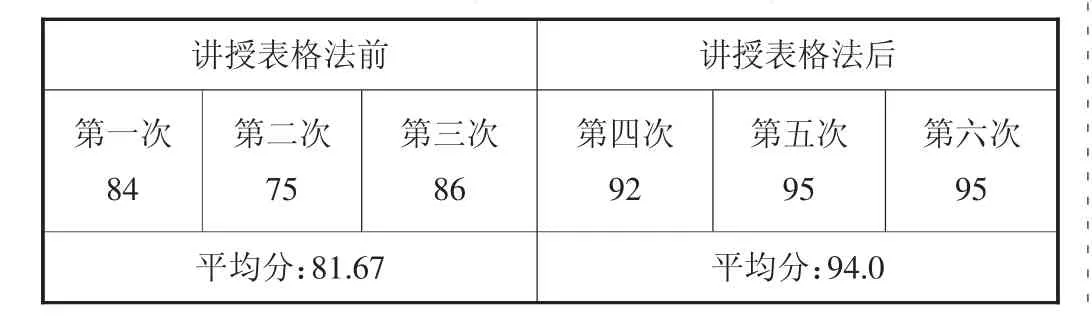
表5 A班某生C应用题测验成绩
(5)表格法应用小结
实践发现,表格法的优点表现在:
①帮助学生读题,攻破“题意关”。
应用题一般涉及的数量关系较多,关系复杂,学生有时读了很多遍题,仍觉大脑一片空白,不知所云。通过列表,学生可将题目背景中所涉及的已知数量和未知数量进行梳理,并将其分门别类,展示在表格中,让学生对题目的中心思想有一个准确的把握,攻破“题意关”。
②帮助学生分析,攻破“思路关”。
列出表格后,下一步重要工作就是要将相关数量用代数式表示出来。学生会将题中的已知数量直接填写在表格内,对于未知数量,学生会考虑选择哪个未知量设未知数,其余量又如何用含未知数的代数式表示。这无形中给学生提供了思维的顺序,帮助学生理清思路。
③帮助学生寻找隐性等量关系,攻破“难点关”。
有一些应用题其等量关系很明显,我们称之为“显性等量关系”,这种等量关系学生在读题后很容易找到;有些等量关系隐含在题意之中,我们称之为“隐性等量关系”,这种等量关系学生不易找到。借助表格,找“隐性等量关系”往往事半功倍。
在表格法的实际应用过程中,学生表现出如下一些问题:
①部分学生语文理解能力较差,当题目中出现了很多量,学生就分不清应用哪个模型。即使能分清用哪个模型,有时也无法识别哪个数代表的是哪个量,最终导致无法顺利填表。
②表格法解应用题大多数时候是竖着表示,横着列式。部分学生会思维固化,遇到竖着列式的题时不会变通。
③虽然草稿上已经理清等量关系,但有学生因为原来的思维设错未知数,最终导致解题错误。
④当表格中的情况分成几个阶段时,就会出现表格中套表格的情况,这个时候学生不容易处理。
三、研究小结
1.创新之处
在以前解应用题的过程中,学生的解题习惯比较容易停留在“想”上,但又想不清楚。通过表格法,可以把自己思考的过程明明白白地写出来,看得见,“无形”变“有形”。抽象的关系变为具体的符号,有利于自己判断审题是否正确。实践证明,在应用题的教学中运用表格的分析方法是分析数量关系、解决问题的有效途径,它让已知的、未知的量都参与到了解决问题的核心——列关系式,这是用算式解法无法比拟的优势。
表格法的创新之处在于,帮助学生将应用题中所蕴含的逻辑顺序、逻辑关系理顺、理清,从而极大地降低解题难度,使得学生解应用题变得轻松而富有成就感,大大提高学生的学习自信。
2.存在的问题
表格法的创新,大大降低了应用题的解题难度。但也出现了一些问题:
(1)有部分学生思维固化,只会套用模型,不会自己独立分析,以基础较薄弱的学生居多。因此,应用表格法时,不能忽略学生解题能力的培养。学生的解题能力用题海战术、死记硬背的机械记忆是培养不出来的。不应强求学生对表格模型的机械记忆,而应强调的是表格模型的理解与运用。应倡导的是“授之以渔”,而非“授之以鱼”。实际表现看,学生解题的错误,一般是由于理不清应用题中的逻辑关系造成的,表格法恰恰可以帮助学生理顺其中的逻辑关系,这才是表格法的意义所在。
(2)学生都有多年积累的经验,特别是对于基础较好的学生,用最简单、最易操作的方法来解决问题,并不一定强求用表格法。学生的解题方法是悟出来的,而非教出来的。解决问题的策略是多样化的,只要“殊途同归”就好。

