客随主“变”——浅谈数学习题课的学生主体地位

宋 菁

（浙江省杭州市余杭区信达外国语学校，浙江 杭州）

意大利瑞吉欧幼儿教育创始人罗里斯·马拉古奇的名师《儿童一百种语言》中写道：

孩子，是由一百组成的。

孩子有一百种语言，一百只手，一百个念头，一百种思考、游戏、说话的方式；

一百种，总是一百种倾听、惊奇和爱的方式，一百种歌唱与了解的喜悦。

一百种世界，等着孩子们去发掘；

一百种世界，等着孩子们去创造；

一百种世界，等着孩子们去梦想。

这首诗告诉我们，孩子是一个具有个性化的独立体，在教学中给他们一个独立的舞台，倾听他们的声音，他们就会散发灿烂的光芒。

传统的教师讲、学生听的课堂模式只适应于知识增长比较缓慢的时代，局限了学生个性化的发展，随着社会的发展，教育理念的更新，学生的自主学习能力也逐渐增强，教学过程中遵从学生的认知水平发展以及学习的主导地位显得愈加重要，在快速发展的今天，知识的补充越来越多，这些补充需要自我的学习和消化，因此学生学习的主体地位越来越明显，只有学生真正参与备课，参与课堂过程，参与课后评价，才能真正产生主人翁意识、高度的责任感，从而做到更有效地提升。然而数学课堂出现最多的还是习题教学，那么在数学习题课中，如何体现学生的主体地位呢？

一、以学定教——题目的挑选要来源于学生

传统的习题课备课是由教师一人完成的，课堂上学生对题目的呈现可能会有一种莫名的陌生感，或者说和原有知识的联系需要一段时间的缓冲。如果能在备课过程中提高学生的参与度，那在课堂教学中可以缩短学生的角色进入事件，更能勾起学生的挑战欲望，提高学生学习的兴趣。

一般习题课放在一个章节结束以后，在习题课前我会布置任务，让学生将一周的学习重点、难点及易错题找出来，俗话说“知己知彼，百战百胜”，让学生自己收集好本周的重点题型以及难题和易错题，让学生带着准备好的问题去听这堂习题课，对问题的有效解决更有利，学生的兴趣也更浓。至于课堂题目的选取，以小组的形式进行分工，组员为四人一组，成绩好的和数学比较薄弱的搭配在一起，利用自修时间分析重难点及错题情况，尤其是错题，要分析清楚错误的原因是什么以及解决这道错题的基本方法是什么，成绩好的给成绩差的进行讲评，这样组员都清楚了解到自己的薄弱环节，便可决定该组下一步该找怎样类型的题目展现在习题课上。分头收集完错题、难题后一起将收集来的例题进行一个挑选。筛选出三道比较重要的习题代表自己组的思想。最后组员将这三道题都一一去解决，为后面的上课做好准备。例如，我现在任教的是九年级，在复习完“圆”的知识以后，我们进行了圆的测试，在小组的归类讨论下发现组员对一些有关圆中的求线段长度掌握不够好，关于求最小值、最大值问题没有什么思路以及点的路径长存在问题，学生经过收集挑选出如下几题：

1.如图1，△ABC 内接于⊙O，AH⊥BC 于点 H，若 AC=24，AH=18，⊙O的半径OC=13，则AB=______________。

2．如图2，E、F是正方形ABCD的边AD上有两个动点，满足AE=DF，连接CF交BD于G，连接BE交AG于点H，若正方形的边长为3，则线段DH长度的最小值是 。

3．如图3已知直线AB=8cm且端点A，B分别在x，y的正半轴上滑动，若∠OAB=20°，对应中点为M，当滑动到A1B1时，∠OB1A1=20°，对应中点M1，则中点M到M1的运动路径长为_____________。

图1

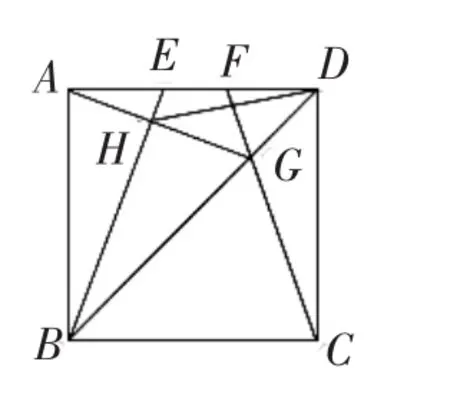
图2

图3

我将对学生的问题进行归类删选，上面仅仅给出的是三道题，班里面一共有十个小组，呈现给我的是30道题，我对这30道题进行修改删选，重点审核学生提供的题目是否真实反映了他们的薄弱环节，难度是否适中以及是否符合中考及课标的要求，审核通过后老师选取最有价值的几道题作为课堂例题（所谓有价值，主要考虑解题技巧是否多元化，可以更好地发挥学生发散思维，是否隐藏我们平时经常总结的一些解题思路、技巧和基本模型），当然老师在把关的过程中要权衡一章节的内容，考虑这三道题应有从不同解题方法，涵盖的不同的知识模块等。比如对上面三道题特点比较明显，首先对出题的学生加以肯定，但课堂上呈现的部分还必须由我加以修改，对于这里给出的第2题虽然是一道填空题，但是没有任何铺垫是无从下手的，因此我把这道题改成了一道简答题，分成两个小问题，降低难度。

如图4，E，F是正方形ABCD的边上两个动点，满足AE=DF，连接CF交BD于G，连接BE交AG于点H。

（1）求证：AG⊥BE；

（2）如图5，连接DH，若正方形的边长为4，则线段DH长度的最小值是_____________。

图4

可是这道题还是有一定的难度，我在前面加了一道预备题：

图6

图6 备用图

如图6，已知正方形ABCD的边长是4，点M是DC上的一个动点，连接AM，作BP⊥AM于点P，连接DP，在图6备用图中作出点P的路线，并求出当DP最小时DP的值。

学生在学习过程中经常会出现以前已经解决过的同类型的问题还是不会做，因此在教学过程中激发学生学习的积极性，提升他们的总结概括能力显得尤为重要。传统的教学学习知识是目的，通过问题引导，帮助掌握知识是手段；而现代学习中，学会寻找问题、发现问题、分析问题、解决问题才是真正学生学习成败的根本标准。因此在习题课中引导学生多思考解决问题的方法，总结解题思路，构建出一类问题的模型，形成建模思想是非常重要的。

二、顺学而导——习题课题目的讲解以学生为主

在讲解上面给出例题时，必须先给足学生思考时间，然后让学生上讲台来呈现解题思路以及思路产生的根由，接着由教师对学生呈现的思路进行一个补充，最后通过师生讨论总结出解题的基本模型。如上面呈现出来的四道题，我们可以归纳为三个类型，比如第一个例题我们可以看成是圆中出现线段垂直的问题，我们可以通过做直径构造相似三角形来解决；第二个例题可以看成是隐圆问题，出现一条定的边所对的动的角为固定值，那么这个角的顶点在一个圆上；第三个例题圆的概念问题，到定点距离等于定长，该点在圆上。

学生的思维是非常活跃的，他们所处的年龄正是表现欲望最强的时期，因此在课堂中鼓励学生多上台来展示自己的成果，对他们来说是一件非常快乐而又有意义的事情。

三、循学渐进——评价符合学生的个性化，作业制订遵循学生课堂掌握情况而定

对学生学习的评价应该体现学生个性化的需求，评价的标准很多，角度方法也很多，但以考试分数来决定学生学习的好与坏对学生是不公平的，也是片面的。我在评价过程中主要是以小组总分形式出现的，包含习题选取的打分（学生来操作），课堂参与度的打分（学生操作），查漏补缺打分以及最终的出测试卷和考测试分数（教师操作），以一定的占比相加，最终得出小组的总评分，整个班级被分成四个大组，大组之间进行评比，对于组评进行组内分析，在期中考试过后我们将进行一次颁奖，颁奖后将分数清零重新开始记分。这样更能激发学生的一种集体荣誉感，对于学习目标不明确的学生来说，这样的评价也能让他们产生更大的学习动力。

测试卷主要围绕我们的习题课内容展开，紧扣习题课的方法，题量不大，主要考查学生在习题课上讲评的知识点和解题方法。以下是我们本堂课的一份测试卷：

1．如图 7，∠MON=90°，矩形 ABCD 的顶点 A、B 分别在边OM，ON上，当B在边ON上运动时，A随之在边OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，求运动过程中，点D到点O的最大距离是_____________。

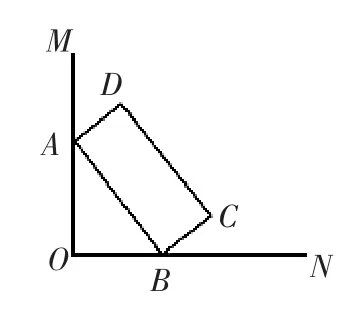
图7

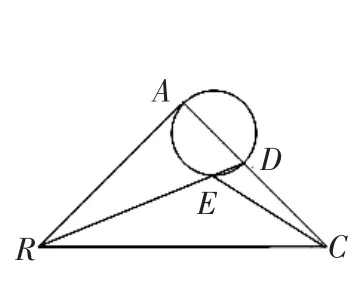
图8

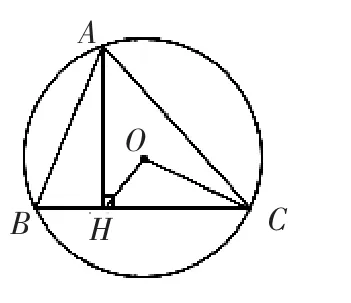
图9

2．如图 8，在等腰 Rt△ABC 中，∠BAC=90°，AB=AC，BC=4 姨 2，点D是AC边上一动点，连接BD，以AD为直径的圆交BD于点E，则线段CE长度的最小值是_____________。

3．如图 9，△ABC 内接于⊙O，AH⊥BC 于点 H，若 AC=8，AH=6，⊙O的半径OC=5，则AB的值为 （ ）

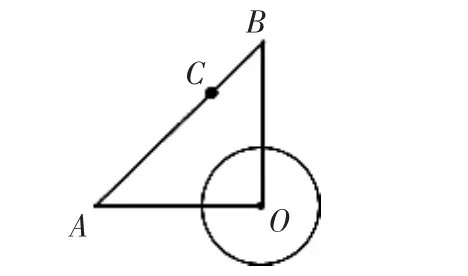
图10

5．如图 11，已知∠MON=30°，B 为 OM 上一点，BA⊥ON 于 A，四边形ABCD为正方形，P为射线BM上一动点，连接CP，将CP绕点C顺时针方向旋转90°得CE，连接BE，若则BE的最小值为_____________。

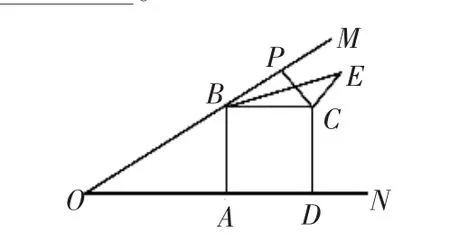
图11

新课程标准下的数学习题课教学方法是多种多样的，不管采用怎样的教学方法，我们都必须尊重学生的认知发展规律，以学生为主体，充分发挥学生的主动性、积极性，引导学生进行自主学习。但学生的自主学习缺乏方向性，因此教师的引导及对思想方法的归纳建立有效的解题模型也是不可缺少的。教师只有摆正“主”与“客”的位置，在教学中发挥积极的作用，才可以帮助学生尽快步入自主性学习的轨道，真正提高全体学生的科学素质。