在深度学习中发展数学核心素养——“圆的认识”教学片段与赏析

◇曾海燕

在一次教研活动中,山东省威海市名师陈梅老师执教了“圆的认识”一课。她的课堂以教师的深度教学，促进了学生深度地学习，从而发展学生的数学核心素养，这引起了笔者的强烈共鸣。

教学片段1

在画圆中认识圆的特征。

（学生尝试用圆规画2个、3个、4个圆后，师生交流学生的作品）

师：这两个圆画得似乎不太完美，（如图1）谁来说一说在画圆过程中，可能发生了什么？

图1

生：圆规的一脚偏了。

生：针尖移动了。

师：大家来看这3个圆，形状是一样的，但是大小一样吗？谁来说一说他是怎么画的，让这3个圆的大小不一样了？这3个圆的位置不同，他是怎么做到的？（如图2）

图2

生：圆规两脚间的距离不一样，圆规的脚的位置也不一样。

师：（出示同心圆，图略）再来看这2个圆，圆的大小变了吗？位置变没变？

生：大小变了，位置没变。

师：谁来总结一下，圆的大小是由谁来定的？圆的位置又是由谁来定的？也就是说，针尖的位置定了，两个针脚之间的距离定了，这个圆就定了，这两点是决定圆的两个关键因素。

师：既然这两点这么关键，我们就给它们专门起个名字：针尖定的位置称为圆心，用大写字母O表示;两个针脚叉开的距离称为半径，常用小写字母r表示。

师：中国人对起名字是有讲究的，你看我们把连接圆心和圆上任意一点的线段叫半径，半径，和“半”相对的，应该还有个“不半”，“全”径，数学上我们称为圆的直径。谁能来猜一猜什么样的线段是直径？用你自己的话来说一说。

生：两条半径合起来是直径。

师：还有其他表述方式吗？

……

师：我再画一条，这是直径吗？它和直径有什么区别？有什么相同的地方？两个端点都在圆上的线段称为弦。

师：大家继续思考，弦有多少条？为什么？它们的长度怎么样？为什么？最长的弦是什么呢？（生：就是直径，因为弦是两点都在圆上的线段嘛）一般的弦都比直径短，为什么呢？谁来说说道理？

（生答略）

师：大家的想象力都非常丰富，一下就想到弦的长度是怎么从小变大的，直到和直径一样长。那么，除想象之外，我们还有没有别的办法比较弦和直径的长短？比如，可以用什么工具？用尺子测量是种好办法，但它也有弊端，就是测量会有误差。能不能用推理的办法呢？这比较困难，我来帮大家一把，我把这两条半径画出来。

生：画出来后成了三角形，三角形两边之和大于第三边，而这两边的和就是直径，第三边就是弦，所以直径比一般的弦要长。

【赏析】本环节教师有的放矢地逐步呈现学生的作品，让学生通过观察、思考发现“圆的大小是由两个针脚张开的距离来定的，圆的位置又是由针尖定的位置来定的”，然后介绍圆心、半径。接着，引导学生探究半径、直径的特征……最后通过设置“半径（直径）都相等吗”“为什么相等”的问题，引导学生不满足于“动手”，而是积极地思考，从操作的角度上升到说理的角度，从具体形象思维过渡到抽象逻辑思维；通过设置“一般的弦都比直径要短，为什么”“谁来说说道理”，引导学生想象，再根据三角形两边之和大于第三边的推理，帮助学生的思维走向深入。

教学片段2

师：请大家翻开课前发的练习纸，在第一个图上，请你画一个圆。要求：这个圆的圆心是点C，点A和点B都在你画的这个圆上。（如图3）

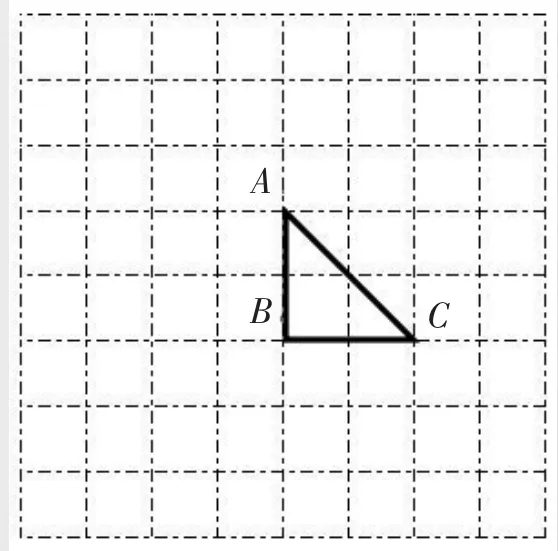
图3

师：遇到困难了吗？遇到困难别着急，我们反思一下，看看你遇到了什么困难。问题出在哪里？谁来说一说？AC的长度和BC的长度不相等，这个圆存在不存在？因此，我们动手之前，先要开动脑筋想一想。

师：第二个问题，还是请你画一个圆，要求：你先在A、B、C这三个点中选一个为圆心，其他两个点在圆上。

师：画完了吗？你选的以谁为圆心？点A和点C在圆上吗？为什么这次就能在圆上了？

【赏析】按要求画圆是对学生理解圆的本质特征“定点、定长”的进一步巩固，这里，表面上看是动手操作，实质上是引发学生的深度思考。