数形结合促进深度学习，有序思考提升想象能力——五年级“平面图形周长与面积”练习课教学实录与反思

◇钱金铎

一、注重对比，落实周长面积的“双基”要求

（呈现三道选择题）

1.图1中平行四边形的面积是（ ）平方厘米。

A.22 B.24 C.30

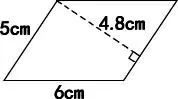
图1

2.在图2中，两条平行线之间三个图形（平行四边形ABFE、梯形BCMF和三角形DNM）的面积（ ）。

A.都不相等 B.有两个相等 C.都相等

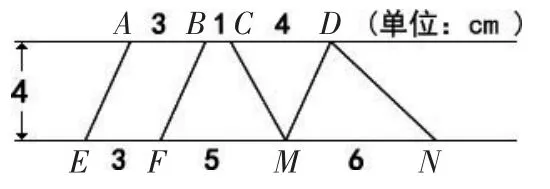
图2

3.如果图3中的平行四边形周长是60厘米，那么它的面积是（ ）平方厘米。

A.400 B.320 C.160

图3

（学生独立完成后同桌进行交流）

师：哪位同学想发表自己的选择结果和理由？

生：第1题我选C，理由是平行四边形的面积是底乘高；第2题也选择C，我用它们面积的计算公式计算过了，面积都是12平方厘米，所以都是相等的；第3题我选择B，先求出底：60-2×10=40（厘米），再求出它的面积：40×8=320（平方厘米）。

生：第1题选择C是错的，因为5厘米不是6厘米这条底上的高，应该选择B，应为5×4.8=24（平方厘米）。

师：你知道为什么要用底与它对应的高相乘才是它的面积吗？

生：因为把右上角一块割下拼到下面，就能变成一个长方形，这个长方形的长还是5厘米，宽就是原来平行四边形的高，长方形面积是长乘宽，所以结果应该是24平方厘米。

师：他讲的有没有道理？

生：有。

师：我们一起再来看看这位同学讲的思考过程（教师演示由平行四边形通过割补方法形成一个长方形的动态过程）。那么，为什么平行四边形的面积计算可以用长方形面积的计算方法来求得？

生：因为从平行四边形到长方形，虽然它们的形状改变了，但是面积没有变化。

师：说得很好！我们学习数学知识，不但要记得知识学习的结果，更应该理解和掌握这些知识的发生和发展过程。大家觉得第2道选择C有没有问题？

生：没有。

师：如果没有标明这组平行线之间的距离是4厘米，这个结论还正确吗？

生：还是正确的。因为这三个图形的高还都是一样的。如果用字母h表示高，那么它们的面积都是3h平方厘米。

师：说得多好呀！用字母能表示一个数，我们这位同学还能让它参加运算！

生：我觉得第3题选择B是错误的。

生：我也觉得是错误的。

师：还有哪些同学认为第3题选择B是错误的？

（大约有1半的学生举手）

师：我也认为选择B是错误的。现在同桌来交流一下为什么是错的。

（同桌之间交流分析）

生：要求这个平行四边形的面积，已经知道了有一条高是8厘米，现在要求出这条高下面的底，应该是用周长60厘米减去2个10厘米以后再除以2，等于20厘米，再计算20×8=160（平方厘米），那位同学忘记除以2了。

师：大家听懂了没有？

生：听懂了。

师：如果有同学选择A，他又错在什么地方呢？

生：我知道！他可能是用60-10后再乘8，就等于400平方厘米。也是把底算错了。

师：说得完全正确！同学们在解题时一定要仔细观察图形中的各种数据，并且做到合理运用。大家还有什么问题吗？

生：没有了。

师：你们没有，老师倒有一个问题呢！请大家仔细观察第2题中的图形。如果老师要求大家在这幅图中再画出面积和这几个一样的图形，比如平行四边形、三角形或者梯形，你能行吗？能画出多少个？现在同学们在四人小组里讨论交流你的想法，并把小组研究后发现的结论和理由告诉大家。

（学生分组研究）

生：老师，我们小组发现能画出平行四边形和三角形，而且能画无数个。

师：有理由吗？

生：只要把要画的平行四边形的一个底与原来平行四边形下面的底重合，上面的底与下面的底相等就可以了；三角形也是一样的，下底重合，顶点放到上面这条线上。

师：能否上来示范一下？

（学生上来比画，老师用课件协助。如图4）

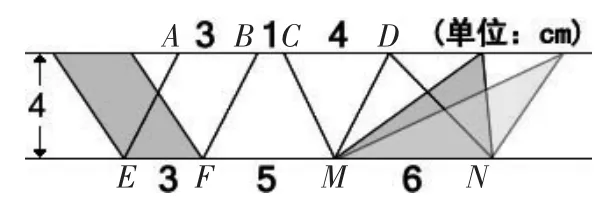
图4

生：梯形也是可以画的，只要上底是1厘米，下底是5厘米，高是4厘米的都可以。

生：不一定上底是1厘米，下底是5厘米，只要上底加下底的和是6厘米，高不变，面积就肯定相等。

师：你们太会动脑筋了！学习就应该这样，每天在原来理解的基础上再有所发现，如果还有创新就更好！

【反思】学生掌握数学知识，不能依赖死记硬背，而应以理解为基础，并在知识应用中不断巩固和深化。练习课尤其应该关注学生问题解决能力的有效提高，所以我们在教学中要注重数学知识的“生长点”与“延伸点”，将新授课中相对“碎片化”的数学知识有序有效地进行巩固和整合。以上三道选择题的正确选择，需要学生对图形的周长、面积概念和计算方法，以及计算公式的推导过程，周长、面积之间的关系有清晰的理解。在以上教学过程中，不但能让学生知道数学知识的发生和发展过程，而且通过追问的形式，激发学生进一步思考的兴趣——在学生完成正确选择后，老师及时引导：如果老师要求大家在这幅图中再画出面积和这几个一样的图形，比如平行四边形、三角形或者梯形，你能行吗？能画出多少个？这样做，使学生的思维跳出了原来的范围，为学生的多维想象和合理猜想创造了更大的空间，从而达到了进一步提高学生数学思维能力的效果。

二、数形结合，探索图形之间的内在联系

（出示：2个完全一样的等腰直角三角形）

师：请同学们仔细观察，你认为这是2个什么样的三角形？

生：是2个一样的直角三角形。

生：也可能是2个一样的等腰三角形。

师：如果这两位同学的猜想都是正确的话，那么应该是2个什么样的三角形？

（师将2个三角形重合一下）

生：2个完全一样的等腰直角三角形。

师：看着这2个完全一样的等腰直角三角形，你能联想到什么？

生：能拼成一个正方形，也能拼成一个大三角形。

生：还能拼成一个平行四边形。

师：这些图形都能拼成吗？

生：能，拼成的这些图形的面积是一样大的。因为它们都是这2个三角形拼成的。

（师板书：面积一样）

生：它们的周长有的一样长，有的不一样长。

师：具体说说。

生：拼成的大三角形和平行四边形的周长是一样长的，因为它们都是由原来三角形的2条直角边和2条斜边组成。但是正方形的周长要短一点，因为它是由4条直角边组成的。

师：如果我们用字母来帮忙的话，可以怎样来表示？大家先商量商量。

（同桌之间交流）

生：用a表示原来等腰直角三角形的一条直角边，用b表示一条斜边。那么，拼成的大三角形和平行四边形的周长是2a+2b，但是正方形周长是4a，所以要短一些。

师：大家已经理解了2个图形的拼组方法和结果。下面我们就来进一步研究4个完全一样的等腰直角三角形又能拼成哪些图形。看着这4个图形先请每位同学独立思考，进行合理的想象，猜想能拼成我们学过的哪些图形。要求是：先认真观察，然后进行动态想象、猜想判断，并把猜想判断的结果填写到表1中，最后是同桌操作验证。

4个完全一样的等腰直角三角形能够拼成下表中的什么图形？

表1

（生独立观察、思考、猜想、填写）

师：能猜想到的不一定会说得清楚，现在同桌先相互说说你猜想的过程和结果。

（生同桌交流）

师：你们认为哪个图形肯定是拼不成的？

生：圆。

师：说说你的理由。

……

师：其他的图形如长方形、正方形、三角形、平行四边形和梯形都能拼成吗？

（生出现不同意见）

师：大家有不同意见，我们可以拿出信封中的学具（4个完全一样的等腰直角三角形），同桌合作进行验证。

（生操作、验证。师有目的地让学生上台展示拼的过程，其中包括在拼成的平行四边形中，要求只移动一个小三角形就能变成一个大三角形或一个梯形……）

（师整体呈现拼成的不同图形。如图5）

图5

师：我们再来仔细观察这些拼成的5个不同图形，你们还能发现或提出什么数学问题？

生：我发现这些图形虽然形状不同，但是它们的面积相同。

师：为什么？

生：因为这些图形都是由4个一样大的三角形拼成的。

生：我想这些图形中，有的可能周长相同，有的可能周长不相同。

师：现在请大家再次进行小组合作研究，用什么样的办法能够有效地证明拼成的这些图形的面积一定相等，周长不一定相等？

（4人小组再次合作讨论）

生：我们先进行周长研究。可以用刚才研究2个三角形拼成图形的方法来进行。设每个等腰直角三角形的一条直角边为a，一条斜边为b，那么长方形的周长就是（2a+a）×2=6a，正方形周长是4b，平行四边形的周长是4a+2b，三角形的周长4a+2b，梯形的周长也是4a+2b，说明三角形、平行四边形和梯形的周长都一样长。长方形周长与这三个图形的周长肯定不一样长。

师：为什么？

生：因为6a可以看成是4a+2a，与4a+2b肯定不一样长。

师：那么正方形的周长4b怎么来解决呢？

生：4b也可以看成是2b+2b，但是比较难说清楚，反正已经有一样和不一样了。

师：是的，这一知识随着我们数学学习能力的不断提高，以后肯定可以解决的。

生：我们小组对拼成的5个图形面积进行了讨论，认为它们一定是相等的，因为这些图形的面积都是由4个完全一样的等腰直角三角形拼成的。

生：我们小组也用字母计算的方法对面积进行研究，知道了长方形的面积是：2a×a=2a2，正方形面积是b2，平行4边形面积也是2a×a=2a2，梯形面积是（a+3a）×a÷2=2a2，三角形面积是2a×2a÷2=2a2，说明4个图形的面积一样大，就是正方形面积b2不能证明与2a2一样大。

师：其他同学也真的没有办法说明了吗？难道一定要用b×b的方法来计算这个正方形的面积吗？

生：（思考后）我知道了——先看正方形中的一个大三角形，它的面积是2a×a÷2，那么2个大三角形拼成的正方形面积就是2a×a÷2×2=2a2！

【反思】以上的教学过程，不但让学生经历了2个完全一样的等腰直角三角形的简单观察、思考、交流和操作过程，而且重点让学生经历4个完全一样的等腰直角三角形拼组前的观察、想象和交流的思维过程。在这个过程中，引导者努力处理好“动手操作”与“动态想象”的辩证关系，让学生先独立思考、自主猜想，然后引导合作交流、操作验证。这样做，有利于学生在操作活动过程中进行数学化的思考，对想象活动进行必要的内化，也有利于学生空间观念的有效发展。在此基础上，再进一步运用数形结合的方法，将字母表示数应用到“图形与几何”的问题解答之中，有效地解决了“面积相等，周长不一定相等”的证明过程。