究竟如何塑造优质“数学文化课”

◇李铁安

《如何理解“数学文化课”的内涵与价值》［1］一文尝试性地阐释了：究竟什么是数学文化？数学究竟具有怎样的文化价值？究竟什么是数学文化课？在此基础上，本文进一步探析：优质的数学文化课究竟具有哪些基本特征？究竟如何塑造优质数学文化课？

一 优质“数学文化课”的基本特征

课堂教学是师生以人类优秀文化为中介的“教”与“学”相统一的教育实践活动，是学生的主观能动性与教师的主导作用以及教学内容的育人功能三个要素相互作用而形成的统一体。这是课堂教学的本质意义与内在逻辑。所谓优质课堂，应是学生主观能动性与教师主导作用以及教学内容育人功能得以最大限度地释放并尽可能达成和谐统一的课堂。

优质数学文化课堂就意味着：“充分彰显数学文化价值、充分发挥数学育人力量”，从而最直接激活学生数学学习动力，强有力改善学生数学学习境遇，深层次提升学生数学素养，根本性落实数学课堂育人宗旨。基于此，优质数学文化课应具备以下特征：

1.课程内容充满文化意蕴。即：课程内容本身更为科学地融入数学的文化元素，更为深刻地反映数学的学科本质，更为全面地体现数学的核心素养，更为综合地融合学科之外的知识；课程内容结构以富于挑战性的、生动的、开放的、有趣的数学问题来贯穿，问题之间的架构符合数学学科的内在逻辑和学生数学学习的认知逻辑等。

2.教师教学充满文化意趣。即：教师始终围绕数学问题展开教学，并基于问题解决采取适切的教学方式；教师自觉关注全体学生，关注不同层次学生的学习状态；教师提出数学问题时，要充分尊重和鼓励学生，给予学生足够的思考、探究和交流时间；教师充分关注学生数学学习过程中出现的认知问题，给予有针对性的引导与指导，并善于将学生提出的问题转化生成为新的学习资源。

3.学生学习充满文化意境。即：学生对数学学习表现出积极浓厚的兴趣，对数学问题充满好奇和探究的欲望；学生认真倾听、积极应对教师提出的问题以及同伴对问题的回答与解释，积极思考，并善于表达自己的观点，善于与同伴进行交流研讨；学生善于独立地思考问题，善于用数学化的思维方式思考和解决问题，善于从不同的角度思考问题，能够提出新的问题和想法，善于不断的追问与反思；全体学生在整个学习过程中经历完整丰满的问题解决过程，对数学学习活动获得愉悦体验和充实收获。

二 优质“数学文化课”的实施策略

要塑造一节优质数学文化课，就是在数学课堂上要尽可能地达成：让课程内容充满文化意蕴，让教师教学充满文化意趣，让学生学习充满文化意境。这其中，课程内容文化意蕴和学生学习文化意境的达成取决于教师高质量的备课和上课。

1.深挖课程价值，优化教学结构——为学生提供精良的数学学习资源。深化课程价值是对数学教学内容进行“问题化”的过程，优化教学结构是对问题化的数学教学内容进行“逻辑化”的过程。具体体现在：首先，教师要精选具有文化特质的数学题材，抽取其中的育人要素；如果是常态数学课，要精心挖掘数学知识背后所蕴含的文化要素。其次，要精准解析课程内容的知识结构，将课程内容静态的结论性知识转化为动态的开放性问题。最后，要精巧搭建课程内容的问题结构，使问题之间的架构符合数学学科的内在逻辑和学生学习的认知逻辑。

问题结构实质上是由一个个问题按照逻辑顺序架构起来的，这便为学生提供了一个充满学习意义的有利资源和抓手。当学生依托这个资源和抓手开展数学学习时，将经历一个发现和提出问题、分析和解决问题的完整过程，而恰是在这样的学习过程中，数学学科核心素养的基本要素悄悄浸润其中，学生对数学学习的火热情感、积极态度和灵动思维得以生长和张扬。

2.活化教师主导，优化教学过程——让学生经历完整的数学学习过程。活化教师主导是精准而灵活把握好对教学内容、教学策略、教学节奏等的驾驭尺度，优化教学过程是精心而灵动处理好对学生学习方式、思维过程、情感体验等的调控艺术。具体体现在：学习的任务容量要适当——教师要基于课程内容的难易度和学生的认知能力，整体把握学习内容的取舍；学习的过程环节要适合——教师要让学生经历认识、理解、巩固、应用这一完整的学习过程；学习的节奏进程要适宜——教师要合理调控学生对课程核心内容与关键问题学习的力度与时长；学习的策略方式要适切——教师要基于具体问题科学地组织教学，让学生采取灵活有效的学习方式解决问题；学习的主体体验要适度——教师要充分关注和活化学生学习过程中的生成，让学生在深刻的感悟和思维体验中享受数学文化的浸润过程。

三 优质“数学文化课”的案例举隅

【案例1】“完全数”教学设计（片段）

在数学史上，完全数是一个饶有趣味的话题，如果将完全数的史料作为一个数学教学的故事提供给学生，相信对开阔学生数学视野、调动学生探究兴趣不无裨益。而如果对完全数的定义、完全数的数字特征、完全数的基本规律等内容做深入挖掘，进而科学精巧地设计问题，也许更能体现和实现完全数这一内容题材的文化价值和育人功能。

1.问题挖掘与提炼。

以下选取一段基于完全数史料的问题设计及其教学过程（问题后面括号里边的内容是根据教学实录概要提炼出来的问题解答）。

（1）让学生概括完全数的定义。

问题①：请找出一组自然数，填入下面框图中，使等式成立。要求在同一种形状的框图里填入相同的数，不同形状的框图里填入不同的数。（1＋2＋3=1×2×3）

问题②：1＋2＋3=1×2×3，这个等式很美妙吧。怎么想到1、2、3这三个数的呢？（三个数相加等于这三个数相乘，这确实很神奇！等式前面是相加，后面是相乘，所以数字应该很小才可以）

问题③：想一想，6的真因子有哪些？（6的真因子有1、2、3这三个数）

问题④：试一试，用语言概括6=1＋2＋3的意义。（6恰好是它的所有真因子之和）

问题⑤：找一找，在10以内，还有这样的数吗？（没有）在20以内呢？（没有）在30以内呢？（兴奋——找到了！28=1＋2＋4＋7＋14）

问题⑥：像6和28这样的数，在数学史上被称为完全数。请尝试概括一下完全数的定义。（在自然数中，如果一个数恰好等于它的所有真因子之和，则称该数为“完全数”）

（2）让学生猜想完全数的数字特征。

问题①：完全数由古希腊毕达哥拉斯学派最先发现并命名。据数学史料介绍，毕达哥拉斯学派发现了前四个完全数，依次是6、28、496、8128。由此，你是否发现完全数的数字有什么特征？猜一猜，第五个完全数会是什么样子？第六个完全数又会是什么样子？（完全数的末位数是6、8、6、8……这样循环出现的规律，而第几个完全数应该是几位数；猜想第五个完全数末位数字应该是6，是五位数；第六个完全数末位数字应该是8，是六位数）

问题②：事实上，第五个完全数的末位数字确实是6，但它不是五位数！（兴奋之后是疑惑和好奇）是33550336（大吃一惊）；第六个完全数末位数字不是8，也不是六位数！（疑惑；更为大吃一惊）是8589869056（惊讶，好奇）。第七个和第八个完全数依次是137438691328和2305843008139952128（依然惊讶，好奇）。那么对此有什么感想？（学生：看来猜想是不可靠的！教师：的确，猜想与合情推理的结果必须经过严格的事实检验和逻辑证明。但猜想与合情推理是数学创造的重要来源。在数学学习中，敢于并学会大胆猜想和合情推理是非常宝贵的）

（3）让学生发现探究完全数的奇妙规律。

问题①：第一个完全数6=1+2+3，说明6可以怎样表示？那么第二个完全数28也能类似地表示吗？如何表示？［经历思考、探究、交流等过程之后：6可以用从1开始的连续三个自然数之和表示；如果1+2+3+…+x=28，则x（x+1）=56，由于x是非零自然数，所以x=7，所以28=1+2+3+…+6+7］

问题②：如果第三个完全数496也能类似地表示，那么怎样求出它应该从1一直加到哪个数？最终究竟如何表示？［1+2+3+…+x=496，则x（x+1）=992，由于x是非零自然数，可通过验算得出x=31，所以496=1+2+3+…+30+31］

2.育人价值解析。

通过对完全数史料的深入挖掘，设计出让学生概括完全数的定义、猜想完全数的数字特征、发现探究完全数的奇妙规律等几个基本问题，这些问题的解决蕴含了抽象、转化、类比、归纳、演绎、方程等丰富的数学思想。无疑，学生经历这些问题的解决过程也是充分发展学生数学抽象、逻辑推理、数学建模、数学运算等核心素养的过程。不仅如此，在这一过程中通过教师不失时机地引导点拨，也可培育学生数学学习的好奇心、审美直觉、大胆想象力和创造力等核心能力，还可以让学生初步感受基本的数学观念，体会数学的审美意蕴，以及感悟数学发现与创造的方法论。

而在对三个问题的结构设计上，不难发现，支撑各个问题的子问题之间具有严谨精妙的内在逻辑，可以圆满地反映问题解决的整个过程，由此，也必然使学生对问题的解决能够经历一个完整的过程。显见，这样的问题结构设计及其解决必然可以充分发挥出数学的育人价值和育人力量。

【案例2】“九宫图中的数学奥秘”教学设计

1.内容背景概述。

九宫图是中华传统数学文化的经典内容。将这一题材作为教学内容，其核心问题实质就是：究竟如何将1～9这九个数字填到一个九宫图中（如图1），保证横行、纵列、对角线上的数字之和都等于15？

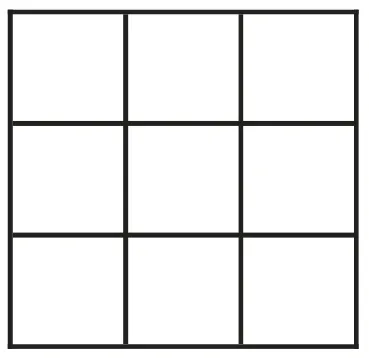
图1

如果把这个数学文化题材仅仅作为一个游戏提供给学生，不仅将本是一个奇妙的经典数学文化题材变得平淡无味、乏善可陈，也在很大程度上错失了一次让学生发现数学、热爱数学、欣赏数学和创造数学的良机。

2.教学过程设计。

如何把这个数学文化题材加工为学生学习的精良资源，从而尽可能让学生经历完整的数学学习过程呢？在小学的中、高学段，可做如下教学设计：

教师出示一个九宫格，让学生观察，之后提出问题：如何将1～9这九个数字填到一个九宫图中，保证横行、纵列、对角线上的数字之和都等于15呢？

教师提出要求：请同学们不要着急填数，独自认真地想一想，再试一试。

教师根据学生填图状况适当启发，自言自语地提示：你们在直觉上最先想到和尝试填哪一个格？（学生几乎会异口同声地说：中间格）这时教师鼓励并追问：这样想非常好！那么中间格究竟应该填哪个数呢？（一些学生会回答：中间格应该填数字5）这时教师再自言自语地提示：是填5吗？为什么呢？那就按照中间格填5，再尝试一下吧。（教师巡视学生填图情况，可选学生填错的和正确的结果在全班演示并检验正确与否）

教师提出新的问题：这个九宫图究竟应该怎样填数呢？让我们暂且放下这个问题，先探究一个很有意思的几何图形；请同学们认真观察这个米字格图形，如图2。

图2

教师追问：这个图形有什么特征？让学生独立思考，适时启发学生，最终让学生形成基本判断：是轴对称图形，有四条对称轴；也是中心对称图形，四条对称轴的交点是对称中心。

教师追问：这个图形有多少个交点？每个交点是怎样形成的？让学生独立思考，适时启发学生，最终让学生形成基本判断：一共有九个交点，中间的一点是四条线（四条对称轴）的交点；四个顶点分别是三条线（两条边、一条对角线）的交点；四个中点分别是两条线（一条边、一条对称轴）的交点。

教师继续提出问题：我们再回到问题本身，如果保证九宫图中横行、纵列、对角线上的数字之和都等于15，九宫格中的每一个格中的数字都分别参与了几次运算？请同学们认真观察独立思考，找到你的发现。最终让学生形成基本判断：中间方格上的数字参与4次运算；四个角方格上的数字参与3次运算；其余四个方格上的数字参与2次运算。

教师追问：谁能说一说这个问题与九宫图填数字有什么关系？让学生形成基本判断：米字格中的九个交点恰好可以对应九宫图中的九个格！

教师：非常好！那么我们接下来怎么办呢？让学生认识到：前面我们对九个交点进行了分类，相应地，按照数字奇偶性对1～9这九个数字分类。1、3、5、7、9是奇数，2、4、6、8是偶数。结合每个方格中的数字参与运算的次数，把数字5单独作为一类，它必然应该填到中间那个方格；然后1、3、7、9是一类，2、4、6、8又是一类，它们就应该分别填到四个顶角方格和其余四个方格中。

教师：真不错！那么再想一想，如果将1、3、7、9填在四个顶角方格中，相应地将2、4、6、8填在其余四个方格中，可以吗？如果不可以，应该如何填？为什么？你可以用哪个数学规律来解释？最终让学生形成基本判断：不可以。这样填，虽然可以保证中间行、中间列和两个对角线上的数字之和等于15，但两个边行和两个边列上的数字之和不能等于15。所以应在四个顶角方格上分别填数字2、4、6、8，相应地在其余四个方格上分别填数字1、3、7、9。因为15是奇数，而奇数+奇数+偶数=偶数，显然这不符合要求；但偶数+偶数+奇数=奇数，这就可以符合要求。

教师：我们可以看到，其实图形的对称性与数字的对称性在这里是和谐统一的。这就是九宫图在数学上的奥妙和迷人之处。

3.教育意蕴解析。

首先，教师提出问题：我们能否巧妙地填九宫图呢？这就把问题的解决直接交给学生了。其次，教师让学生先画出一个米字格图形，又一次提出问题：你能说出图形的对称性以及其中九个交点是怎么形成的吗？这样处理是为学生建立了一个熟悉的几何模型，让学生通过观察图形特征，获得审美直觉，并通过对交点进行分类，再联想九宫图中的数字分布规律要求，这就为有条理地对数字进行分类做了铺垫。

重要的是，在分析米字格中交点形成规律和九宫格中数字规律的过程中，渗透转化思想、类比思想、分类思想等。而在如何把1～9这九个数填入九宫格中的环节，通过对数字本身特征的分析，运用合情推理和演绎推理的思维方式，也同样渗透了丰富的数学思想并贯穿着演绎推理，这就使学生在解决问题的过程中经历了数学思想的熏陶和数学思维的训练。这样的教学设计，始终贯穿着问题解决，始终让学生自主地发现提出问题和分析解决问题。而学生在解决问题的过程中，无疑会感受数学的美丽和神奇。