数学课堂也须“回头看”

浙江省绍兴市上虞区沥海镇中学 范 青

数学的学习是一个由“不会到会”的转变过程，这种转变过程的媒介就是“问题”，问题是数学的心脏，是学生的思维中心．课堂教学中，教师应围绕教学内容，针对学生的知识和能力，设计诸多问题，并根据教学时机进行有效的课堂提问，引起学生对数学问题的思考，激发学生对问题的关注，调动学生的积极性，活跃课堂学习气氛．“设问惯性化”就是教师设计的“问题”要从学生的“最近发展区”出发，遵循学生的认知规律，问题小且具体，前后之间的联系要紧密，有梯度，形成一个问题链或问题串，学生在解决问题时，不需要在理解问题上花费大量的时间和精力．这样，不仅可以引导学生逐步深入的分析、解决问题，同时也达到加快课堂教学节奏的目的．

案例1：记得学校要我上一节公开课，我选择了浙教版八上“1．1．2认识三角形高线、中线、角平分线”，其中有一道例题.

原题：如图1-1，在△ABC中，AD是△ABC的高线，AE是△ABC的角平分线.已知∠B=75°，∠C=45°.求∠DAE 的大小.笔者随后设置了以下问题.

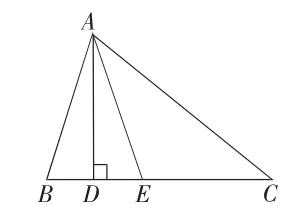
图1-1

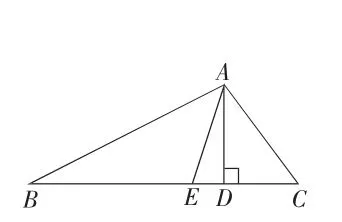
图1-2

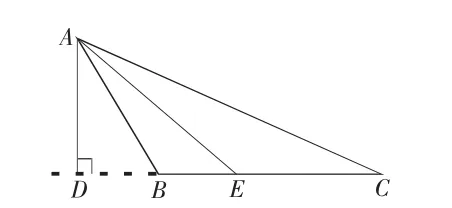
图1-3

问题 1：如图 1-2，若∠B=25°，∠C=55°.求∠DAE 的大小．

问题 2：如图 1-3，若∠B=115°，∠C=25°.求∠DAE 的大小．

问题3：从上述结论中，你认为∠DAE、∠ABC、∠C之间有何数量关系．

问题4：结合上述问题的解决若∠ABC=m，∠C=n，（m、n 满足三角形内角和的数量关系），则∠DAE的度数该如何表示．

学生经过认真分析讨论后发现：

① 若m=n时，高线AD和角平分线AE重合，此时∠DAE=（m-n）=0°；

② 若m＞n时，高线AD在角平分线AE左边，此时∠DAE=（n-m）；

③ 若m＜n时，高线AD在角平分线AE右边，此时∠DAE=（m-n）；

问题 5：如图 2-1，2-2，2-3，若点 A在角平分线AE所在的直线上移动到点F位置，作FD⊥BC于点D，∠DFE、∠B、∠C之间还有上述的数量关系吗？

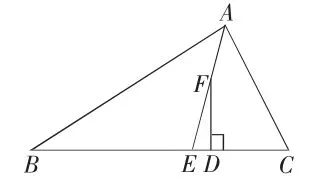
图2-1

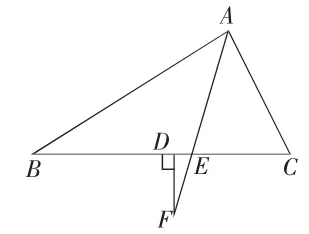
图2-2

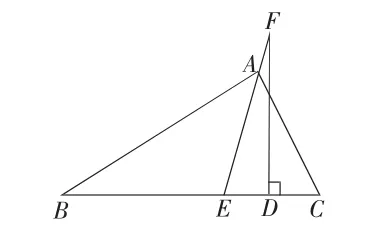
图2-3

案例2：九年级总复习设计的专题复习课“对角互补模型——全等形”摘取片段.

问题1：如图3-1，射线OC是∠BOA的平分线,PE⊥OB，PD⊥OA，在图形中你能得出哪些结论？

问题2：如图3-2，射线OC是∠BOA的平分线，∠PEO+∠PDO=180°，在图形中你能得出哪些结论？

问题 3：如图 3-3，已知∠BOA=90°，点P是∠BOA的平分线OC上的一点，∠EPD交 OA、OB 于点 D、E，且∠EPD=90°，图形中你还能得出哪些结论？

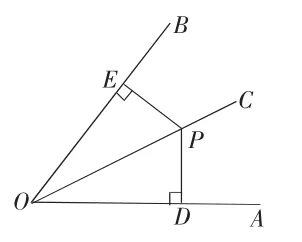
图3-1

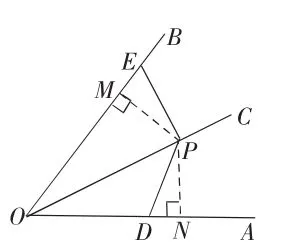
图3-2

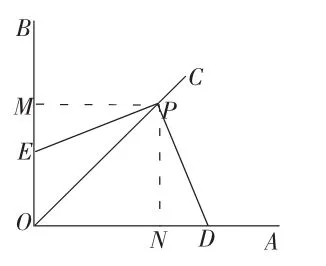
图3-3

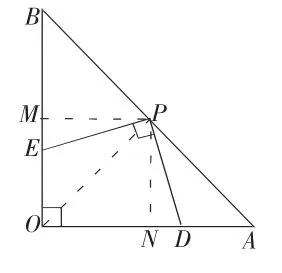
图3-4

问题4：如图3-4，在△AOB中，∠BOA=90°，AO=BO，P 为 AB 中点，∠EPD=90°，若AO=2．

①求OE+OD的值；

②判定四边形ODPE的面积是否会随着E、D的运动变化而变化，若变化试说明其变化范围；若不变，求出这个值．

问题5：在问题3的基础上，如图3-5那么当∠EPD绕点P旋转一定的角度后，上述结论还成立吗？

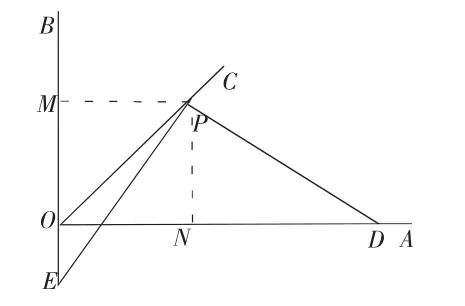
图3-5

评课时，教研组成员提出了很多宝贵的意见和建议，我在这里也把自己的感受表达出来与大家分享：

感悟1：学习过程比结果更重要

学习是一种过程而不是结果，新课程理念下的数学提倡的是：让学生经历观察、实验、猜想、证明等数学活动过程，因此，在课堂上学生的主体地位应得到最鲜明的体现。问题情景的设计，练习的安排等要尽可能地让所有学生都主动参与，提出各自解决问题的策略。教师应激发学生的学习积极性，向学生提供充分从事数学活动的机会，帮助他们在自主探索和合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想和方法，获得广泛的数学活动经验。

感悟2：大胆放手比直接授予更重要

孩子用自己的眼光看数学，教师应蹲下身子，和孩子站在同一视平线上，真正走入了孩子的心田，与孩子一起交流。不同的呈现方式，所产生的效果是截然不同的，四边形内角和定理的解释说明是本节课的重中之重，添加辅助线是关键，在教学过程中应该给学生充分的时间探索证明方法，让学生经历获得新知的成功体验。一个结论若由教师“给”学生只需要1分钟，而真正放手让学生自己去“取”的时间就可能是其数倍，甚至几十倍，虽然这样可能影响到一节课的教学任务，但是像这样放手让学生进行探索的机会还是不能轻易放过，学生们已经习惯了多思，什么事都要问个为什么，都要多找几条路走，面对这样的有主见、有创造性的学生，按部就班的授课早已满足不了他们了，这就要求作为新时代新课改中的教师不但要观念更新，在教学方法上不断更新、与时俱进，设计具有开放性的问题，给学生提供充分展示自己思维的空间，为学生个性思维的发展铺平道路，引领学生发散思维，培养创新意识，让学生得到全面的发展。

感悟3：及时总结比什么都重要

在二千多年前的《论语》中，曾子说过“一日三省吾身”的话语，阐明了自己立身处世的人生态度。“一日三省吾身”中“省”，是反思的意思。我想每位教师都会有这样的教学体验：教案初成，往往难以发现毛病；下课结束，教学设计的疏漏之处不找自现。再优秀的教师，再成功的教学，也难掩瑕疵。所以，教师必须对自己的课堂教学进行自我总结。自我总结既是教学过程的一个必要环节，是提高教学效益的重要途径，又是教师积累教学经验的有效方法。不断进行教学小结,可以获得宝贵的经验、教训，及时发现新问题，激发教师把教学实践提升到新的高度，实现教师的自我超越。

课堂教学的精彩常常不是(或者说基本上不是)因为老师的精彩而精彩，而是因为学生的精彩而精彩。好多情况下，掌声不是送给老师的，而是送给学生的。有时候你的课堂会有不少的“意外”，它其实都可以成为你以后教学和反思的最佳素材，教师要善于捕捉课堂互动过程中有价值的细节，不断反思，完善我们的数学课堂。不断的实践和思索使我渐渐明白，数学课堂，不但是要研究课本更得研究学生，教学是一门艺术，吾等虽非大师，却也须不断雕琢。

[1]伊红等.初中数学教学案例专题研究.浙江大学出版社.2005.

[2]胡兴余.中学数学教学思想与方法.上海社会科学院出版社，2007，104.

[3]张合远.精心设计问题串，提高教学有效性[J].中国数学教育，2010（7）17-20.

[4]陈建良.向来枉费推移力，此日中流自在行.2017.5.