基于高中数学教材旁白的微课教学实践研究

☉江苏省新海高级中学 顾秋婷

随着教育理念的不断更新，微课教学的优势已经受到越来越多教育者的认可，微课教育不光成为教育界关注的热点，更成为了社会关注的热点，但是经过查阅文献发现人们更多的是肯定微课教学的重要性，微课教学的实践却相对较少，因此，如何进行有效的微课教学设计成为了难点，另一方面，由于教材旁白（本文所指的教材旁白即指教材正文以外的课本上的内容，就苏教版而言，主要包括章头图、章引言、章首语、教材正文提示、链接拓展、课后阅读、实践操作及拓展探究等除教材正文以外的课本上的内容）内容精简，信息量大，指向性强，而在日常教学中教师可能会因为课时紧张等原因忽视教材旁白的教学，因此教材旁白特别适合微课教学，所以本文将开展基于教材旁白的微课教学实践研究.

一、教材旁白的微课教学价值

1.直观易懂，让数学更贴近生活

教材很多时候会将一章节的“魂”蕴含在形象直观的章头图或是富有哲理的章首语和章引言中，利用这些教材旁白进行微课教学能帮助学生对抽象知识的理解，减轻学生对数学的畏惧心理.例如，苏教版选修1-2第一章《导数及其应用》的过山车章头图，如图1，在过山车的上升和下降中体现函数的单调性，过山车的每个时刻的方向又是函数在每一点导数的生活载体，如果利用这幅章头图进行导数与函数单调性的研究不光能让学生找到数学的生活模型，更能让学生通过坐过山车的感受去理解二者的密切关系，有助于突破本节课的重难点.

图1

2.诠释概念，深入核心知识理解

教材中的正文提示和课后探究是对该节内容知识的点拨、扩充、拓展、深化和升华，正文旁白和课后探究的理解程度从一定意义上将决定本节内容的掌握程度，因此这些教材旁白的重要性不言而喻.但在实际教学中，有些“过简单”或是“不会考”的教材旁白就会被忽视掉，而这些容易被忽视的教材旁白可能恰恰是学生的薄弱点或易错点，如果不能正确对待这些教材旁白将会使学生的核心概念理解大打折扣.例如，选修2-1（或选修1-1）《圆锥曲线》这一章节的折纸探究题，如图2，许多教师在教学中会无视它的存在，而这个折纸游戏恰恰能帮助学生更深入地理解圆锥曲线的概念和性质.

图2

3.开拓眼界，提高学生核心素养

教材在许多章节后都配有课后阅读或是相关知识链接等教材旁白，这些教材旁白都在讲述着知识背后的故事，如果教师能够在学习新知识的同时和学生一起去研究知识产生的背景，让学生感觉到这些知识是实实在在的活着，并联系着我们生活中的过去、现在和未来.例如，《数列》的课后阅读——斐波那契数列，如图3，它和兔子繁殖、树干生长等生活场景是息息相关的，学生一方面可以结合数列的知识用数学的眼光去观察世界，了解世界，另一方面也可以通过熟悉的生活常识去学习数学，理解数学，进而掌握数学知识.

图3

二、基于教材旁白的微课教学实践

基于教材旁白的微课教学有诸多的实际意义，那么究竟该如何进行设计和实践微课教学呢？下面本文以问题探究教材旁白中的《纸折圆锥曲线》（该微课在省首届微课大赛中获得了一等奖）的微课教学为例来进行教材旁白微课教学设计与实践，与同行共勉！

教学过程：

2.常春藤 是室内常见的垂吊盆栽，它叶片上的微小气孔能吸收空气中的烟雾、尼古丁和甲醛，并将其转化成无害的糖和氨基酸，能够有效抑制尼古丁中致癌物质的产生。常春藤的茎蔓非常容易生根，通常采用扦插的方式繁殖。同时，常春藤不喜阳光，一定要放在通风凉爽处养护。

1.巧妙铺设，激发兴趣

同学们经常做物理、化学、生物实验，可是你们做过数学实验吗？荷兰数学家弗赖登塔尔曾经反复强调：“学习数学的唯一正确的方法就是实行‘再创造’，而游戏是同学们获得数学内容与思想的有效方法之一.所以本节课我们就一起利用折纸游戏去进一步探究圆锥曲线的定义及其内涵.

设计意图：通过学生熟悉的物化生实验及游戏入手激发学生的学习兴趣，为下文的研究埋下伏笔.

请同学们准备一张印有定圆O的圆形纸片，按照以下步骤操作：在圆内任取不同于圆心F1的一点F2（如图4），将纸片折起，使圆周过点F2，然后将纸片展开，就得到一条折痕（为了看清楚，可把直线l画出来）.这样继续折下去就可以画出一系列折痕，这些折痕将衬托出一个非常漂亮的图形，大家想知道是什么图形吗？接下来请同学们自己动手折一折，画出折痕，看谁画的又快又好.

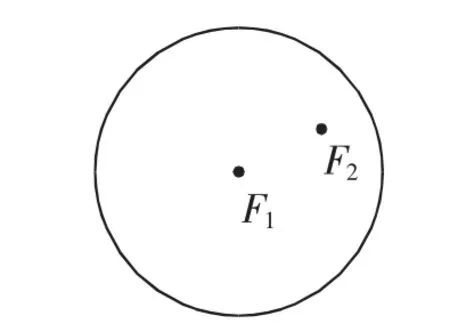
图4

【播放折纸示范视频】

设计意图：对于很多学生而言，数学是枯燥的、严谨的，这样设计更容易激起学生的学习激情与求知欲.

2.故设悬疑，探索新知

相信同学们经过几次对折后会得到图5的图形，随着对折次数的增多会形成图6的图形，你能看出来这些折痕衬托的是什么图形吗？是的，当对折次数越来越多时，折纸所形成的图形就越来越接近椭圆.但手工制作的图不够精确，只有取遍圆周上的所有点才会非常精确.但是要想取遍圆周上所有的点，这个工作量非常大，接下来我们就借助“几何画板”工具，让电脑来帮助我们演示作图.

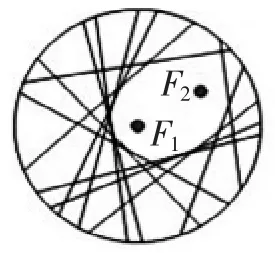
图5

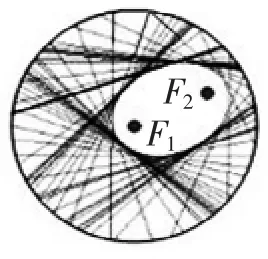
图6

肯定有同学会有以下的疑惑：

问题1：为什么衬托出的中间的空白部分恰好是一个椭圆呢？究竟是什么原因造成了这样的结果？

为了解决这个问题，我们不妨研究其中的一条折痕l.过F2作l的垂线交圆于Q，折痕l是线段F2Q的垂直平分线.连接F1F2，交l于P点，连接PF2，则PF1+PF2=PF1+PQ=F1Q=R＞F1F2，故P在以F1，F2为焦点的椭圆上.

问题2：折痕l上除了P点在该椭圆上，还有其他点吗？

我们不妨在此折痕l上除点P外任取一点M，在l上另取不同于P的任意一点M，可知MF1+MF2=MF1+MQ＞F1Q=R.故M在椭圆外部，即折痕l上只有点P满足条件.P是l与椭圆的唯一公共点，折痕其实是该空白部分椭圆的一条切线，同理，每一条折痕都是该椭圆的切线，这无数条切线包围住椭圆，也就衬托出了椭圆的轮廓，这就是我们用折纸法折出椭圆的原理所在.

设计意图：从为什么是椭圆、折痕上有几个点在椭圆上两方面探索知识更易让学生理解椭圆的生成过程与内涵.

3.柳暗花明，引入新知

我们把在平面内，与两个定点F1、F2的距离之和是一个常数（大于F1F2）的点的轨迹叫椭圆.

4.峰回路转，顺流而下

前面我们通过折纸了解了椭圆的形成过程及其原理，下面我们继续通过折纸来探究其他的曲线：在纸上画一个圆，在圆外任取一定点F，将纸片折起，使圆周过点F，然后将纸片展开，就得到一条折痕（为了看清楚，可把直线l画出来）.这样继续折下去，得到若干条折痕.观察这些折痕围成的轮廓，它是什么曲线？

类比椭圆定义的推导过程，请同学们带着下面一系列问题自主探究：

问题1：折痕围成的图形是什么？你能证明吗？

问题2：类比椭圆的定义，你能否尝试着概括一下双曲线的定义？

问题3：你能说说椭圆定义与双曲线定义的区别吗？

设计意图：双曲线与椭圆有许多相似的性质，学生可通过类比椭圆的形成过程及其原理得出双曲线的概念，符合学生的认知规律.

新课标的教材编写特别注重知识的系统性，对于抛物线的教学引入也可以用折纸的背景.类比前面椭圆和双曲线的推导过程，请同学们课后独立完成.

设计意图：椭圆、双曲线及抛物线统称为圆锥曲线，为体现知识的系统性，且又不嫌罗嗦，特将抛物线的形成过程作为学生课后探究.

结合上述分析，我们相信基于教材旁白的微课教学作为一个新兴事物有着它独特的魅力和优势，它能深入挖掘教材旁白的涵义，使得教材更好地运用于教学中，从而帮助教师提高教学质量，促进学生更深入地理解和掌握所学知识，所以基于教材旁白的微课教学是大势所趋，人心所向，期待并憧憬着这一天快点到来！

1.胡铁生.“微课”：区域教育信发展的新趋势［J］.电化教育研究，2011（10）.

2.苏小兵，管珏琪，钱冬明，祝智庭.微课概念辨析及其教学应用研究［J］.电化教育研究，2014（07）.

3.张一川，钱扬义.国内外“微课”资源建设与应用进展［J］.远程教育杂志，2013（6）.

4.梁乐明，曹俏俏，张宝辉.微课程设计模式研究——基于国内外微课程的对比分析［J］.开放教育研究，2013（2）.

5.董入兴.对苏教版高中数学教材旁白的几点认识［J］.中学数学参考，2008（4）.F