多道瞬变电磁法中m序列抗噪性定量评估及编码参数优选

袁 哲 张一鸣 郑起佳

(北京工业大学,北京 100124)

1 引言

大地可等效为线性时不变系统，因此其电磁冲激响应理论上包含全部地电信息。在人工源电磁探测中，通过观测人工场源激励下的大地电磁响应信号，构造大地系统的输入、输出模型，可实现大地电磁冲激响应的辨识，即大地的“全系统观测”。

从系统辨识的角度看，发射源作为辨识过程的输入信号，应保证能够持续激励被辨识系统的所有模态，即激励源带宽相对于观测系统带宽要足够大，才能保证辨识的质量与精度。m序列具有频带宽、谱密度高、白噪声特性好的优点，可以满足以上要求，成为人工源电磁探测领域中的研究热点。

Quincy等[1]首次将m序列应用到瞬变电磁法中； 之后Duncan等[2]采用长线源进行m序列编码发射，对埋深为500m的目标体进行了探测； Wright等[3]将m序列应用到多道瞬变电磁法，并采用拟地震方法对资料进行解释； Ziolkowski等[4,5]先后在陆地及海洋成功地实施了MTEM验证试验； 赵碧如等[6]研制了基于伪随机码发射源的PS100型激电法电测仪系统，并开展了野外实测； 王忠仁等[7]利用三元伪随机序列进行可控震源信号编码设计，抑制了响应剖面中的相干噪声； 汤井田等[8]完成了基于逆重复m序列伪随机电磁法的相关研究，讨论了编码电磁测深原理及参数提取方法； 王显祥等[9]通过数值模拟分析了m序列激励源对高阻体的探测效果。

在m序列的抗噪性能方面，Helwig等[10]使用m序列替代阶跃信号作为长偏移距瞬变电磁测深法(LOTEM)的激励源，取得了明显的信噪比增益；罗维斌等[11]采用逆重复m序列作为激励源，通过收—发相关运算实现地电断面的精细探测，研究结果表明采用逆重复m序列作为激励源可极大地压制干扰； Ziolkowski[12]通过相关运算分离并评估响应信号中的估计噪声与环境噪声，实现对辨识效果的量化评估； Ilyichev等[13]从数值模拟和野外试验两方面研究了m序列的抗噪能力，研究表明m序列的抗噪能力相对于传统方法可使信噪比提高100倍左右。

在m序列编码参数优选方面，由于m序列具备多个编码参数，编码参数的不同组合直接影响其抗噪性能。前人总结了部分参数的抗噪规律，Ziol-kowski[14]指出提高m序列阶数能够改善大地电磁冲激响应的辨识精度； 武欣等[15]提出一种改进的大地冲激响应的数学方法，同时对以m序列为发射波形的勘探系统相关参数选择进行了分析； 王显祥等[16]指出编码参数应结合环境噪声进行调整。但目前仍无法定量评估不同编码参数m序列的抗噪性能，相应的优选方案尚待研究。

本文在前人研究的基础上，基于多道瞬变电磁法的工作原理，首先回顾了大地电磁冲激响应的辨识方法，并分析m序列的频谱特征； 随后对比了不同编码参数m序列的辨识效果，通过将辨识过程等效为辨识系统，分析特定频点处的辨识系统频响特性，实现不同编码参数m序列抗噪性能的定量评估； 在此基础上，通过数值模拟分析各编码参数对抗噪性能的影响，进而给出m序列编码参数的优选方案； 最后野外试验数据处理结果验证了本文所述编码参数优选方案的可行性。

2 大地电磁冲激响应辨识

大地电磁冲激响应的辨识采用类地震的方法[17,18]，工作原理见图1。该系统通过发射电极A、B发送m序列编码电流信号对大地进行激励，作为大地系统的输入信号。在发射电极轴向延长线上布置接收阵列，同步观测大地远端的时变响应电压，作为大地系统的输出信号，将大地等效为线性时不变系统,其输出信号(图1)可表示为

r(t)=g(t)*s(t)+u(t)

(1)

式中：r(t)为接收到的远端响应电压信号；g(t)为待辨识的大地电磁冲激响应；s(t)为发射电流信号；u(t)为噪声信号，包含人文噪声和随机噪声。

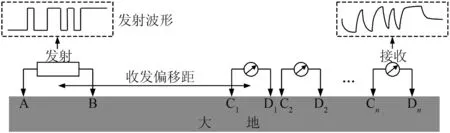
图1 大地电磁冲激响应辨识原理

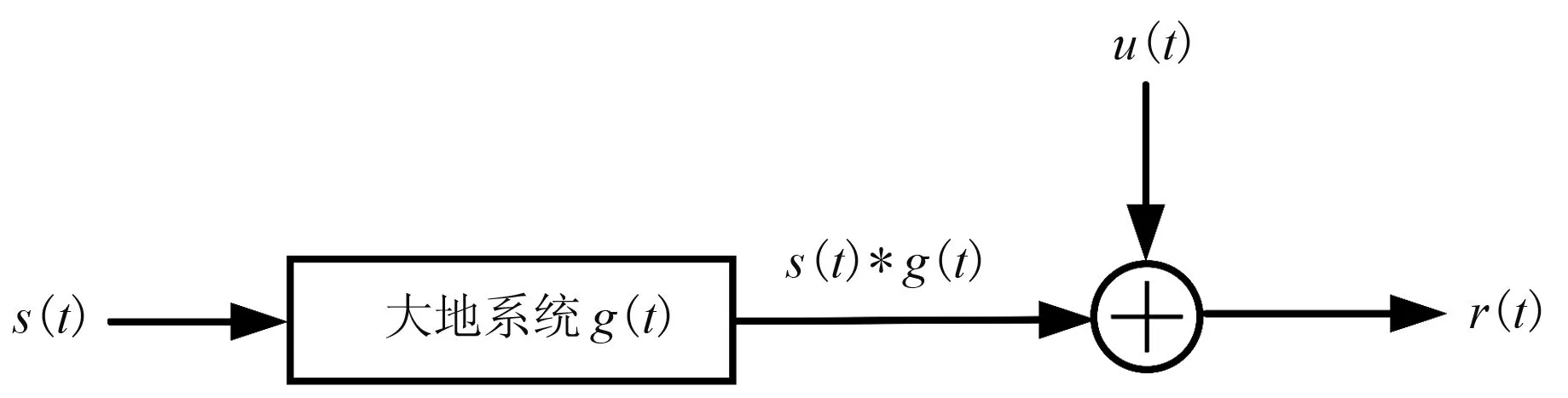
图2 大地褶积模型

利用反褶积可从发射电流s(t)与响应电压r(t)中恢复大地电磁冲激响应，即构建一反算子b(t)，使其满足

b(t)*s(t)=δ(t)

(2)

式中δ(t)为单位冲激信号。反算子b(t)可通过维纳反褶积求取，其推导过程见附录A。

式(1)两边同时褶积b(t)， 可实现大地冲激响应的辨识

r(t)*b(t) =g(t)*s(t)*b(t)+u(t)*b(t)

=g(t)+u(t)*b(t)

(3)

显然式(3)所述辨识结果包含噪声分量u(t)*b(t)。定义辨识信噪比Ridt以表征辨识精度

(4)

将大地等效为时不变系统，即g(t)恒稳不变。为获得较高的辨识信噪比，应保证式(4)的分母u(t)*b(t)尽可能地小，即辨识过程应具备较强的噪声压制能力。

3 m序列

一个序列如果既可以被预先确定、重复和复制，又具有白噪声序列所具有的统计特性，那么称这种序列为伪随机序列。m序列是最长线性反馈移位寄存器序列的简称，其实现简单、理论成熟，是一种应用广泛的伪随机序列[19]。

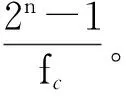
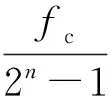
图3 5阶m序列编码示意图

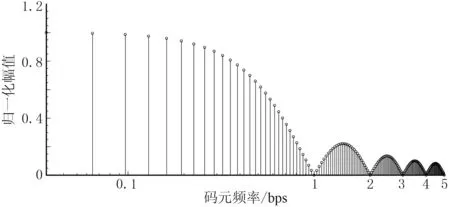
图4 5阶m序列频谱

4 不同编码参数m序列的辨识效果

产生一组m序列需要确定四个编码参数：本原多项式、初始状态、阶数以及码元频率。由于本原多项式与初始状态不会改变m序列的频谱特性，因此进行大地电磁冲激响应的辨识时，一般只调整m序列的阶数以及码元频率。

为了研究不同编码参数下大地电磁冲激响应的辨识效果，以均匀半空间模型为例进行说明。电阻率为ρ的均匀半空间的轴向响应电场E(t)可通过下式求取[21]

(5)

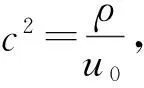
(6)

结合式(1)可得到均匀半空间的远端响应电压信号r(t)，在此基础上可利用式(3)求得均匀半空间电磁冲激响应的辨识解。为与解析解区分，用gi(t)表示辨识解。显然，辨识解与解析解的吻合程度正比于辨识精度，因此可用辨识误差率Rerr表征这种吻合程度

(7)

通过绘制辨识误差率曲线，可分析大地电磁冲激响应的辨识解在各时段与解析解的吻合程度。

4.1 无噪声环境下不同编码参数m序列的辨识效果

首先考虑无噪声环境下不同的编码参数组合对大地电磁冲激响应辨识的影响，均匀半空间模型参数见表1。

随机选用三组不同编码参数的单周期m序列对上述模型的电磁冲激响应进行辨识，编码参数见表2。

表1 均匀半空间模型计算参数

表2 三组编码参数

图5为三组编码参数下的发射电流波形以及响应电压波形。其中图5a～图5c为对应的三组发射电流波形，其时间长度随着阶数与码元频率的不同组合而变化； 图5d～图5f为对应的三组响应电压波形。

图6a为三组收发波形对应的电磁冲激响应辨识结果，可以看出在无噪声环境下，使用不同编码参数m序列得到的电磁冲激响应辨识解均能与解析解很好地吻合。图6b表明三组辨识解的辨识误差率均小于2%，早期趋势的辨识误差率均稳定在1%以内，即在无噪声环境下使用不同编码参数的m序列作为激励源均能取得较好的辨识效果。

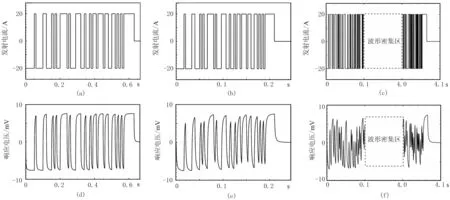
图5 无噪声环境下三组编码参数对应的收/发波形 (a)第一组编码发射电流波形； (b)第二组编码发射电流波形； (c)第三组编码发射电流波形(0～0.1s和4.0～4.1s波形放大显示)； (d)第 一组编码的响应电压波形； (e)第二组编码的响应电压波形； (f)第三组编码的响应电压波形(0～0.1s和4.0～4.1s波形放大显示)

4.2 噪声环境下不同编码参数m序列的辨识效果

考虑含噪声环境，沿用表1和表2的各项参数，并在响应电压信号中引入振幅为5mV的50Hz干扰信号，图7为该噪声环境下三组编码参数对应的接收波形。

图8a为噪声环境下，三组m序列对应的电磁脉冲响应辨识解，其中第三组的辨识解与解析解较吻合，另外两组则能观察到明显的50Hz噪声扰动。图8b表明第三组的辨识误差率控制在1%以内，而另外两组的辨识误差率较大，第一组在晚期甚至超过15%。可见在噪声环境下，不同编码参数的m序列具有不同的抗噪性能。因此，编码参数的优化选择成为大地电磁冲激响应高精度辨识的重要环节。为此需要深入研究m序列的抗噪机制，对不同编码参数m序列的抗噪性能进行定量评估，进而给出m序列编码参数的优选方案。

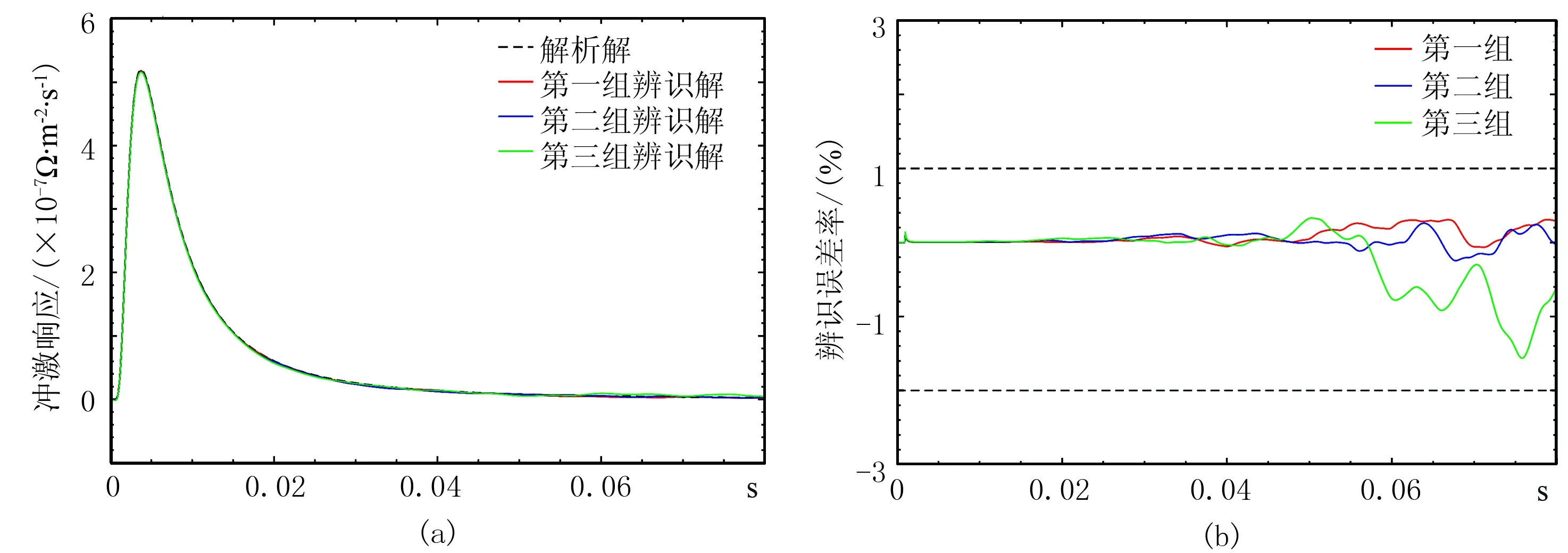
图6 无噪声环境下三组编码参数对应的辨识结果(a)及辨识误差率(b)

图7 噪声环境下三组编码参数对应的响应电压波形 (a)第一组编码； (b)第二组编码； (c)第三组编码(0～0.1s和4.0～4.1s波形放大显示)

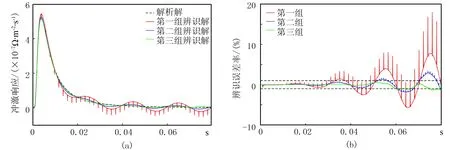
图8 噪声环境下三组编码参数对应的辨识结果(a)及辨识误差率(b)

5 辨识系统

工程中通常使用两种数学模型表征一个系统：冲激响应与频率响应。二者可在时间—频率域中相互转换。对应不同的数学模型，系统的输出可表示为输入信号与冲激响应的时域卷积或与频率响应的频域之乘积。式(3)表明辨识过程的本质是构建一辨识系统。反算子b(t)为该系统的冲激响应，具体可分为两部分：包含大地电磁冲激响应的有用信号分量

以及噪声分量

噪声u(t)中包含随机噪声与人文噪声，后者主要是指人文活动带来的电磁干扰，例如电力传输线引入的工频干扰，这些噪声一般包含特定的频点，例如50Hz基频及其奇次谐频。与随机噪声相比，人文噪声干扰强度大，频点分布集中，是主要干扰源。因此，通过分析辨识系统在噪声频点处的频响特性B(ω)，能够实现辨识过程抗噪性能的定量评估，其中ω为角频率。B(ω)可由b(t)通过傅里叶变换得到。由于噪声分量一般只考虑幅值压制，而不考虑相位畸变，因此需重点关注辨识系统的幅频响应|B(ω)|。

6 数值模拟

6.1 阶数

沿用表1均匀半空间模型，分别使用4～12阶m序列作为激励源，码元频率均为2kbps，噪声环境为幅值5mV的50Hz干扰。图11为各阶辨识系统在0～6000Hz以及40～60Hz频带的幅频响应。

从图11a可以看出各阶辨识系统的幅频响应在整个频带范围内均有较大的衰减值(均大于60dB)，保证了辨识过程对噪声的基本压制作用；各阶辨识系统的幅频响应在2000、4000、6000Hz频点附近有明显上升，并在这些频点取得极大值，表明辨识系统对码元频率及其谐频处噪声的压制能力较弱。为论述方便，称此类频点为敏感频点，该类频点会导致辨识解中出现同频干扰(在后文将有详细论述)。此外，图11a中各幅频响应存在明显的分层现象，即各幅频响应的衰减值随着阶数增加而增加，因此使用高阶m序列能够获得更好的噪声压制效果。

图11b为40～60Hz频带内的频响特性。以50Hz工频干扰频点为例，每提高一阶噪声衰减可增加5～10dB(图12a)。下面以4、8、12阶m序列对应的辨识解进行说明。由图12b可见，使用12阶m序列得到的辨识解与解析解吻合度最高，使用4阶m序列得到的辨识解失真最严重。由图12c可见，使用4阶m序列的辨识误差率超过了10%，8阶m序列对应误差率有所降低，12阶m序列对应的辨识误差率最低(1%以内)，具有较高的辨识精度。另外，4、8阶对应的辨识误差曲线中存在明显的高频扰动，这是前文在图11a中提及的敏感频点所致。使用式(4)计算各阶辨识信噪比，结果见图12d，可以看出每增加1阶可以带来2～7dB的辨识信噪比增益。

6.2 码元频率

据趋肤深度公式，发射源的频点分布与探测深度总体呈“高频测浅，低频测深”的关系[22]。图13a为传统方波激励源在1000Hz和1500Hz发射频率下的频谱图，可见方波激励源仅包含基频和奇次谐频，单频发射时频点集中，探测深度直接受限于发射频率，因此通常需要进行扫频发射(例如CSAMT)。与方波激励源不同，m序列激励源的频带较宽，频点丰富。图13b为码元频率分别取1500bps和2000bps时m序列的频谱图，可见码元频率的增加只会导致谱能量的转移(从低频段转移至高频段)，而不会改变频点分布。因此对于m序列激励源，码元频率受趋肤深度影响较小，因此在野外施工时只能确定码元频率的大概区间，具有一定的“盲目性”与“试探性”。本文从辨识系统的角度对不同码元频率的辨识效果进行分析，继而得出码元频率的优选方案。

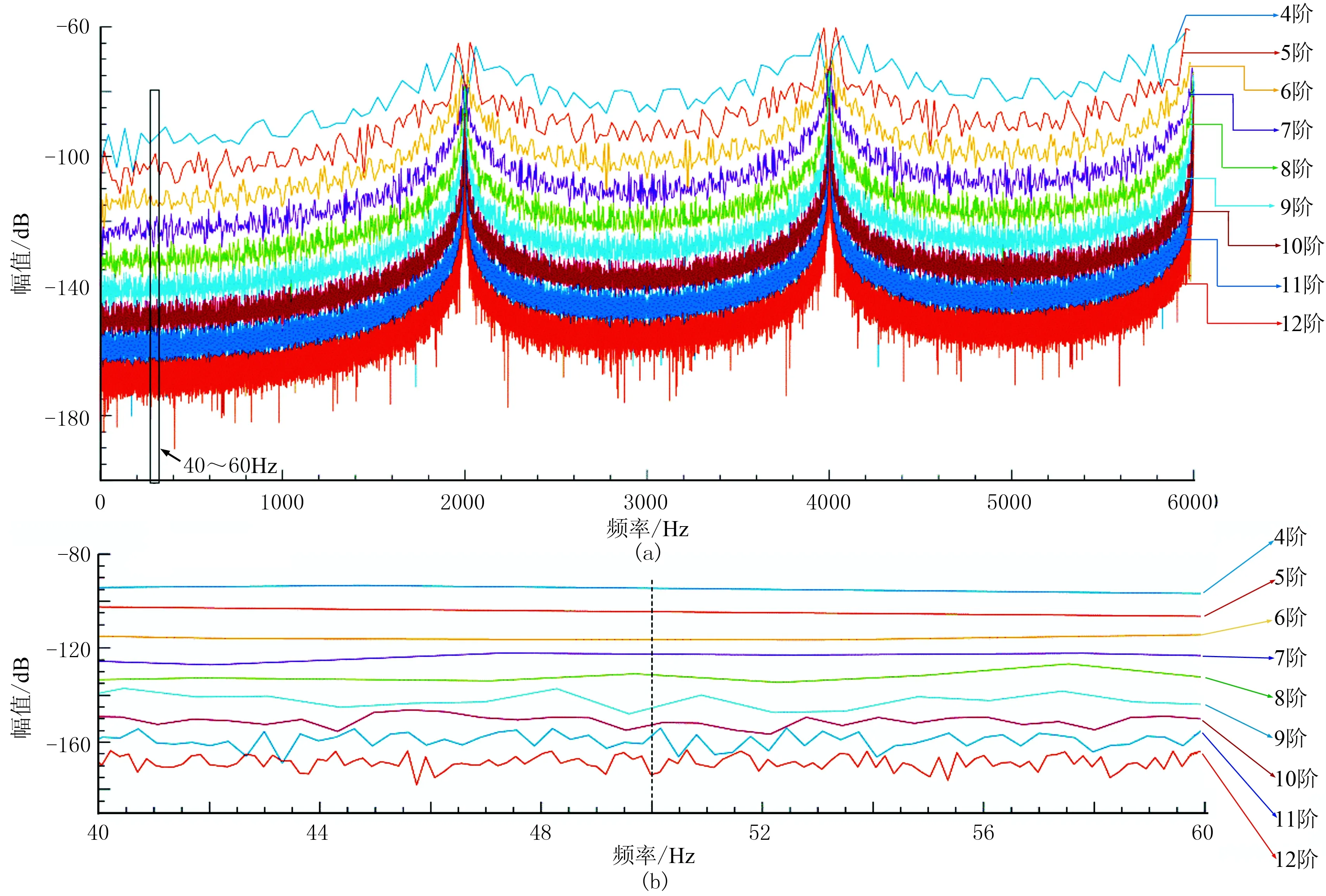
图11 各阶辨识系统的幅频响应 (a)0～6000Hz； (b)40～60Hz

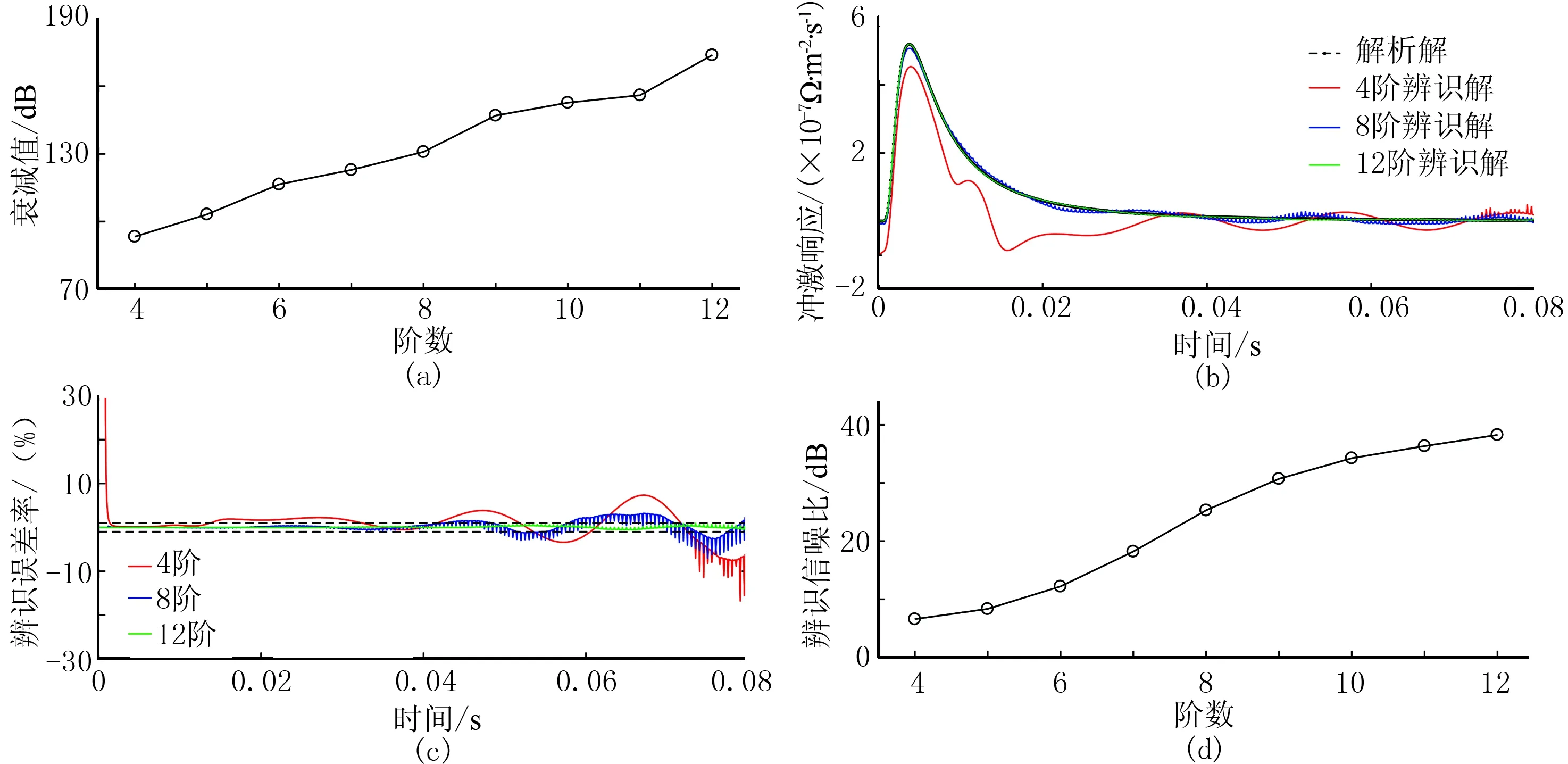
图12 不同阶数m序列的辨识效果 (a)4～12阶辨识系统在50Hz处的频响衰减值； (b)4、8、12阶m序列所对应的大地电磁冲激响应辨识解； (c)4、8、12阶m序列所对应的辨识误差率曲线； (d)4～12阶m序列对应的辨识信噪比

沿用上节模型，采样率改为14322Hz，采用10阶m序列作为发射源，分别以六组码元频率进行编码： 256、512、1024、1792、3584、7168bps。图14为六组码元频率对应的辨识系统在0～7166Hz以及40～60Hz频带的幅频响应。类似于图11，每组幅频响应均在码元频率及其谐频处取得极大值，从而导致辨识解中存在高频干扰(图15c)。很显然较低的码元频率具有更多的敏感频点，增加了后期滤除高频干扰的难度。另一方面，随着码元频率的增加，辨识系统幅频响应的衰减值逐渐降低。以50Hz频点为例，码元频率每增加512bps，相应的辨识系统幅频响应衰减值降低8～10dB(图15a)，说明增加码元频率会削弱辨识过程的噪声压制能力。

图15b和图15c为码元频率分别为512、1024、1792bps时对应的辨识解及辨识误差率，可以看出随着码元频率的降低，辨识解与解析解的吻合度逐渐增加。当码元频率为1792bps时，辨识误差率在后期超过了5%；当码元频率为1024bps时，辨识误差率有所改善；当码元频率降低到512bps时，辨识误差率最低(1%以内)。与图12c类似，在各误差率曲线中也能观察到与码元频率同频的扰动(图15c)。使用式(4)计算各码元频率对应的辨识信噪比(图15d)，可以看出码元频率每降低512bps可带来3～7dB的辨识信噪比增益。

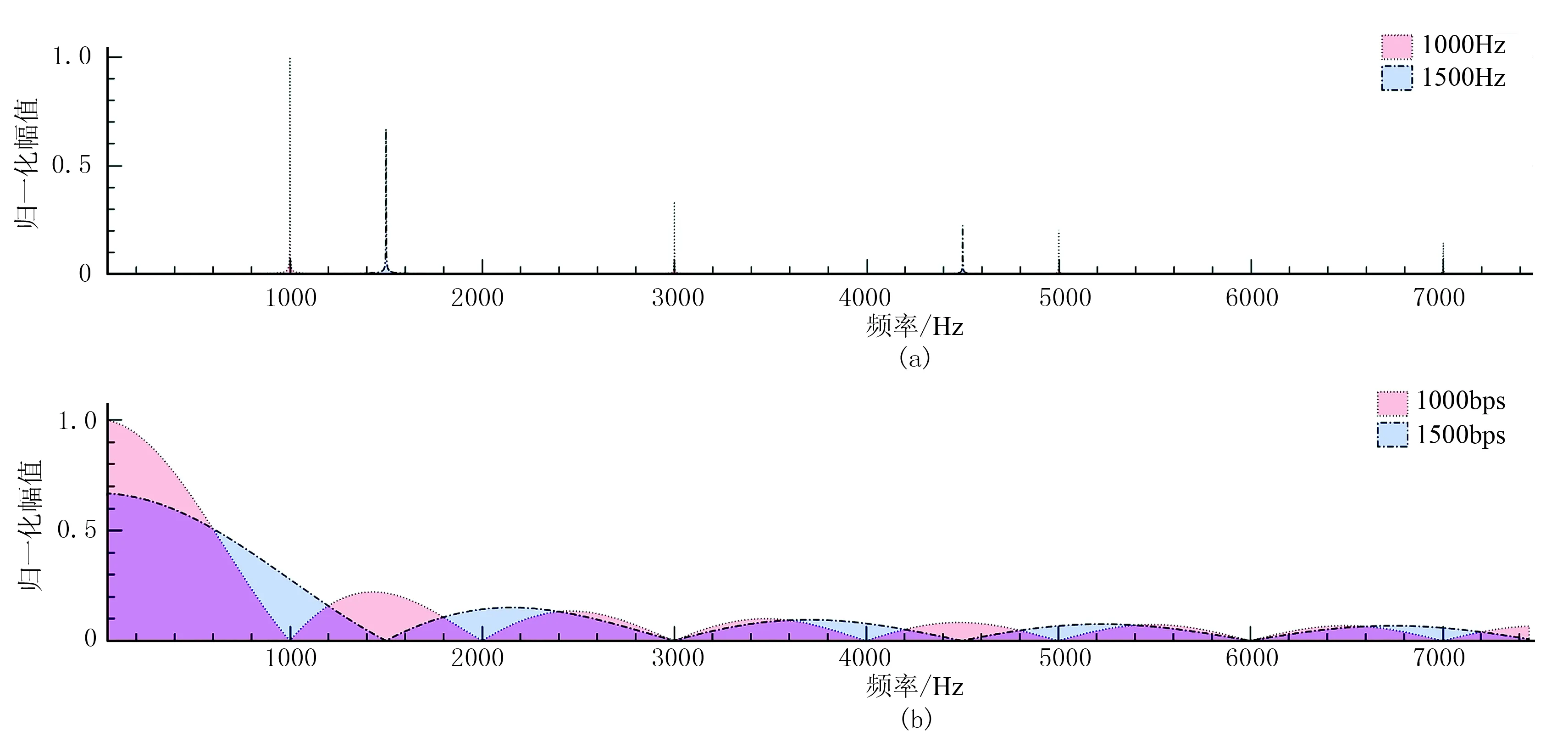
图13 方波与m序列在不同编码频率下的频谱 (a)方波； (b)m序列

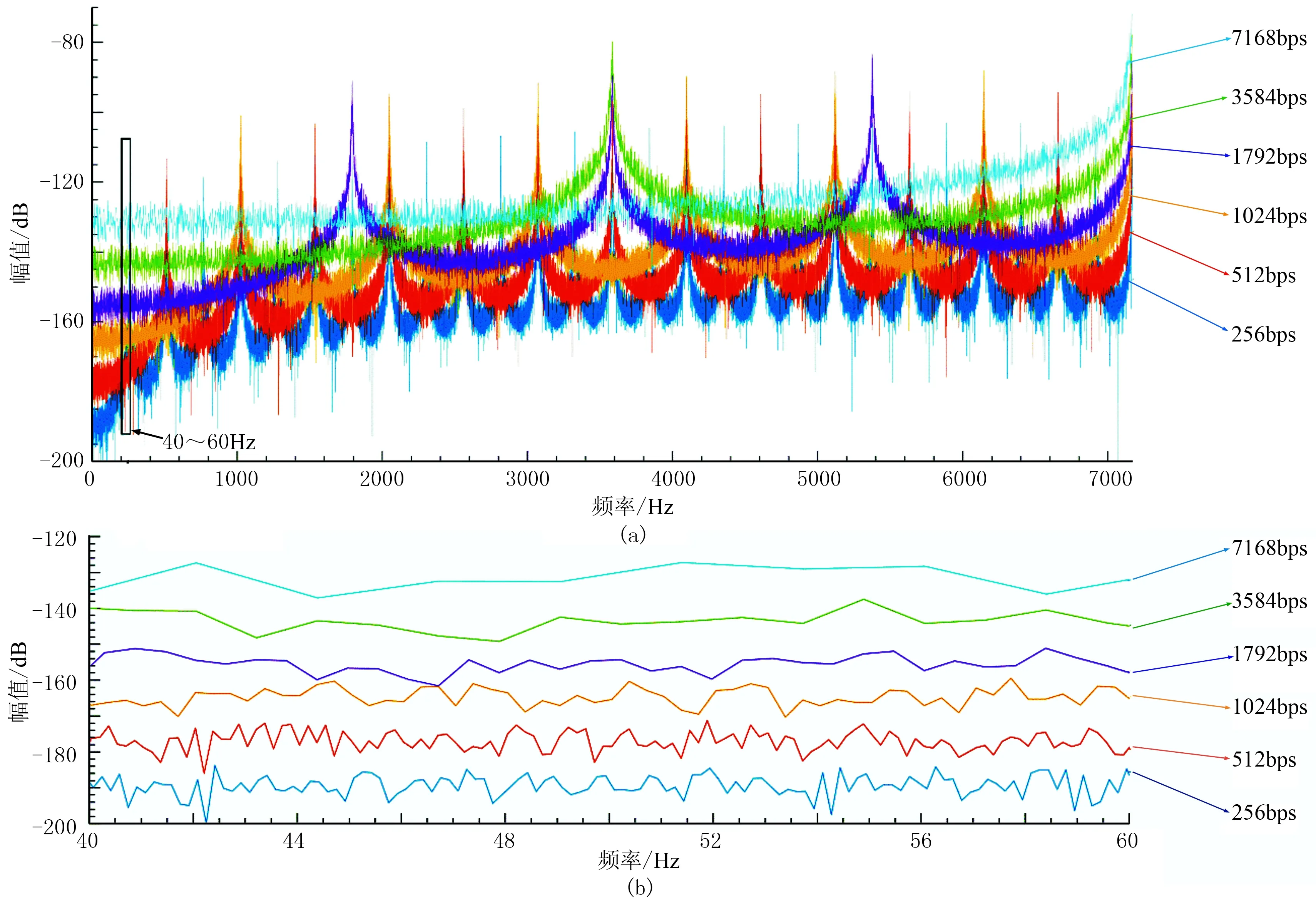
图14 各码元频率对应辨识系统的幅频响应 (a)0～7166Hz； (b)40～60Hz

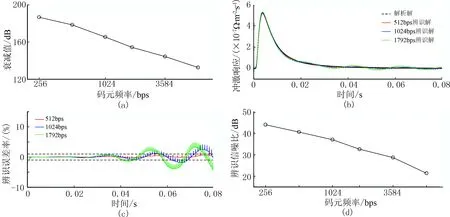
图15 不同码元频率m序列的辨识效果 (a)各码元频率对应辨识系统在50Hz的频响衰减值； (b)各码元频率对应的辨识解； (c)各码元频率对应的辨识误差率曲线； (d)各码元频率对应的辨识信噪比

7 验证试验

为验证数值模拟结果，在中国内蒙古自治区兴和县曹四夭钼矿进行了试验。收—发装置如图16所示，其中供电电流为15A，发射电极间距为300m，接收电极间距为60m，选用960m和660m两种收—发偏移距。

本次试验使用了多种编码参数组合，包含4种阶数，分别是6、8、10、12阶，以及4种码元频率，分别是256、512、1024、1792bps。由于野外试验中大地电磁冲激响应的解析解是未知的，因此无法使用式(4)计算辨识信噪比。为定量分析现场试验中不同编码参数的辨识精度，重新定义现场试验辨识信噪比

(8)

式中：gori(t)为通过原始数据得到的大地电磁冲激响应辨识解；gsmo(t)为gori(t)的平滑结果。显然Pidt与gori(t)的光滑程度成正比，即当gori(t)中含有的噪声分量越少，gori(t)与gsmo(t)吻合度越高，Pidt的值越大。

图17为660m收发距时，分别使用6、8、10、12阶m序列，以1024bps码元频率进行发射得到的大地电磁冲激响应辨识解。图中初始时刻的瞬变脉冲为空气波。很明显，随着阶数的增加，原始辨识解曲线的平滑度逐渐增强，并逼近拟合曲线。用式(8)分别计算4种阶数的现场试验辨识信噪比，并与数值模拟结果进行比较(图18)，可见使用高阶m序列能获得更高的辨识精度，验证了6.1节所述结论。

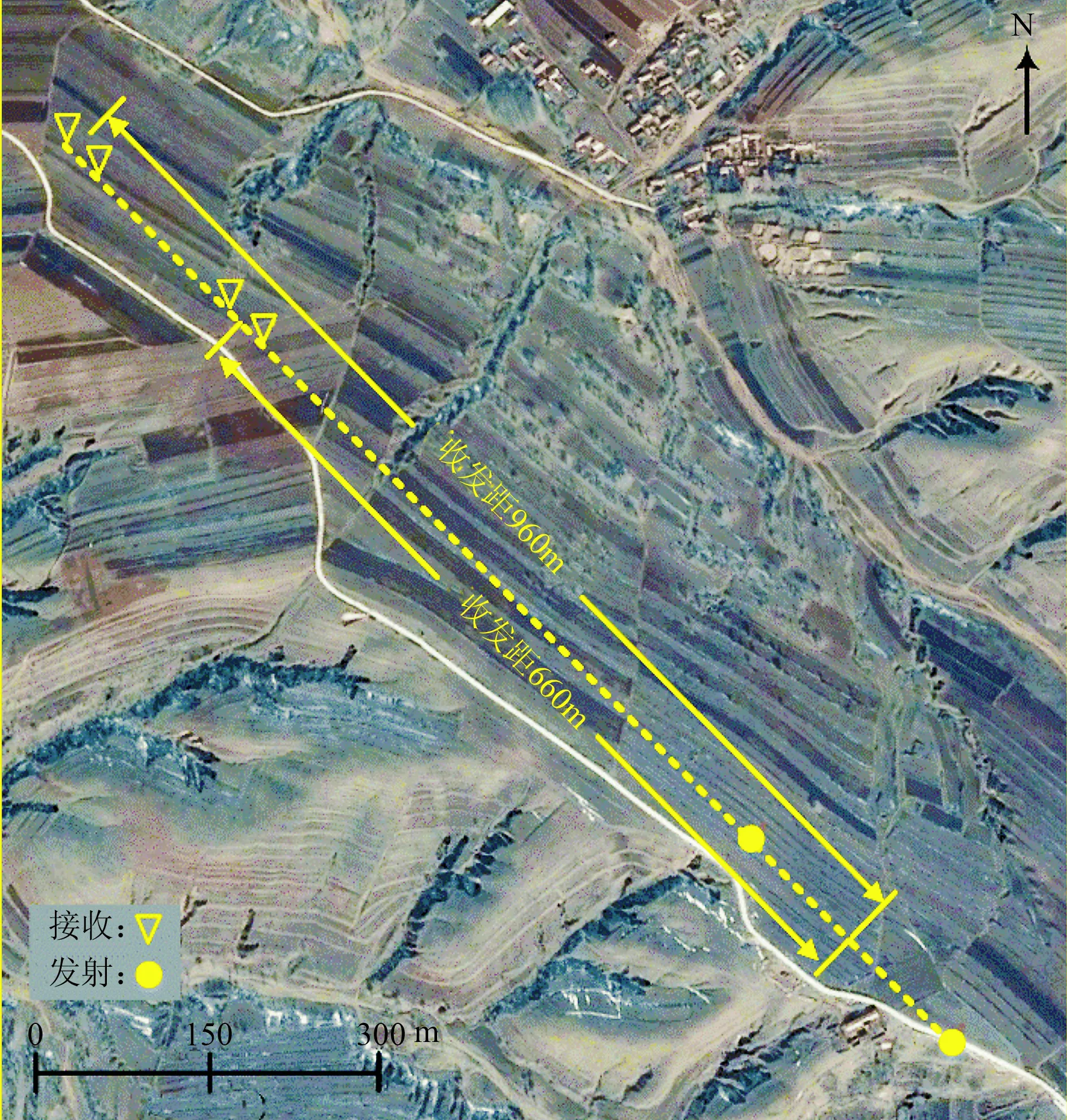
图16 现场试验收—发装置布设示意图

图17 660m收发距时不同阶数m序列的辨识结果 (a)6阶； (b)8阶； (c)10阶； (d)12阶

类似地，对于960m收发距、使用10阶m序列分别以256、512、1024、1792bps码元频率进行编码发射，对应的大地电磁冲激响应辨识解见图19。可见随着码元频率的降低，原始辨识解曲线的平滑度逐渐增加，并逼近拟合结果。

用式(8)计算4种码元频率的现场试验辨识信噪比，并与数值模拟结果进行比较(图20)，可见使用较低的码元频率能够获得更高的辨识精度，验证了6.2节所述结论。

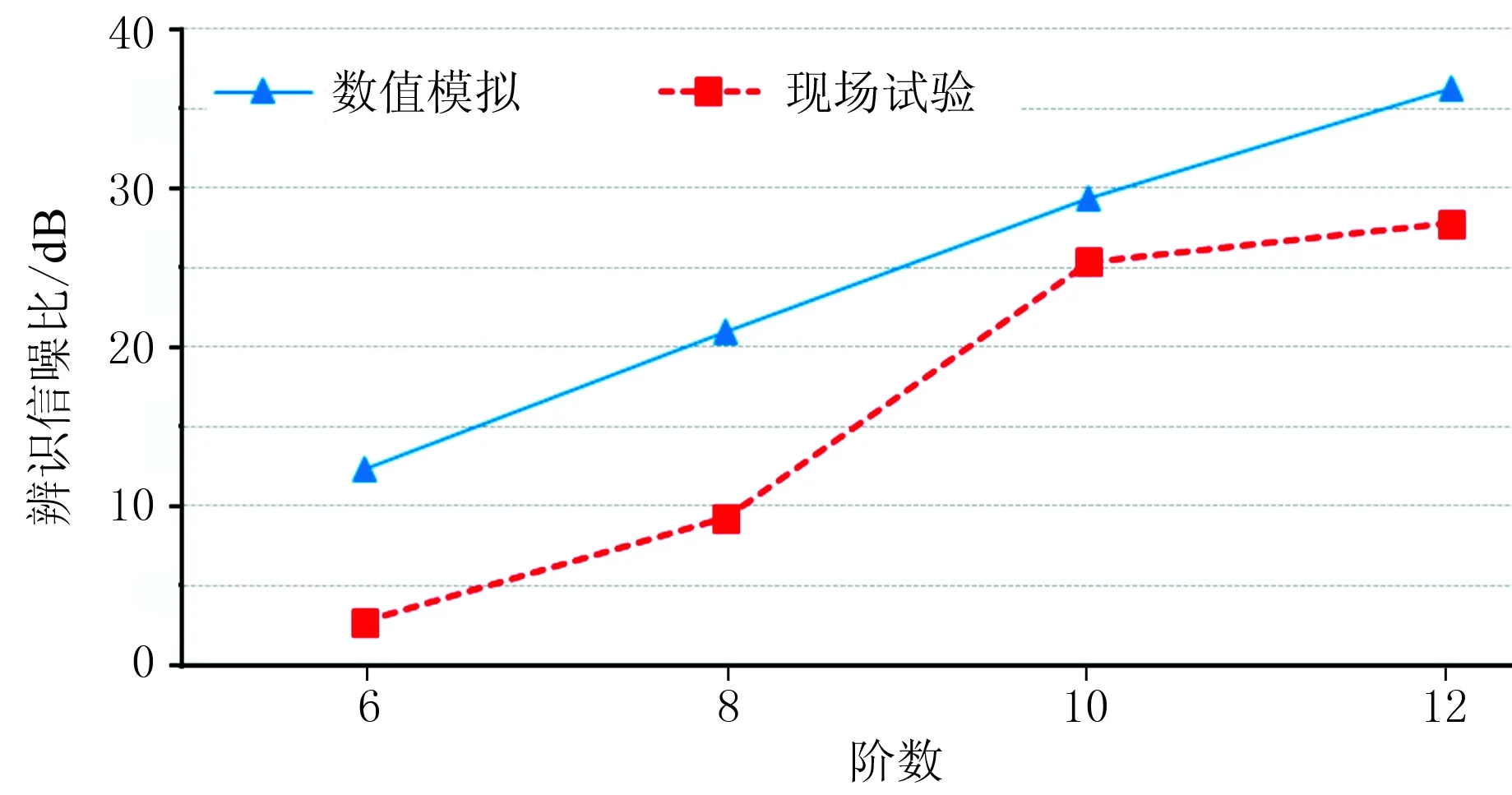
图18 660m收发距时不同阶数对应的辨识信噪比

8 讨论

多个编码参数使得m序列具有灵活多变的编码组合，不同编码组合的m序列在无噪声环境下均能取得较高的辨识精度；当存在噪声干扰时，不同的编码组合体现出不同的抗噪性能。因此编码参数的优化选择成为大地电磁冲激响应高精度辨识的关键，为此需要深入研究m序列的抗噪机制，对不同编码参数m序列的抗噪性能进行定量评估。

关于阶数，高阶m序列具备更强的噪声压制性能，可提高大地电磁冲激响应辨识精度。数值模拟与验证试验表明，相同码元频率下，每增加一阶，可以带来2～7dB的辨识信噪比增益，但是提高阶数的同时会增加发射的时间成本。

关于码元频率，传统的选择方法只能确定码元频率的大概区间，具有一定的“盲目性”和“试探性”。通过引入辨识系统的概念，能够对不同码元频率的辨识效果进行分析，继而得出码元频率的优选方案。辨识系统的幅频响应在码元频率及其谐频处取得峰值，即在上述敏感频点处的噪声压制能力最弱，这也是使用高码元频率辨识出的大地电磁冲激响应存在高频扰动的原因。另一方面，这些敏感频点为辨识过程埋下了隐患：若工区有集中分布在敏感频点的干扰源，那么相对其他频点，辨识过程实际上放大了这些干扰，导致辨识精度大幅下降。另外，辨识系统在敏感频点以外的幅频响应衰减值随着码元频率的降低逐渐提高，因此在满足趋肤深度的基础上选用较低的码元频率能够取得较高的辨识精度。

9 结束语

(1)进行大地电磁冲激响应辨识时，在满足趋肤深度的基础上，应尽量选用高阶低码元频率的m序列作为激励源。

(2)由于辨识过程会放大码元频率及其谐频处的噪声，在选择码元频率时应尽量规避强噪声频点及其谐频值，例如电力线噪声频率50Hz及其谐频。

附录A 维纳反褶积

使用地震法中常用的维纳滤波计算反算子，其思想在于使滤波器的实际输出与期望输出的误差平方和最小。本文的期望输出为单位冲激信号δ(t),则有

s(t)*b(t)=δ(t)

(A-1)

离散化得到

b(n)*s(n)=δ(n)

(A-2)

其输出误差的平方和为

(A-3)

式中：τ为b(n)与s(n)的偏移量；N、M分别为s(n)、b(n)的离散点数。令Q最小，b(n)需满足

(A-4)

解得

(A-5)

定义相关函数

(A-6)

(A-7)

式中：γSS(τ-h)为s(n)关于延迟时间τ-h的自相关函数；γδS(h)为s(n)和δ(n)关于延迟时间h的互相关函数。显然γδs(h)也为冲激信号。

式(A-5)可写为

(A-8)

再写成矩阵形式，b(n)可通过解下列矩阵方程求得

(A-9)

[1] Quincy E A,Davenport W H,Lindsay J E.Preliminary field results on a new transient induction system employing pseudo-noise signals.IEEE Transactions on Geoscience Electronics,1974,12(4):123-133.

[2] Duncan PM,Hwang A,Edward R N et al.The development and applications of a wide band electromagnetic sounding system using a pseudo-noise source.Geophy-sics,1980,45(8):1276-1296.

[3] Wright D,Ziolkowski A,Hobbs B.Hydrocarbon de-tection and monitoring with a multi-componment transient electromagnetic (MTEM) survey.The Leading Edge,2002,21(9):852-864.

[4] Ziolkowski A,Hobbs B,Wright D.Multitransient electromagnetic demonstration survey in France.Geophysics,2007,72(4):F197-F209.

[5] Ziolkowski A,Wright D,Hall G et al.First shallow-water multi-transient EM survey.Geophysical Seminar of Petroleum Exploration Society of Great Britain,Expanded Abstracts,2008，146-149.

[6] 赵碧如,赵健,张洪魁等.PS100型IP到端可控源高精度大地电测仪系统—CDMA技术首次在地电阻率测量中的应用.地球物理学进展,2006,21(2):675-682. Zhao Biru,Zhao Jian,Zhang Hongkui et al.The PS100 high precision earth-electricity instrument system (IP to IP) with controllable source — application of CDMA technology to the measurement of earth resistivity for the first time.Progress in Geophysics,2006,21(2):675-682.

[7] 王忠仁,樊丹丹,高健等.基于三元伪随机编码的可控震源信号设计方法.石油地球物理勘探,2009,44(5):534-536. Wang Zhongren,Fan Dandan,Gao Jian et al.Vibroseis signal designing based on ternary pseudo-random co-ding technology.OGP,2009,44(5):534-536.

[8] 汤井田,罗维斌.基于相关辨识的逆重复m序列伪随机电磁法.地球物理学报,2008,51(4):1226-1233. Tang Jingtian,Luo Weibin.Pseudo-random electromagnetic exploration based on invert-repeated m sequence correlation identification.Chinese Journal of Geophysics,2008,51(4):1226-1233.

[9] 王显祥,底青云,邓居智.多通道瞬变电磁法油气藏动态检测.石油地球物理勘探,2016,51(5):1021-1030. Wang Xianxiang,Di Qingyun,Deng Juzhi.Reservoir dynamic detection based on multi-channel transient electromagnetic.OGP,2016,51(5):1021-1030.

[10] Helwig S L,Hanstein T,Hoerdt A.The VIBR OTEM method.SEG Technical Program Expanded Abstracts,1999,18:283-285.

[11] 罗维斌,李庆春,汤井田.编码电磁测深.地球物理学报,2012,55(1):341-349. Luo Weibin,Li Qingchun,Tang Jingtian.Coded source electromagnetic sounding method.Chinese Journal of Geophysics,2012,55(1):341-349.

[12] Ziolkowski A.Wiener estimation of the Green’s function.Geophysics,2013,78(5):W31-W44.

[13] Ilyichev P V and Bobrovsky V V.Application of pseudo-noise signals in systems of active geoelectric exploration (Results of mathematical simulation and field experiments).Seismic Instruments,2015,51(1):53-64.

[14] Ziolkowski A.Development in the transient electro-magnetic method.First Break,2007,25(6):99-106.

[15] 武欣,薛国强,底青云等.伪随机编码源电磁响应的精细辨识.地球物理学报,2015,58(8):2792-2802. Wu Xin,Xue Guoqiang,Di Qingyun et al.Accurate identification for the electromagnetic impulse response of the earth with pseudo random coded waveforms.Chinese Journal of Geophysics,2015,58(8):2792-2802.

[16] 王显祥,底青云,王妙月等.基于m伪随机序列的电磁法抗噪能力分析.地球物理学报,2016,59(5):1861-1874. Wang Xianxiang,Di Qingyun,Wang Miaoyue et al.A study on the noise immunity of electromagnetic me-thods based on m pseudo-random sequence.Chinese Journal of Geophysics,2016,59(5):1861-1874.

[17] 蔡志东,刘聪伟,王勇等.井地联合地震数据反褶积.石油地球物理勘探,2017,52(1):8-12. Cai Zhidong,Liu Congwei,Wang Yong et al.Seismic data deconvolution with VSP operator.OGP,2017,52(1):8-12.

[18] 李钟晓,李振春.基于交替分裂Bregman迭代算法的鲁棒多道预测反褶积方法.石油地球物理勘探,2017,52(4):678-688. Li Zhongxiao and Li Zhenchun.Robust multichannel predictive deconvolution based on the alternating split Bregman iteration algorithm.OGP,2017,52(4):678-688.

[19] 淳少恒,陈儒军,耿明会.伪随机m序列及其在电法勘探中的应用进展.地球物理学进展,2014,29(1):439-446. Chun Shaoheng,Chen Rujun,Geng Minghui.Review of the pseudo-random m sequence and its application in the electrical prospecting of exploration geophy-sics.Progress in Geophysics,2014,29(1):439-446.

[20] 林可祥,汪一飞.伪随机码的原理与应用．北京:人民邮电出版社,1978.

[21] Weir G.Transient electromagnetic fields about an infinitesimally long grounded horizontal electric dipole on the surface of a uniform half-space.Geophysical Journal of the Royal Astronomical Society,2010,61(1):41-56.

[22] 薛国强.论瞬变电磁测深法的探测深度.石油地球物理勘探,2004,39(5):575-578. Xue Guoqiang.On surveying depth by transient electromagnetic sounding method.OGP,2004,39(5):575-578.