利用三参数AVO近似方程的深层叠前地震反演
印兴耀 王慧欣 曹丹平 周琦杰 郭淑文
(①中国石油大学(华东)地球科学与技术学院,山东青岛 266580; ②中国石化上海海洋油气分公司勘探开发研究院,上海 200120; ③中国石油大港油田勘探开发研究院,天津 300280)
1 引言
随着油气勘探领域、深度的扩展,深层油气勘探已成为地球物理勘探的重点,因而深层油气储层的叠前地震反演和流体识别方法成为研究热点。由于受埋藏深度的影响,深层储层地震资料往往表现出入射角范围窄、照明度不足、信噪比和分辨率较低、阻抗差异小、AVO反射特征不明显等特征,给地震反演(尤其是叠前反演)带来了新的挑战。针对深层储层资料的这些特征及储层流体识别的难题,印兴耀等[1]和刘晓晶等[2]分别采用对深层储层较为敏感的Russell因子和Gassmann流体项,对埋藏较深的构造—岩性复合圈闭及以深水砂砾岩为主导的隐蔽油气藏进行流体识别,都取得了较好应用效果,但Russell和Gassmann等流体因子易受孔隙度等因素影响而产生流体识别的假象。
Yin等[3]基于孔隙介质理论,依据临界孔隙度模型和突出流体体积模量Kf的Gassmann流体项经验公式推导出基于流体体积模量Kf、固体刚性参数fm、密度ρ和孔隙度φ的四参数AVO近似式。与常规流体因子相比,流体体积模量Kf只与流体有关而不受孔隙度影响,减少了流体识别的假象,显著提高了流体识别的可靠性。虽然该方法已取得较好效果,但在实际应用中仍存在一定局限性: ①该近似式的反射系数之间并不是完全独立的; ②该方法需要四个角道集。
针对上述问题,本文根据深层地震资料入射角范围较窄和常规流体因子敏感性较低的特点,沿用了对储层较为敏感的流体体积模量Kf[3],基于Xu-White模型和岩石物理统计特征,厘清了固体刚性参数fm与孔隙度φ之间的指数关系,并推导出流体体积模量Kf、固体刚性参数fm和密度ρ的三参数AVO近似方程。模型和实际资料的应用结果表明本文提出的近似方程在窄角度情况下的精度和稳定性均满足反演的要求,而且在应用中具有现实的可行性。
2 Kf-fm-ρ三参数AVO近似方程和反演
2.1 Kf-fm-ρ三参数AVO近似方程推导
Gassmann流体项f作为储层流体识别的重要参数,在目前的实际应用中已取得较好效果,但本身受流体和固体骨架双重作用,易受骨架和孔隙度等参数影响而形成流体识别假象。当采用流体体积模量Kf作为流体因子进行流体识别时可对固体骨架影响和流体效应进行解耦,因此在指示流体性质方面具一定优势。
Yin等[3]参考Nur等[4]、Batzle等[5]和Han等[6]岩石物理的研究成果,推导出基于流体体积模量的Kf-fm-ρ-φ四参数AVO近似方程
(1)
式中:γdry是干岩石纵横波速度比;γsat是饱和岩石纵横波速度比;Kf为流体体积模量;fm=φμ,为固体刚性参数,其中φ为孔隙度,μ为剪切模量;ρ为密度。
式(1)中包含的固体刚性参数fm与孔隙度φ之间存在关系fm=φμ,因此该反射系数之间并不是完全独立的; 其次,该方法需要四个角道集,反演条件数也随之增加,导致稳定性降低; 另外,对于入射角范围较窄的深层储层而言,在有限角度信息中提取四个具有一定差异且可用于反演的角道集是较困难的,因此该方法并不适用于窄角度深层储层。所以本文在式(1)基础上,根据Xu-White模型,推导出基于流体体积模量Kf、固体刚性参数fm和密度ρ的三参数AVO近似方程,其中流体体积模量Kf可通过弹性阻抗反演稳定地提取并应用于深层储层的流体识别。
剪切模量μ主要与骨架、骨架矿物和孔隙度有关,受含水饱和度和流体的影响比较小。图1是基于Xu-White模型,泥质含量(SH)从40%变化到100%,φ从10%变化到30%时,φ与μ的关系图。经过大量实际资料的交会分析,得知φ与μ之间具有一定的指数关系。图2是中国东部某实际工区的φ与μ的岩石物理交会图。根据图1和图2中的岩石物理关系特征图,可建立φ与μ之间的指数关系。
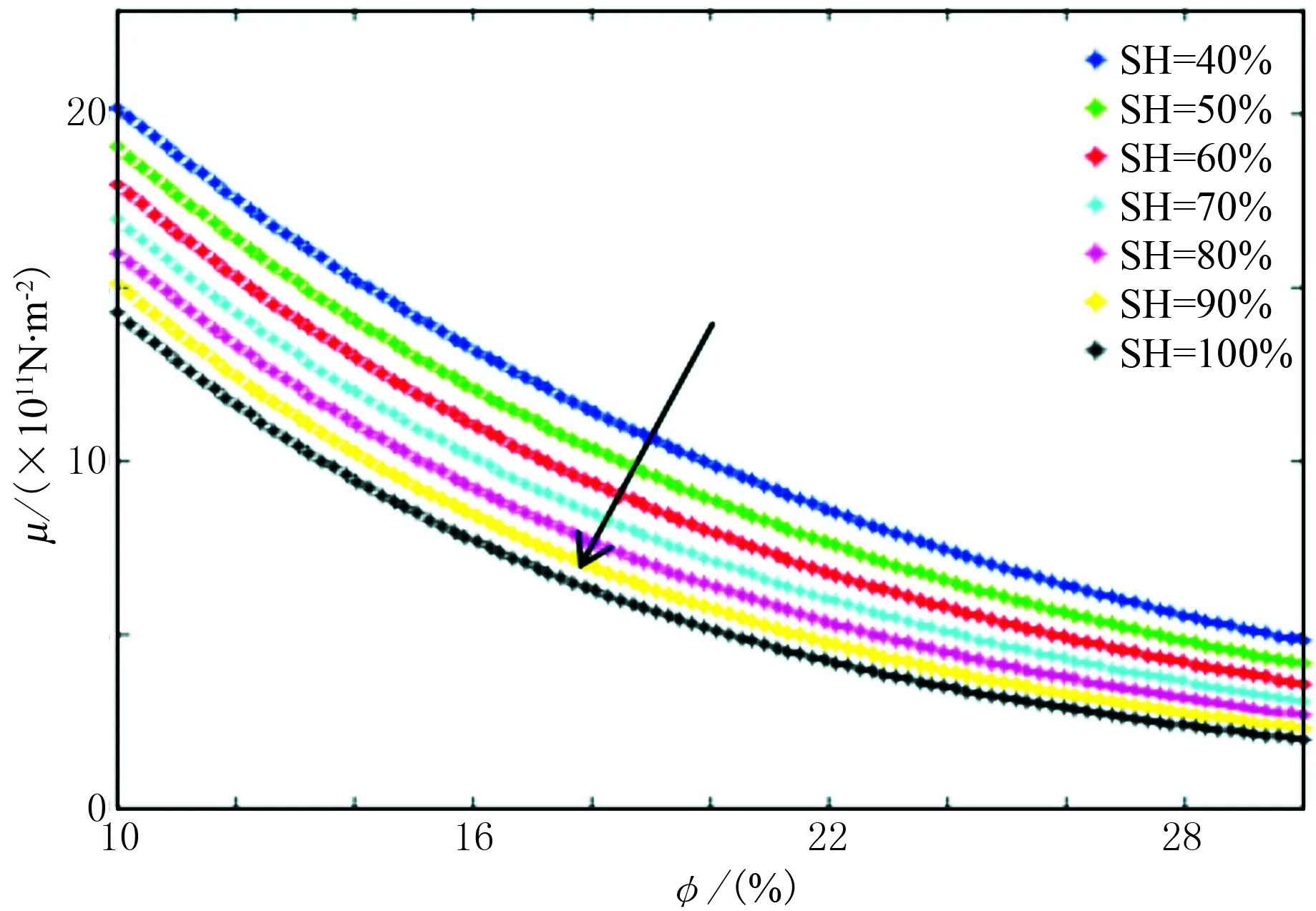
图1 不同泥质含量时孔隙度φ与剪切模量μ的关系
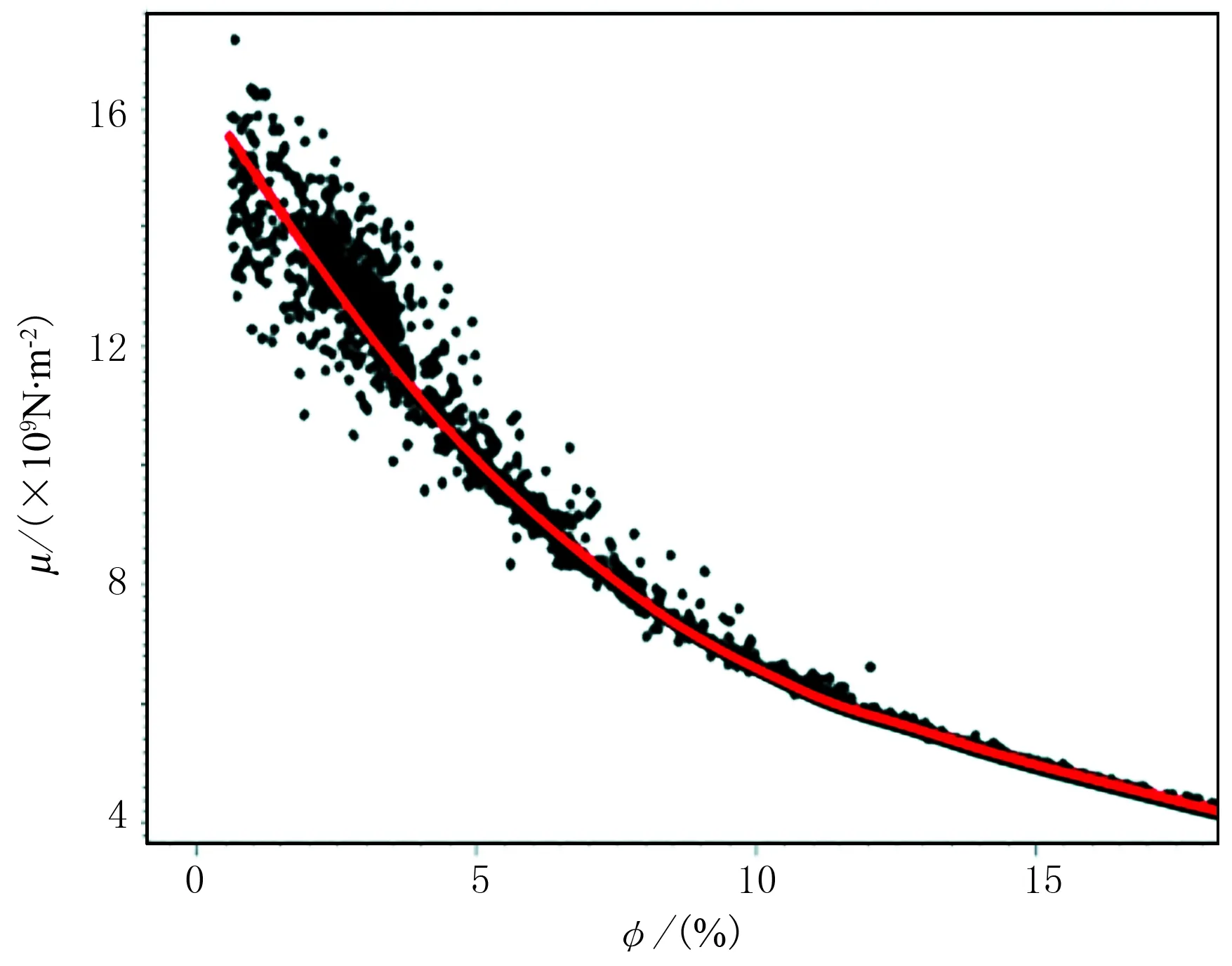
图2 实际工区孔隙度φ与剪切模量μ的交会图
根据实际工区特点和岩石物理统计规律,建立φ与μ之间的指数关系
μ=aφα
(2)
据前述关系式,得到
fm=μφ=aφαφ=aφ1+α
(3)
令1+α=r,有
fm=aφr
(4)
式(2)~式(3)中a和r是根据实际工区特点建立的有关φ与μ之间的拟合系数。
(5)
将式(5)代入式(1)可得到基于Kf、fm和ρ的三参数AVO近似方程

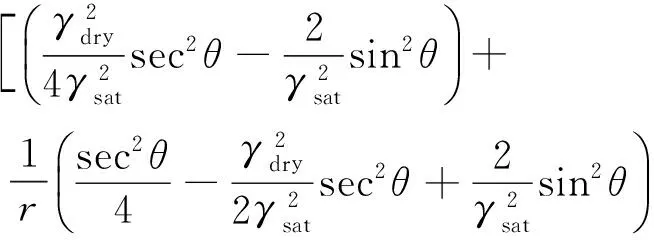
(6)
2.2 Kf-fm-ρ三参数AVO近似方程精度分析
为了对式(6)进行精度检验,设计模型参数如表1的深层砂岩模型,其上覆地层是含气砂岩,下伏地层是含水砂岩。分别用精确Zoeppritz方程、式(1)和式(6)计算得到地层界面处反射系数(图3)。
从图3可看出当入射角较小时,式(6)与Zoep-pritz方程的精度相当,反射系数曲线几乎重合,而且其精度高于由式(1)得到的反射系数,但随着角度的增加,误差逐渐增大。模型精度分析表明式(6)满足深层储层反演对精度的要求。

表1 深层砂岩模型参数
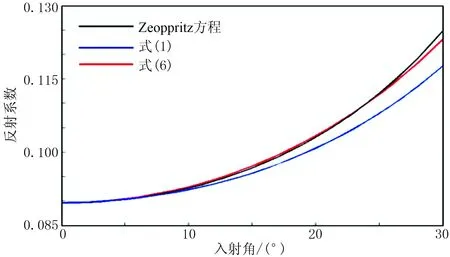
图3 深层含气砂岩模型反射系数对比图
参考Connolly[7]和Whitcombe[8]提出的弹性阻抗以及标准化的概念,推导出有关流体体积模量Kf的三参数标准化弹性阻抗公式
(7)
其中
(8)
对式(7)取自然对数,并将其进行线性化变换
(9)
对于一道有n个采样点的地震数据,可构建如下矩阵
(10)
分别将三个角度的弹性阻抗和井旁道数据代入式(10)中,可以得到三个角度对应的九个系数a(θi)、b(θi)、c(θi)(其中i=1,2,3),将此九个系数代入下列方程组中
(11)
可得流体体积模量、固体刚性参数和密度。
2.3 三参数AVO近似式信息量分析
在AVO近似公式中不同的弹性参数所对应的反射系数的信息比重有所不同,因此不同的弹性参数的反演可靠性也存在一定的差异。为了研究利用式(6)反演弹性参数的可行性,采用Nicolao等[9]提出的信息敏感分析方法,定量分析式(6)中的弹性参数的信息敏感性。
将式(6)以如下形式表示
R(θ)=G(θ)m
(13)
式中


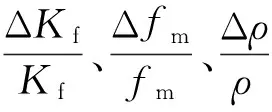

图4 模型空间中的三个特征值(a)及特征向量方向余弦(b)随最大入射角度的变化曲线
2.4 三参数AVO近似式稳定性分析
稳定性对反演(尤其是当数据不够完备时)非常重要。图5是相同条件下基于式(1)和式(6)系数矩阵的条件数的常用对数对比。当最大入射角从20°增大到30°时,两个条件数都有减小的趋势,但基于式(1)系数矩阵的条件数都明显大于式(6),表明随着最大入射角的增加,基于Kf的四参数和三参数AVO近似方程的稳定性都随之提高,但后者的稳定性明显高于前者。

图5 基于式(6)和式(1)系数矩阵条件数分析
精度分析表明,当入射角较小时,式(6)与Zoeppritz方程精度相当; 稳定性分析表明式(6)的稳定性明显高于式(1),因此式(6)满足反演的精度和稳定性要求。
3 模型试算
首先通过实际井资料计算得到Kf、fm和ρ的测井曲线,利用上述井数据与35Hz雷克子波进行褶积得到CMP道集,再通过合理的角度部分叠加得到三个角度(5°,15°,25°)部分叠加道集,最后利用式(6)进行弹性阻抗反演。图6是在无噪和信噪比SNR=2∶1情况下,通过弹性阻抗反演得到的Kf、fm和ρ曲线。图7是无噪和SNR=2∶1时提取的Kf和ρ的相对误差。可见在无噪时Kf、fm和ρ的反演结果与模型数据几乎重合,相对误差都较小; 当SNR=2∶1时,Kf的反演结果受到一定影响,其总体趋势仍与模型数据基本吻合,但fm和ρ的反演结果较差,相对误差也明显增大; 另外,这两种情况下,Kf反演结果的相对误差(集中分布在8%附近)都小于ρ。由于fm=φμ,实际测井数据中孔隙度φ信息含量十分匮乏; 密度项反演结果较差,原因是由于密度项的量纲远小于其他两项,而且变化不够明显,导致反射系数的信息量相对较小。模型测试结果表明: 本文方法在反演过程中具有较好的抗噪性,可有效地提取流体体积模量参数,从而为深层储层流体识别提供了较为可靠的数据支撑。
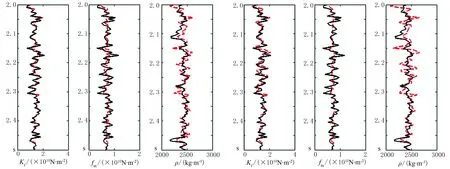
图6 无噪(左)和SNR=2∶1(右)时的三参数反演结果 黑色实线为模型数据,红色虚线为反演结果
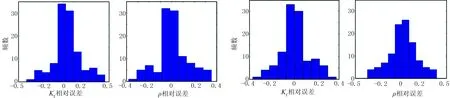
图7 无噪(左)和SNR=2∶1(右)时提取的Kf和ρ的相对误差统计
4 实际资料应用
将本文的弹性阻抗反演方法应用于中国东部陆上M深层油田,其目的储层埋深达4500m,对应时间约为3s,最大入射角是24°,只提取到三个(5°、15°、25°)可用于反演的角度道集,物性数据较差,地震资料入射角范围较窄。利用岩石物理交会图(图8)和Dillion等[10]提出的流体因子敏感性定量分析方法对该工区测井资料进行比较分析,发现流体体积模量Kf对目的层最为敏感(图9)。
将叠前CMP道集转换到角度域后,进行角度部分叠加得到三个角度部分叠加剖面,再利用本文叠前弹性阻抗方法进行反演,提取到流体因子Kf和密度ρ剖面(图10,插入的测井解释柱状图中红色代表油层、粉色代表水层)。在Kf的反演结果与测井解释结果吻合较好,油层出现明显的偏小趋势,可区分油层和水层(图10a); 在ρ的反演结果中油层与水层数值差别较小,难以区分油层和水层(图10b)。因此,本文提出的利用弹性阻抗提取流体体积模量Kf方法在实际应用中具有现实性和可靠性,在深层储层的流体识别中具有明显优势。

图8 流体体积模量与固体刚性参数交会图
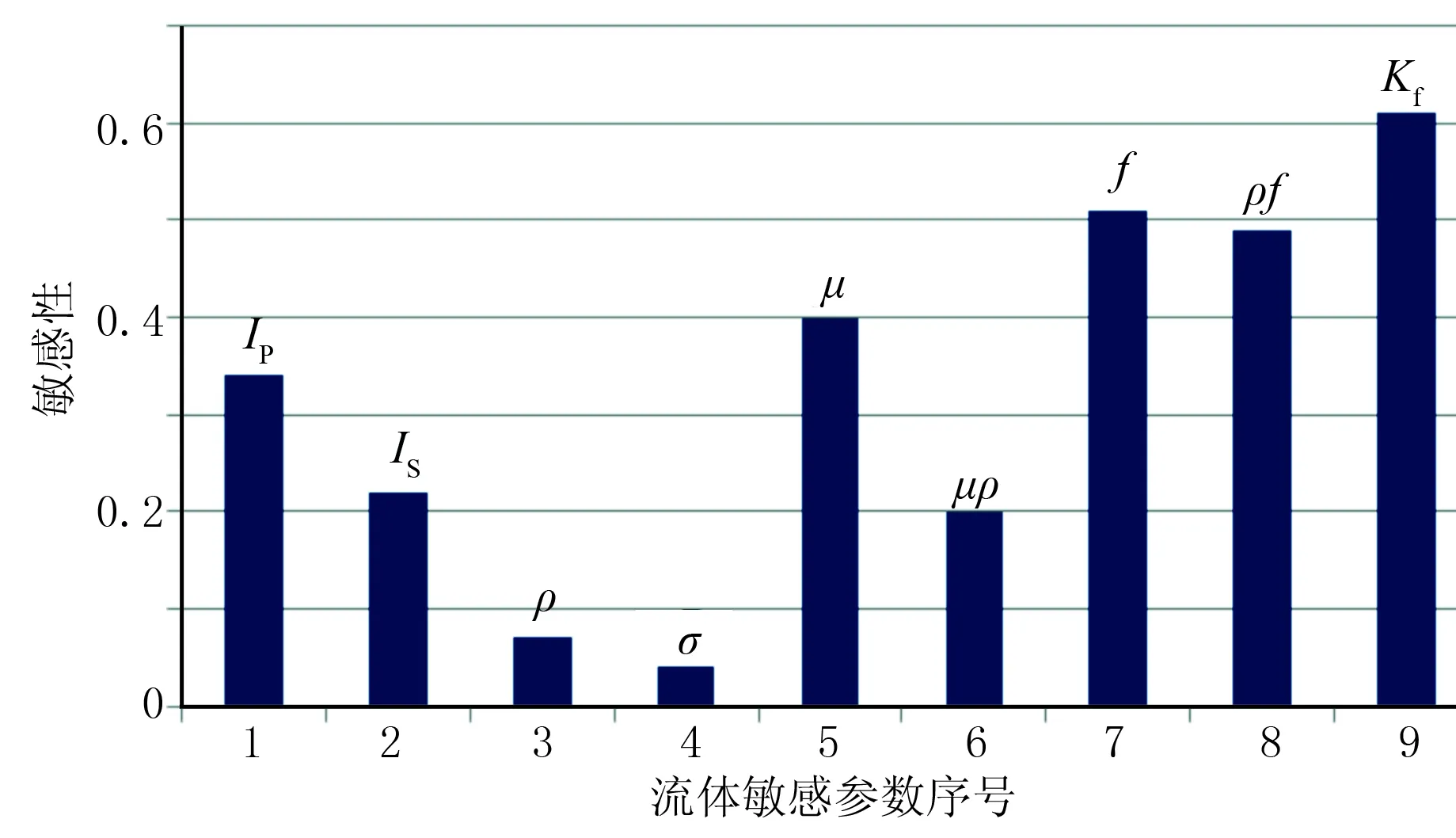
图9 流体敏感性分析
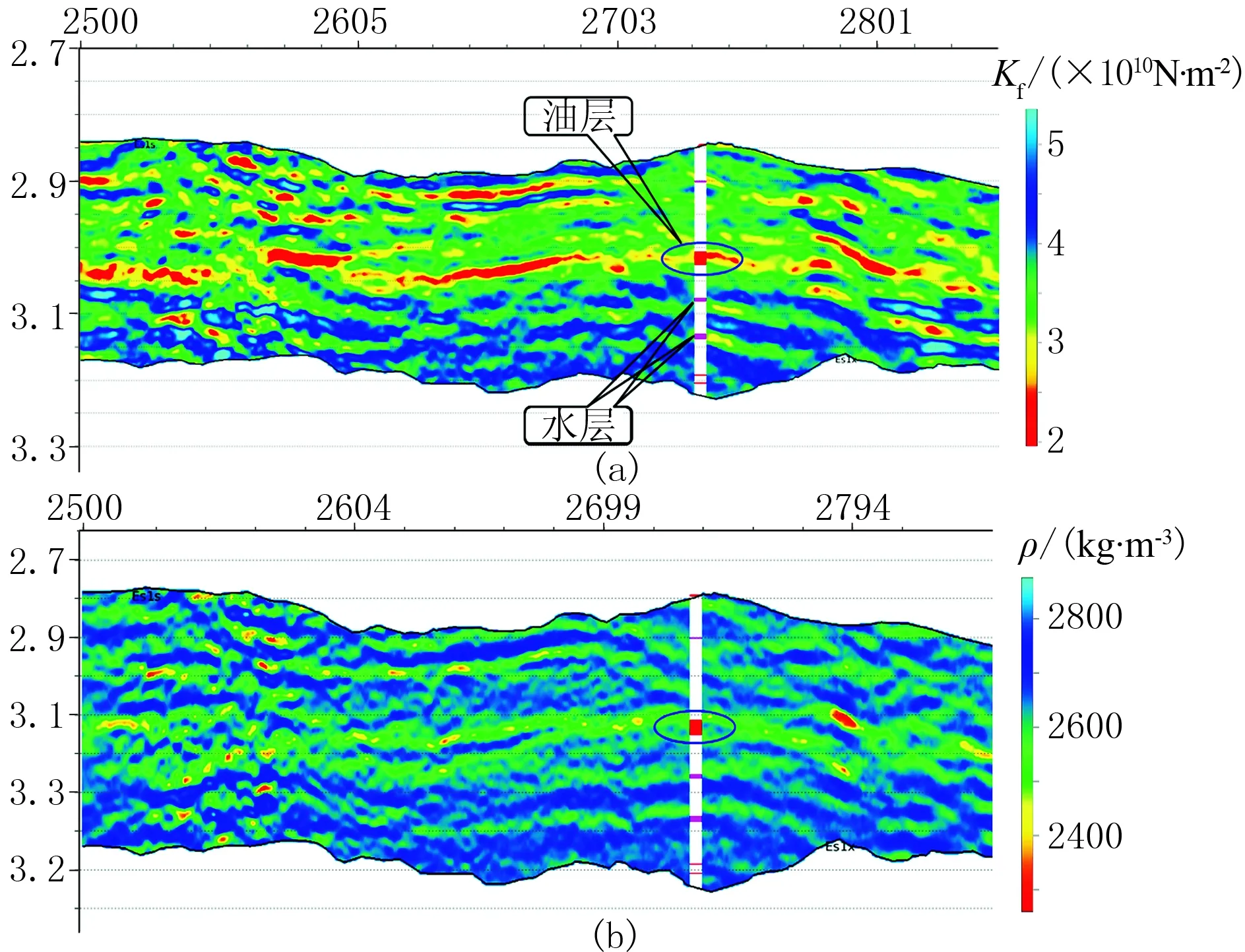
图10 流体体积模量(a)和密度(b)反演剖面
5 结论
(1)本文在Xu-White模型基础上,根据岩石物理特征以及实际工区统计规律,推导出了针对深层窄角度的基于流体体积模量Kf、固体刚性参数fm和密度ρ的三参数AVO近似方程及弹性阻抗方程;
(2)Kf-fm-ρ三参数AVO近似方程只需要三个角度叠前地震数据,且三参数反射系数之间相关性较低;
(3)Kf-fm-ρ三参数AVO近似方程与精确Zoeppritz方程的精度相当,误差较小,而且其条件数也明显小于Kf-fm-ρ-φ四参数AVO近似方程,因此本文所述方法能满足反演对精度和稳定性的要求;
(4)Kf作为流体因子,在进行流体识别时对目的层的敏感度较高;
(5)模型测试和实际资料应用表明三参数AVO近似方程及其弹性阻抗方程在针对窄角度的深层储层进行流体识别时,具有较好的稳定性和实用性。
本文所述方法仍具有一定局限性,它不适用于低孔隙度的致密储层,这是由于式(1)在推导过程中主要引用了Nur等[4]的临界孔隙度模型和Han等[6]的岩石物理统计规律,这些理论都是基于孔隙度较大情况下提出的,因此本文的方法更适用于孔隙度相对较大的深层储层。
[1] 印兴耀,张世鑫,张峰.针对深层流体识别的两项弹性阻抗反演与Russell流体因子直接估算方法研究.地球物理学报,2013,56(7):2378-2390. Yin Xingyao,Zhang Shixin,Zhang Feng.Two-term elastic impedance inversion and Russell fluid factor direct estimation method for deep reservoir fluid identification.Chinese Journal of Geophysics,2013,56(7):2378-2390.
[2] 刘晓晶,印兴耀,吴国忱等.基于基追踪弹性阻抗反演的深部储层流体识别方法.地球物理学报,2016,59(1):277-286. Liu Xiaojing,Yin Xingyao,Wu Guochen et al.Identification of deep reservoir fluids based on basis pursuit inversion for elastic impedance.Chinese Journal of Geophysics,2016,59(1):277-286.
[3] Yin Xingyao and Zhang Shixin.Bayesian inversion for effective pore-fluid bulk modulus based on fluid-matrix decoupled amplitude variation with offset approximation.Geophysics,2014,79(5):R221-R232.
[4] Nur A,Mavko G,Dvorkin J et al.Critical porosity:A key to relating physical properties to porosity in rocks.The Leading Edge,1998,17(3):357-362.
[5] Batzle M,Hofmann R,Han D H et al.Fluids and frequency dependent seismic velocity of rocks.The Leading Edge,2001,20(2):168-171.
[6] Han Dehua and Batzle M L.Gassmann’s equation and fluid-saturation effects on seismic velocities.Geophysics,2004,69(2):398-405.
[7] Connolly P.Elastic impedance.The Leading Edge,1999,18(4):438-452.
[8] Whitcombe D N.Elastic impedance normalization.Geo-physics,2002,67(1):60-62.
[9] Nicolao A D,Drufuca G,Rocca F.Eigen values and eigenvectors of linearized elastic inversion.Geophy-sics,1993,58(5):670-679.
[10] Dillon L,Schwedersky G,Vásquez G et al.A multi-scale DHI elastic attributes evaluation.The Leading Edge,2003,22(10):1024-1029.
[11] 印兴耀,李超,张世鑫.基于双相介质的地震流体识别.中国石油大学学报(自然科学版),2013,37(5):38-43. Yin Xingyao,Li Chao,Zhang Shixin.Seismic fluid discrimination based on two-phase media theory.Journal of China University of Petroleum (Edition of Natural Science),2013,37(5):38-43.
[12] 印兴耀,曹丹平,王保丽等.基于叠前地震反演的流体识别方法研究进展.石油地球物理勘探,2014,49(1):22-34,46. Yin Xinygao,Cao Danping,Wang Baoli et al.Research progress of fluid discrimination with pre-stack seismic inversion.OGP,2014,49(1):22-34,46.
[13] 印兴耀,宗兆云,吴国忱.岩石物理驱动下地震流体识别研究.中国科学:地球科学,2015,01:8-21. Yin Xingyao,Zong Zhaoyun,Wu Guochen.Research on seismic fluid identification driven by rock physics.Science China Earch Sciences,2015,58:159-171.
[14] 印兴耀,刘欣欣.储层地震岩石物理建模研究现状与进展.石油物探,2016,55(3):309-325. Yin Xingyao,Liu Xinxin.Research status and progress of the seismic rock-physics modeling methods.GPP,2016,55(3):309-325.
[15] Russell B H,Gray D,Hampson D P.Linearized AVO and poroelasticity.Geophysics,2011,76(3):C19-C29.
[16] Shuey R.A simplification of the Zoeppritz equations.Geophysics,1985,50(4):609-614.
[17] Smith G,Gidlow P.Weighted stacking for rock property estimation and detection of gas.Geophysical Prospecting,1987,35(9):993-1014.
[18] Quakenbush M,Shang B,Tuttle C.Poisson impedance.The Leading Edge,2006,25(2):128-138.
[19] Gray D.Elastic inversion for Lamé parameters.SEG Technical Program Expanded Abstracts,2002,21.
[20] Biot M A.Theory of propagation of elastic waves in a fluid-saturated porous solidⅡ:Higher frequency range.Journal of the Acoustical Society of America,1956,28(2):179-191.
[21] Russell B H,Hedlin K,Hilterman F J et al.Fluid-
property discrimination with AVO:A Biot-Gassmann perspective.Geophysics,2003,68(1):29-39.
[22] Russell B H,Gray D,Hampson D P et al.Linearized AVO and poroelasticity.CREWES Research report,2006,18:1-25.
[23] 邓炜,印兴耀,宗兆云.等效流体体积模量直接反演的流体识别方法.石油地球物理勘探,2017,52(2):315-325. Deng wei,Yin Xingyao,Zong Zhaoyun.Fluid identification based on direct inversion of equivalent fluid bulk modulus.OGP,2017,52(2):315-325.
[24] 印兴耀,张世鑫,张繁昌等.利用基于Russell近似的弹性波阻抗反演进行储层描述和流体识别.石油地球物理勘探,2010,45(3):373-380. Yin Xingyao,Zhang Shixin,Zhang Fanchang et al.Utilizing Russell approximation based elastic wave impedance inversion to conduct reservoir description and fluid identification.OGP,2010,45(3):373-380.
[25] 郑笑雪,杜启振,孟宪军等.横向约束分步叠前弹性参数反演.石油地球物理勘探,2017,52(4):760-769. Zheng Xiaoxue,Du Qizhen,Meng Xianjun et al.Lateral constraint two-step prestack elastic parameter inversion.OGP,2017,52(4):760-769.

