基于SL0的高分辨率Radon变换及数据重建
薛亚茹 王 敏 陈小宏
(中国石油大学(北京)地球物理与信息工程学院,北京 102249)
1 引言
由于地震数据在Radon变换域的物理特征直观明确,利于对比分析,因此Radon变换在勘探地震学领域,如平面波分解[1]、去噪[2]、数据恢复[3]、多次波压制[4-6]等方面得到广泛应用。Radon变换算子的非正交性导致直接进行Radon正、反变换时能量的不对等性,于是基于最小范数反演思想的Radon变换被提出。该方法虽然减少了拖尾现象,但会产生平滑效应,不能集中足够能量,在Radon域分辨率较低[7]。因此,要想提高Radon变换的分辨率,则必须对反演稀疏约束的方法进行改进。Sacchi等[8,9]提出在频率域通过柯西稀疏约束提高Radon变换的分辨率,主要通过数据的先验信息修正反演算子,使变换后的能量在Radon域得到收敛,这样不仅有效地消除了空间褶积(或有限孔径)的影响,同时也进一步提高了解的稳定性。高分辨率Radon变换法是一种稀疏约束反演算法[10],目前常用的最小范数约束方法是在频率域通过柯西或L1范数稀疏约束提高Radon变换的分辨率,但作为L0范数的凸逼近形式,L1范数不具有真正意义上的稀疏,它是一种凸松弛算法[11,12]。L0范数是度量数据稀疏度的最好方法,所以为了达到真正的稀疏,要寻求一种严格的L0范数来约束Radon变换。
因求解L0范数计算量巨大,故在实际应用中不断推出新的稀疏优化方法[13-19]。Mohimani等[13,14]提出平滑L0范数(Smoothed L0Norm,SL0)算法,这是一种基于过完备稀疏分解的快速算法,能直接实现L0范数最小化。该算法具有重构前不需知道信号的稀疏度、计算量小、高匹配度以及重建时间短等优点[20],可有效地应用于稀疏信号重构。基于SL0范数算法,Zayyani等[16]、Ghalehjegh等[17]和林婉娟等[18]相继提出TSL0(Thresholded SL0)算法、BSL0(Block SL0)算法和NSL0算法。曹静杰等[21]还提出在Curvelet域的零范数稀疏最优化方法,很好地实现了地震数据的重构,明显提高了计算效率。
本文将SL0范数稀疏约束引入Radon变换,可提高地震数据在Radon域的能量聚焦效果。利用该方法实现缺失地震道重构[22],通过理论模型和实际数据实验与柯西稀疏约束的高分辨率Radon变换方法作比较,证明L0范数稀疏约束的Radon变换更具有优越性。
2 基本原理及实现
2.1 SL0范数定义
一个向量的L0范数是这个向量的不连续函数,直接使用L0范数存在很多问题。为此,通过构造一个平滑的连续函数逼近这个不连续的函数(即SL0范数)。
通常选用标准高斯函数
(1)
式中参数σ决定该函数逼近效果。定义向量函数
(2)
式中K是向量维数。由式(1)和式(2)可知,当σ取值较小时,则向量s的L0范数近似为‖s‖0≈K-Fσ(s)。因此,可通过下式来优化L0范数解
maxFσ(s) s.t.As=x
(3)
满足上式的参数Fσ要取最小值,当σ>0时上述连续函数与L0范数最接近。所以在σ取最小值的情况下通过Fσ(s)最大化得到SL0范数最小的解。参数σ的值决定了函数Fσ的光滑程度,σ值越大,Fσ越光滑,且局部极值较少,可很容易地实现它的最大化,但缺点是不能很好地逼近最优解; 相反地,σ值越小,逼近最优解的效果越好,但是σ取值太小,Fσ高度不平滑,导致包含大量局部最大值,很难实现Fσ的最大化。因此提出在算法中动态调整参数σ的策略。选取一个σ的递减序列{σ1,σ2,…,σJ}(其中J为递减序列元素个数),对每一个σ的值都用最速下降法不断逼近目标函数,求得Fσ的最大值。由于σ的变化幅度不是很大,每次计算得到Fσ的最优解都与上一次得到的最优解很接近,这样就能避免陷入局部最大值问题,从而得到σ值很小时Fσ的最大值,最终求得使SL0范数最小的解。
2.2 SL0范数约束的Radon变换
抛物Radon变换在时域定义为
(4)
式中:d(t,x)为时域地震数据;x为炮检距;m(τ,q)为Radon域数据;q为曲率参数;τ为截距时间。通过傅里叶变换将式(4)变到频率域,其表达式为
(5)
式中:M(ω,q)和D(ω,x)分别是m(τ,q)和d(t,x)的傅里叶变换;ω为频率;N为q的取值个数。写成矩阵形式为
d=Lm
(6)
式中L为Radon算子。
由上式可知,Radon变换其实就是求解方程组d=Lm的过程,可采用L1范数的优化问题求该方程组的稀疏解。L1范数稀疏方法虽收敛性较好,但只是L0范数的凸逼近形式,L0范数才是最能体现数据稀疏的方法。故将Radon变换求稀疏解问题转化为基于SL0范数的稀疏优化问题,其数学模型为
min‖m‖0 s.t.Lm=d
(7)
根据SL0范数的基本定义,选取高斯函数作为平滑连续函数来逼近L0范数,可得
‖m‖0≈N-Fσ(m)
对式(7)的优化问题可采用最速下降法和梯度投影原理求解,其中最速下降法是由迭代形式

构成的。随着σ的减小,μk值也应减小。这是因为σ越小,函数Fσ的“波动”越大,因此最大化Fσ要用小步长[20]。通过改变σ值观察不同尺度下的相同曲线,其中尺度是与σ成比例的,不难发现μk与σ2是成正比的。因此令μk=μσ2,其中μ是一个常数,其值通过经验设定,由此得到

式中

为梯度方向,它是通过对函数
求导得到。利用该梯度方向搜索最优值,直至得到Fσ(m)的最优解,即L0范数的最小量。
参数σ的取值非常重要,关系到最优值的搜索方向,当σ取值足够大时,满足
的最优解就是Lm=d的最小L2范数解。下面利用拉格朗日乘数法验证该观点。
设拉格朗日函数L(m,λ)=Fσ(m)-λT(Lm-d),分别对m和λ(拉格朗日乘数)求导,并令其导数都等于零,可得
(8)
定义式中λ1=-σ2λ。另外,Lm=d的最小L2范数解可用最小化
求解。利用拉格朗日乘数法,最小化结果可表示为
(9)
比较式(8)和式(9),可以发现当σ→∞ (或σ≫max{m1,…,mN})时,这两个方程组是相等的。此时使Fσ(m)最大的最优解就是Lm=d的最小L2范数解。所以用Lm=d的最小L2范数解作为算法的初始值,是优化算法的最好选择。
综上所述,基于SL0范数稀疏约束Radon变换的具体算法分如下四步。
1.对某数据d,设置初值m0为最小二乘解;
2.选取一个合适的σ递减序列[σ1,σ2,…,σJ];
3.对于每一个σ的取值都做如下处理:
令σ=σj(j=1,2,…,J),在解空间M={m|Lm=d}中,利用最速下降法迭代C次使函数Fσ(m)最大化,然后将得到的新的m值投影到解空间M中,具体步骤如下:
(1)令m=mi-1
(2)对于l=1,…,C

2)更新Radon变换的值m←m-μδ
3)采用梯度投影原理可得m←m-(LHL+μI)-1LH(Lm-d)
(3)mi=m
4.经过以上迭代循环,最终得到Radon域的数据m=mJ。
在地震数据完整的情况下,数据经过抛物Radon变换后会在Radon域聚焦得很好。但是,当地震数据缺失、有空道存在时,经过抛物Radon变换得到Radon域的数据能量比较发散,利用抛物Radon变换实现缺失地震数据重构的方法,实际上就是通过正反抛物Radon变换的多次迭代,使Radon域上的能量重新得到收敛,以恢复时域上的地震同相轴,达到地震数据重构的目的。
稀疏重构问题实际上就是如何求解欠定方程组的最稀疏解。在缺失地震数据重构中,利用L0范数稀疏约束Radon变换来求解Radon域的稀疏解,增强了地震同相轴在Radon域的收敛特性[6],保持了地震同相轴在时域的连续性,从而提高了地震数据重构的精度。
3 理论模型与实际数据处理
3.1 理论模型
为了证明本文算法的可行性和有效性,以地震数据重建为例对比基于L1范数的高分辨率Radon变换和SL0Radon变换性能。构建了两个理论模型进行实验。第一个模型如图1所示,图1a是由主频为30Hz的Ricker子波合成的地震记录,共64道,道间距为10m,每道采样点数为200,采样间隔为4ms,随着炮检距的改变3个同相轴的振幅不发生变化。图1b为均匀缺失模型,其中每隔两道抽取一道作为缺失待重建的数据。图1c和图1d分别为高分辨率Radon变换和SL0范数约束的Radon变换方法重构的结果,图1e和图1f分别为它们所对应的重构数据误差剖面图,从图中可清楚地看到SL0范数约束的Radon变换方法将三个同相轴恢复的很好,而高分辨率Radon变换方法重构数据残差中仍然有同相轴部分信息残留下来。
图2a为模型一的合成地震记录的理想Radon谱,图2b为高分辨率Radon变换谱,图2c为SL0范数约束的Radon变换谱,图2d为高分辨率Radon变换谱残差,图2e为SL0范数约束Radon变换谱残差,通过对比可看出SL0范数约束的Radon变换方法比高分辨率Radon变换方法的的分辨率更高,聚焦效果更好。
该地震数据f-k谱如图3a所示。图3b是其均匀缺失地震数据f-k谱,与原始数据f-k谱(图3a)相比,发现数据缺失后出现了明显假频现象。图3c和图3d分别是高分辨率及SL0两种方法对应的f-k谱;图3e和图3f是对应两种方法重建数据f-k谱分别与真实频谱之间的误差,可看出高分辨率Radon变换方法在重构过程中有能量丢失,这与图1e中残留的同相轴信息相对应,而SL0范数约束的Radon变换方法在保留原始数据能量的同时,还压制了假频,重构效果明显优于高分辨Radon变换。
图4a是模型二地震合成记录,其子波主频为30Hz,共64道,其中道间距为10m,每道采样点300个,采样间隔为4ms,三个同相轴的振幅随着炮检距的改变而改变。图4b是图4a中数据随机缺失26道所得的缺失数据。图4c和图4d分别为高分辨率Radon变换及SL0范数约束的Radon变换重构结果,图4e和图4f分别为其所对应的误差剖面,通过误差可看出高分辨率Radon变换方法的重构结果,不管是在近炮检距还是在远炮检距,都有同相轴信息的丢失,而SL0范数约束的Radon变换方法重构结果更精确,数据的AVO特性恢复较好。
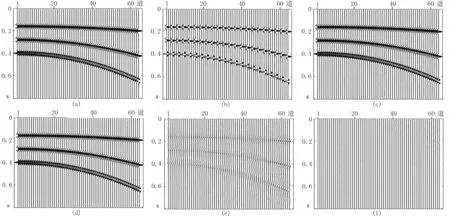
图1 振幅不变的均匀缺失数据重构模型 (a)原始地震数据; (b)均匀缺失数据; (c)高分辨率方法重构结果; (d)SL0 Radon变换方法重构结果; (e)高分辨率方法误差剖面(放大5倍); (f)SL0 Radon变换方法误差剖面(放大5倍)
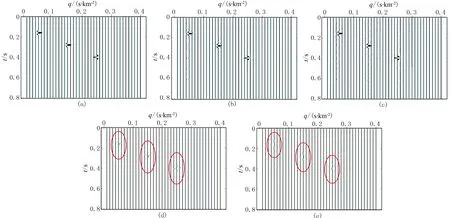
图2 振幅不变均匀缺失时两种Radon变换方法的Radon谱 (a)合成记录理想Radon谱; (b)高分辨率Radon变换谱; (c)SL0范数约束Radon 变换谱; (d)高分辨率Radon变换谱误差; (e)SL0范数约束Radon变换谱误差

图3 振幅不变的均匀缺失数据重建f-k谱比较 (a)原始数据f-k谱; (b)缺失数据f-k谱; (c)高分辨率方法重建数据f-k谱; (d)SL0 Radon变换方法重建数据f-k谱; (e)高分辨率方法重建数据f-k谱误差(放大十倍); (f)SL0 Radon变换方法重建数据f-k谱误差(放大十倍)
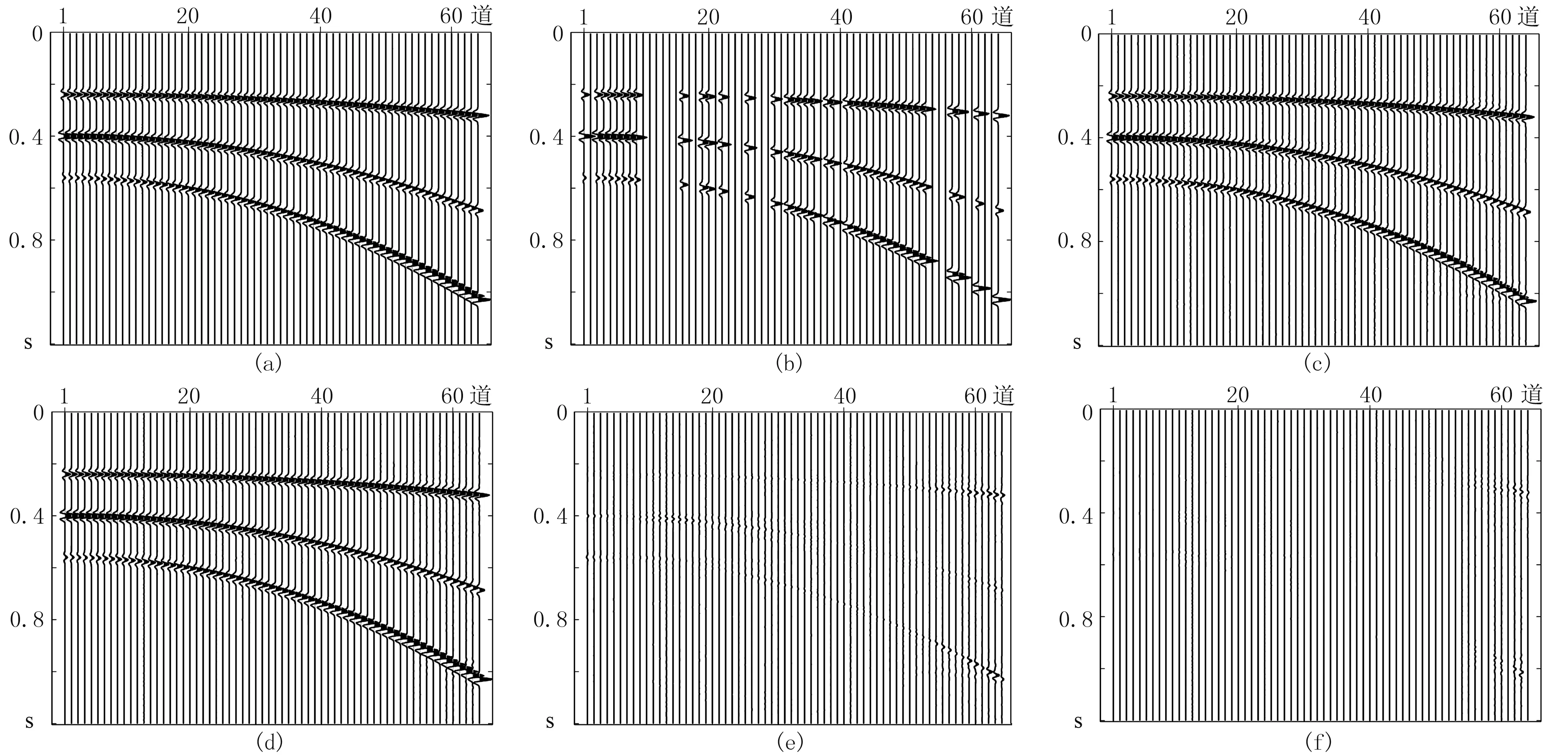
图4 振幅变化的随机缺失数据重构模型 (a)原始数据; (b)随机缺失数据; (c)高分辨率方法重构结果; (d)SL0 Radon变换方法重构结果; (e)高分辨率方法重构误差剖面; (f)SL0 Radon变换方法重构误差剖面
3.2 实际数据
图 5a为实际地震数据,共有92道,每道取401个采样点,采样间隔为4ms(来自SeismicLab软件包,http://www-geo.phys.ualberta.ca/saig/SeismicLab)。将该地震数据随机缺失32道作为缺失数据,如图5b所示。高分辨率 Radon变换及SL0范数约束的Radon变换方法重构结果分别如图5c和图5d所示。图5e和5f分别为高分辨率Radon变换和SL0范数约束的Radon变换方法重构结果与实际数据的误差剖面,通过比较可看出,SL0范数约束的Radon变换在重构时误差较小,较好地保持了地震同相轴的连续性,恢复了数据的AVO特性。
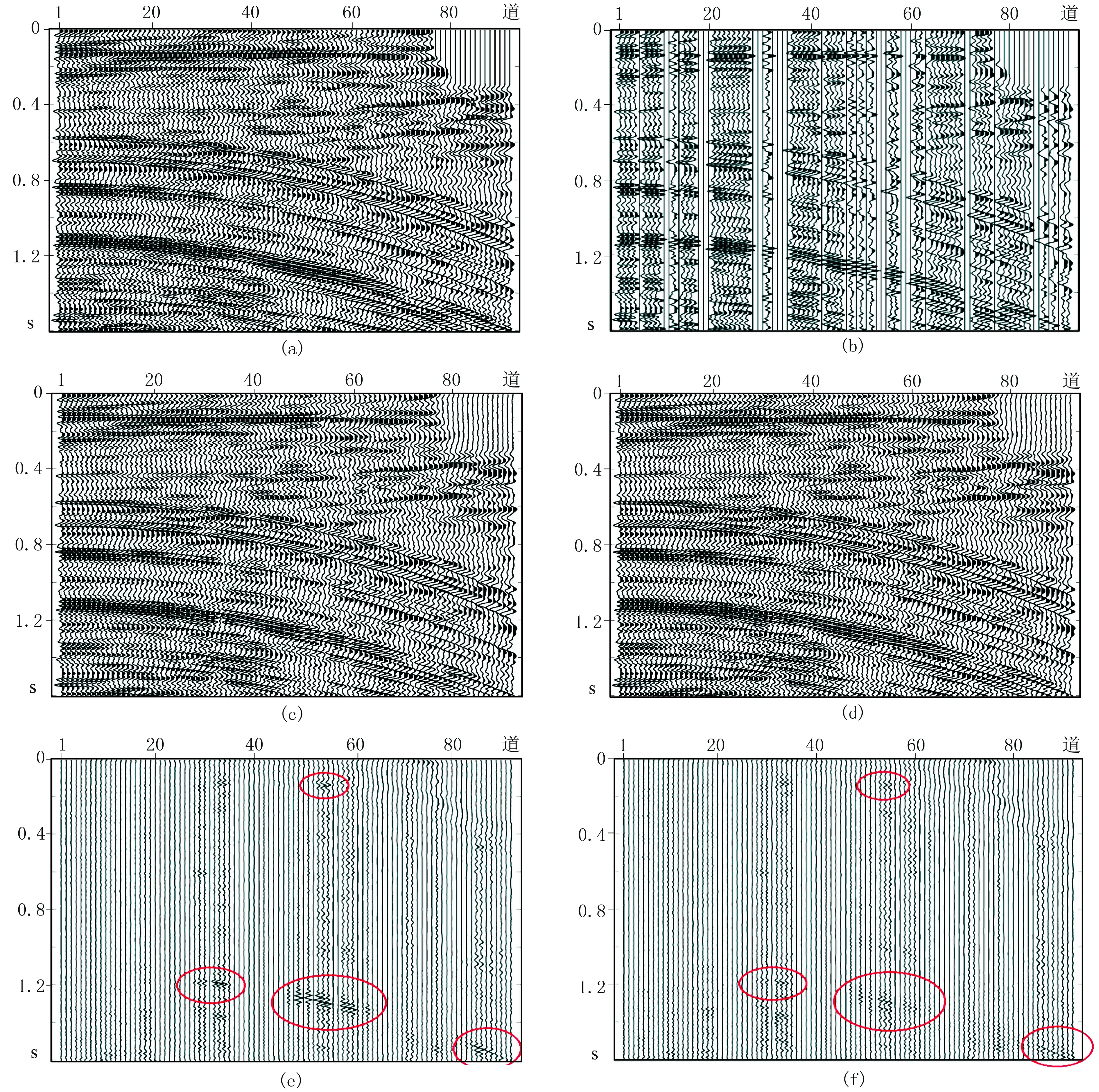
图5 实际数据随机缺失重构 (a)原始数据; (b)随机缺失数据; (c)高分辨率方法重构结果 ;(d)SL0 Radon 变换方法重构结果; (e)高分辨率方法重构误差; (f)SL0 Radon变换重构误差
4 结论
Cauchy准则和L1范数对数据的稀疏都存在局限性,它们不能充分反映数据稀疏特征,L0范数是表征数据稀疏度的最好方法,本文将L0范数稀疏约束应用于Radon变换,提出SL0范数约束的Radon变换方法。该方法比高分辨率Radon变换法的分辨率更高,压制假频效果更好。在该方法中参数σ取值决定了SL0范数的稀疏度,σ越大,稀疏度越小,Radon变换分辨率越低;σ越小,稀疏度越大,Radon变换分辨率越高,聚焦效果越好。所以在实际应用中要适当选取σ值,来提高Radon变换的效果。
地震道缺失重构问题对地震数据处理意义重大。将该方法应用于地震数据重构中,通过理论模型实验和实际地震资料处理,表明相比高分辨率Radon变换方法,该方法通过SL0范数稀疏约束Radon变换更能提高Radon变换的分辨率,更好地保持地震同相轴的连续性和恢复地震数据的AVO特性,对于不同的缺失数据都有更好的重构效果。
[1] 王雄文,王华忠.基于压缩感知的高分辨率平面波分解方法研究.地球物理学报,2014,57(9):2946-2960. Wang Xiongwen,Wang Huazhong.A research of high-resolution plane-wave decomposition based on compressed sensing.Chinese Journal of Geophysics,2014,57(9):2946-2960.
[2] 徐彦凯,曹思远,何元.双曲Radon-ASVD 方法压制叠前地震数据随机噪声.石油地球物理勘探,2017,52(3):451-457. Xu Yankai,Cao Siyuan,He Yuan.Hyperbolic Radon-ASVD method for suppressing random noise of pre-stack seismic data.OGP,2017,52(3):451-457.
[3] 薛亚茹,唐欢欢,陈小宏.高阶高分辨率Radon变换地震数据重建方法.石油地球物理勘探,2014,49(1):95-100,131. Xue Yaru,Tang Huanhuan,Chen Xiaohong.Reconstruction method of seismic data using high-order high resolution Radon transform.OGP,2014,49(1):95-100,131.
[4] 范景文,李振春,宋翔宇等.各向异性高分辨率Radon变换压制多次波.石油地球物理勘探,2016,51(4):665-669. Fan Jingwen,Li Zhenchun,Song Xiangyu et al.Suppression of multiple waves by anisotropic high resolution Radon transform.OGP,2016,51(4):665-669.
[5] 谢俊法,孙成禹,韩文功.迭代抛物Radon变换法分离一次波与多次波.石油地球物理勘探,2014,49(1):76-81. Xie Junfa,Sun Chengyu,Han Wengong.Separation of primary and multiple waves by iterative parabolic Radon transform.OGP,2014,49(1):76-81.
[6] 刘喜武,刘洪,李幼铭.高分辨率Radon变换方法及其在地震信号处理中的应用.地球物理学进展,2004,19(1):8-15. Liu Xiwu,Liu Hong,Li Youming.High resolution radon transform and its application in seismic signal processing.Progress in Geophysics,2004,19(1):8-15.
[7] 安鹏.基于高分辨率Radon变换的波场分离方法研究[学位论文].山东东营:中国石油大学(华东),2009. An Peng.Wave Field Separation Technology Research Based on High-resolution Radon Transform [D].China University of Petroleum(East China),Dongying,Shandong,2009.
[8] Sacchi M,Ulrych T.High resolution velocity gathers and offset space reconstruction.Geophysics,1995,60(4):1169-1177.
[9] Sacchi M,Porsani M.Fast high resolution parabolic Radon transform.SEG Technical Program Expanded Abstracts,1999,18:1477-1480.
[10] Trad D,Ulrych T,Sacchi M.Latest view of the sparse Radon transform.Geophysics,2003,68(1):386-399.
[11] Figueiredo M A T,Nowak R D,Wright S J.Gradient projection for sparse reconstruction:application to compressed sensing and other inverse problems.IEEE Journal of Selected Topics in Signal Processing,2007,1(4):586-597.
[12] Chen S S,Donoho D L,Saunders M A.Atomic decomposition by basis pursuit.SIAM Journal of Scientific Computing,1998,20(1):33-61.
[13] Mohimani H,Babaie-Zadeh M and Jutten C.Fast sparse representation using smoothed L0norm.IEEE Tran-sactions on Signal Processing,2007,46(6):1-12.
[14] Mohimani H,Babaie-Zadeh M,Jutten C.A fast ap-proach for overcomplete sparse decomposition based on smoothed L0norm.IEEE Transactions on Signal Processing,2009,57(1):289-301.
[15] Hyder M M and Mahata K.An improved smoothed L0approximation algorithm for sparse representation.IEEE Transactions on Signal Processing,2010,58(4):2194-2205.
[16] Zayyani H,Babaie-Zadeh M.Thresholded smoothed-L0dictionary learning for sparse representations.IEEE International Conference on Acoustics,Speech and Signal Processing,2009,1825-1828.
[17] Ghalehjegh S H,Babaie-Zadeh M,Jutten C.Fast block-sparse decomposition based on SL0.9th International Conference on Latent Variable Analysis and Signal Separation,2010,426-433.
[18] 林婉娟,赵瑞珍,李浩.用于压缩感知信号重建的NSL0算法.新型工业化,2011,1(7):78-84. Lin Wanjuan,Zhao Ruizhen,Li Hao.The NSL0algorithm for compressive sensing signal reconstruction.Industrialization,2011,1(7):78-84.
[19] 祁锐,李宏伟,张玉洁.基于改进光滑L0范数的块稀疏信号重构算法.计算机工程,2015,41(11):294-298. Qi Rui,Li Hongwei,Zhang Yujie.Block sparse signal reconstruction algorithm based on improved smoothed L0norm.Computer Engineering,2015,41(11):294-298.
[20] 杨良龙,赵生妹,郑宝玉等.基于SL0压缩感知信号重建的改进算法.信号处理,2012,28(6):834-841. Yang Lianglong,Zhao Shengmei,Zheng Baoyu et al.The improved reconstruction algorithm for compressive sensing on SL0.Signal Processing,2012,28(6):834-841.
[21] 曹静杰,王彦飞,杨长春.地震数据压缩重构的正则化与零范数稀疏最优化方法.地球物理学报,2012,55(2):596-607. Cao Jingjie,Wang Yanfei,Yang Changchun.Seismic data restoration based on compressive sensing using the regularization and zero-norm sparse optimization.Chinese Journal of Geophysics,2012,55(2):596-607.
[22] 张良,韩立国,刘争光等.基于压缩感知和Contourlet变换的地震数据重建方法.石油物探,2017,56(6):804-811. Zhang Liang,Han Liguo,Liu Zhengguang et al.Seismic data reconstruction based on compressed sending and Contourlet transform.GPP,2017,56(6):804-811.

