一种修正的Kuster-Toksöz岩石物理模型及应用

刘致水 孙赞东 董 宁 刘俊州 刘致秀 王亚静

(①长安大学地质工程与测绘学院，陕西西安 710054； ②中国石油大学(北京)，北京 102249； ③中国石化石油勘探开发研究院，北京100083； ④中国石油东方地球物理公司，河北涿州 072751； ⑤庆阳职业技术学院，甘肃庆阳 745000)

1 引言

岩石物理模型是描述弹性参数与储层特征之间关系的数学函数[1-3]。针对不同的地质目标和问题，前人提出了多种岩石物理理论和模型，包括基础理论[2-7]，针对碎屑岩[8-12]、碳酸盐岩[13-18]、页岩[19-22]等的应用模型；其中Kuster-Toksöz(KT)模型[4]、微分等效介质模型[2，3](DEM)比较经典，应用广泛。KT模型能够同时考虑多种具有不同形状的包含物对弹性参数的影响，其中不同包含物之间的关系平等；它的缺点是认为岩石中的包含物是“稀疏”存在的，也就是包含物含量不能太高[6-8，14，15]。DEM模型通过将包含物微分并多次加入岩石基质中，从而不受“稀疏”含量包含物的限制。但是DEM模型只能考虑单一包含物类型，在处理多种类型包含物岩石的问题时，只能多次重复使用DEM公式[14]，且计算结果依赖于包含物的添加顺序[1]。

针对上述问题，Kuster等[4]、Xu等[8]分别提出用微分等效的思想通过“迭代”的方式实现模拟，但是他们并未给出相应的公式。尤其需要注意的是，这种模拟不是简单地用KT公式迭代就可以得到真实值，在迭代过程中由于物质的替换，参与计算的包含物含量和真实的包含物含量数值是不同的，如果仅仅用KT公式迭代计算，则得到的结果必然是错误的。李宏兵等[6]基于KT模型推导了一种微分格式的微分等效多孔隙岩石物理模型，进而得到了相应的解析公式，但是其微分格式与DEM格式一致，计算过程中需要求解微分方程；且解析公式是针对空孔隙的，不能应用于包含物体积模量和剪切模量不为零的情况，即不能用于计算固体包含物的情况，这极大地缩小了模型的应用范围，例如该模型不能将有机质颗粒(干酪根)作为包含物考虑，从而使其很难应用于富有机质岩石。在富有机质岩石中，干酪根的体积模量和剪切模量都较小[1,20]。一些学者[19-22]在构建富有机质岩石的岩石物理模型时将干酪根等效为固体颗粒，使用包含物模型表征干酪根对岩石速度的影响，这就需要能够同时考虑多种不同形状的固体和流体包含物、又不受“稀疏”含量包含物的限制的岩石物理模型。针对速度预测，Xu等[8]在KT模型基础上，将岩石中的孔隙分为泥质孔隙和砂质孔隙，提高了速度预测的精度，但是假设泥质孔隙、砂质孔隙与岩石中的泥岩和砂岩含量成正比，这种假设在大多数情况下是没有根据的。Xu等[15]针对碳酸盐岩，将岩石中的孔隙细分为泥质孔隙、印模孔、粒间孔、微裂隙，使用这种复杂的孔隙类型进行速度预测得到较好的效果，但是每种孔隙在孔隙度中的体积分数很难准确求取，使该方法缺乏严谨的数学基础。

本文将微分等效思维引入KT岩石物理模型，得到一个适用于高浓度包含物的修正Kuster-Toksöz岩石物理模型，并给出了计算过程中所使用的“计算包含物体积含量”与岩石中真实包含物体积含量之间的数学关系。利用所建立的新岩石物理模型，构建了考虑干酪根与孔隙两种包含物的富有机质岩石速度预测流程，其中干酪根分为球形颗粒与硬币状颗粒，两种颗粒之比固定；包含流体孔隙分为球形孔隙与硬币状孔隙，计算过程中两种孔隙类型的体积比可变(自适应)，在纵波速度的约束下可求得孔隙类型的含量，最后通过孔隙类型体积比求取横波速度。

2 基本原理

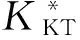
(1)

(2)

(3)

(4)

硬币状裂缝孔隙或包含物的形状因子为

(5)

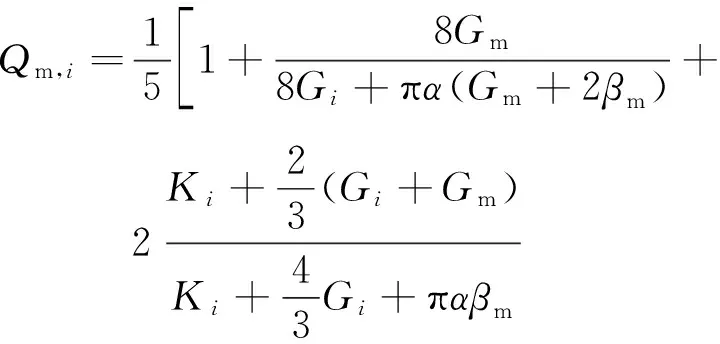
(6)

在KT模型中，假设包含物随机分布，以使其等效为各向同性。通过把包含物模量设为零模拟干岩石，把包含物的剪切模量设为零模拟流体饱和岩石。

KT模型有两个限制条件： 其一为模拟的是高频条件下饱和岩石的属性，适用于超声实验室条件； 其二为要求包含物是“稀疏”的，也就是包含物体积含量不能太大。对于第一个限制，公认且有效的做法是通过引入Gassmann方程[23]以得到低频条件下的岩石弹性模量[14]； 对于第二个限制，本文引入微分等效的思想，其基本过程(图1)为： 将包含物划分为N小份(极小量)，分为N次加入岩石基质中，每一小量代表不同的成分与形状，每次加入后包含物相替代同体积分数的基质相，从而形成混合相，将这个混合相作为新的基质相以进行下一次迭代，重复N次直到加入的包含物相体积分数达到真实值。

式(1)和式(2)可以被重写为

(7)

(8)

图1 多种包含物微分等效介质岩石物理模型的等效过程示意图

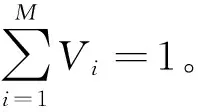
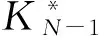
(9)

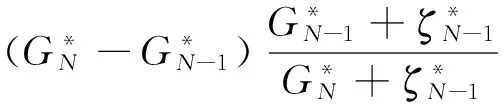
(10)

进而可写为

(11)

(12)

每次迭代都可以看作使用小量的包含物替代岩石背景基质，迭代完成后，包含物随机分散在岩石基质中。除第一次迭代外，新加入的包含物所替代的不只是岩石基质，也有包含物的一部分，而本质上新加入包含物需要替代的物质只能是岩石基质。因此，每次加入基质中的包含物y不是真实的包含物体积含量分量(dVt)，仅有(1-Vt)y对迭代过程中的真实包含物体积含量分量dVt有贡献，即每次迭代过程中的真实包含物体积含量的变化量为

dVt=(1-Vt)y

(13)

那么，岩石中的真实包含物体积含量与y之间的关系为

Vt=1-e-∑y

(14)

式中∑y称为“计算包含物体积含量”。如果迭代次数为N，那么上式为

Vt=1-e-Ny

(15)

此时，“计算包含物体积含量”为Ny，y可写为

(16)

图2为真实包含物体积含量(Vt)与“计算包含物体积含量(Ny)”之间的关系曲线。由图可见，当包含物含量小于0.1时，两者差距较小；随着真实包含物体积含量的增大，所需要的计算包含物体积含量数值越大。

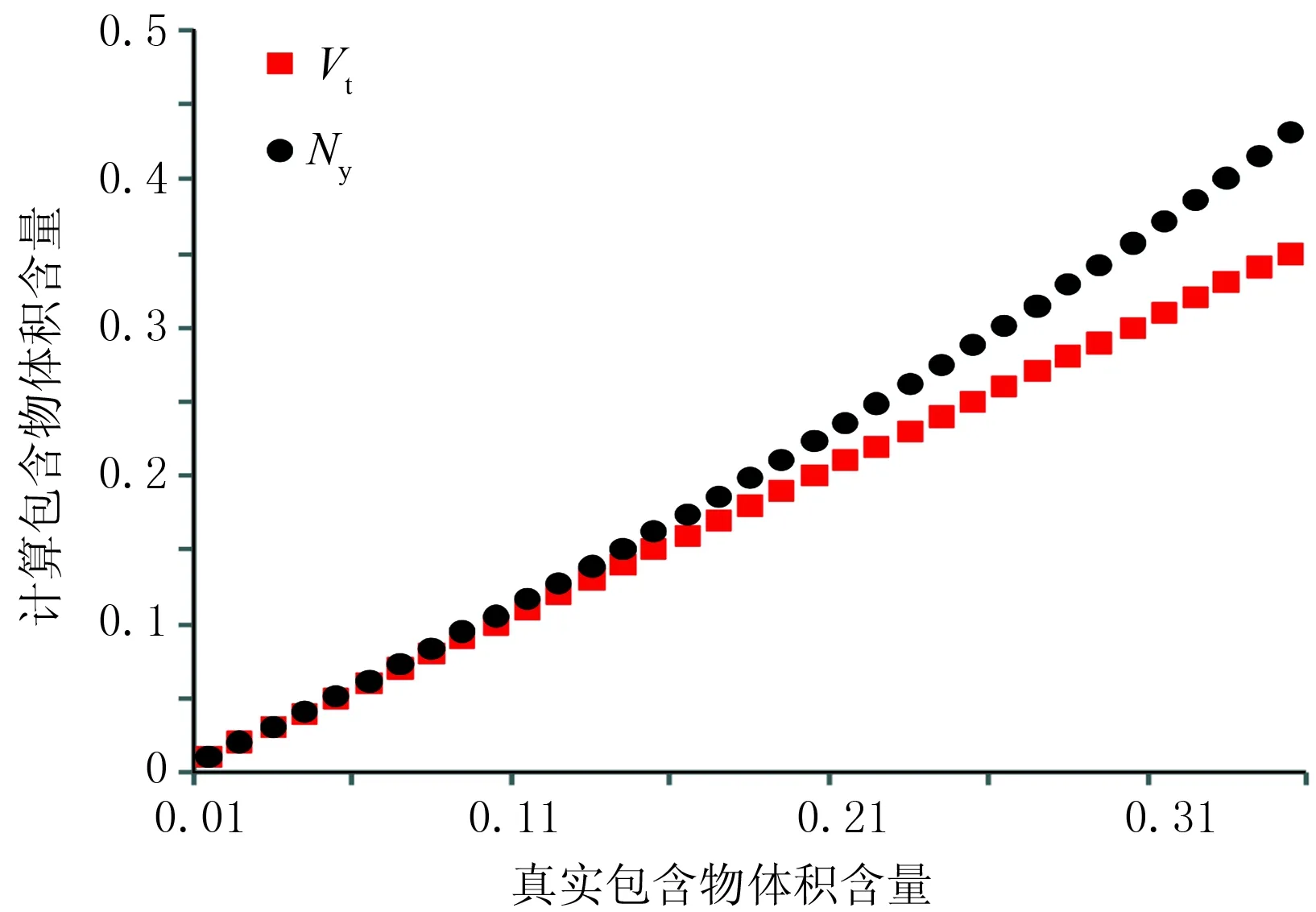
图2 真实包含物与计算包含物体积含量关系曲线

表1 不同孔隙度与孔隙形状条件下体积模 量计算精度达到0.001所需迭代次数

表2 不同孔隙度与孔隙形状条件下剪切模 量计算精度达到0.001所需迭代次数

3 模型对比分析

使用两组数值进行计算，对比新模型与KT模型之间的差别。

第一组：往砂岩基质孔隙中加入气体，其中砂岩基质体积模量为37GPa，剪切模量为44GPa；孔隙流体的体积模量Kf为0.01GPa；分别对球形孔、硬币状裂缝孔隙进行模拟，硬币状裂缝的孔隙纵横比分别设为0.01、0.05、0.70、1.00，此时式(9)～式(12)中M=1，式(16)中真实包含物体积含量为孔隙度φ； 数值模拟中假设孔隙度为0～100%，需要注意的是，真实岩石中的孔隙度不能大于临界孔隙度[5]。数值模拟结果如图3所示：当孔隙度较小时，新模型与KT模型一致，例如针对孔隙纵横比为0.01的硬币状裂缝孔隙，在孔隙度小于5%时两者基本一致；随着孔隙度增大，新模型与KT模型的差距变大，与KT模型相比，新模型在高孔隙度时可以得到更合理的值。一种极端情况是当孔隙度为100%时，真实值应该是孔隙包含物的参数，新模型可以得到真实值，而KT模型所计算的结果不等于包含物的参数，这显然是不对的。

第二组：往页岩基质中加入干酪根颗粒，页岩基质体积模量为39.54GPa，剪切模量为25.68GPa;干酪根颗粒体积模量为2.9GPa，剪切模量为2.7GPa[1]；分别对球形颗粒、硬币状颗粒进行模拟，硬币状颗粒的纵横比分别为0.01、0.05、0.70、1.00，此时式(9)～式(12)中M=1，式(16)中Vt是干酪根体积含量；数值模拟中假设干酪根体积含量为0～100%。数值模拟结果如图4所示，其结果与图3一致。

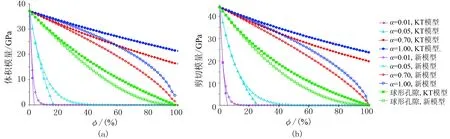
图3 不同孔隙形状时KT模型与新模型正演结果对比 (a)体积模量； (b)剪切模量

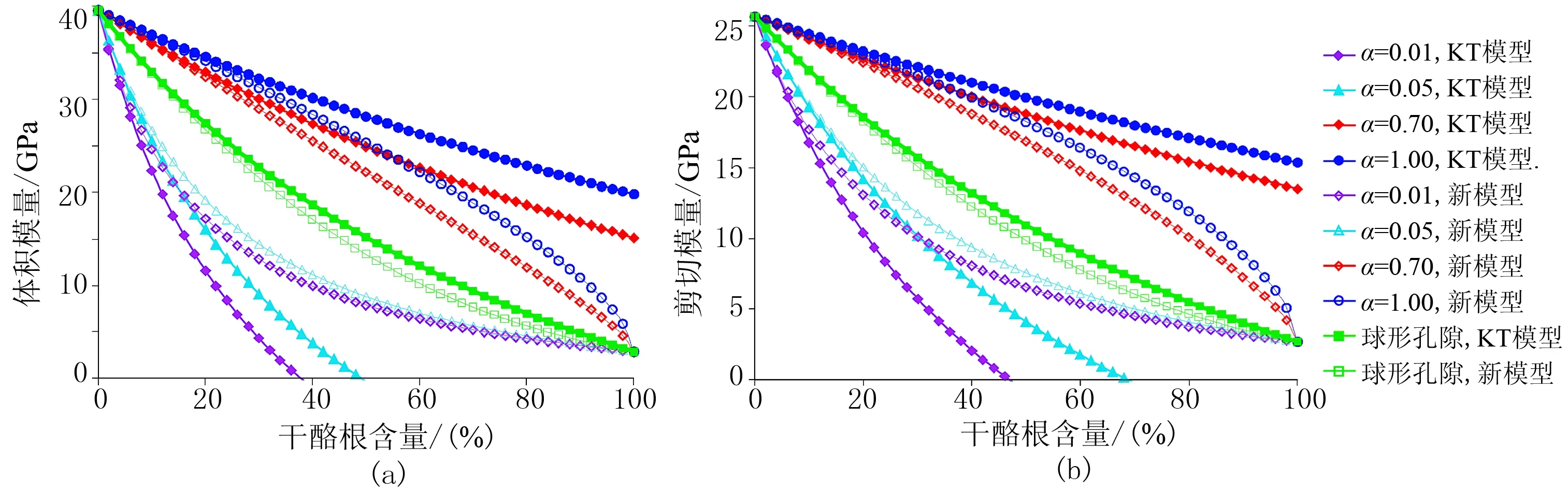
图4 不同干酪根颗粒形状时KT模型与新模型正演结果对比 (a)体积模量； (b)剪切模量

4 模型在富有机质岩石中的应用

富有机质岩石的成分包括矿物、干酪根、饱和流体孔隙。干酪根的物理参数较为特殊，如表3所示：干酪根的体积模量、密度与石英、方解石、黏土等矿物相差较大，与水接近；但是它具有剪切模量，又与流体不同。本文将干酪根等效为岩石中的一种包含物，与饱和流体孔隙一同加入岩石基质中，从而进行富有机质岩石的速度预测。

利用Vernik等[24]在超声实验室针对干岩石测量的数据(70MPa围压环境)说明干酪根、孔隙对富有机质岩石速度的影响并测试新模型。本文使用了其测量的59个干岩石样品数据中的51个，未使用纵、横波速度较高的8个样品。所使用的51个样品的干酪根含量为1.4%～42.3%，孔隙度为0.6%～30.9%。图5是样品的纵波速度、横波速度与孔隙度、干酪根含量交会图。由图可见：在干酪根含量近似不变时(例如深蓝色时)，随着孔隙度的增加，岩石的纵、横波速度整体呈减小趋势；在孔隙度近似不变时(例如孔隙度接近0)，可非常明显地看到随干酪根含量的增加，岩石的纵、横波速度减小。此外，纵、横波速度数据点较分散，例如图中用直线段标注的五个数据点，其孔隙度近10.0%，而纵波速度在3.2～5.1km/s范围内变化，横波速度在2.1km/s～3.1km/s范围内变化，本文认为这种速度分散是由孔隙形状及干酪根颗粒形状的变化所引起。

表3 岩石组成成分的弹性参数和密度[1]

Xu等[8]将孔隙分为柔性孔隙与刚性孔隙，使用Wu[25]的椭球体模型表征孔隙类型(孔隙纵横比的大小表征孔隙的形状)，其中刚性孔隙的孔隙纵横比为0.12～0.15，柔性孔隙的孔隙纵横比为0.02～0.03。刚性孔隙与柔性孔隙的体积比与岩石中砂岩/泥岩体积比一致。本文将页岩中的干酪根和孔隙等效为具有一定形状的包含物，其中干酪根体积含量(Vk)等效为由刚性颗粒(Vks)与柔性颗粒(Vkc)组成，将孔隙度(φ)等效为由刚性孔隙度φs与柔性孔隙度φc组成，其中刚性颗粒和孔隙使用多种孔隙理论[1]中的球型包含物表征，柔性颗粒和孔隙使用硬币形状包含物表征(颗粒及孔隙纵横比取0.02)。理论上通过新模型可以考虑多种包含物及孔隙类型，但是难点为需要知道每种类型包含物各自的体积分数。

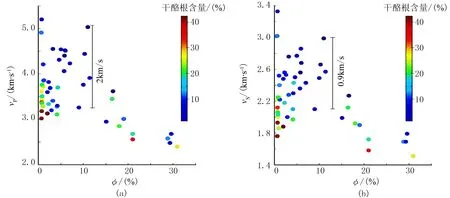
图5 富有机质岩石的纵波速度(a)、横波速度(b)与孔隙度、干酪根含量的交会图(数据来自文献[24])

由图5可见，干酪根含量较高(暖色表征)时，纵波与横波速度的分散性较低，因此假定速度分散主要由孔隙形状的变化引起，在计算中固定刚性干酪根颗粒Vks与柔性干酪根颗粒Vkc的比例，而刚性孔隙与柔性孔隙的体积比是可变(自适应)的。经过多次试算并求取预测值相对于实际值的均方根误差(RMSE)，本文最终选择刚性干酪根颗粒与柔性干酪根颗粒的比例为1∶1。图6为纵、横波的均方根误差随刚性干酪根颗粒在干酪根总量中的占比Vks的变化(间隔为-0.05)。由图6可见，在1～0之间，纵波的RMSE有两个极小值：当Vks=0.75时纵波的均方根误差为0.0606km/s，其所对应的横波均方根误差为0.0812km/s；当Vks=0.5时纵波的均方根误差为0.0607km/s，其所对应的横波均方根误差为0.0772km/s。因此本文选择Vks=0.5(即刚性干酪根颗粒与柔性干酪根颗粒相等)进行计算。

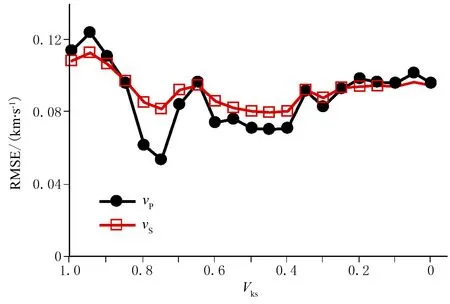
图6 纵、横波速度的均方根误差随刚性 干酪根颗粒的体积比Vks的变化

此时，式(15)中Vt指孔隙度φ与干酪根体积含量Vk之和；式(9)～式(12)中M=4，包含物体积分数Vi有四个：球形干酪根颗粒V1、硬币状干酪根颗粒V2、球形孔隙V3、硬币状孔隙V4，其具体表达式为

(17)

(18)

(19)

(20)

式中：Vks+Vkc=1，本文Vks、Vkc取值均为0.5；φc+φs=1，φc与φs体积比可变。

利用式(11)、式(12)、式(16)及式(17)～式(20)，将干酪根颗粒和孔隙(含流体孔隙或干孔隙)加入岩石基质中，得到体积模量K和剪切模量G，则岩石的纵波速度和横波速度可以表示为

(21)

(22)

式中ρ=ρm(1-φ-Vk)+ρfφ+ρkVk，ρm、ρk、ρf分别指岩石基质、干酪根、孔隙中流体的密度，在干岩石中ρf取为零。需要说明的是，通过上述过程得到的是超声波条件下的高频速度，要得到低频条件下的饱和流体岩石速度，则须利用式(11)～式(16)以及式(17)～式(20)获得干燥空腔的等效模量，再利用Gassmann理论往空腔中加入流体。

图7为利用上述富有机质岩石速度计算流程正演结果与实测数据的对比。由图可知：当孔隙度不变、干酪根含量增加时，岩石的速度降低；在干酪根含量不变、孔隙度增加时，岩石的速度降低；随着球形孔隙含量的降低，岩石的速度降低。通过孔隙度、干酪根含量的变化，可以覆盖所有数据点，即新模型可以解释测量数据的孔隙度—干酪根含量—速度之间的关系。

这样，就建立了纵、横波速度与可变的孔隙参数(φc、φs)之间的关系，通过使计算的纵波速度vPcal与实测的纵波速度vPmea之差达到最小来建立目标函数

ε=|vPcal-vPmea|

(23)

采用迭代算法使该式取极小值以反演得到孔隙参数(φc和φs)。计算过程中需要输入的数据包括干酪根体积含量Vk、孔隙度φ、基质体积含量1-Vk-φ； 输入的参数还包括： 页岩基质体积模量为39.54GPa、剪切模量为25.68GPa、密度为2.64g/cm3，干酪根颗粒体积模量为2.9GPa、剪切模量为2.7GPa、密度为1.3g/cm3，孔隙中气体的体积模量为0.18GPa、密度为0.26g/cm3。包含物总数M设为4，迭代次数N设为200。最终，将这些参数代入式(9)～式(16)以计算横波速度。计算过程中取ε=0.005为约束量。图8为预测纵波与实测纵波交会图，图中位于对角线上的数据点代表预测速度与实测速度之间吻合度高。由图可见，新模型与KT模型所得纵波差别较小，绝大部分数据点实测纵波速度与计算纵波速度吻合度高。有几个点的实测数据与预测数据不吻合，超出了约束量范围，其原因是所取的基质参数、干酪根颗粒的形状与该数据点的情况差别较大，孔隙度、孔隙类型、干酪根含量的变化不足以消除这种影响，说明在实际应用中，需要根据具体的研究对象选择基质参数以及干酪根颗粒形状。

图9显示了新模型和KT模型所得到的球形孔隙和硬币状孔隙在包含物中所占的体积分数。由图可见：①KT模型所得结果中球形孔隙体积分数或硬币状孔隙体积分数为零的情况多于新模型，说明KT模型在孔隙变化范围内不能达到纵波约束量的情况多于新模型，这与图8结果一致；②小孔隙岩样所得的球形孔隙体积分数或硬币状孔隙体积分数差别不大，对于大孔隙度岩样，新模型所得球形孔隙体积分数小于KT模型结果，所得硬币状孔隙体积分数略大于KT模型结果，说明新模型在刚性孔隙含量较少的情况下得到了准确的速度预测结果，这与图3、图4正演结果一致。

图10为新模型和KT模型预测横波与实测横波结果的对比。图中的点离对角线越近表明预测速度与实测速度之间的吻合度越高。显然，新模型所得预测速度与实测速度吻合度高(图10a)。

图7 基于新模型的纵波速度(a)和横波速度(b)正演结果

其中红线表示基质中加入5%的干酪根颗粒，纵、横波速度随孔隙度(0～40%，干孔隙空腔)的变化，黑线表示基质中加入40%的干酪根颗粒，纵、横波速度随孔隙度(0～40%)的变化。从上到下的六条红线和黑线分别代表球型孔隙体积比(φs)为100%、80%、60%、40%、20%、0

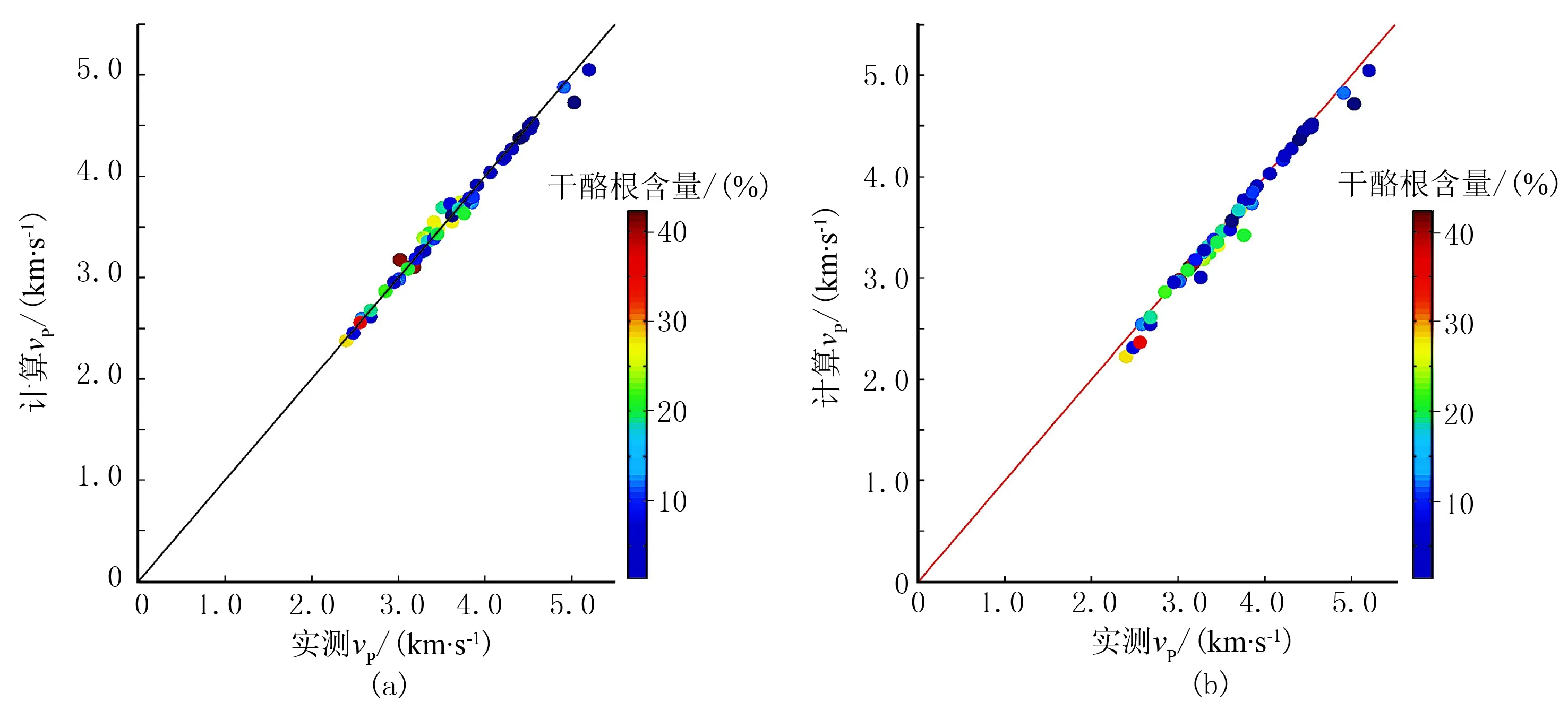
图8 纵波速度约束计算的结果与实测结果对比 (a)新模型； (b)KT模型

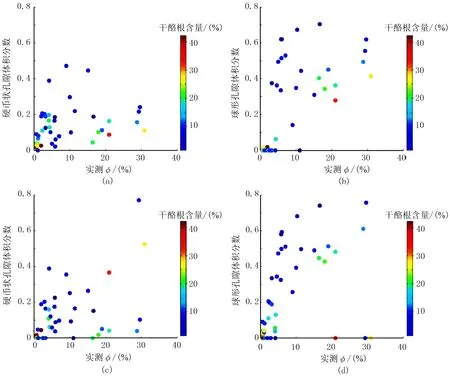
图9 新模型与KT模型计算的硬币状裂缝孔隙与球形孔隙占包含物总量的体积分数 (a)新模型硬币状孔隙； (b)新模型球形孔隙； (c)KT模型硬币状孔隙； (d)KT模型球形孔隙

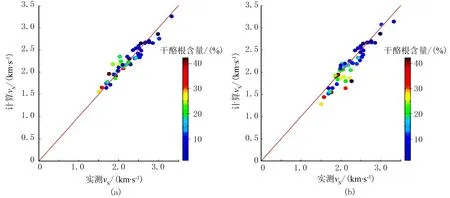
图10 预测的横波速度与实测横波速度交会图 (a)新模型； (b)KT模型

5 结论

本文将微分等效思维引入KT模型，提出了一种适用于高浓度包含物的修正Kuster -Toksöz岩石物理模型。该岩石物理模型保留了KT模型能够同时考虑多种包含物类型对弹性参数的影响的优点，又适合于高浓度包含物的情况。将该模型应用于富有机质岩石中，将孔隙和干酪根固体颗粒作为包含物同时加入岩石基质，结果证明新模型比KT模型更适合于包含物(孔隙和干酪根固体)浓度较高的情况；利用建立的岩石物理模型对实验室测试的富有机质岩石资料进行横波速度预测，干酪根颗粒采取固定比例的球形与硬币状组合，孔隙采取可变的球形与硬币形状组合，在纵波速度的约束下预测横波速度，结果证明，与KT模型相比，新模型的预测误差更小。

[1] Mavko G，Mukerji T and Dvorikin J.The Rock Phy-sics Handbook：Tools for Seismic Analysis in Porous Media.Cambridge University Press，1998.

[2] Norris A N.A differential scheme for the effective moduli of composites.Mechanics of Materials，1985，4(6)：1-16.

[3] Zimmerman R W.Compressibility of Sandstones.Elsevier，New York，1991.

[4] Kuster G and Toksöz M.Velocity and attenuation of seismic waves in two phase media.Geophysics，1974，39(5)：587-618.

[5] Nur A.Critical porosity and the seismic velocities in rocks.Eos Transactions American Geophysical Union，1992，73(1)：43-66.

[6] 李宏兵，张佳佳.多重孔岩石微分等效介质模型及其干燥情形下的解析近似式.地球物理学报，2014，57(10)：3422-3430. Li Hongbing，Zhang Jiajia.A differential effective medium model of multiple porosity rock and its analytical approximations for dry rock.Chinese Journal of Geophysics，2014，57(10)：3422-3430.

[7] 印兴耀，化世榜，宗兆云.基于线性近似的微分等效介质方程解耦方法.石油地球物理勘探，2016，51(2)：281-287. Yin Xingyao，Hua Shibang，Zong Zhaoyun.A decoupling approach for differential equivalent equations based on linear approximation.OGP，2016，51(2)：281-287.

[8] Xu S and White R E.A new velocity model for clay-sand mixtures.Geophysical Prospecting，1995，43(1)：91-118.

[9] 刘雅杰，李生杰，王永刚等.横波预测技术在苏里格气田储层预测中的应用.石油地球物理勘探，2016，51(1)：165-172. Liu Yajie，Li Shengjie，Wang Yonggang et al.Reservoir prediction based on shear wave in Sulige Gas Field.OGP，2016，51(1)：165-172.

[10] 唐杰，王浩，姚振岸等.基于岩石物理诊断的横波速度估算方法.石油地球物理勘探，2016，51(3)：537-543. Tang Jie，Wang Hao，Yao Zhen’an et al.Shear wave velocity estimation based on rock physics diagnosis.OGP，2016，51(3)：537-543.

[11] 侯波，陈小宏，张孝珍等.临界孔隙度Pride模型及其应用.石油地球物理勘探，2012，47(2)：277-281. Hou Bo，Chen Xiaohong，Zhang Xiaozhen et al.Critical porosity Pride model and its application.OGP，2012，47(2)：277-281.

[12] 郭栋，印兴耀，吴国忱等.横波速度计算方法与应用.石油地球物理勘探，2007，42(5)：535-538. Guo Dong，Yin Xingyao，Wu Guochen et al.Computational approach of S-wave velocity and application.OGP，2007，42(5)：535-538.

[13] Sun S Z，Stretch S R and Brown R J.Comparison of borehole velocity-prediction models and estimation of fluid saturation effects：From rock physics to exploration problem.Journal of Canadian Petroleum Techno-logy，2004，43(3)：18-26.

[14] Sun S Z，Wang H Y，Liu Z S et al.The theory and application of DEM-Gassmann rock physics model for complex carbonate reservoirs.The Leading Edge，2012，31(2)：152-158.

[15] Xu S and Payne M.Modeling elastic properties in car-

bonate rocks.The Leading Edge，2009，28(1)：66-74.

[16] Wang H Y，Sun S Z，Yang H J et al.The influence of pore structure on P- and S-wave velocities in complex carbonate reservoirs with secondary storage space.Petroleum Science，2011，8(4)：394-405.

[17] 张秉铭，刘致水，刘俊州等.鄂尔多斯盆地北部复杂碳酸盐岩横波速度预测研究.石油物探，2017，56(3)：328-337. Zhang Bingming，Liu Zhishui，Liu Junzhou et al.An improved S-wave velocity prediction method for complex carbonate reservoir in North Ordos Basin，China.GPP，2017，56(3)：328-337.

[18] 张广智，李呈呈，印兴耀等.基于修正Xu-White模型的碳酸盐岩横波速度估算方法.石油地球物理勘探，2012，47(5)：717-722. Zhang Guangzhi，Li Chengcheng，Yin Xingyao et al.A shear velocity estimation method for carbonate rocks based on the improved Xu-White model.OGP，2012，47(5)：717-722.

[19] 董宁，霍志周，孙赞东等.泥页岩岩石物理建模研究.地球物理学报，2014，57(6)：1990-1998. Dong Ning，Huo Zhizhou，Sun Zandong et al.An investigation of a new rock physics model for shale.Chinese Journal of Geophysics，2014，57(6)：1990-1998.

[20] 刘致水，孙赞东.新型脆性因子及其在泥页岩储层预测中的应用.石油勘探与开发，2015，42(1)：117-124. Liu Zhishui,Sun Zandong.New brittleness indexes and their application in shale/clay gas reservoir prediction.Petroleum Exploration and Development，2015，42(1)：117-124.

[21] 胡起，陈小宏，李景叶.基于单孔隙度纵横比模型的有机页岩横波速度预测方法.地球物理学进展，2014，29(5)：2388-2394. Hu Qi，Chen Xiaohong，Li Jingye.Shear velocity prediction for organic shales based on the single aspect ratio model.Progress in Geophysics，2014，29(5)：2388-2394.

[22] Guo Z，Chapman M，Li X.A shale rock physics model and its application in the prediction of brittleness index，mineralogy，and porosity of the Barnett Shale.SEG Technical Program Expanded Abstracts，2012，31.

[23] Gassmann F.Elastic waves through a packing of spheres.Geophysics，1951，16(4)：673-685.

[24] Vernik L and Liu X Z.Velocity anisotropy in shales：a petrophysical study.Geophysics，1997，62(2)：521-532.

[25] Wu T T.The effect of inclusion shape on the elastic moduli of a two phase material.International Journal of Solids & Structures，1966，2(1)：1-8.