修正辛—准粒子法地震波数值模拟

苏 波 庹先国 刘知贵

(①中国工程物理研究院研究生院，四川绵阳 621900； ②四川理工学院，四川自贡 643002；③西南科技大学计算机科学与技术学院，四川绵阳 621010)

1 引言

地震波波动方程的直接数值求解方法需要对空间和时间进行数值离散[1]。针对空间离散，常用的方法有有限差分法(FDM)[2,3]、有限元法(FEM)[4-6]、伪谱法(PSM)[7-9]、谱元法(SEM)[10,11]和近似解析离散法(NADM)[12-14]等。近年来，基于粒子的方法作为传统基于连续波动方程求解方法的一个替代选项而被用于地震波数值模拟。Takekawa等[15]将Suzuki等[16]提出的Hamiltonian particle method(HPM)用于地震波数值模拟。

相比以上在空间离散方面的大量研究，对时间离散方面的研究相对较少[17]。时间离散在显式格式上大多采用二阶中心差分(second-order central difference，CD)，然而该算法在时间步长较大时将导致严重的数值频散，且随着大规模运算的进行，数值频散效应造成累积误差逐渐增大。考虑到隐式格式在不考虑库朗数的情况下可以取得相对较大的时间步长，罗明秋等[18]对隐式辛格式做了相关研究，但隐式算法需要求解方程组，计算量较大。Chen[19]讨论了三种高阶时间离散策略(Lax-Wendroff方法、三级四阶辛格式RKN方法和三阶分步Runge-kutta方法)，大量数值实验表明，辛算法对时间误差压制能力强于Lax-Wendroff方法。实际计算表明，二阶格式精度往往不够高[11,20]，虽然采用传统三阶、四阶辛格式提高了时间精度，但是它们具有负的辛系数，这与时间演进方向不符，正的辛系数才符合实际情况，更具有长时间稳定性[21]。

本文首先基于Hamilton力学，并借鉴分子动力学的基本原理，介绍一种简单、直观、物理意义明确的空间准粒子离散体系。然后利用Liu等[17,22]提出的构造高阶辛算法策略，也即在传统辛格式中额外加入空间算子，构造出一种新的具有时间三阶精度的辛格式，达到修正精度的目的。最后，为了测试新的辛格式和空间准粒子体系的准确性，用均匀模型的解析解与本文方法的数值解进行对比。为了测试稳定性，进一步选取Sigsbee 2B速度模型进行验证。

2 空间离散—准粒子体系

地震波的传播过程是能量逐步耗散殆尽的过程，但在实际应用中常常将其假设为无能量损耗过程[18]。冯康[23]指出，所有保守无耗散系统均可以表示成Hamilton形式。本文利用弹性波方程描述地震波传播现象，为了讨论方便，只考虑各向同性弹性介质。

2.1 Hamilton体系的线性形式

针对Hamilton体系的动力演化特性，由分子动力学及能量守恒法则，可将系统看成由N个粒子组成(图1)。

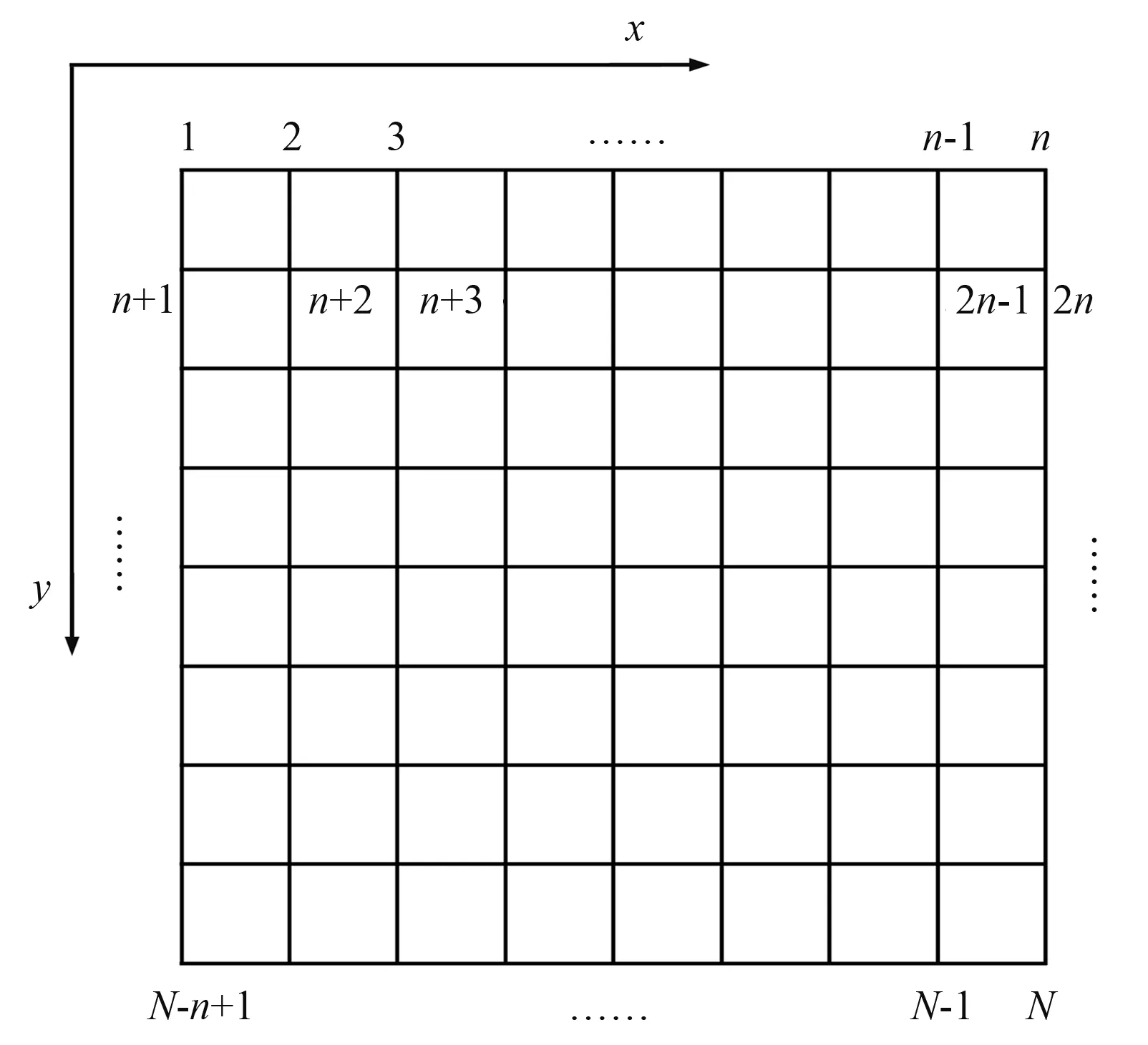
图1 准粒子体系编号规则

假设每个粒子的质量为mi，系统总能量由动能和势能构成。动能由各个质点i在x、y方向上对应的动量pxi、pyi决定；势能E由分子离开平衡位置的位移量qxi、qyi决定，Hamilton量可表示为

(1)

为简化起见，在该体系中各个粒子仅与上、下、左、右和4个对角粒子发生相互作用，且认为其作用力和相对位移呈近似线性关系。假设微观粒子具有不可辨性,体系势能在平衡位置的Taylor展开为

(2)

式中粒子在平衡位置处的势能E0为常数，E的一阶导数在平衡位置为零，而其二阶偏导数正定。令E0=0，由式(1)可以进一步得到Hamilton体系的线性形式为

(3)

式中αij、βij和γij分别表示在x、y方向的粒子间相互作用系数。

2.2 粒子间的相互作用系数

由于弹性波是矢量波，在各个方向上粒子间的相互作用关系不同，但在相同轴上对中心准粒子的作用力大小相同。准粒子间的相互作用系数为

(4)

(5)

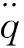
(6)

令二维网格粒子间距为d，根据连续偏导数与离散量的关系，由式(6)可得

(7)

(8)

比较。式中：u为位移；λ、μ为拉梅常数，满足以下关系

(9)

式中c0为泊松比。由式(7)～式(9)可以得到一组准粒子体系相互作用系数与P波速度vP、介质密度ρ以及泊松比c0之间的相互关系[24]

(10)

将式(10)作为空间离散系数代入式(5)，实现对波动方程的空间离散。

3 时间离散—修正辛格式

文中通过在二阶辛格式[25]的基础上构建一个新的修正辛格式，该格式具有三阶时间精度，并在理论上推导了其数值频散和稳定性。为了方便讨论，记修正辛格式为M1、二级二阶辛格式[21]为M2、三级三阶辛格式[26]为M3。

3.1 构造修正辛格式

(11)

式(11)进一步变换为Hamilton形式

(12)

其中

为了求解半离散方程组(式(12))，常用二阶方法[23]

(13)

(14)

对于式(14)可以基于Taylor原理得到三阶精度条件

(15)

3.2 稳定性分析

为了验证修正辛格式的稳定性，设在t=nΔt时刻式(8)的简谐解为

(16)

式中：ωnum为角频率；kx=kcosφ和ky=ksinφ分别为x,y方向的波数,φ为波数矢量k=(kx,ky)与x轴间的夹角。

将式(16)代入式(14)得到形如

(υn+1,un+1)T=G(υn,un)T

的时间演进方程。式中：G为增长矩阵。设G和空间算子L的特征值分别为ψ和ξ，可得G的特征多项式为

(17)

使式(14)的修正辛格式稳定的充要条件为|ψ|≤1[27]。由式(17)易得

|≤2⟹

-5.308≤Δt2ξi≤0

(18)

由于得到稳定性解析表达式较困难，借由Liu等[17]的讨论可以得到

(19)

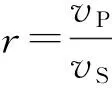
3.3 频散分析

数值频散是影响数值模拟结果的重要因素之一[28]。为了定量分析频散效应，定义数值频散比率

和采样率

式中λ为波长。则频散关系可进一步表示为[27]

(20)

式中ξS为由式(17)得到的特征值的最小绝对值，其对应于S波的特征值。

图2为数值频散误差曲线

(|R-1|cosφ, |R-1|sinφ)

在(x1,x2)平面上的投影，其中φ为波传播方向与x1轴的夹角，α=0.5。由图可见：在两种采样率的情况下，M1与M3的频散误差曲线交织在一起，几乎相同；在采用较小采样率时M1和M3的误差均小于M2(图2a)；当采用较大采样率时，在轴向上M2的误差略小于另外两种格式(图2b)。

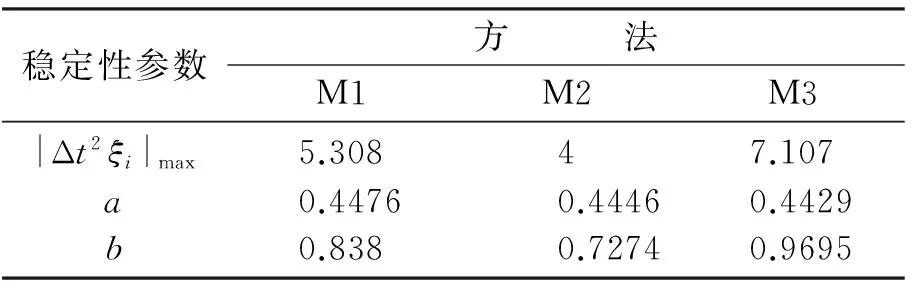
稳定性参数方 法M1M2M3|Δt2ξi|max5.30847.107a0.44760.44460.4429b0.8380.72740.9695

4 数值实验

4.1 拉梅问题

利用拉梅问题验证本文方法对弹性波数值模拟的计算精度和效率。图3为数值解与解析解[29]在水平与垂直方向的波形对比图。由图可见：由本文方法所得的数值解与解析解拟合较好(图3a、图3b)；局部放大图显示M1与M3相互叠加在一起，且与解析解拟合较好，而M2与解析解拟合略差，说明M1与M3的精度相当，且高于M2(图3c、图3d)。表2为三种方法的计算效率和精度对比。由表可见：M2用时最少(159.428s)，但是水平和垂直方向的误差总量较M1与M3偏大,与前文对二阶辛格式的分析认识一致；M1占用的计算内存最少，虽然其计算时间比M2多，但在计算时间少的情况下几乎与M3的计算精度相同。

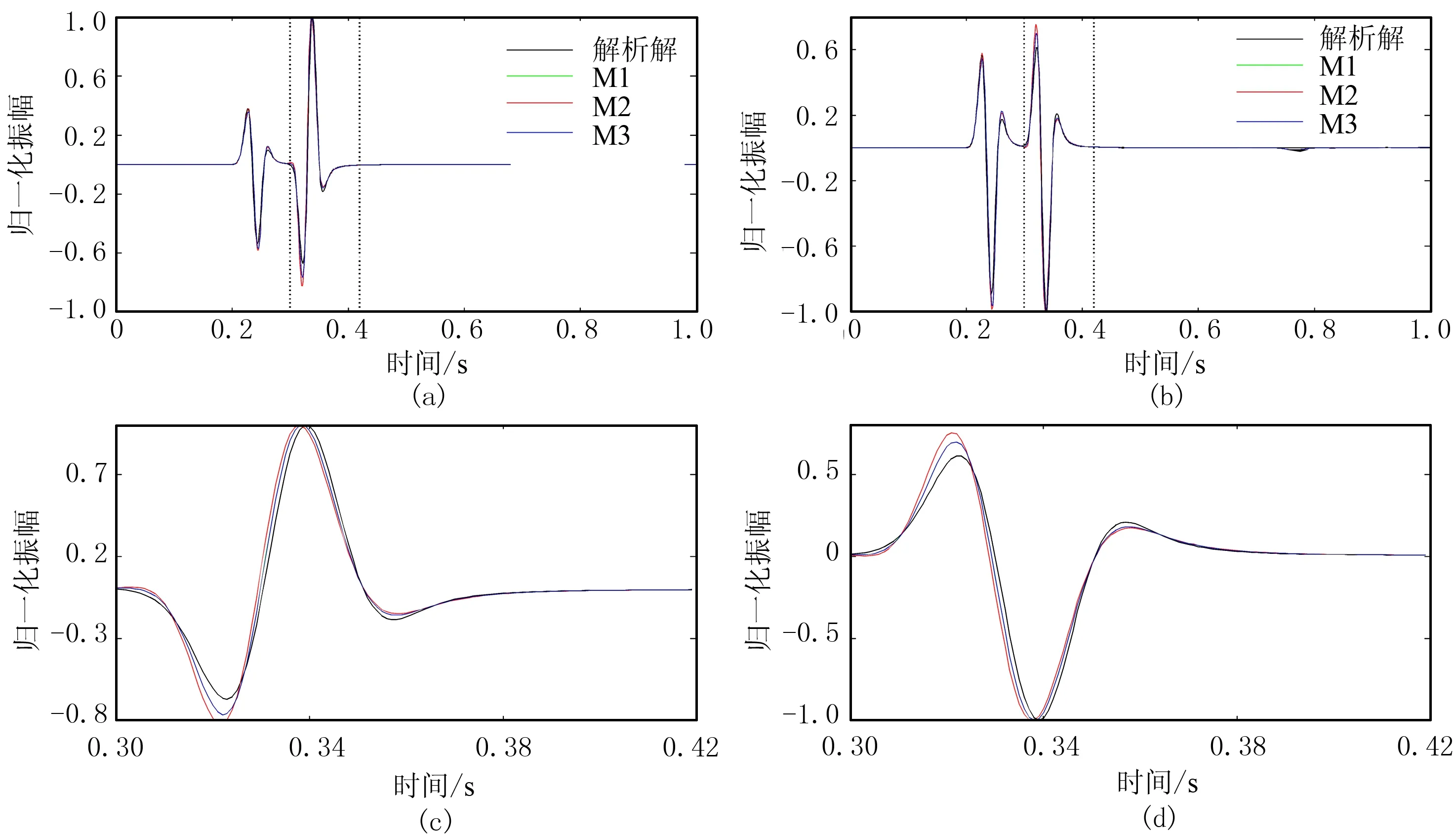
图3 数值解与解析解在水平与垂直方向的波形对比图 (a)水平分量； (b)垂直分量； (c)图a的局部放大； (d)图b的局部放大

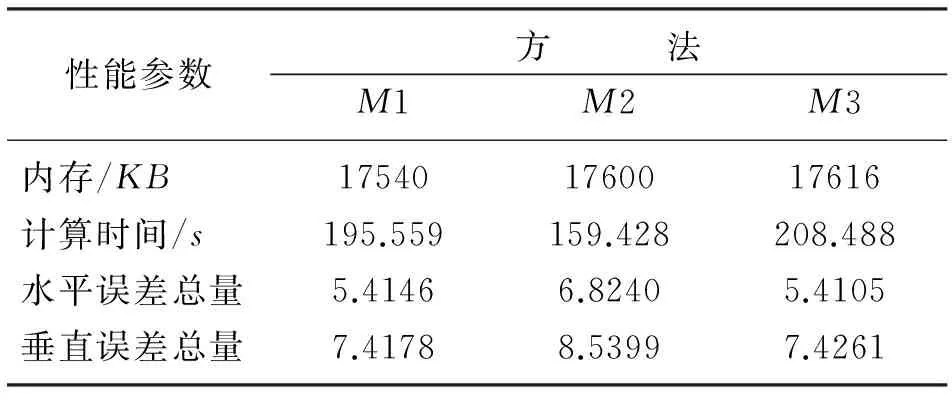
表2 三种方法的计算效率和精度对比

4.2 Sigsbee 2B速度模型

为了检验修正辛—准粒子法在非均匀介质模型中弹性波计算的稳定性，选取Sigsbee 2B速度模型(图4)进行测试。模拟结果如图5和图6所示。

图5为不同方法得到的Sigsbee 2B模型的水平位移分量波场快照。由图可见，当M1的时间步长大于M2、M3时，三种方法的波场模拟结果相似。

由于在非均匀介质模型中没有解析解，考虑到较小的时间步长可以取得更精确的结果，因此选择具有高阶时间精度的M3作为参考解，且令其一直取较小的时间步长不变。图6为检波点(3800m，1400m)处的水平位移分量记录对比图。由图可见，M1与M2取两种时间步长的结果与参考解相近，相互叠加在一起(图6a、图6b)，得到的M1、M2在时间步长为1、2ms时(与参考解)的误差曲线(图6c～图6f)表明，M1不论取较小的时间步长还是较大的时间步长，其误差均小于M2。数值结果证实了修正—准粒子方法在模拟弹性波方面的优越能力。

图4 Sigsbee 2B速度模型

模型速度变化范围为1437～4511m/s，选取模型的400×150个速度网格点，网格间距为20m。爆炸源为主频10Hz的Ricker子波,位于模型正中心，PML吸收层为20个网格厚度

图5 不同方法得到的Sigsbee 2B模型的水平位移分量波场快照 (a)M1(Δt=2ms,t=0.6s)； (b)M1(Δt=2ms,t=0.8s)； (c)M2(Δt=1ms,t=0.6s)； (d)M2(Δt=1ms,t=0.8s)； (e)M3(Δt=1ms,t=0.6s)； (f)M3(Δt=1ms,t=0.8s)

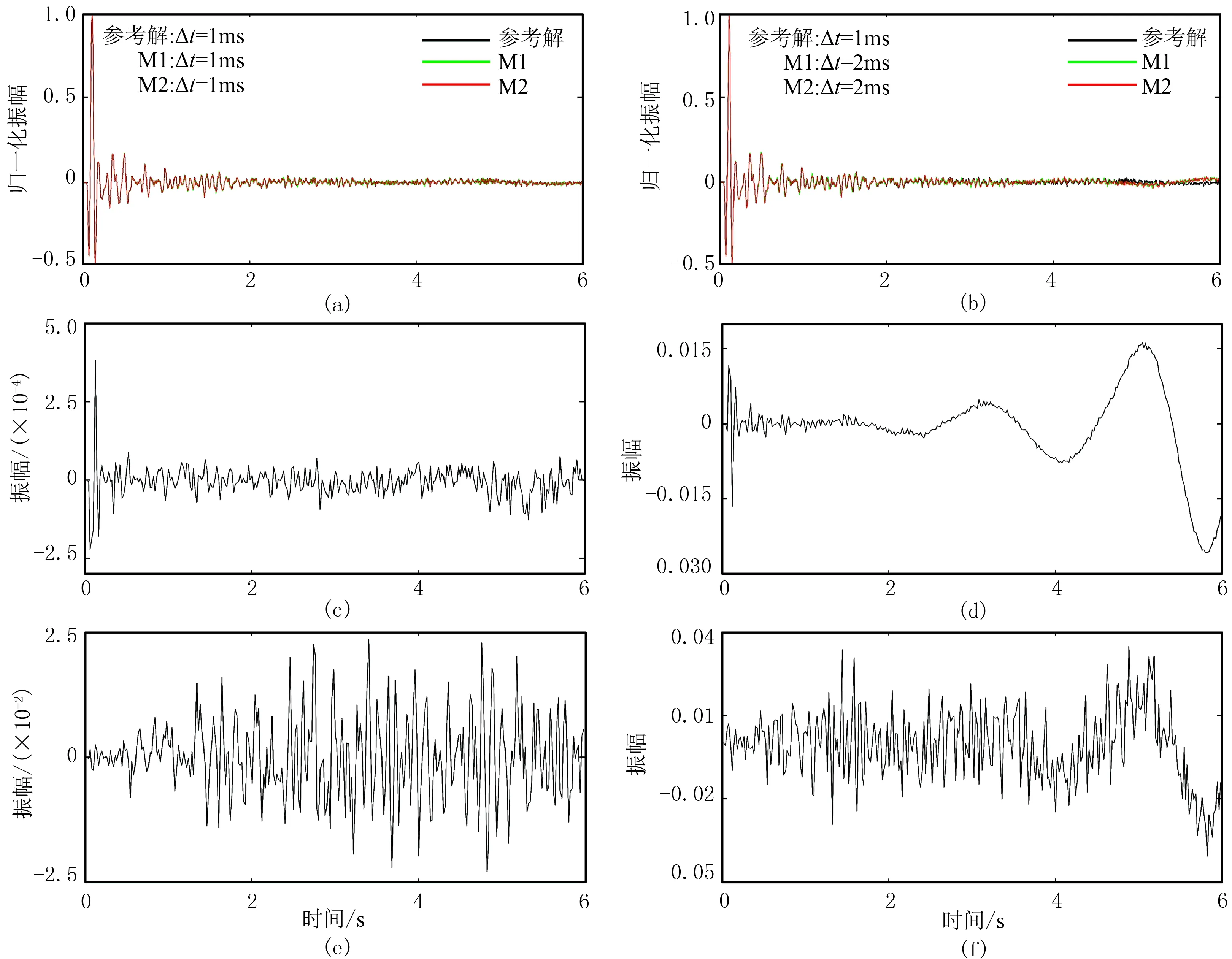
图6 检波点(3800m，1400m)处的水平位移分量记录对比图

(a)M1(Δt=1ms)、M2(Δt=1ms)、M3(Δt=1ms)的水平位移分量记录对比；(b)M1(Δt=2ms)、M2(Δt=2ms)、M3(Δt=1ms)的水平位移分量记录对比；(c)M1(Δt=1ms)误差曲线；(d)M1(Δt=2ms)误差曲线；(e)M2(Δt=1ms)误差曲线； (f)M2(Δt=2ms)误差曲线

在图a、图b中M3标注为参考解

5 结束语

时间离散方面，本文在二阶辛格式基础给出一种新的修正辛格式，并与空间准粒子离散方法相结合得到了地震波模拟的修正辛—准粒子法。结合理论推导与数值算例发现，修正辛—准粒子法在数值频散压制和数值稳定性提升等方面具有明显的优势。尚需指出，在空间离散方面，修正辛—准粒子法所采用的离散点较少，只考虑了粒子与其周围八个点的相互作用，需研究引入更多粒子参与计算的情况，并根据修正策略构造其他修正辛算法，并将算法与其他空间离散法相结合做进一步研究。

[1] 曹禹,杨孔庆.对声波和弹性波传播模拟的Hamilton系统方法.物理学报,2003,52(8):1984-1992. Cao Yu,Yang Kongqing.Hamiltonian system approach for simulation of acoustic and elastic wave propagation.Acta Physica Sinica,2003,52(8):1984-1992.

[2] Alford R,Kelly K,Boore D M.Accuracy of finite-diffe-rence.Geophysics,1974,39(6):834-842.

[3] Virieux J.P-SV wave propagation in heterogeneous media:velocity-stress finite-difference method.Geophysics,1986,51(4):889-901.

[4] Lysmer J,Drake L A.A finite element method for seismology.Methods in Computational Physics Advances in Research & Applications,1972,11:181-216.

[5] Moser F,Jacobs L J,Qu J.Modeling elastic wave propagation in waveguides with the finite element method.Ndt & E International,1999,32(4):225-234.

[6] Liu S,Li X,Wang W et al.A mixed-grid finite element method with PML absorbing boundary conditions for seismic wave modelling.Journal of Geophysics and Engineering,2014,11(5):055009.

[7] Fornberg B.High-order finite difference and the pseudospectral method on staggered grids.Siam Journal on Numerical Analysis,1990,27(4):904-918.

[8] 马德堂,朱光明.有限元法与伪谱法混合求解弹性波动方程.地球科学与环境学报,2004,26(1):61-64. Ma Detang,Zhu Guangming.Hybrid method combining finite difference and pseudospectral method for solving the elastic wave equation.Journal of Earth Sciences and Environment,2004,26(1):61-64.

[9] 唐怀谷,何兵寿.一阶声波方程时间四阶精度差分格式的伪谱法求解.石油地球物理勘探,2017,52(1):71-80. Tang Huaigu,He Bingshou.Pseudo spectrum method of first-order acoustic wave equation finite-difference schemes with fourth-order time difference accuracy.OGP,2017,52(1):71-80.

[10] Komatitsch D,Tromp J.The spectral-element me-thod,Beowulf computing,and global seismology.Science,2002,298(5599):1737-1742.

[11] 汪文帅.基于辛—谱元方法的地震波场模拟研究[学位论文].北京：中国科学院大学,2013.

[12] Yang D H,Teng J,Zhang Z et al.A nearly analytic discrete method for acoustic and elastic wave equations in anisotropic media.BSSA,2003,93(2):882-890.

[13] Chen Y,Song G,Xue Z et al.An improved optimal nearly analytical discretized method for 2D scalar wave equation in heterogeneous media based on the modified nearly analytical discrete operator.Geophy-sics,2014,79(6):T349-T362.

[14] 汪勇,段焱文,王婷等.优化近似解析离散化方法的二维弹性波波场分离模拟.石油地球物理勘探,2017,52(3):458-467. Wang Yong,Duan Yanwen,Wang Ting et al.Numerical simulation of elactic wave separation in 2D isotropic medium with the optimal nearly-analytic discretization.OGP,2017,52(3):458-467.

[15] Takekawa J,Madariage R,Mikada H et al.Numerical simulation of seismic wave propagation produced by earthquake by using a particle method.Geophysical Journal International,2012,191(3):1305-1316.

[16] Suzuki Y,Koshizuka S,Oka Y.Hamiltonian moving-particle semi-implicit (HMPS) method for incompressible fluid flows.Computer Methods in Applied Mechanics and Engineering,2007,196(29-30):2876-2894.

[17] Liu S,Yang D,Ma J.A modified symplectic PRK scheme for seismic wave modeling.Computers & Geosciences,2017,99:28-36.

[18] 罗明秋,刘洪,李幼铭.地震波传播的哈密顿表述及辛几何算法.地球物理学报,2001,44(1):120-128. Luo Mingqiu,Liu Hong,Li Youming.Hamiltonian description and symplectic method of seismic wave propagation.Chinese Journal of Geophysics,2001,44(1):120-128.

[19] Chen J B.High-order time discretizations in seismic modeling.Geophysics,2007,72(5):SM115-SM122.

[20] Liu S,Li X,Wang W et al.A new kind of optimal se-cond-order symplectic scheme for seismic wave simulations.Science in China:Earth Sciences,2014,57(4):751-758.

[21] Liu S,Yang D,Lang C et al.Modified symplectic schemes with nearly-analytic discrete operators for acoustic wave simulations.Computer Physics Communications,2017,213:52-63.

[22] Liu S,Li X,Wang W et al.A modified symplectic scheme for seismic wave modeling.Journal of Applied Geophysics,2015,116(5):110-120.

[23] 冯康.哈密尔顿系统的辛几何算法.浙江杭州：浙江科技出版社,2003.

[24] 马毅恒,井西利,邢小宁等.弹性波的三维Hamilton系统方法模拟.石油地球物理勘探,2012,47(4):524-531. Ma Yiheng,Jing Xili,Xing Xiaoning et al.3D Hamiltonian system approach simulation for elastic wave.OGP,2012,47(4):524-531.

[25] 刘少林,李小凡,汪文帅等.求解弹性波方程的辛RKN格式.地球物理学报,2015,58(4):1355-1366. Liu Shaolin,Li Xiaofan,Wang Wenshuai.A symplectic RKN scheme for solving elastic wave equations.Chinese Journal of Geophysics,2015,58(4):1355-1366.

[26] Li X,Li Y,Zhang M et al.Scalar seismic-wave equation modeling by a multisymplectic discrete singular convolution differentiator method.BSSA,2011,101(4):1710-1718.

[27] Basabe J D D,Sen M K.Grid dispersion and stability criteria of some common finite-element methods for acoustic and elastic wave equations.Geophysics,2007,72(6):T81-T95.

[28] 梁文全,王彦飞,杨长春.声波方程数值模拟矩形网格有限差分系数确定法.石油地球物理勘探,2017,52(1):56-62. Liang Wenquan,Wang Yanfei,Yang Changchun.Acoustic wave equation modeling with rectangle grid finite difference operator and its linear time space domain solution.OGP,2017,52(1):56-62.

[29] De Hoop A.A modification of Cagniard's method for solving seismic pulse problems.Applied Scientific Research,Section B,1960,8(1):349-356.