一维频率域中观尺度虚岩石物理方法

吴建鲁 吴国忱

(①中国石油大学(华东)地球科学与技术学院，山东青岛 266580;②海洋国家实验室海洋矿产资源评价与探测技术功能实验室，山东青岛 266071)

1 引言

地震波在地下双相介质中传播时会发生速度频散和能量衰减。20世纪50年代以来，许多学者对地震波在双相介质中的衰减机理做了大量研究。从研究地震波衰减因素尺度的角度出发，可将地震波衰减机制分为三类，即宏观尺度、微观尺度和中观尺度[1，2]。由宏观尺度“Biot流”[3-5]和微观尺度“挤喷流”[6]引起的地震波衰减都无法预测地震频带的衰减和频散。White等[7，8]在考虑中观尺度(远大于孔隙尺寸且小于地震波长的尺度定义为中观尺度)流体斑块饱和情况时，预测了地震波在地震频带的衰减和频散。随后人们针对中观尺度的衰减和频散机理做了大量的理论研究[9-16]，结果表明地下介质的中观尺度非均质性对地震波在地震频带的衰减起主控作用。

在构建特定理想化岩石物理模型的基础上发展特定的地震波衰减理论是研究地震波衰减和频散特征的重要手段和方法。但是由于实际介质的岩性、流体斑块结构、岩石孔渗性差异等因素的复杂变化，理论模型往往无法与实验测量的结果进行精确的匹配分析，从而无法验证理论的正确性和适用条件等[17-19]。Masson等[20，21]将低频形式的动态渗透率关系式转换至时间域后，采用准静态时间域有限差分交错网格方法，利用Biot弹性波方程首次针对中观尺度非均质模型进行虚岩石物理理论分析，并将该方法推广至全频带。针对中观尺度非均质性，Quintal等[22]和Rubino等[23]采用有限元法进行地震波衰减和速度频散的研究。由于地下油气储层与地震频带的衰减和频散有着密切的联系，所以针对由中观尺度非均质性引起的地震波衰减和频散研究、了解地震波在双相介质中的传播规律十分必要[24-26]。基于地震波衰减理论，前人也利用实际地震资料进行了地震波衰减信息提取及储层预测方面的研究[27-30]。

本文借鉴准静态模拟思路，用频率域有限差分法开展中观尺度非均质虚岩石物理模型的研究。与时间域虚岩石物理方法相比，该方法既可以直接求取任一频率下的地震波衰减和频散速度，便于应用于实际岩样的地震波衰减预测分析，又消除了针对频率域的动态渗透率公式进行近似带来的误差，也避免了讨论在岩样外表面施加的力源函数表达式及时间剖分稳定性等问题。首先通过数值计算模拟不同数量特征单元叠置模型的地震波衰减和频散，说明了特征单元表征模型衰减信息的唯一性；随后分析了相同含气饱和度条件下不同非均匀尺度及斑块结构模型的地震波衰减和频散；最后，计算了三相流体周期性层状介质的地震波衰减和频散结果及模型的位移与应力的频率域空间分布特征，可知不同流体之间的中观尺度相对流动是诱导地震波在地震频带衰减的主控因素。

2 一维形式双相介质理论

本文主要采用前人推导的两种双相介质的控制方程：第一种为无耗散力的线性固结耦合的准静态方程[31]；第二种为考虑流体黏滞性导致能量耗散双相介质方程[3-5]。前者未考虑体力耗散，可以精确地描述地震频带内波的传播特征，后者考虑了由宏观尺度流固相对运动摩擦导致的“Biot”流，进而产生地震波高频衰减，前者是后者的低频形式。通过对这两种控制方程的研究，可以全面检验本文所提出的一维频率域虚岩石物理方法的准确性。

在假设孔隙介质的应力散度为零的前提下，线性固结耦合的准静态Biot方程在频率—空间域的一维形式[32]为

(1)

Biot在考虑宏观尺度“Biot流”的基础上推导了饱和流体孔隙介质条件下的本构方程，初步建立了地震波在双相介质中传播的理论框架，成为后人研究地震波在双相介质中传播的理论基础[2，3]。其含流体孔隙介质弹性波传播的一维控制方程为

(2a)

(2b)

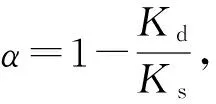
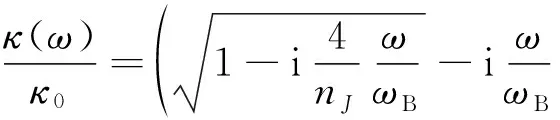
(3)

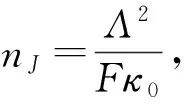
3 一维频率域准静态虚岩石物理方法

当外界施加一定的力时，岩石样本会产生形变(图1)，通过对上述两种孔隙介质地震波控制方程微分项进行常规空间离散

(4)

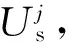
(5)

式中L为模型的长度。利用压力P0与体应变θ的比值可求取模型的复变模量E，即

(6)

从而获取模型的地震波衰减因子Q-1(ω)和频散速度VP(ω)

(7)

在上、下施加垂直方向外力P0时，为保证岩石物理模型的封闭条件，使上、下边界的流体位移Uf为零，则模型的上、下边界条件为

(8)

与传统的频率域有限差分数值模拟方法相比，上述的频率域虚岩石物理方法不需要吸收边界条件，减小了模型网格的剖分数量，提高了数值计算效率。

图1 一维虚岩石物理模型示意图

4 数值计算结果

为验证频率域一维虚岩石物理方法的有效性，利用周期性层状斑块饱和模型(图2a，介质参数见表1)进行数值模拟，其非均质尺度为中观尺度。饱含两种不同液相水平层状孔隙介质周期性交互排列，横向无限延伸，仅考虑垂直方向一维应力—应变响应。首先考虑含气砂岩与含水砂岩周期排列情况，各层厚度均为0.1m，即含气饱和度为0.5，空间网格步长dz设为1mm，采用该模型特征单元(图2b)进行地震波衰减和频散模拟，结果如图3所示，其中曲线“Biot1941”和曲线“Biot1956”分别为基于准静态控制方程(式(1))和考虑宏观尺度“Biot流”的双相介质控制方程(式(2))求取的结果，曲线“White1975”为利用White等[8]基于周期性层状介质的复变模量解析解的结果(解析解公式参见文献[8，14])。由图可见，地震波衰减和频散对频率有很强的依赖性，这与前人的实验室测量结果[17]一致。与解析解相比，基于两种双相介质传播方程、采用本文所描述的频率域有限差分方法可以获取精确的地震波衰减和频散结果，曲线“Biot1956”在高频带地震波速度迅速降低，因为在此频带内地震波波长与模型尺度相当，地震波产生共振现象，为地震波能量传播停滞所致[6，10]。

表1 孔隙介质参数

图4为针对周期性层状介质斑块饱和模型，基于准静态控制方程和考虑宏观尺度“Biot流”的双相介质控制方程模拟不同频率下特征单元(图2b)的应力、固体位移、流体位移及流体压力的分布。由图可见，基于准静态假设的双相介质控制方程正演模拟的应力场为常数，与其方程描述的应力场散度为零的条件一致，而基于考虑宏观尺度“Biot流”的双相介质控制得到的应力场在高频振荡变化，这直观展示了地震波发生共振时的应力场分布特征(图4a)。当某一特定频带内固体位移、流体位移及流体压力空间变化较大(即梯度较大)时，则产生的地震波衰减和频散相对较强。本文仅讨论地震频带附近的地震波衰减和频散，即不考虑高频带宏观尺度“Biot流”引起的地震波共振影响，故下文采用准静态Biot的双相介质控制方程。

分别对图2b～图2d描述的特征单元采用频率域模拟方法求取地震波衰减和频散，分析特征单元数量对周期性层状介质斑块饱和模型的地震波衰减和频散的影响(图5)。由图可见，周期性层状介质的斑块饱和模型的地震波衰减和频散不受特征单

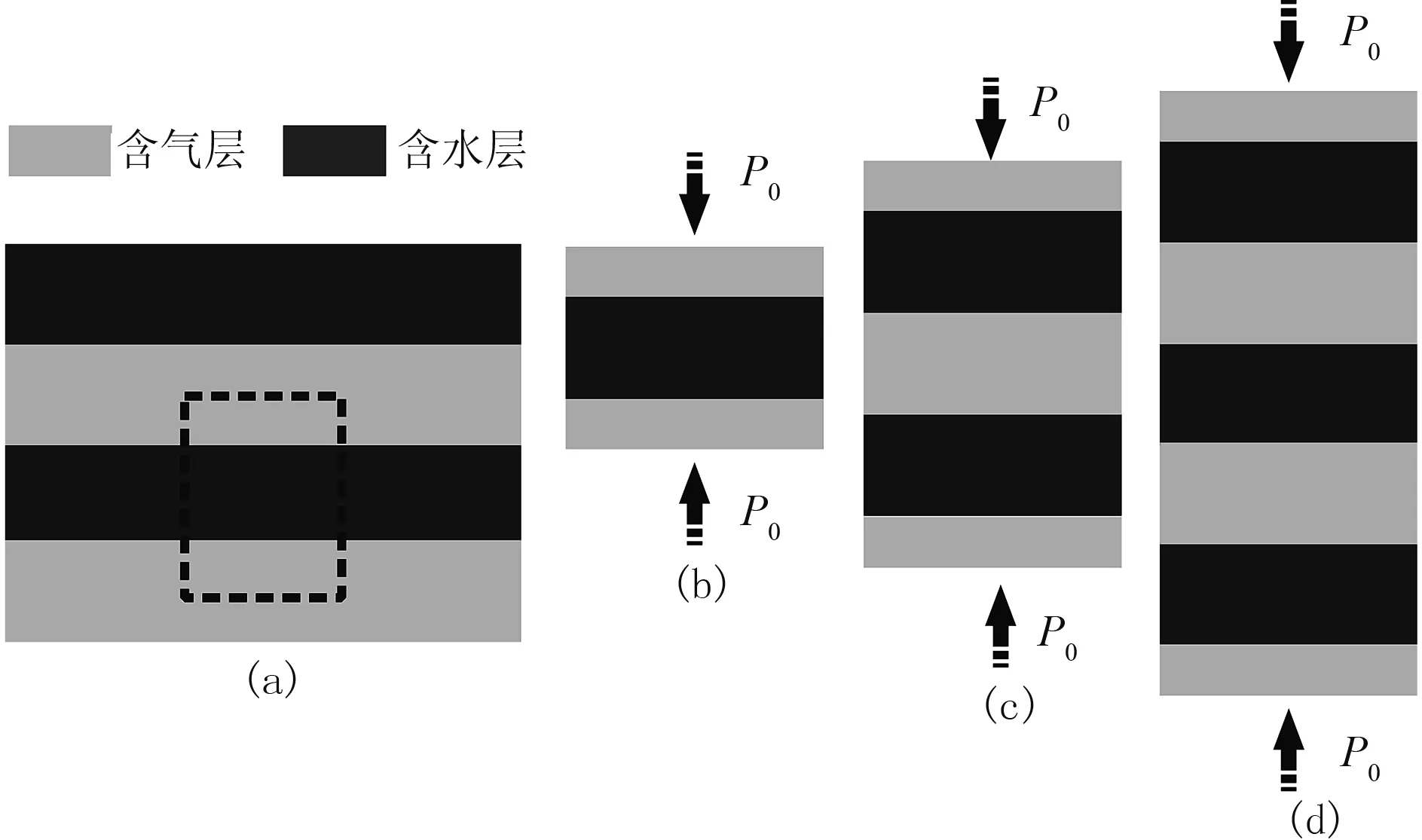
图2 周期性层状斑块饱和模型及其特征单元示意图 (a)周期性层状模型示意图； (b)单个特征单元； (c)两层特征单元叠置； (d)三层特征单元叠置

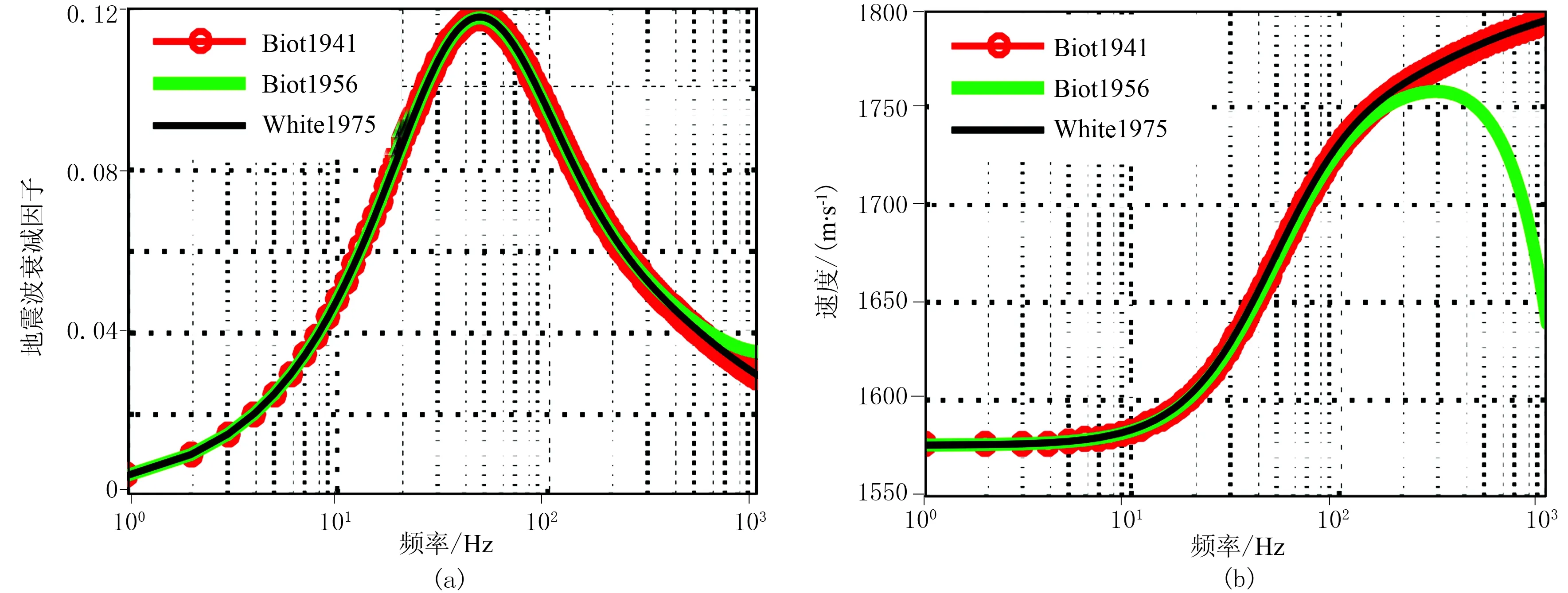
图3 周期性层状斑块饱和介质模型的地震波衰减(a)和频散(b)模拟结果

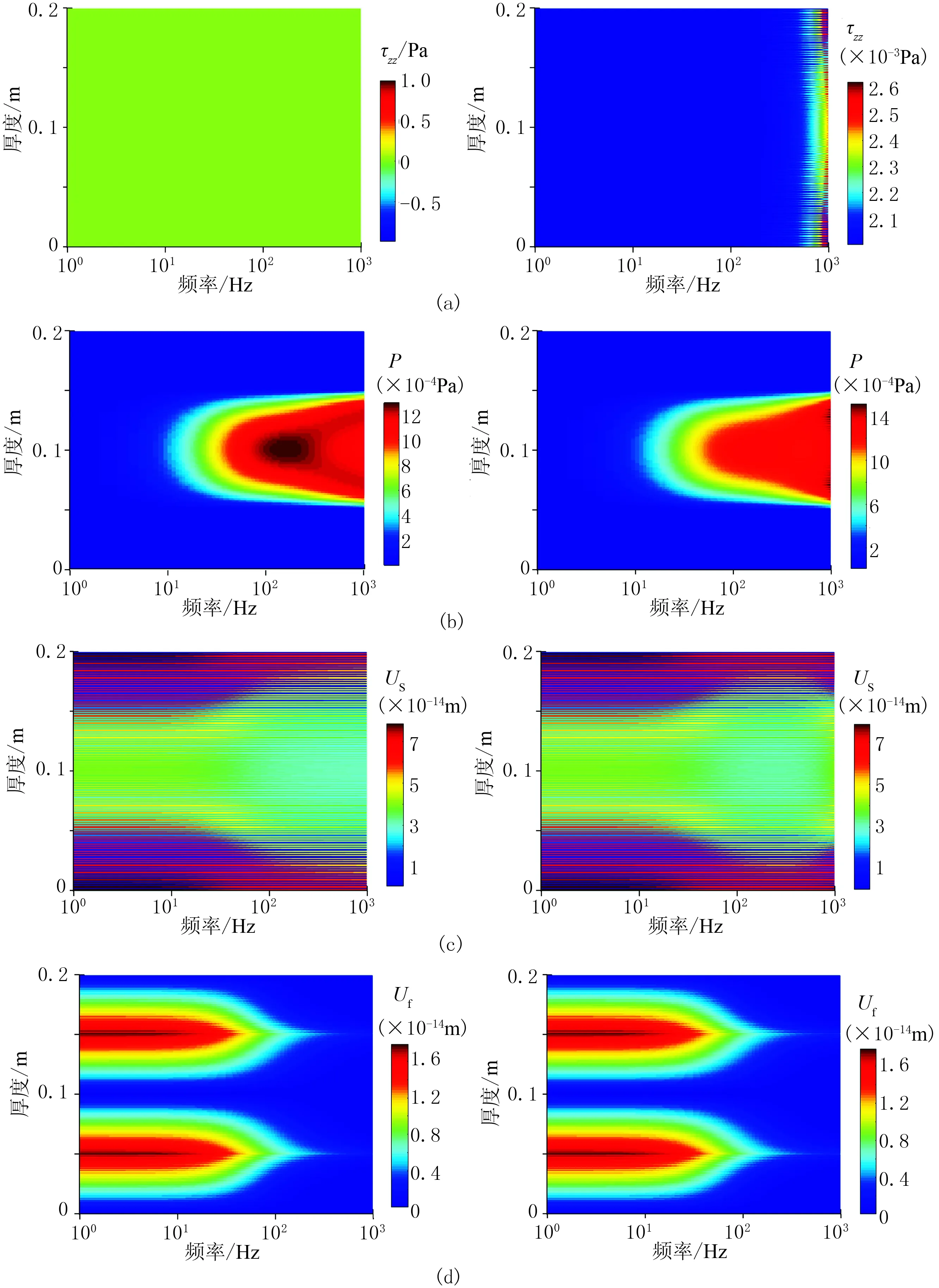
图4 基于准静态控制方程(左)和考虑宏观尺度“Biot流”的双相介质控制方程(右)数值模拟结果 (a)应力； (b)流体压力； (c)固体位移； (d)流体位移

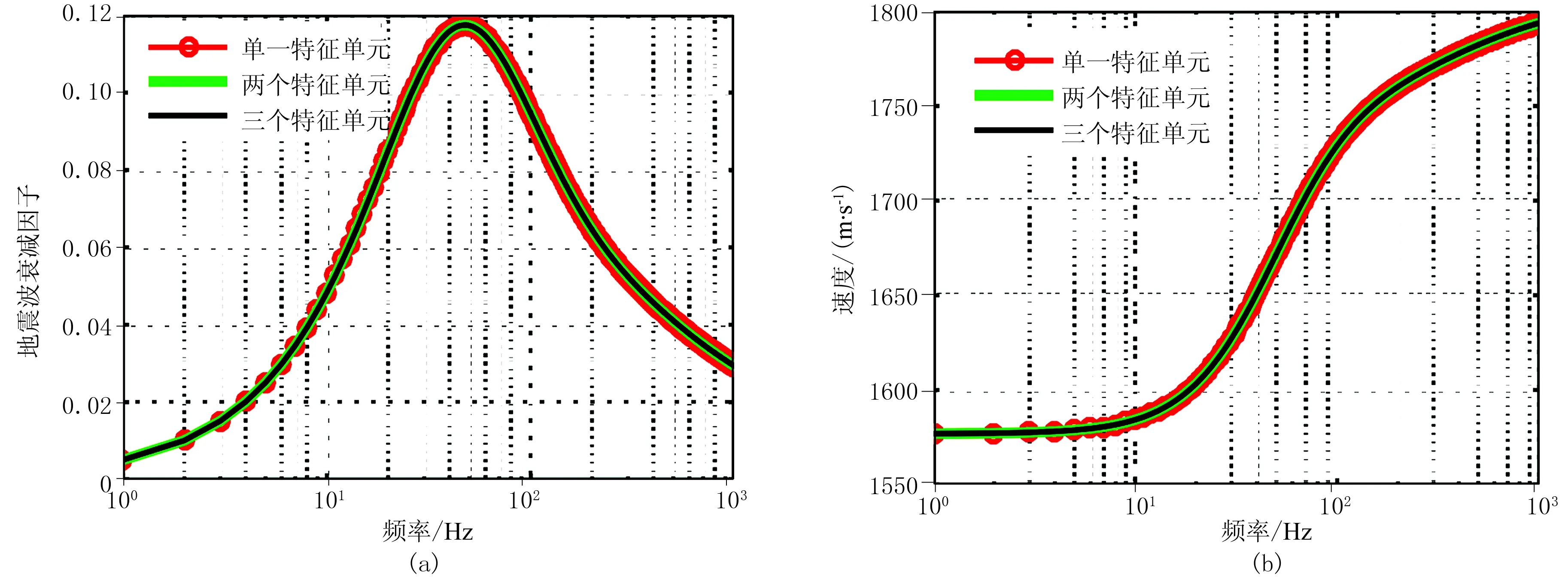
图5 不同个数特征单元叠加的地震波衰减(a)和频散(b)模拟结果

元数量的影响，验证了本文数值求取方法的稳定性，表明该模型表征的地震波衰减和频散的唯一性。

图6为相同含气饱和度下不同斑块分布的特征单元示意图，含气或含水的特征单元的总厚度设为0.12m，空间网格步长为1mm。特征单元一与周期性层状介质斑块饱和模型的特征单元相同； 特征单元二上、下分别为厚度0.12m的含气、含水孔隙介质； 特征单元三、四则把含气层与含水层分别进行二、四等分后交互排列，单个液相的介质非均匀尺寸逐渐减小； 特征单元五、六、七、八中的含气和水孔隙介质分别按1∶2比例进行等分，然后进行如图所示的排列组合。由于所构建的上述特征单元不再是周期性层状介质模型所模拟的理想介质，其解析解求取十分困难，所以采用本文提出的数值模拟算法求解各个特征单元的地震波衰减和频散，结果如图7所示。由特征单元一到特征单元四的地震波衰减和频散结果可知： 当非饱和流体的非均匀尺度逐渐减小时，地震波衰减主频向高频段移动，频带变宽；当非饱和流体的非均匀尺度不变，流体斑块尺度组合关系不同时，则求取的数值模拟结果会存在差异，如图7中特征单元五～八的计算结果所示； 当含气饱和度及非均匀尺度不变时，其中下部含水孔隙介质的层厚对地震波的衰减和频散结果起主导作用，且由于存在多种形式非均质组合，特征单元五、六的地震波衰减出现“多峰”现象。从不同特征单元的速度频散结果(图7b)可见，在相同含气饱和度条件下，不同非均匀尺度情况地震波频散速度曲线也存在差异。值得注意的是，不同特征单元频散速度的高、低频极限还是一致的。

图6 相同含气饱和度下不同斑块饱和分布示意图 浅色表示含气层；深色表示含水层

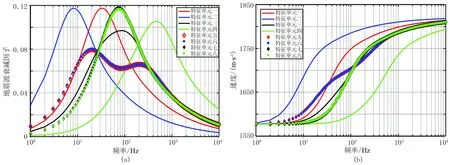
图7 不同特征单元的地震波衰减(a)和频散(b)模拟曲线

为进一步讨论多相孔隙介质中观尺度非均匀饱和情况的地震波衰减和频散，采用频率域模拟方法模拟含三相流体周期性层状介质模型(图8)的地震波衰减和频散及高、低频极限(图9)，并分析应力场、固体位移、流体位移及流体压力的变化情况[6](图10)。模拟时油的参数设置为：Koil=1GPa；ρoil=700kg/m3；ηoil=0.04Pa·s。当地震波在该模型中传播时，多相流体之间会存在不同情况中观尺度“局域流”现象(图10)，从而发生不同频带的地震

波衰减和频散，即存在地震波衰减“双峰”现象。高、低频带的地震波衰减分别是由气相与油相、水相之间的相对流体产生的，由于油、水之间的物性(模量、黏滞性及密度等)差别不大，引起的地震波衰减较小，无法体现在计算结果之中，说明当非饱和地下储层赋存一定的天然气时，储层的地震波衰减特征比较明显，有利于油气储层等方面的研究。

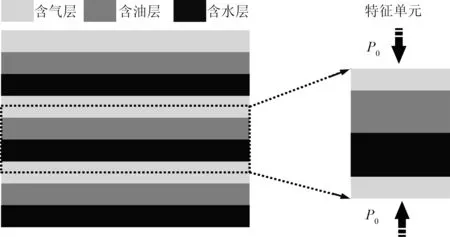
图8 三相流体周期性层状介质示意图

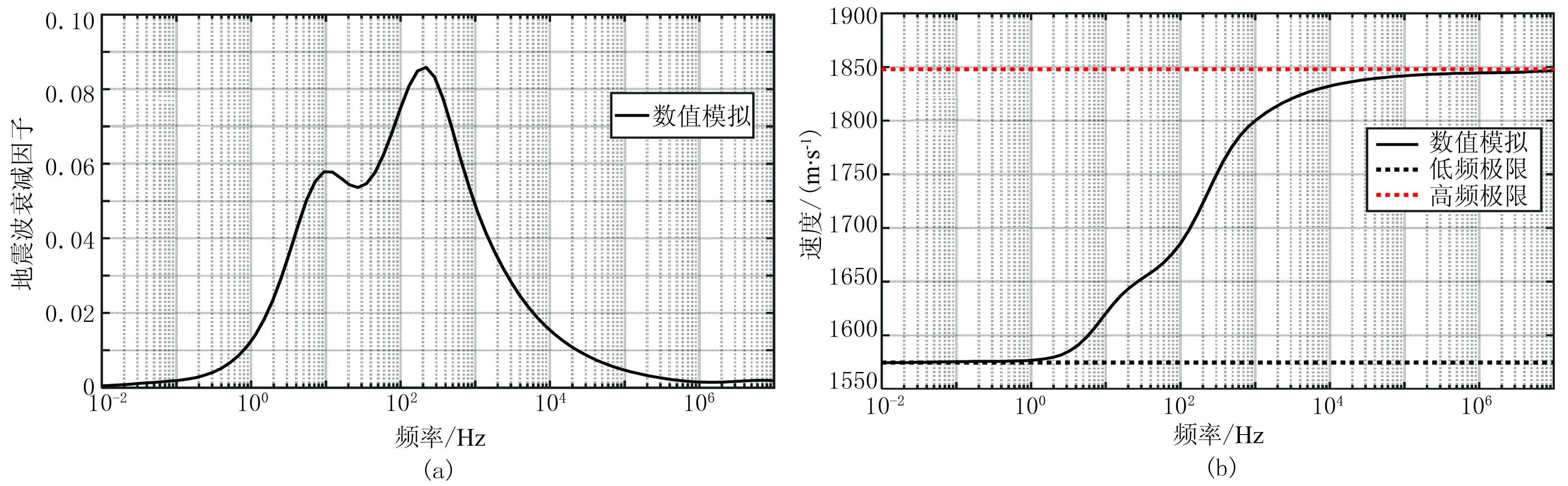
图9 三相流体周期性层状介质的地震波衰减(a)和频散(b)模拟曲线

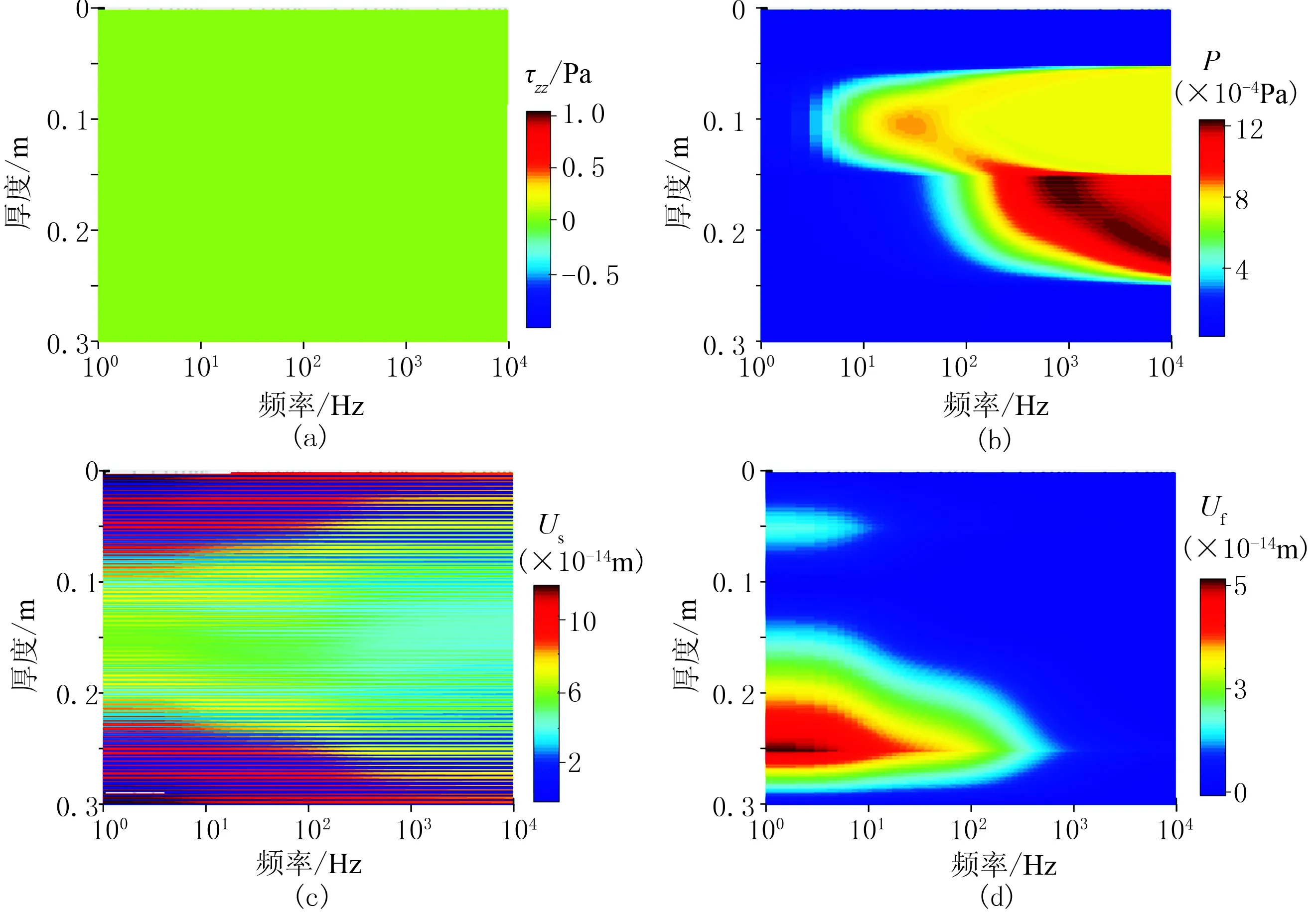
图10 三相流体周期性层状介质模型应力场(a)、流体压力(b)、固体位移(c)及流体相对位移(d)模拟结果

5 认识与讨论

地震波在地下含流体孔隙介质中传播时，中观尺度的“局域流”衰减机制是引起地震波在地震频带产生衰减和频散的主要因素。在前人针对中观尺度“局域流”的研究的基础上，利用Biot(1941)准静态方程和考虑宏观尺度“Biot流”的Biot(1956)双相介质方程，采用频率域有限差分模拟方法，应用周期性层状斑块饱和模型验证了本文方法的有效性。本文方法不受模型特征单元数量影响，可以模拟任意形式斑块分布的一维双相介质模型，突破了理论解析特征单元理想的假设条件。利用该方法进一步分析了相同含气饱和度条件下不同结构斑块饱和尺度模型和三相流斑块模型的地震波衰减和频散。斑块饱和非均质结构不同，产生的地震波衰减和频散也不相同，当非饱和流体储层中含有一定的天然气时，地震波衰减相对较大，表明了利用地震波衰减进行油气预测的潜在价值。另一方面，该方法可以获取岩石物理模型任意频率的地震波衰减和频散信息，便于与岩石物理实验中测量结果进行对比分析。

本文针对一维模型的频率域地震波衰减和频散模拟方法精度较高，但模型为二维甚至三维时，由于地震波传播方程的参数变量多，建立的阻抗矩阵大，存在一定的不适用性。这就需要减少波动方程的参数变量的个数，增加边界条件的微分阶数，以提高算法的适用性。

[1] Dvorkin J，Nur A.Dynamic poroelasticity：a unified model with the squirt and the Biot mechanisms.Geophysics，1993，58(4)：524-533.

[2] 张广智，何锋，张佳佳等.微观与介观波致流下的速度频散与衰减.石油地球物理勘探， 2017，52(4)：743-751. Zhang Guangzhi，He Feng，Zhang Jiajia et al.Velocity dispersion and attenuation at microscopic and mesoscopic wave-induced fluid flow.OGP，2017，52(4)：743-751.

[3] Biot M A.Theory of propagation of elastic waves in a fluid-saturated porous solid Ⅰ：Low-frequency range.The Journal of the Acoustical Society of America，1956，28(2)：168-178.

[4] Biot M A.Theory of propagation of elastic waves in a fluid-saturated porous solid Ⅱ：Higher-frequency range.The Journal of the Acoustical Society of America，1956，28(2)：179-191.

[5] Biot M A.Mechanics of deformation and acoustic propagation in porous media.Journal of Applied Physics，1962，33(4)：1482-1498.

[6] Müller T，Gurevich B，Lebedev M.Seismic wave attenuation and dispersion resulting from wave-induced flow in porous rocks — A review.Geophysics，2010，75(5)：A147-A164.

[7] White J E.Computed seismic speeds and attenuation in rocks with partial gas saturation.Geophysics，1975，40(2)：224-232.

[8] White J E，Mikhayloya N G，Lyakhovitskiy F M.Low-frequency seismic waves in fluid-saturated layered rocks.Physics of the Solid Earth，1975，11(10)：654-659.

[9] 席道瑛，邱文亮，程经毅等.饱和多孔岩石的衰减与孔隙率和饱和度的关系.石油地球物理勘探， 1997， 32(2)：196-201. Xi Daoying，Qiu Wenliang，Cheng Jingyi et al.Relation between attenuation and porosity or saturation of rock.OGP，1997，32(2)：196-201.

[10] 刘炯，马坚伟，杨慧珠.White球状Patchy模型中纵波传播研究.地球物理学报，2010，53(4)：954-962. Liu Jiong，Ma Jianwei，Yang Huizhu.Research on P-wave’s propagation in White’s sphere model with patchy saturation.Chinese Journal of Geophysics，2010，53(4)：954-962.

[11] 邓继新，王尚旭，杜伟.介观尺度孔隙流体流动作用对纵波传播特征的影响研究——以周期性层状孔隙介质为例.地球物理学报，2012，55(8)：2716-2727. Deng Jixin，Wang Shangxu，Du Wei.A study of the influence of mesoscopic pore fluid flow on the propagation properties of compressional wave — a case of periodic layered porous media.Chinese Journal of Geo-physics，2012，55(8)：2716-2727.

[12] 吴国忱，吴建鲁，宗兆云.周期性层状含孔隙、裂隙介质模型纵波衰减特征.地球物理学报，2014，54(8)：2666-2677. Wu Guochen，Wu Jianlu，Zong Zhaoyun.The attenuation of P wave in a periodic layered porous media containing cracks.Chinese Journal of Geophysics，2014，54(8)：2666-2677.

[13] Nicola T，Quintal B.Seismic attenuation in partially saturated rocks：Recent advances and future directions.The Leading Edge，2014，33(2)：640-646.

[14] 吴建鲁，吴国忱，宗兆云.含混合裂隙、孔隙介质的纵波衰减规律研究.地球物理学报，2015，57(4)：1378-1389. Wu Jianlu，Wu Guochen，Zong Zhaoyun.Attenuation of P waves in a porous medium containing various cracks.Chinese Journal of Geophysics，2015，57(4)：1378-1389.

[15] 李世凯，文晓涛，阮韵淇等.基于黏滞—弥散理论的含气砂岩数值模拟与分析.石油地球物理勘探， 2017，52(4)：752-759. Li Shikai，Wen Xiaotao，Ruan Yunqi et al.Sandstone gas reservoir simulation and analysis based on diffusive-viscous theory.OGP，2017，52(4)：752-759.

[16] 陈程，文晓涛，郝亚炬等.基于White模型的砂岩储层渗透率特性分析.石油地球物理勘探，2015，50(4)：723-729. Chen Cheng，Wen Xiaotao，Hao Yaju et al.Sandstone reservoir permeability characteristics analysis based on White model.OGP，2015，50(4)：723-729.

[17] Batzle M，Han D，Hofmann R.Fluid mobility and frequency-dependent seismic velocity — Direct measurements.Geophysics，2006，71(1)：N1-N9.

[18] Madonna C，Tisato N.A new seismic wave attenua-tion module to experimentally measure low-frequency attenuation in extensional mode.Geophysical Prospecting，2013，61(2)：302-314.

[19] McCann C，Sothcott J，Best A I.A new laboratory technique for determining the compressional wave properties of marine sediments at sonic frequencies and in situ pressures.Geophysical Prospecting，2014，62(1)：97-116.

[20] Masson Y J，Pride S R，Nihei K T.Finite difference modeling of Biot’s poroelastic equations at seismic frequencies.Journal of Geophysical Research：Solid Earth，2006，111(10)：B10305.

[21] Masson Y J，Pride S R.Poroelastic finite difference modeling of seismic attenuation and dispersion due to mesoscopic-scale heterogeneity.Journal of Geophysical Research：Solid Earth，2007，112(3)：B03204.

[22] Quintal B，Steeb H，Frehner M et al.Quasi-static finite element modeling of seismic attenuation and dispersion due to wave-induced fluid flow in poroelastic media.Journal of Geophysical Research：Solid Earth，2011，116(B1)：B01201.

[23] Rubino J G，Holliger K.Seismic attenuation and velocity dispersion in heterogeneous partially saturated porous rocks.Geophysical Journal International，2012，188(3)：1088-1102.

[24] 黄中玉，王于静，苏永昌.一种新的地震波衰减分析方法——预测油气异常的有效工具.石油地球物理勘探，2000，35(6)：768-773. Huang Zhongyu，Wang Yujing，Su Yongchang.A new analysis method for seismic wave attenuation effective tool for predicting hydrocarbon anomaly.OGP，2000，35(6)：768-773.

[25] 张会星，何兵寿，姜效典等.利用地震波在双相介质中的衰减特性检测油气.石油地球物理勘探，2010，45(3)：343-349. Zhang Huixing，He Bingshou，Jiang Xiaodian et al.Utilizing attenuation characteristic of seismic wave in dual-phase medium to detect oil and gas.OGP，2010，

45(3)：343-349.

[26] 张大伟，孙赞东，王学军等.利用零井源距VSP资料进行品质因子反演.石油地球物理勘探，2011，46(S1)：47-52. Zhang Dawei，Sun Zandong，Wang Xuejun et al.Q-factor inversion and calculation using zero-offset VSP data.OGP，2011，46(S1)：47-52.

[27] 兰锋，李明，李艳东等.应用黏弹性波动方程模拟地震低频阴影.石油地球物理勘探，2015，50(1)：84-90. Lan Feng，Li Ming，Li Yandong et al.Low-frequency shadow numerical simulation with visco-elastic wave equation.OGP，2015，50(1)：84-90.

[28] Wu X，Chapman M，Li X et al.Quantitative gas saturation estimation by frequency-dependent amplitude-versus-offset analysis.Geophysical Prospecting，2014，62(6)：1224-1237.

[29] Innanen K A，Mahmoudian F.Characterizing the de-gree of amplitude-variation-with-offset nonlinearity in seismic physical modelling reflection data.Geophysical Prospecting，2014，62(6)：1-8.

[30] 胡军辉，文晓涛，许艳秋等.利用黏滞—弥散波动方程理论进行油水识别.石油地球物理勘探，2016，51(3)：556-564. Hu Junhui，Wen Xiaotao，Xu Yanqiu et al.Oil-water recognition based on diffusive-viscous wave equation.OGP，2016，51(3)：556-564.

[31] Cavallini F，Carcione J M，Vidal De Ventós D et al.Low-frequency dispersion and attenuation in anisotropic partially saturated rocks.Geophysical Journal International，2017，209(3)：1572-1584.

[32] Biot M A.General theory of three-dimensional consoli-dation.Journal of Applied Physics，1941，12(2)：155-164.