求解LTI 系统零状态响应过程中的解法辨析
2019-08-23 10:41马丁
数字通信世界 2019年7期
马 丁
(南昌航空大学科技学院,南昌 330034)
由线性时不变(LTI)系统的特性可知,其零状态响应yf(t)等于输入信号f(t)与系统的单位冲激响应h(t)的卷积。即如果已知单位冲激信号δ(t)作用在系统上的响应h(t),利用卷积即可求得任意连续信号f(t)作用在系统上的零状态响应。可见系统冲激响应的求解和卷积的计算是求解系统零状态响应的关键。本文以h(t)的求解为重点,将两种主流方法加以对比,并指出容易陷入的误区。
例:求下列系统的零状态响应

1 单位冲激响应h(t)
1.1 冲激平衡法


1.2 傅里叶反变换法


(2)H(jω)的表达式中后两项均为单边指数信号的傅立叶变换,故推测第一项求反变换之后不应出现符号函数这种特殊项。

另外用单边拉普拉斯变换也极易求出上述结果。
2 零状态响应yf(t)
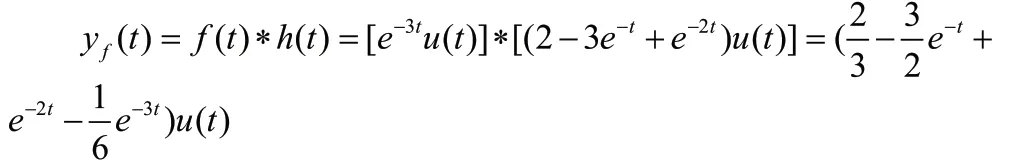
3 结束语
求单位冲激响应h(t)时,用冲激平衡法及傅里叶反变换法均可得到正确的结果,前者过程繁琐,后者较为简便。但如果忽略了已知条件t>0的限制,单纯地利用(-∞,+∞)上常见函数的傅里叶变换对来求反变换,往往会得到错误的结论,这一点需要格外注意。
猜你喜欢
心声歌刊(2022年3期)2022-06-06
心声歌刊(2022年3期)2022-06-06
北京航空航天大学学报(2021年9期)2021-11-02
少儿科技(2021年12期)2021-01-20
电子制作(2019年13期)2020-01-14
电子制作(2019年11期)2019-07-04
北京航空航天大学学报(2018年1期)2018-04-20
中国公路(2017年8期)2017-07-21
浙江大学学报(工学版)(2016年11期)2016-06-05
舰船科学技术(2016年1期)2016-02-27

