基于模糊规划的无线传感器网络节点选择方法

涂伟健，徐向华，程宗毛，王 然

(1.杭州电子科技大学 计算机学院，浙江 杭州 310018；2.杭州电子科技大学 理学院，浙江 杭州 310018)

无线传感器网络由许多小型传感器节点组成，每个传感器节点具有采集、处理和转发数据的功能，采集的数据包括温度、湿度、光照强度、电压等。并以其低廉、小型、功能强大的特点被广泛应用于多种场合，比如震动监控[1-3]，精准农业[4-6]、目标检测[7-8]和区域重构[9-11]等。

在针对节点选择问题时，文献[12]设计了一种稀疏选择向量选择最有益的传感器集合来满足克拉美罗界，而克拉美罗界被解释为误差约束。而文献[13]通过将区域网格化，选择满足误差要求的网格点作为节点的部署点。文献[12～13]虽然都考虑了误差精度，将传感器选择问题转化为最优化问题求解，但在选择节点时并有没考虑所选传感器是否能够正常工作，若所选传感器处于故障状态，那么选择的节点子集就不能正常工作。文献[14]针对节点选择问题设计了一种稀疏促进罚函数避免重复选择相同传感器节点，将问题公式化为凸二次规划求解，从而达到网络中传感器节点负载均衡的目的。但是将误差精度作为凸二次规划的目标，会使得最终选择的传感器子集可能出现误差较大的情况。

因此，在节点选择的过程中，节点不仅要满足误差约束要求，而且为了避免选择处于故障状态的节点，还需要考虑节点处于工作状态的概率。在误差约束方面，模糊规划算法选用反距离加权插法对插值点数据进行预测，并利用均方误差评价插值效果。在正常工作概率方面，通过节点采样的历史数据，计算每个节点处于工作状态的概率，在最终选择节点子集的时候，子集中的节点处于正常工作的概率要满足给定的阈值要求。

1 公式化误差约束条件

1.1 误差约束

假设f(tk,sn)表示位置sn上的节点k时刻的采样值。由于采样的过程中会产生误差，表示为ek,n。那么，测量模型公式化为

yk,n=f(tk,sn)+ek,n

(1)

式中，yk,n表示第n个传感器k时刻的真实值。k=1，2，…,k,n=1,2,…,n。ek,n服从正态分布，即ek,n～N(0,σ2)，期望为0，方差为σ2，σ2是噪音的协方差矩阵。令

y=[y1,1,…,yK,1,…,y1,N,…,yK,N]T

(2)

f=[f(t1,s1),…,f(tK,s1),…,f(t1,sN),…,f(tK,sN)]T

(3)

e=[e1,1,…,eK,1,…,e1,N,…,eK,N]T

(4)

分别表示第N个传感器K时刻的真实值，采样值和误差。根据上述公式可以把测量模型简化表示为

y=f+e

(5)

由于目标是区域重构，需要通过控制点对插值点的数据进行插值预测。假设插值点的采样值为θ，坐标为δ。那么插值点的测量模型可以公式化为

θ={f(t1,δ),f(t2,δ),…,f(tk,δ)}

(6)

式(6)中，θ表示坐标δ的传感器节点K时刻测量数据的真实值，f(tk,δ)表示坐标δ的传感器节点在tk时刻的采样值。

由于反距离加权插值是利用控制点和插值点之间的距离来确定权值，特别适合于对温度数据的预测。因此，基于反距离加权插值模型，插值点的测量模型可以公式化为

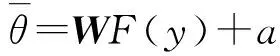
(7)

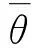
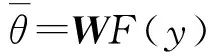
(8)

根据均方误差公式

(9)

再联立插值模型，可得误差公式为

(10)

展开可表示为

(11)

式(11)中，J(w)表示误差精度，接下来需要对该公式进行简化。由于y=f+e，令

E(F(y)F(y)T)=E[F(y+e)F(f+e)T]=P

(12)

E(F(y)θ)=E[F(f+e)θ]=E[F(f)×f(tk,δ)]=q

(13)

(14)

(15)

1.2 反距离加权插值

反距离加权插值法是基于基本假设：两个物体相似性随他们之间的距离增大而减少。它以插值点与控制点间的距离为权重进行加权平均。插值过程主要包括3个步骤：

(1)计算插值点到所有控制点的距离

(16)

式(16)中，(x,y)表示插值点的坐标，(xi,yi)表示控制点的坐标；

(2)计算每个点的权重。权重是距离的倒数的函数，表示为

(17)

λi表示第i个节点的权重，n为控制点数量。p是一个任意正整数，一般令p=2；

(3)计算预测值

(18)

2 公式化节点正常工作概率

在现实情况中，无论是确定性部署还是随机部署，传感器节点会因为各种各样的软件因素或者硬件因素而故障，从而造成节点不能工作。因此在传感器选择问题中需要同时考虑所选传感器尽可能多的处于能够工作的状态。

从历史采样数据中可以得知，传感器节点在当前工作时长中正常工作所占的时间比。假设随机变量s表示节点正常工作的时间，从历史采样数据中可知，s是一个服从几何分布的随机变量，从而可以得到特定传感器的正常工作的概率。

令传感器节点正常工作概率表示为P(si)，P(si)是单个节点正常工作的概率。假设si节点的当前工作总时长为Ta，当前工作总时长中正常工作的时间为Tn，那么P(si)可以表示为

(19)

如果所选的传感器是以集合的形式，那么可以根据容斥公式，多个节点组合的概率可以表示为

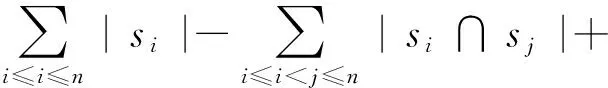
(20)

容斥原理是一种组合数学方法，可以计算复合事件的概率。然而，所选的节点是多个节点的集合，希望集合中至少有传感器节点能够正常工作，而容斥公式正是描述这样一个事件发生的概率。例如，假设选择了节点s1和s2，且s1与s2是相互独立的事件，那么根据容斥公式，其组合概率可以表示为

P(s1+s2)=P(s1)+P(s2)-P(s1)P(s2)

(21)

若所选传感器节点增加，组合概率计算方法可通过式(20)计算。

3 模糊规划

本文算法将误差精度和工作概率公式化为约束条件，将最小化选择的传感器数量作为目标函数，把传感器选择问题首先转化为0-1整数规划问题求解。

令布尔变量wn表示第n个传感器节点，当wn=1时表示选择第n个传感器节点，反之，当wn=0时表示不选择。那么根据最小化选择的传感器数量的目标，可以得到目标函数为

min‖wn‖0,1

(22)

另外，根据上述公式化的约束条件，将节点选择问题转化为0-1整数规划问题求解。

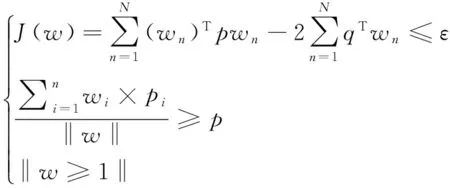
(23)

式(23)中，ε和p分别为给定的误差精度阈值和节点正常工作的概率阈值。

普通线性规划的约束条件都是确定的，但在一些实际问题中，约束条件可能带有弹性，必须借助模糊集的方法来处理。

为了更具一般性，算法将0-1整数规划推广到模糊线性规划。普通线性规划的约束条件表示为

ti(x)=bi

(24)

式(24)中，x=[x1,x2,…,xn]，ti=ai1x1+ai2x2+…+ainxn，bi为常数阈值。若将约束条件转换为模糊函数，则表示成

ti(x)=[bi,di]

(25)

式(25)中，di称为伸缩指标，当di=0时，模糊规划就退化成线性规划。当di>0时，ti(s)取[bi-di,bi+di]内的某一个值。最终，可将节点选择问题转化为模糊规划求解。

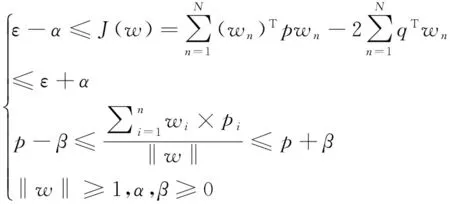
(26)

式(26)中，α、β为相应的伸缩指标。

4 仿真实验

利用Intel Berkeley 实验室的数据集[15]对0-1整数规划和模糊规划分别进行实验对比。数据集记录了从2004年2月28日～4月5日的温度、湿度、光照强度和电压的数据，区域中共部署了54个传感器节点，随机选取8个节点的温度数据对算法模拟实验。实验平台为Microsoft Visual Studio 2010。

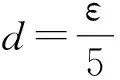
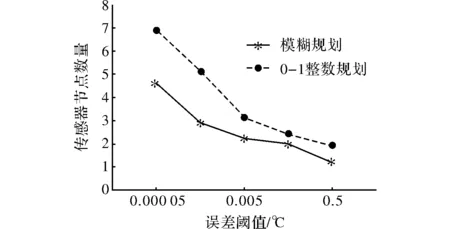
图1 模糊规划与0-1整数规划对比

图2和图3分别显示了概率阈值和伸缩指标对选择的节点的数量的影响。从图2中可以看到，随着概率阈值的提高，算法需要选择更多的传感器节点来增加正常工作概率，所以传感器节点数量随概率阈值的增加而增加。另外，误差阈值越小，需要选择的传感器节点数量越多。

在图3中，由于伸缩指标是作为误差阈值的一部分，伸缩指标的放大，相当于增加了误差阈值，因此选择较少的节点数量既能满足阈值要求。所以在图3中，传感器节点数量随伸缩指标的增加而减少；另一方面，概率阈值越大，选择的传感器节点数量也越多。

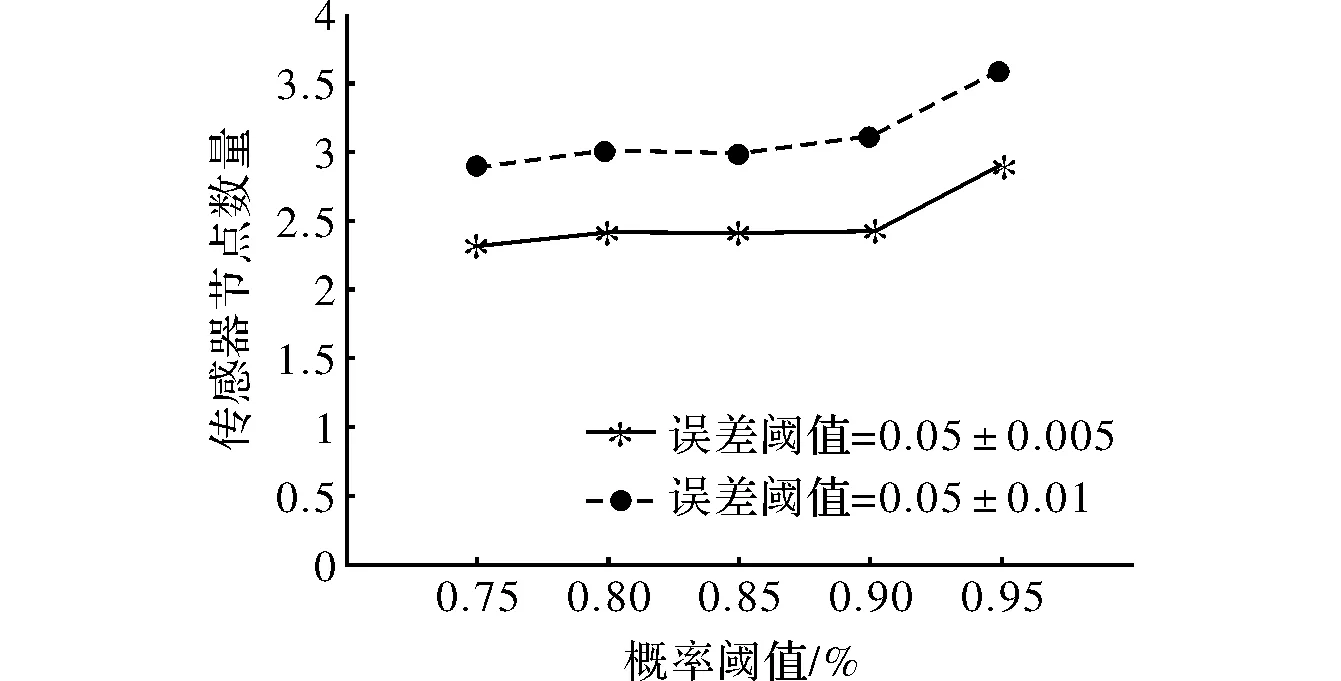
图2 概率阈值对节点数量的影响

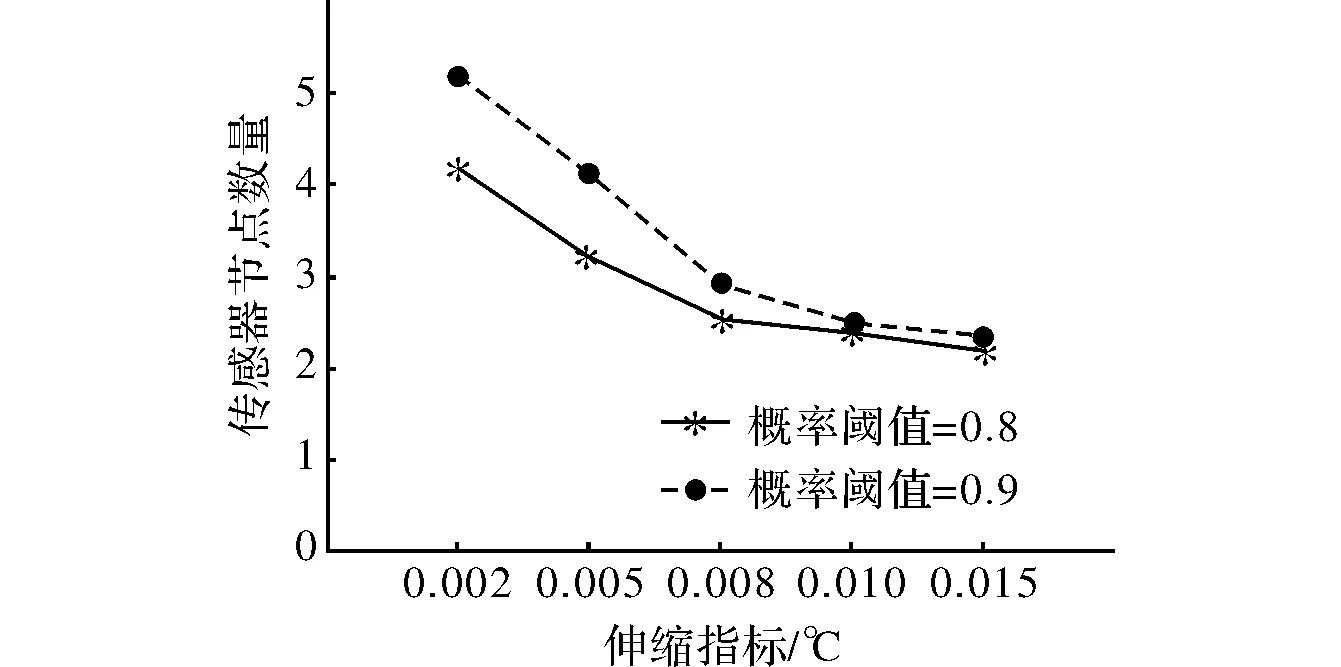
图3 伸缩指标对节点数量的影响

5 结束语

本文提出了一种基于模糊规划的节点选择算法。以误差精度和工作概率作为约束条件，以最小化所选的节点数量为目标，将节点选择问题转化为0-1整数规划求解，并且将0-1整数规划进行一般性推广，转化为模糊规划。最后，利用温度数据集对提出的两种方法进行仿真实验，结果显示两种方法能明显减少所选的节点数量，并且模糊规划要优于0-1整数规划。

[1] Barooah P,Chenji H,Stoleru R,et al.Investigation of wireless sensor networks for structural health monitoring[J].Journal of Sensors,2012,2012(1):276-283.

[2] Gao S,Yuan S,Qiu L,et al. A high-throughput multi-hop WSN for structural health monitoring[J].Journal of Vibroengineering,2016,18(2):781-800.

[3] Hackmann G,Guo W,Yan G,et al. Cyber-physical codesign of distributed structural health monitoring with wireless sensor networks[J].IEEE Transactions on Parallel and Distributed Systems,2014,25(1):63-72.

[4] Wang B,Deng X,Liu W,et al.Confident information coverage in sensor networks for field reconstruction[J].IEEE Wireless Communications,2013,20(6):74-81.

[5] Brinis N,Saidane L A.A wireless sensor network in precision agriculture[J].Wireless Sensor Network,2016,8(1):1-12.

[6] Anisi M H,Abdul-Salaam G,Abdullah A H. A survey of wireless sensor network approaches and their energy consumption for monitoring farm fields in precision agriculture[J].Precision Agriculture,2015,16(2):216-238.

[7] 魏鹏,路赞赞.无线传感器网络分布式多传感器目标检测[J].电子科技,2014,27(3):143-146.

[8] Shahbazian R,Ghorashi S A.Distributed cooperative target detection and localization in decentralized wireless sensor networks[J].Journal of Supercomputing,2016(8):1-18.

[9] Sijia Liu,Vempaty A,Fardad M,et al. Energy-aware sensor selection in field reconstruction[J].IEEE Signal Processing Letters,2014,21(12):1476-1480.

[10] Santini S,Colesanti U.Adaptive random sensor selection for field reconstruction in wireless sensor networks[C].Lyon:The Workshop on Data Management for Sensor Networks, in Conjunction with Vldb,2009.

[11] Joshi S,Boyd S.Sensor selection via convex optimization[J].IEEE Transactions on Signal Processing,2009,57(2):451-462.

[12] Chepuri S P,Leus G.Continuous sensor placement[J].IEEE Signal Processing Letters,2015,22(5):544-548.

[13] Chepuri S P,Leus G.Sparsity-promoting adaptive sensor selection for non-linear filtering[C].MA,USA:IEEE International Conference on Acoustics, Speech and Signal Processing,2014.

[14] Liu S,Masazade E,Fardad M,et al. Sparsity-aware field estimation via ordinary Kriging[C].CA,USA:IEEE International Conference on Acoustics, Speech & Signal Processing,2014.

[15] Madden S.Intel lab data[EB/OL]. (2004-01-02) [2015-12-18] http://db.csail.mit.edu/labdata/labdata.html.