激光辐照材料热效应问题的有限元实现

徐 鹏，韩一平

(西安电子科技大学 物理与光电工程学院，陕西 西安 710071)

激光技术已被应用在生活中的许多方面，研究激光与材料间的热效应可以不断提高材料的抗激光损伤能力，为推广激光技术在科研及生产中的应用具有重要研究价值。

文献[1～10]对激光辐照光学材料热效应问题进行了解析计算及有限差分数值计算，其所研究材料模型相对实际应用模型有所简化。文献[11～13]是用有限元软件计算激光辐照材料的温度场和应力场，较少有自行编写有限元法求解程序。本文拟根据有限元理论推导六面体单元的有限元格式，编制求解任意形状三维模型材料的温度场程序，并对光学透镜在激光辐照下的温度场分布问题进行研究。

1 光学透镜模型的有限元分析

激光对材料的辐照作用[14-17]可以理解为材料吸收激光的能量转化为热能继而向周边介质进行热扩散。因此可以将激光等效为材料的一个热源函数，研究热量在材料中的热传导问题。对于光学透镜模型，在圆柱坐标系下，定义瞬态温度场为T(r,z,t)，则物体内部 的热交换可用以下的热传导方程来描述。

(1)

式中，T(r,z,t)表示在时间t时的温度分布；ρ,c,k分别为密度、比热和热传导系数，I(r,z,t)为激光热源函数。假定被加热材料是各向同性物质，材料的热物理参数与温度无关，在材料的激光入射面存在与空气的对流冷却，其它边界均被设为热绝缘，初始温度为239 K。采用脉冲激光，激光热源函数的空间分布采用高斯分布，所以材料所吸收的能量可表示为

I(r,z,t)=α(1-R)I0f(r)m(z)g(t)

(2)

(3)

m(z)=exp(-αz)

(4)

(5)

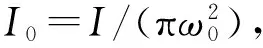
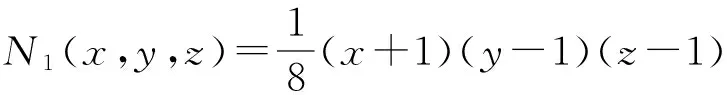
(6)

为了适应于任意形状三维模型的求解，采用单元的等参变换得到非规则六面体单元矩阵的表示式为

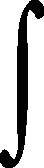
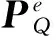
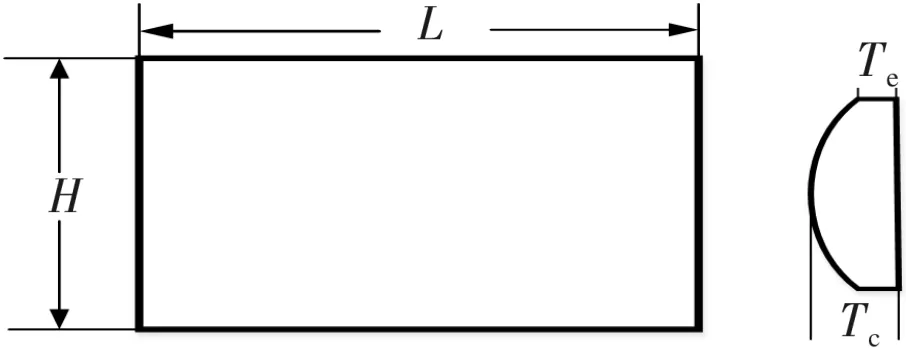
图1 光学透镜截面示意图

图1中L和H分别为光学透镜的高8 mm和宽4 mm，Tc和Te分别为光学透镜的边厚3.8 mm和中心厚度2 mm。假设激光从光学透镜的矩形表面正入射，方向取为Y轴，沿着L方向为Z轴方向，沿着H方向为X轴方向。激光光斑中心与材料被入射表面中心重合，所采用的激光参数为激光脉冲宽度为1 ms，重复频率为100 Hz，光斑半径为1 mm和0.5 mm，激光波长为1 064 nm，脉冲平均功率为50 mW，材料表面反射系数R取90%，所选用的材料为石英玻璃，石英玻璃的熔点为1 750 ℃。

2 温度场结果分析

2.1 激光光斑半径对温度场的影响

图2为激光辐照中心沿Y轴方向的温度曲线图，图3为激光辐照中心沿Z轴方向的温度曲线图，图4为激光辐照中心沿X轴方向的温度曲线图。

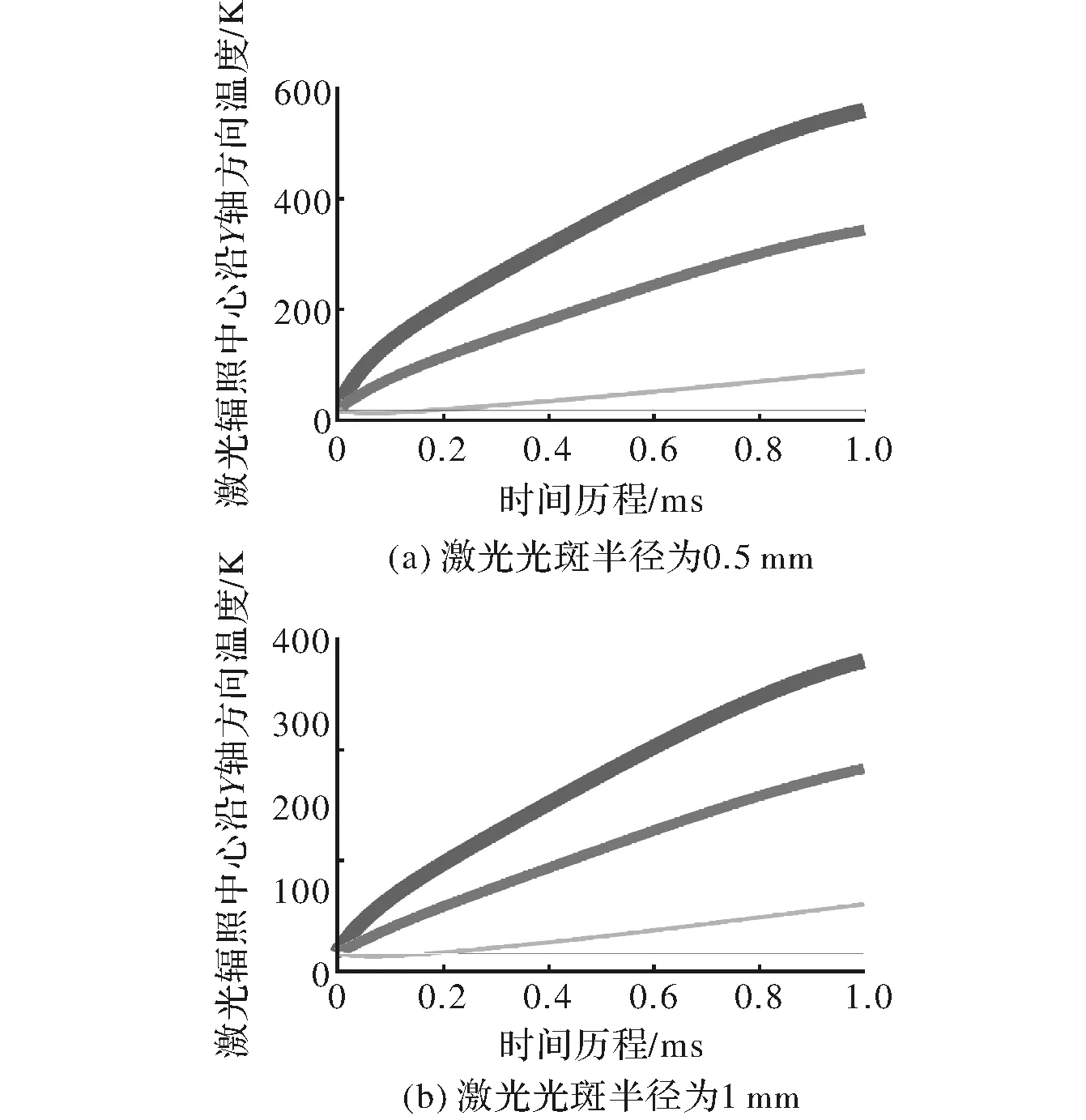
图2 激光辐照中心沿Y轴方向的温度分布曲线

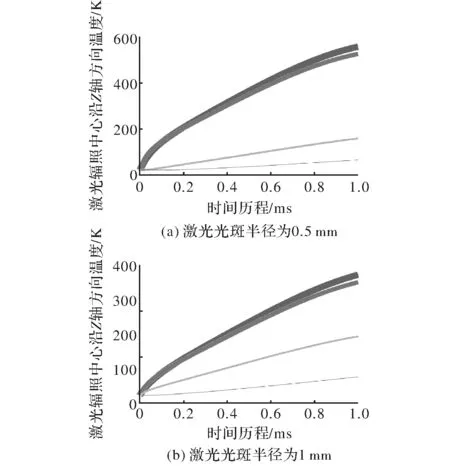
图3 激光辐照中心沿Z轴方向的温度分布曲线

图2(a)、图3(a)和图4(a)分别为激光光斑半径为0.5 mm时由上到下(即线宽由大到小)依次为激光辐照中心点、激光辐照中心沿Y轴方向、沿Z轴方向和沿X轴方向距离中心点0.5 mm、1 mm、1.5 mm的温度曲线。图2(b)、图3(b)和图4(b)为激光光斑半径为1 mm时的温度曲线。对比图2(a)和图2(b)、图3(a)和图3(b)以及图4(a)和图4(b)可以发现相同的规律，即光斑半径为1 mm时无论是激光中心点还是中心点沿Y轴、Z轴和X轴方向的温升都要低于光斑半径为0.5 mm时的情况。这是由于在激光总能量不变的情况下，随着激光光斑半径的增大，激光能量更分散，激光的峰值能量即光斑中心的能量随之减少。对比图2(a)和图3(a)可以得到，在同一激光光斑半径下，材料沿Y轴方向离辐照中心点相同距离的位置点的温升要低于沿Z轴方向和沿X轴方向，分析原因可知材料沿Y轴方向造成温度升高的热量来自于材料表面吸收的激光能量的热传导过程，而沿Z轴方向和沿X轴方向的同一位置可能处于激光辐照区，其热量直接来自于材料对辐照激光热量的吸收，所以温度升高的更快。而且沿Y轴方向的温度梯度要小于Z轴，从热弹性理论可知在激光辐照结束后，最先遭到应力破坏的是材料表面，因为材料表面温度梯度更大，将产生的应力也更大。对比图3(a)和图4(a)，可以分析得到距离激光辐照中心相同距离的位置沿Z轴方向的温升要高于X轴方向，分析可知原因是激光的分布形式为高斯分布，并不是均匀分布，沿Z轴方向获得更多的激光能量。

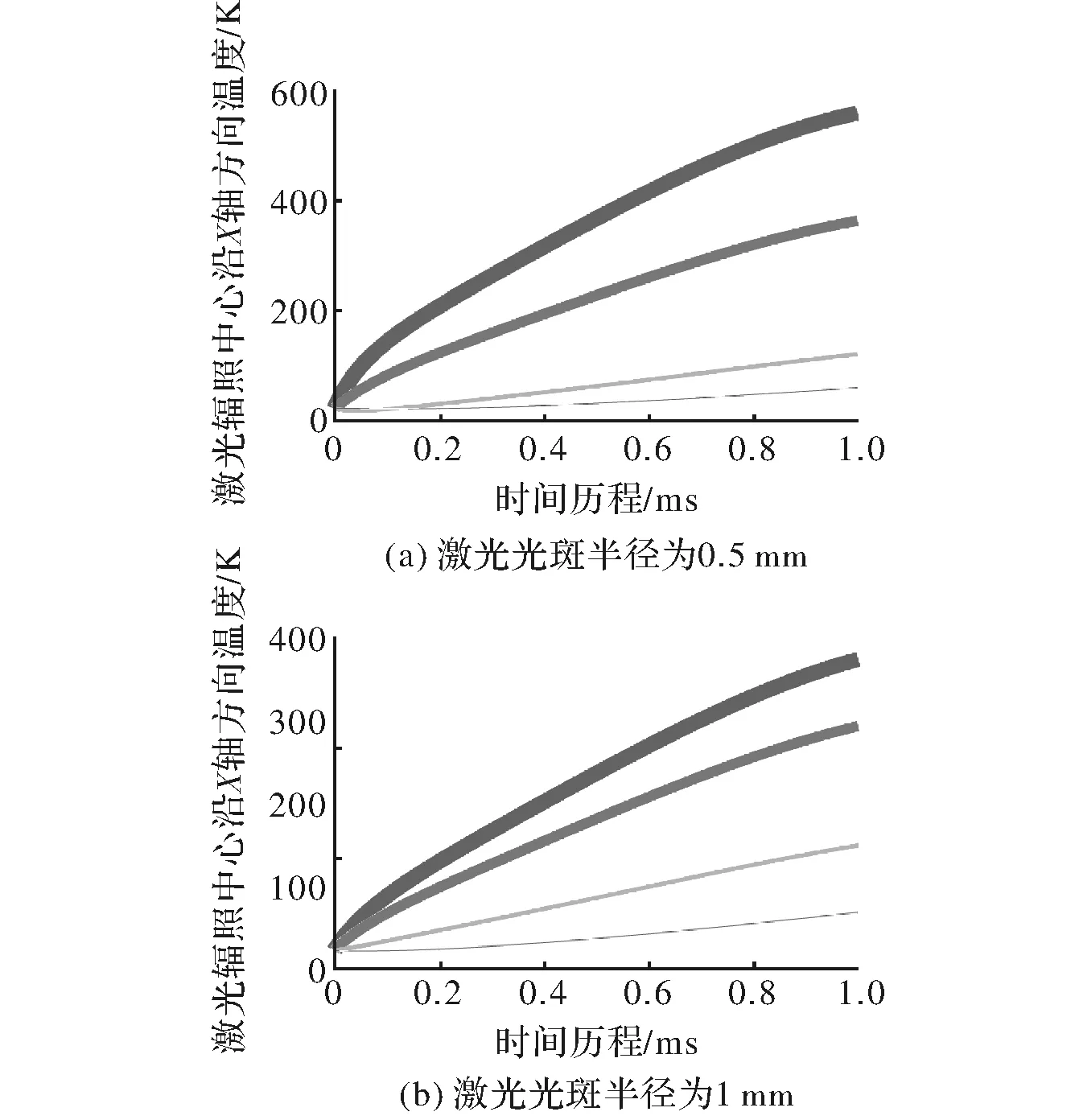
图4 激光辐照中心沿X轴方向的温度分布曲线

2.2 激光功率对温度场的影响

图5是不同激光功率下的激光能量密度图，可知在同等条件下，激光能量随激光功率的增大而增大。图6为不同功率的激光作用下，激光辐照中心点的温度曲线图。由图中可以看出，激光辐照中心的温度随激光功率的增大而增大，当激光功率为250 mW时，最高温度大约已到石英玻璃的熔点1 750℃，当激光功率为300 mW 时，材料的温度大约在0.75 ms时已经达到熔点，即会造成材料的熔融损伤，此时一个激光脉冲尚未结束。由此可知，石英玻璃的抗熔融损伤的激光功率阈值为250 mW。

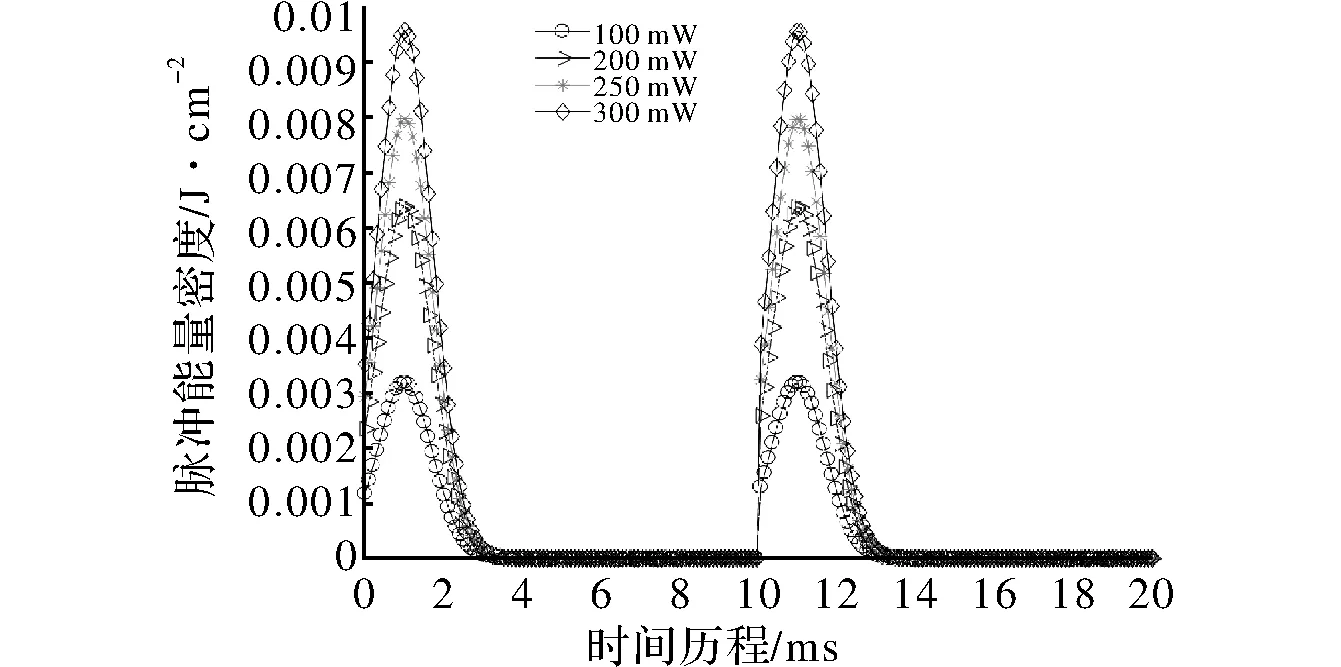
图5 不同激光功率下的脉冲能量密度图

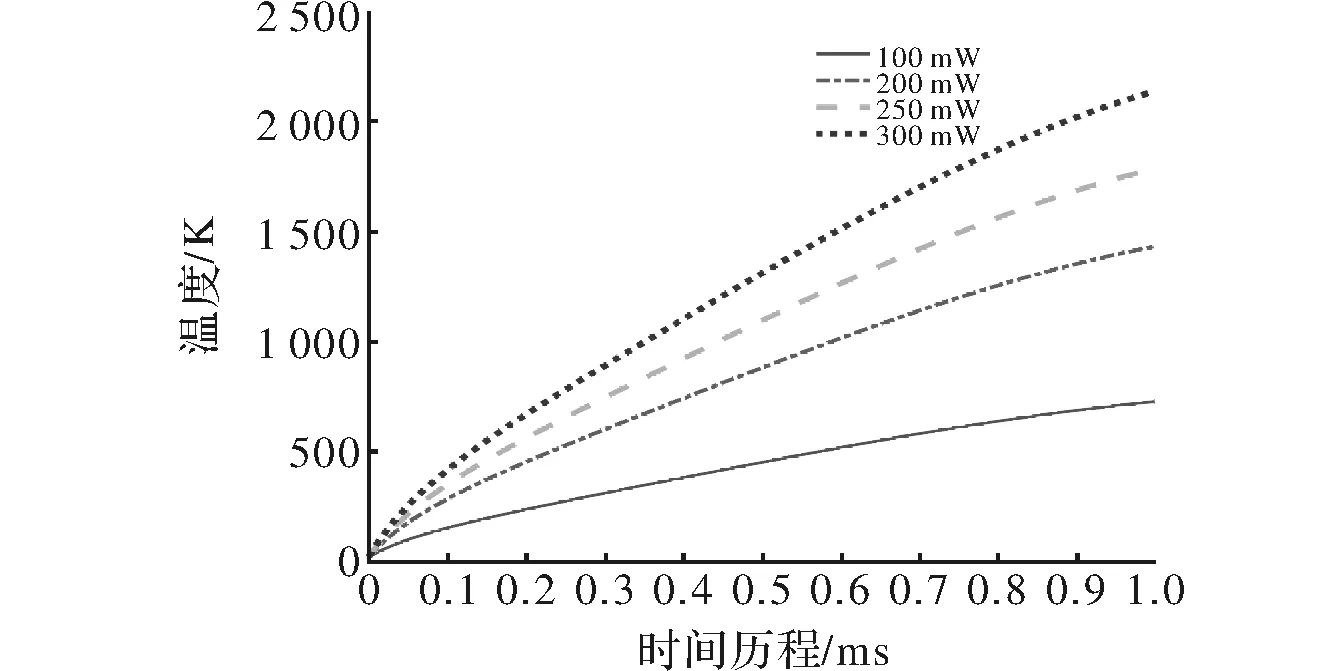
图6 不同激光功率下激光辐照中心点的温度曲线

2.3 激光脉冲个数对温度场的影响

图7是激光光斑半径为1 mm，脉冲功率为100 mW，3个脉冲作用下材料不同位置的温度曲线图，从图中可以看出，图7(a)激光辐照中心点和图7(b)沿Z轴方向的温度先升高后减小，1 ms时第一个脉冲激光作用结束，中心点的温度达到最大值，然后逐渐下降，因为激光脉冲作用结束后，热量通过热传导过程向周围介质扩散。第二个激光脉冲作用后，激光辐照中心点的温度最大值要高于第一个激光脉冲作用后的温度，这是由于激光脉冲能量的累积效应导致了材料温度最大值的增大。第三个脉冲具有同样的作用规律，由此可知，随着脉冲数目的增加，材料的温度由于激光能量的累积效应逐渐升高，在某一时刻材料的温度终会高于其熔点造成材料的熔融损伤。

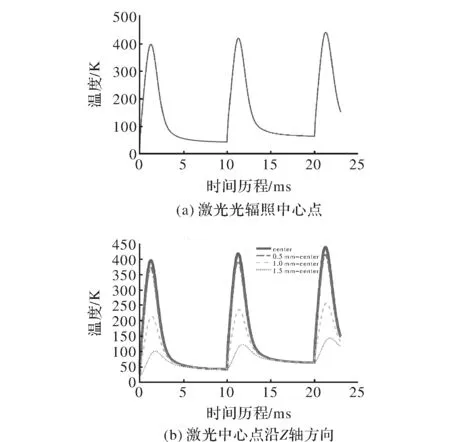
图7 激光光斑半径1 mm时不同位置温度曲线

3 结束语

本文通过自编有限元法程序对光学透镜的温度场进行了计算，分析脉冲激光参数对材料温度场影响的过程中，发现激光功率是最直接的影响因素，当激光功率为250 mW 时，将造成石英玻璃的熔融损伤，该数值可以为激光加工提供参考。研究温度场时未考虑材料属性随温度的变化，也尚未研究材料的应力场分布问题，可以作为今后的研究方向。

[1] 蒋志平,陆启生,刘泽金.强激光辐照下InSb(PV)型探测器的温升计算[J].强粒子与激光束,1990,2(2):247-251.

[2] 沈中华,陆建,倪晓武.硅材料在强激光作用下的二维温升模拟计算[J].南京理工大学学报,1998,22(3):80-83.

[3] 段晓峰,汪岳峰,牛燕雄等.激光辐照光学材料热力效应的解析计算和损伤评估[J].中国激光,2004,31(12):1455-1459.

[4] 牛燕雄,张书练,姚建铨等.高功率激光对光电器件的热—力破坏效应[J].激光与光电子学进展,2007,44(8):32-42.

[5] 崔云霞,牛燕雄,王彩丽.连续激光辐照锗材料损伤的数值模拟研究[J].应用光学,2011,32(2):267-271.

[6] 邓素辉.激光与物质相互作用的热效应研究[D].南昌:江西师范大学,2006.

[7] 李川.激光对光电材料的损伤探究[D].西安:西安电子科技大学,2010.

[8] 罗福,杜祥琬,孙承纬.光斑尺寸对K9玻璃近红外激光损伤阈值的影响[J].爆炸与冲击,2002,22(1):61-65.

[9] 王玺,方晓东.K9玻璃在脉冲CO_2激光作用下的热应力分析[J].强激光与粒子束,2014,26(5):38-41.

[10] 连祖焻,赵抒怡,叶云霞.飞秒激光作用下金属箔材的温度场研究[J].电子科技,2016,29(1):22-26.

[11] 孟冬冬,伍彦伟,范彩连,蔡野.基于体热源的激光透射焊接PA66温度场模拟[J].电子科技,2016,29(1):17-22.

[12] 袁红.激光辐照下旋转柱壳温度场的数值模拟[J].强激光与粒子束,2005,17(5):681-684.

[13] 马建.基于有限元的脉冲激光辐照材料温度场研究[J].激光与红外,2015,45(1):27-31.

[14] 胡昌信.强激光与物质的相互作用[J].力学进展,1980(Z1):118-128.

[15] 周益春,段祝平,解伯民.强激光破坏机制研究进展[J].力学与实践,1995,17(1):10-18.

[16] 郑启光,辜建辉.激光与物质相互作用[M].武汉:华中科技大学出版社,1996.

[17] 孙承伟,陆启生,范正修.激光辐照效应[M].北京:国防工业出版社,2002.

[18] 王勖成.有限单元法[M].北京:清华大学出版社,2003.