基于压缩感知的阅卷系统手写汉字识别算法

郑昊辰，姜 维

(1.中国人民大学 附属中学,北京100080;2.华北水利水电大学 软件学院,河南 郑州 450045)

阅卷系统是现代化教学过程中评估教学效果的重要工具，手写汉字识别是阅卷系统的重要组成部分[1-3]。精准、高效的手写汉字识别算法能够大幅提高阅卷系统的准确度和便捷性。但是由于汉字识别存在类别多、结构复杂、相似字多、书写差异大[4-8]等问题，手写汉字识别算法已成为制约阅卷系统发展的瓶颈。虽然经过多年的研究，汉字识别已经有了许多成果，但其在实际应用中的性能仍需改善。对于无约束的手写汉字识别，尚无简单的方案能满足高识别率和识别精度的要求[9]。近年来，研究人员主要从两个方向对汉字识别方法进行改善：(1)运用神经网络、隐马尔可夫、支持向量机(Support Vector Machine，SVM)、数学形态学等方法进行预处理、特征提取和分类；(2)采用信息集成的方式从多角度对手写字符进行综合分析[10]。

在信息处理领域，关于超完备基的稀疏线性表示计算问题，即压缩传感理论(Compressive Sensing，CS)是近年来的研究热点之一[11-12]。压缩感知理论也可应用在模式识别问题上，文献[13]将训练样本作为超完备基，利用稀疏表示的判别性实现了人脸识别。若每类样本足够充分，则测试样本可表示为同类样本的线性组合，对于整个样本集而言，其表示是非常稀疏的，使得分类问题可通过压缩感知的方法来实现。文献[14]同样利用这种方法，对手写数字进行了有效的识别。本文基于上述思想，将压缩感知理论应用到更为困难的手写汉字识别领域。

1 压缩感知

压缩感知理论最早被应用在信号处理领域[15]。与传统的奈奎斯特采样定理不同，压缩感知理论认为信号的采样速率并不仅仅局限于其带宽，还与信号的内容有很大关系。只要信号是可压缩的或在某个变换域是稀疏的，那么就可以用一个与变换基不相关的观测矩阵将变换所得的高维信号投影到一个低维空间上。若通过求解一个优化问题就可以从这些少量的投影中以高概率重构出原信号，则证明该投影包含了重构信号的足够信息。

从上面压缩感知理论的基本描述可以看出，该理论有三个要点要解决：(1)稀疏的概念；(2)观测矩阵的选取；(3)如何求解该优化问题。这三点也构成了压缩感知理论研究的主体框架。

1.1 稀疏的概念

从傅立叶变换到小波变换再到后来兴起的多尺度几何分析，科学家们的研究目的均是为了研究如何在不同的函数空间为信号提供一种更加简洁、直接的分析方式，所有这些变换都旨在发掘信号的特征并稀疏表示它,或者说旨在提高信号的非线性函数逼近能力，进一步研究用某空间的一组基表示信号的稀疏程度或分解系数的能量集中程度。

稀疏的数学定义为：信号X在正交基Ψ下的变换系数向量为Θ=ΨTX，假如对于00，若这些系数满足

(1)

则说明系数向量Θ在某种意义下是稀疏的。稀疏的另一种定义为：若变换系数θi=〈x,Ψi〉的支撑域{i：θi≠0}的势小于等于K，则信号X是K项稀疏。如何找到最佳的稀疏域，是压缩感知的基础和前提，也是重要的研究方向。

1.1 观测矩阵的选取

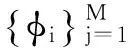
y=φΘ=ΦΨTX=ACSX

(2)

对于给定的Y从式(2) 中求出Θ是一个线性规划问题，但由于M≪N，即方程的个数少于未知数的个数，这是一个欠定问题，一般来讲无确定解。然而，如果Θ具有K项稀疏性(K≫M)，则该问题有望求出确定解。此时，只要设法确定出Θ中的K个非零系数θi的合适位置，由于观测向量Y是这些非零系数θi对应Φ的K个列向量的线性组合，从而可以形成一个M×K的线性方程组来求解这些非零项的具体值。

1.2 信号重构

求解一个优化问题，可以从少量的投影中以高概率重构出原信号，即为信号重构问题。在压缩感知理论中，由于观测数量M远小于信号长度N，因此不得不面对求解欠定方程组Y=ACSX。表面上看，求解欠定方程组似乎是无望的，但是由于信号X是稀疏的或可压缩的，这个条件从根本上改变了问题，使得问题可解。

为更清晰地描述压缩感知理论的信号重构问题，首先定义向量X={x1,x2,…,xn} 的p-范数为

(3)

当p=0时得到0-范数，它表示X中非零项的个数。在信号X稀疏或可压缩的前提下，求解欠定方程组Y=ACSX的问题转化为最小0-范数问题

min‖ΨTX‖0s.t.ACSX=ΦΨTX=Y

(4)

但是0-范数问题是一个NP-hard的问题，但求解l1优化问题可以得到近似的解，从而使得该问题可解。

2 压缩感知在手写汉字识别的应用

手写汉字识别过程本质上是确定当前输入的样本与训练样本之间的对应关系。[7]假定系统的类别为K，每个类别对应的训练样本为N1，N2，…，Nk。对应于类别i，其特征矩阵Ai={vi1,vi2, …,viNi}，则对于属于i类的输入测试样本Y，有Y=k1×vi1+k2×vi2+…+kNi×viNi。所以在识别过程中，在类别未知的情况下，可以表述为Y=0×v11+…+ 0 ×vi-1,Ni-1+k1×vi1+k2×vi2+…+kNi×viN+0×vi+1,1+…+0×vK,Nk，ki,j∈R。

对于上述问题可以有如下表达

Y=Ax

(5)

对于待分类样本Y，x为稀疏系数，x=(k11,k12, …,kK,Nk)T,A为观测矩阵，A=(A1,A2, …,AK)=(v11,v12, …,vK,Nk)。

为了用稀疏系数x来表达Y，需要求解式(5)。式(5)中，A为M×N矩阵，其中N≫M，所以方程(5)是一个欠定方程组，有无穷组解。用最小l1范数来约束该问题，即

Y=Ax
s.t.x=arg min ||x||1

(6)

在得到稀疏系数x后，用一个函数Ti(x)来计算用第i类恢复出来的Yi，Yi=ATi(x)其中

Ti(x)={0,0,…,ki1,ki2,…,kiNi,0,…,0}

(7)

最后分类用最小残差来分类，即

minri(yi)=min‖y-AT(xi)‖

(8)

用压缩感知进行手写汉字识别的流程图如图1所示。

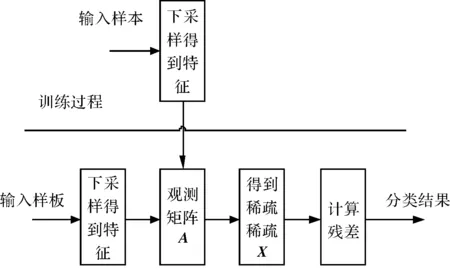
图1 算法流程图

3 实 验

为了验证算法的有效性，本文提出的方法在ETL9B[16]手写汉字库上进行实验。ETL9B由日本JAIST采集，包含3 036个类别，每个类别由200个人书写。图2是该数据库中的部分样本示意图。

图2 ETL9B样本示意

首先对原始的文字图像进行采样，得到16×16 的图像，然后将其直接拉伸成一个256维的一维向量，再用所有的训练样本组成观测矩阵A。在识别过程，用待识别样本在最小l1范数下计算稀疏系数x，利用式(8)得到分类结果。

为简化实验，本文选取2 965个汉字的200个类别用于实验，图3是测试样本的稀疏系数。表1为本文算法在该数据集上的实验结果，可以看出，提出的方法可以有效鉴别文字图像的类别信息。

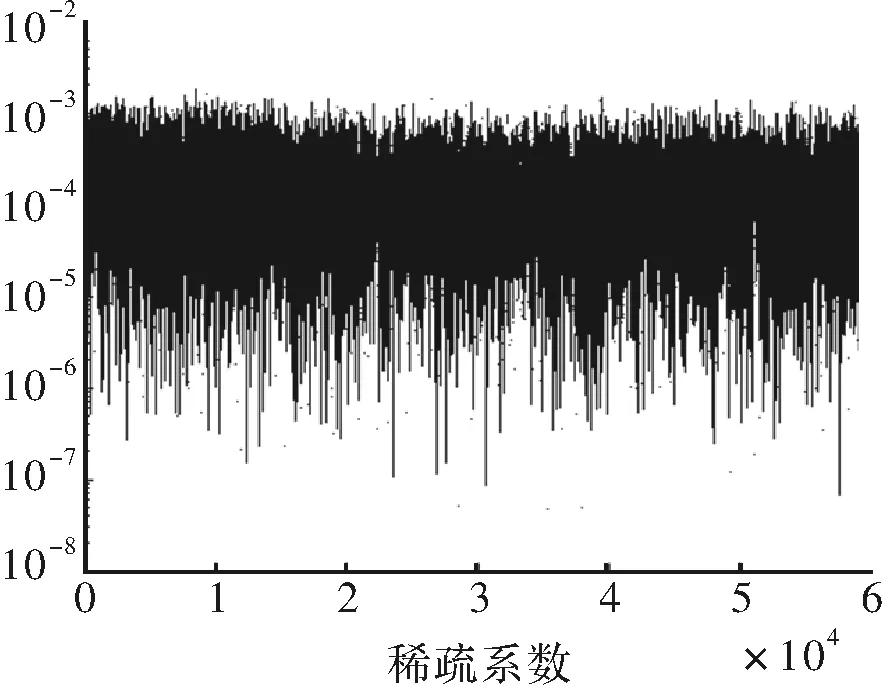
图3 稀疏系数示意图

最近中心最近邻本文方法识别率97.2%98.9%99.1%

其中，最近中心(Nearest Mean，NM)是用待分类样本与每个类别中心点的欧式距离来判断样本的类别。最近邻(Nearest Neighbor，NN)是用待分类样本与每个类别的中心点的欧式距离来判断样本的类别。

4 结束语

本文提出的方法用对信号的随机采样替代了传统的特征提取方法，简化了算法的实现过程；另外，新方法用所有的训练样本组成训练字典，避免了复杂的训练过程。在手写汉字数据库ETL9B上的实验结果表明提出方法的有效性。未来工作的研究重点将放在如何构建新的构建观测矩阵，以节省存储空间提升计算效率。

[1] 田香玲,席志红.压缩感知观测矩阵的优化算法[J].电子科技,2015,28(8):102-111.

[2] 任越美,张艳宁,李映.压缩感知及其图像处理应用研究进展与展望[J].自动化学报,2014,40(8):1563-1575.

[3] Lu W, Liu Y Z,Wang D S.Efficient feedback scheme based on compressed sensing in MIMO wireless net works[J].Computers and Electrical Engineering,2013,39(6):1587-1600.

[4] 阮涛,那彦,王澍.基于压缩感知的遥感图像融合方法[J].电子科技,2012,25(4):43-46.

[5] 杜卓明,耿国华,贺毅岳.一种基于压缩感知的二维几何信号压缩方法[J].自动化学报,2012, 38(11): 1841-1846.

[6] Liang S, Wang Y, Liu Y. Face Recognition Algorithm Based on Compressive Sensing and SRC[C].Guangzhou:Second International Conference on Instrumentation, Measurement, Computer, Communication and Control,IEEE Computer Society, 2012.

[7] 何楚,刘明,冯倩,等.基于多尺度压缩感知金字塔的极化干涉SAR图像分类[J].自动化学报, 2011, 37(7):820-827.

[8] Arica Nafiz,YarmanVural,Fatos T. An overview of character recognition focused on off-line handwriting[J].IEEE Transactions on Systems, Man and Cybernetics,2001,31(2):216-233.

[9] Fujisawa H.Forty years of research in character and document recognition-an industrial perspective[M].Amsterdam:Elsevier Science Inc.,2008.

[10] Dai R,Liu C,Xiao B.Chinese character recognition :history, status and prospects[J]. Frontiers of Computer Science in China,2007, 1(2):126-136.

[11] Cand E J,Wakin M B. "People Hearing Without Listening:" an introduction to compressive sampling[J].IEEE Signal Processing Magazine, 2008,25(2):21-30.

[12] Romberg J.Imaging via compressive sampling [J]. IEEE Signal Processing Magazine, 2008, 25(2):14-20.

[13] Yang A Y, Wright J, Ma Y, et al. Feature selection in face recognition: a sparse representation perspective[J].IEEE Signal Processing Magazine, 2007,24(7):97-109.

[14] 刘长红,杨扬,陈勇.基于压缩传感的手写字符识别方法[J].计算机应用, 2009, 29(8):2080-2082.

[15] 石光明,刘丹华,高大化,等.压缩感知理论及其研究进展[J].电子学报, 2009,37(5):1070-1081.

[16] Saito T, Yamada H, Yamamoto K. On the data base ETL9 of handprinted characters in JIS Chinese characters and its analysis[J].IEICE Transactions,1985, 68(4):757-764.