基于正交匹配追踪算法的语音信号重构研究

陈 益，李文钧

(杭州电子科技大学 电子信息学院，浙江 杭州 310018)

上世纪以来，奈奎斯特采样定理[1]支配着所有的信息传输、处理及存储。若要不失真地重构出原信号，采样频率必须不小于奈奎斯特频率的两倍[2]。但由于采样频率越来越高，计算量越来越大，导致硬件的处理速度难以满足现代人对信息处理的要求。

2006年美国斯坦福大学的Donoho和Candes从信号的分解和逼近理论提出了压缩感知(Compressed Sensing,CS)[3]。压缩感知理论认为：若信号在某一个变换域上是可压缩的或者稀疏的，则可利用一个与它的变换基不相关的观测矩阵将其变换而得到的高维度的信号投影到一个低维度的空间上，根据少量的观测值，通过求解其优化性的问题，并可从少量的投影中以非常高的概率重构出原始信号。

目前，压缩感知理论在许多领域获得广泛的应用研究，如医学图像处理、CS雷达、图像采集设备开发等。目前，针对语音信号的CS理论研究尚处于刚起步的阶段。Gemmeke和Granen利用CS技术原理对有噪声的环境下的语音信号进行识别，实验证明，识别系统的抗噪声性能得到很大提高，显示出CS技术在语音信号处理中的巨大前景[4]。进一步说，如果利用CS技术进行采样，所需采样的数据量将大为减少，再结合有损编码技术，即可以实现更低码率上的高质量语音编码。

本文提出基于正交匹配追踪算法(OMP)[5]的压缩感知重构算法实现对语音信号进行信号重构。仿真实验表明，相比于传统的压缩感知的重构算法，本方法对含噪语音的去噪效果也会更好，重构语音的效果会更高。

1 压缩感知

压缩感知以信号的稀疏表示为基础，通过求解欠定线性方程组的最优化问题进而来实现对信号重构，观测矩阵、稀疏变换基和恢复算法是其三大要素。压缩感知是一种新的能够在采样的同时实现压缩目的的技术。其压缩的采样过程可以分成3个步骤，其理论框图如图1所示。

首先，如果一个信号X∈RN在某个正交基上或者是在一个紧框架ψ上是能够被压缩的或者是稀疏的，就可以求出它的变换的系数θ=ψTX，θ是ψ的等价或逼近性的稀疏性示[6]；

其次，设计构造一个既平稳又与变换基ψ不相干的，而且是M×N维度的观测型的矩阵Φ，对θ进行观测可以得到一个观测矩阵Y=Φθ=ΦψTX，此过程也可以表示：信号X通过矩阵ACS进行的非自适应性的观测：Y=ACSX，其中ACS=ΦψT，ACS称为CS信息算子[7]；

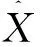
min‖ψX‖0s.t.ACSX=Y

(1)

图1 压缩感知理论框图

图1中，第一步、第二步为低速压缩采样Y=ACSX。压缩感知(CS)理论主要涉及以下几个关键性的问题：(1)对于信号X∈RN，怎样去找到某个紧框架ψ或者是正交基，使其在变换基ψ上的表示是稀疏性的，即信号的稀疏性的表示问题；(2)构造一个平稳且与变换基ψ不相关的M×N维度的观测矩阵Φ，确保稀疏向量θ从N维降到M维时，其重要的信息不会被破坏，即信号的低速型采样的问题[8]；(3)关于如何设计快速性的重构算法，从线性观测Y=ACSX中恢复信号，也即信号的重构问题。

2 基于正交匹配追踪算法的语音信号处理

2.1 语音信号的Matlab生成及其稀疏表示

本文先以原始语音信号为例，如图2所示。通过Matlab实现了生成用于算例的语音观测信号图，图3所示为基于Matlab的压缩感知算法实现的原测试信号观测结果图。线性预测(Linear Prodiction，LP)分析是语音信号处理的核心技术之一。在语音编码、识别以及合成等语音处理领域都有广泛应用。在AR(Autog Ressive)模型中，由于有语音样点之间存在相关性的原因，所以一个语音信号的抽样值x(n)可以用过去的p个取样值的线性组合来逼近

(2)

其中，ai是预测系数；e(n)是自回归滤波器的激励。通过最小均方误差(Least Mean Square，LMS)准则，可以使得语音信号采样值与线性预测值最小，也可以确定唯一的一组线的预测系数{ai}。由上式可以得到LP分析残差e(n)为

(3)

可以将残差写成向量的形式e=Tx。其中

(4)

由上述LP分析可知，浊音残差信号e是以基音周期为周期重复的单位脉冲的序列，也即残差信号仅在基音周期的整数倍的位置上才会有较大的幅值。这进一步说明了，矩阵T确实是去除了语音信号x在相邻样点之间的相关性，所以此时将矩阵T称为分析矩阵。语音信号也可近似的表示为

x=R-1e=He

(5)

其中，H为分析矩阵T的逆矩阵T-1，将残差信号e映射到语音信号域进而实现信号的重构，所以将H矩阵称为合成矩阵。本文语音信号具有较好的稀疏性，而清音信号却不具有稀疏性。这是因为清音帧的残差信号确是一个高斯白噪声序列，如图2所示。

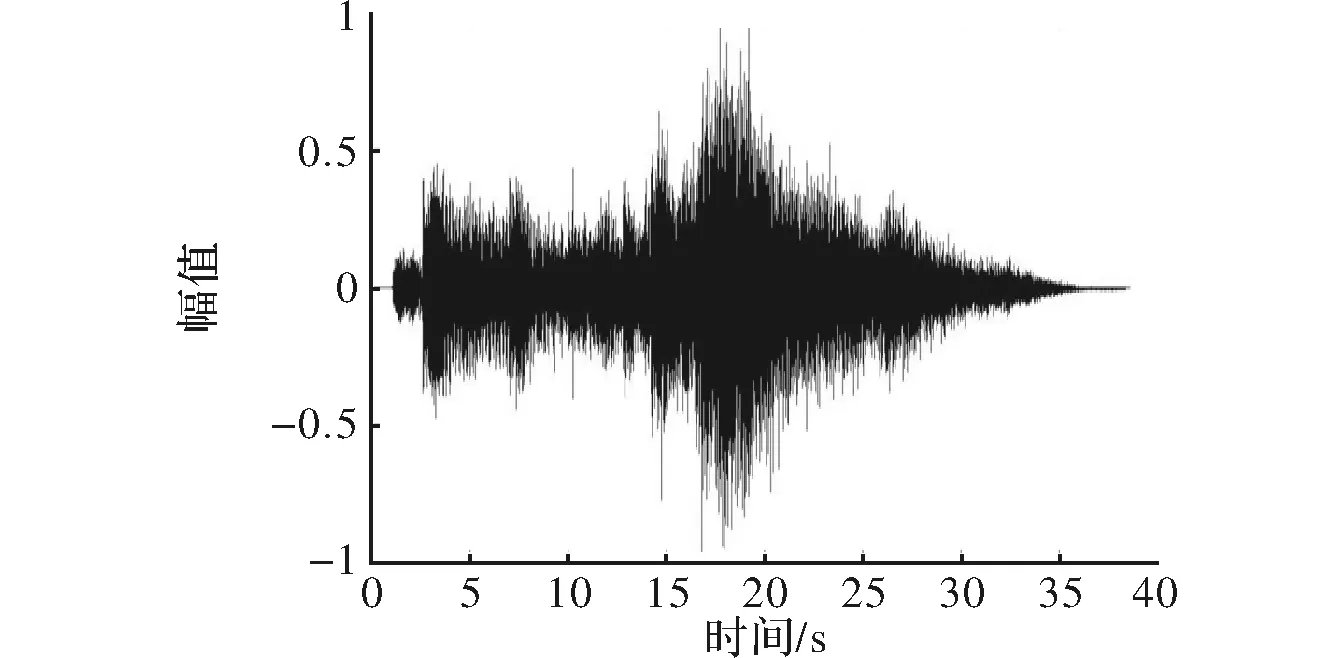
图2 一维语音信号的原始波形

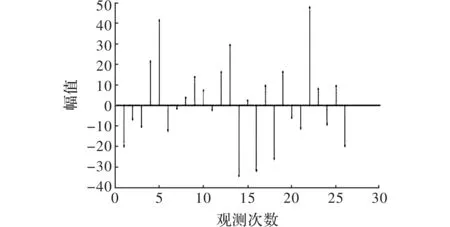
图3 原测试信号观测结果图

图3中的每帧语音是以26次观测为例。因为语音的绝大部分能量都集中在浊音部分，而清音的能量比较小，因此，清音帧的非稀疏性对语音信号在H上的压缩感知的性能的影响并不大。而基于Matlab的压缩感知算法可以进而实现原测试信号所对应稀疏信号稀疏度图，如图4所示。

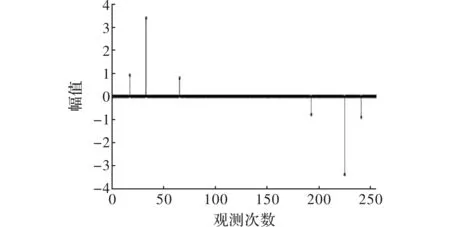
图4 对应稀疏信号稀疏度图

利用FFT稀疏化方法对语音信号局部信号(1001～1005)稀疏化表示，图5为稀疏化表示图。再基于DCT稀疏化方法对语音信号局部信号(1001～1005)稀疏化表示，得到图6稀疏化表示示意图。

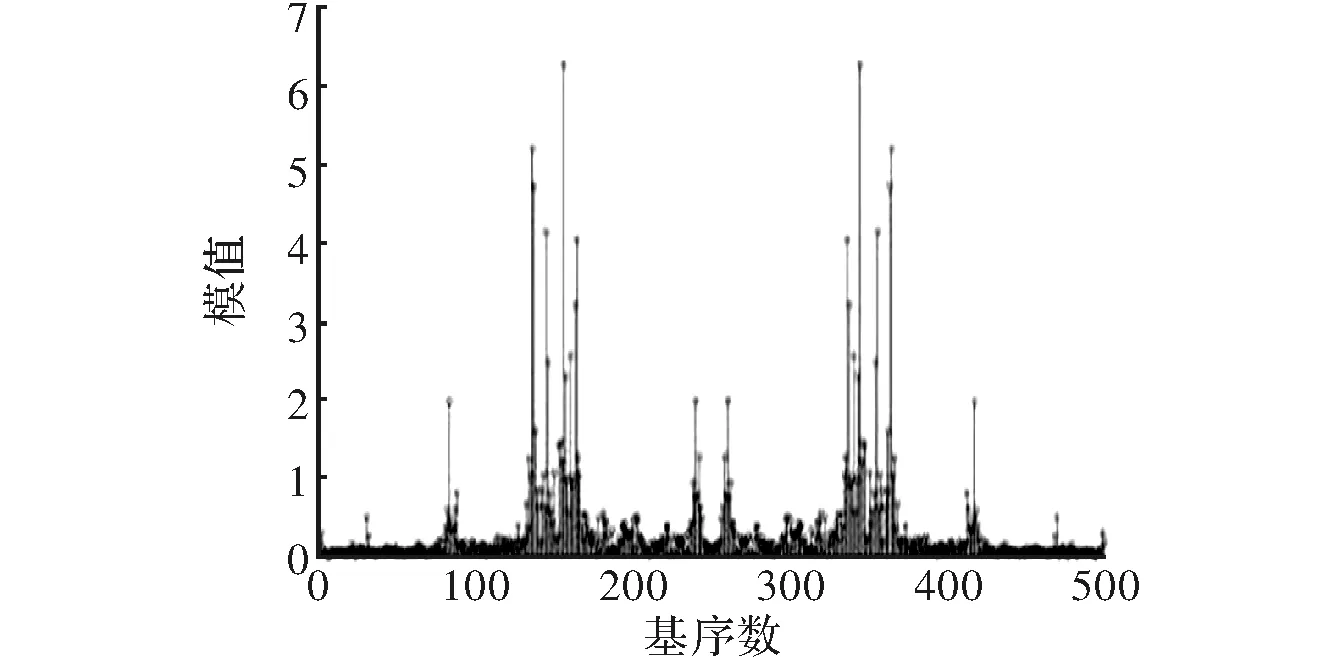
图5 FFT基对语音信号局部信号稀疏化表示图

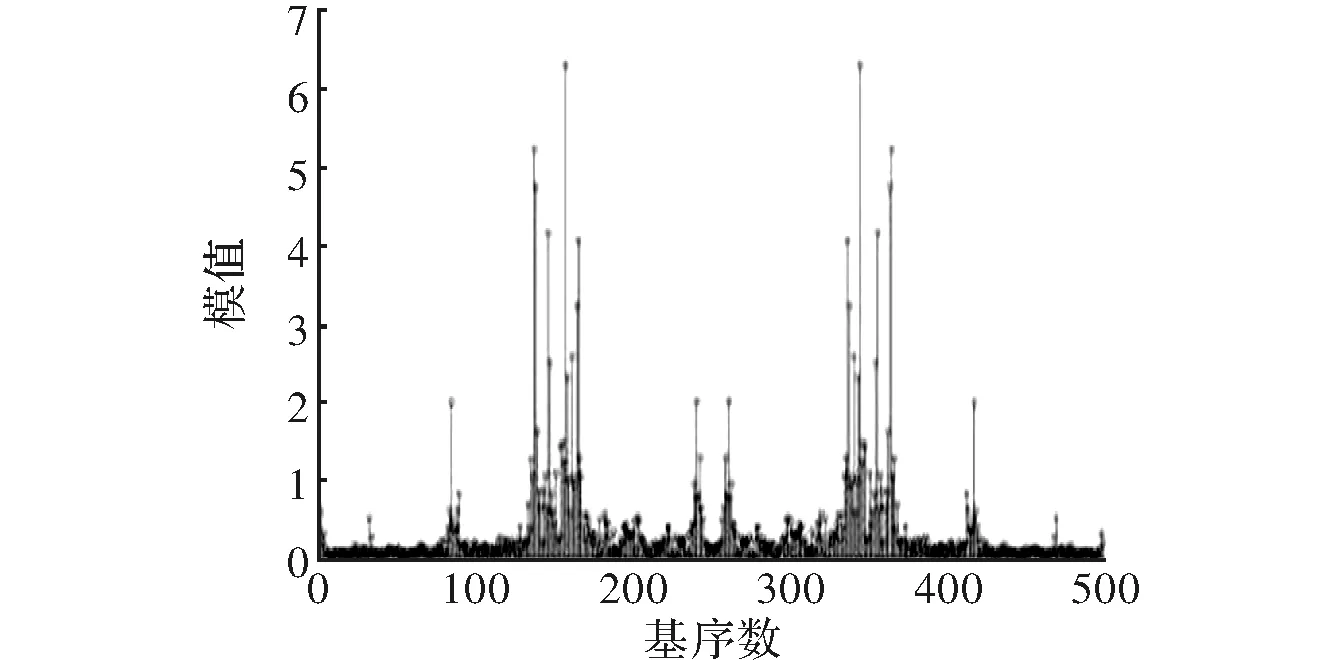
图6 DCT基对语音信号局部信号稀疏化表示图

2.2 语音信号的压缩与重构

Candes在其2006年发表的论文中证明了，只要信号是可压缩的或在某个变换域是稀疏的，就能以非常低的频率即M≪N的采样信号近乎无损地重构出原信号。基于线性预测(LP)分析的语音信号的压缩感知模型如图7所示。

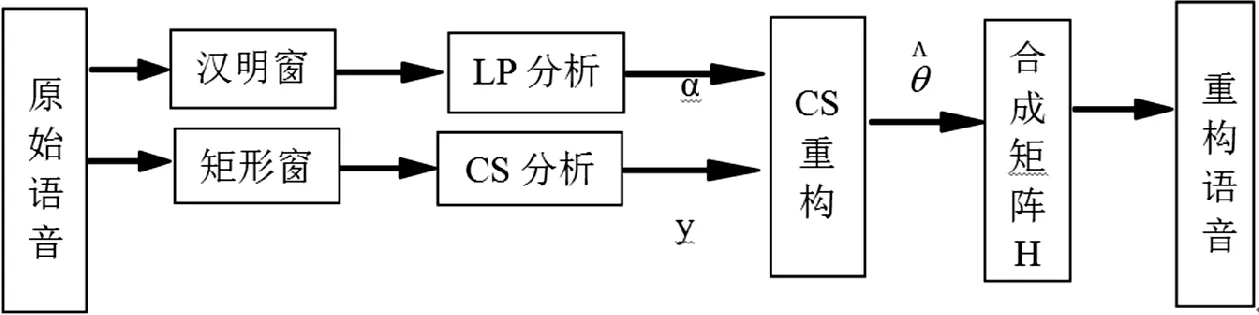
图7 算法原理

对经汉明窗和矩形窗分帧的语音信号，分别利用LP分析的技术和CS技术，提取线性预测系数向量α和观测向量y。语音信号的重构可以以线性预测系数向量α和观测向量y为已知的条件，利用解优化问题的方法来进一步实现语音信号在H域上的信号重构[9]。

语音信号压缩可以分为两个阶段：第一阶段，对语音信号进行观测，得到观测向量y；第二阶段，通过线性分析来获取每帧语音信号的p个线性的预测系数，用于构造合成矩阵H[10]。

语音信号的重构就是一个解优化问题的过程，也即通过求解L1的优化问题来进一步获得语音信号在稀疏域上的稀疏系数，利用已经合成的矩阵再将稀疏性的系数投影到语音的信号域，从而可以达到实现信号的再次重构，其原理如式(6)和式(7)所示。

(6)

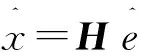
(7)

本文使用的算例对象是语音(铃声)信息，是以216次观测为例，观测矩阵Φ为M×N的随机高斯矩阵。本文主要研究语音信号在H上的CS性能和不同的变换矩阵上的重构语音信号的信噪比以及分段的信噪比，并且给出了重构语音信号的主观性上的评价。重构语音信号的质量的客观评价的方法为

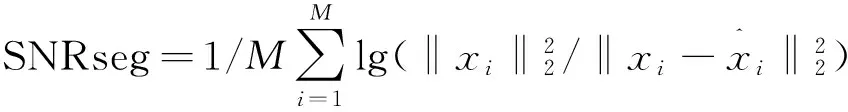
其中，M为原始语音信号的总帧数。

如图8所示，除了两端的重构语音与原始语音有一定的误差外，基本实现了语音信号的精确重构，这是为进一步获取线性预测系数，引入自相关函数时引起了误差所导致。为了能够尽可能多的去降低两端误差，在线性预测阶段使用两端具有平滑过渡特性的汉明窗[11]，在压缩感知(CS)的观测阶段使用可以确保语音信号时域特性的矩形窗。本文利用DCT基时CS恢复语音信号局部信号误差随观测次数变换图(观测次数为216次)，如图9所示。

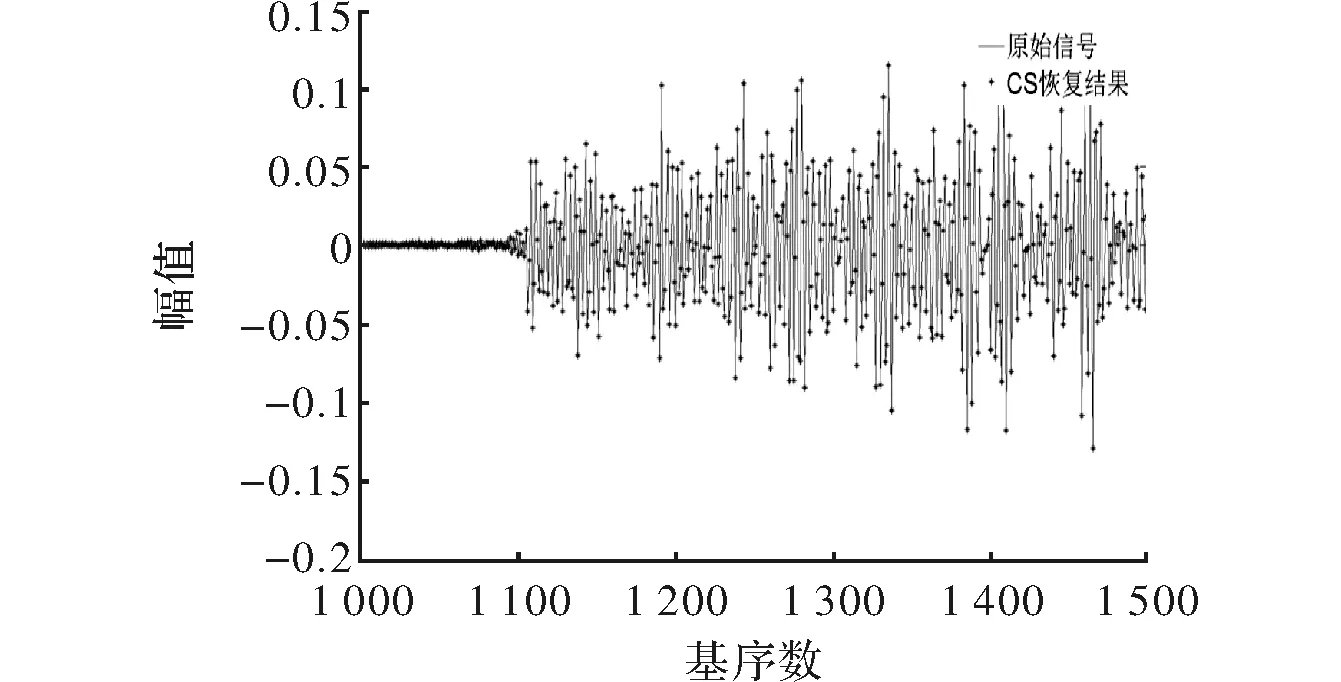
图8 利用DCT基时局部信号CS恢复结果与原信号比对图

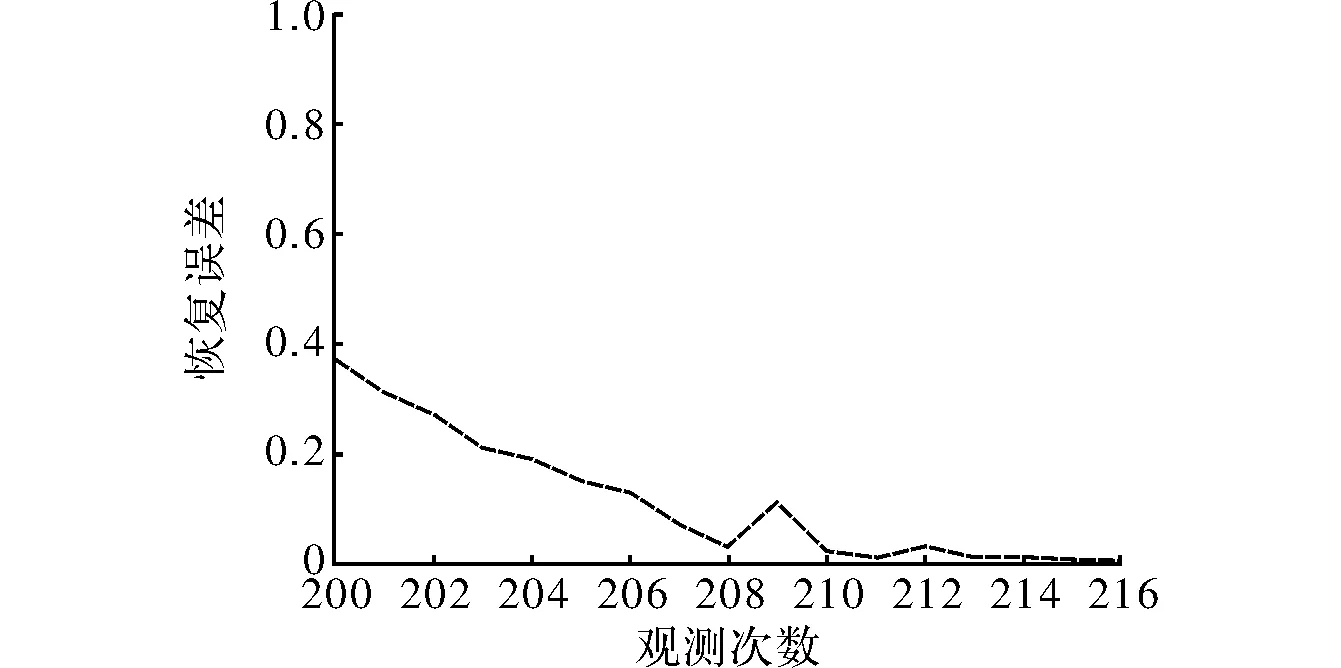
图9 利用DCT基时CS恢复语音信号局部信号误差随观测次数变换图

图9给出了语音信号在利用DCT基时CS恢复语音信号局部信号误差随观测次数变换图。从图中可以看出，语音信号在利用FFT基时CS恢复语音信号局部信号误差随观测次数变换时，随着观测次数增加，信号的恢复误差也在不断衰减，因此得到的恢复信号也更加精确；反之，得到的恢复信号会越来越差，甚至得不到恢复信号。

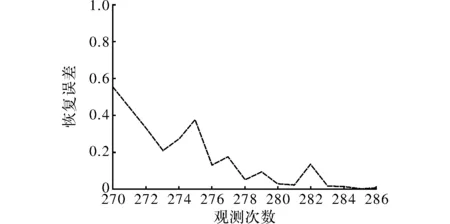
图10 利用FFT基时CS恢复语音信号局部信号误差随观测次数变换图

图10给出了利用FFT基时CS恢复语音信号局部信号误差随观测次数变换图，从图中可以看出，随着观测次数的增加，信号的恢复误差呈阶梯型递减，这表明得到的恢复信号精度越来越高。反之，得到的恢复信号会越来越差，甚至得不到恢复信号。对比图9和图10，可以得到，语音信号在利用DCT基时CS恢复语音信号局部信号误差随观测次数变换，相比于其在利用FFT基时CS恢复语音信号局部信号误差随观测次数变换更好，因为在需要达到同样恢复误差的情况下，语音信号在利用DCT基时CS恢复语音信号局部信号误差随观测次数变换所需要的感测次数，明显小于语音信号在利用FFT基时CS恢复语音信号局部信号误差随观测次数变换。经过上述处理可以进一步得到利用DCT基时语音信号局部信号CS恢复结果与原信号比对图，如图11所示。

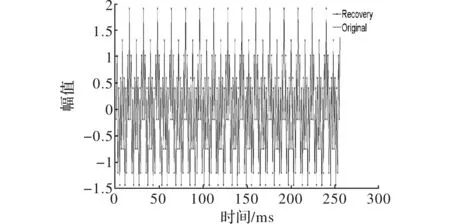
图11 恢复结果与原信号比对图

从图11可以看出，利用DCT基时的语音信号的局部恢复信号可以近乎无失真的还原出原语音信号，效果良好。

3 结束语

语音信号重构是语音信号处理的重要内容，利用正交匹配追踪算法(OMP)对语音信号重构进行设计，取得较好的效果，具有较高的应用价值，值得进一步深入研究。

[1] 李卓凡,闫敬文.压缩感知及应用[M].北京:国防工业出版社,2015.

[2] Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(2):489-509.

[3] 许小冬.基于压缩感知理论的图像重构算法研究[D].兰州:西北师范大学,2015.

[4] 沈丹丹.基于压缩感知的语音编码研究[D].南京:南京邮电大学,2012.

[5] Donoho D.Compressed Sensing[J].IEEE Transactions on Information Theory,2006,52(4):128-136.

[6] 金坚,谷源涛,梅顺良.压缩采样技术及其应用[J].电子与信息学报,2010,32(2):470-475.

[7] 马小薇.基于压缩感知的OMP图像重构算法改进[J].电子科技,2015,28(4):51-53.

[8] 石光明,刘丹华,高大化,等.压缩感知理论及其研究进展[J].电子学报,2009,37(5):1070-1081.

[9] Donoho D,Tsaig Y.Compressed sensing[J].Signal Processing,2006,86(3):533-548.

[10] Candes E.Sparsity in compressive sampling[J].Inverse Problem,2007(3):969-985.

[11] 韩纪庆,张磊,郑铁然.语音信号处理[M].北京:清华大学出版社,2004.