面向拆卸线平衡的维度学习多目标粒子群优化

肖闪丽，王宇嘉，于 慧

(上海工程技术大学 电子电气工程学院，上海 201620)

在实际生产中拆卸线平衡问题(Disassembly Line Balancing Problem, DLBP)需要同时优化多个相互牵制甚至互相矛盾的目标，是一类典型的NP组合优化问题。Gungor等人[1]首先提出了DLBP，并采用了一种启发式算法，但该方法的缺点是求解效果具有不确定性。Altekin和Llambert等人[2-3]利用启发式算法求解基于拆卸利润最优的DLBP。文献[4]提出了基于线性加权的多目标蚁群算法, 但其实质仍是单目标优化。文献[5～6]分别运用改进的蚁群算法和遗传算法求解多目标DLBP，但在实际求解过程中却把多目标问题转化成了具有优先顺序的单目标问题。Kongar等人[7]利用遗传算法，考虑了多个目标来实现DLBP，但其针对大规模问题的求解性能还有待提升。丁力平等人[8]提出Pareto蚁群算法求解拆卸线的多目标问题，其目标为平均闲置率、负荷均衡指标和拆卸成本，但在解决复杂的DLBP上可能会出现早熟现象。Kalayci等人[9-11]提出了基于邻居变异操作的粒子群优化算法、蜂群算法和蚁群算法，但其没有考虑算法自身存在易陷入局部最优的问题。

粒子群算法凭借实现容易、控制参数少以及收敛速度快的特点[12]，目前广泛应用在工业生产上。本文根据生产实际的需要构建了DLBP数学模型，并采用基于维度学习的多目标粒子群算法(DL-MOPSO)对其进行优化求解。

1 多目标拆卸线平衡问题的数学模型

1.1 拆卸线平衡问题描述

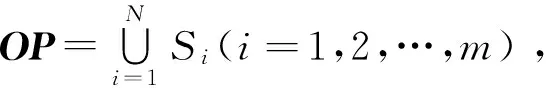
1.2 拆卸线平衡问题数学模型

(1)尽可能减小工作站的数量

minf1=m

(2)最小化工作站的空闲时间

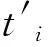
(3)最小化需求指数：根据市场需要对零件进行拆卸，减少库存压力

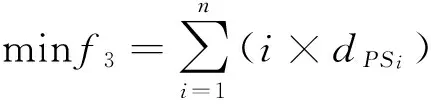
其中，PSi表示在拆卸序列中第i个零件；dPSi代表任务为PSi的零部件的需求量；N为自然数集；

(4)尽早拆除危害零部件：可减少危害，节约成本。

综上所述，本文对拆卸线平衡问题优化的数学模型如式(1)所示

minf=min{f1,f2,f3,f4}

(1)

约束条件如式(2)所示

(2-a)

(2-b)

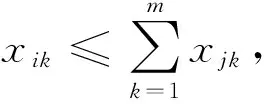
(2-c)

其中，ti为第i个任务的作业时间；式(2-a)表示每个任务必须要分配给工作站，且只能分配给一个工作站；式(2-b)表示工作站数的取值范围；m*表示所需的最小工作站数；式(2-c)表示任务i分配给工作站j时，其之前的任务都已经分配给j之前的工作站，即保证在满足拆卸任务优先关系的情况下分配作业任务；IP表示在任务i之前的集合。

2 动态邻居维度学习的多目标粒子群算法

2.1 粒子的编码与解码

拆卸线平衡问题是离散优化问题，与连续优化问题不同，在求解之前要确定粒子的编码与解码方案。本文利用带优先权的零入度拓扑排序方法建立粒子位置与拆卸序列之间的映射关系[13]。

以7个零部件的拆卸为例，其用优先图表示的拆卸任务之间的先后关系如图1所示，其拆卸优先权如表1所示。

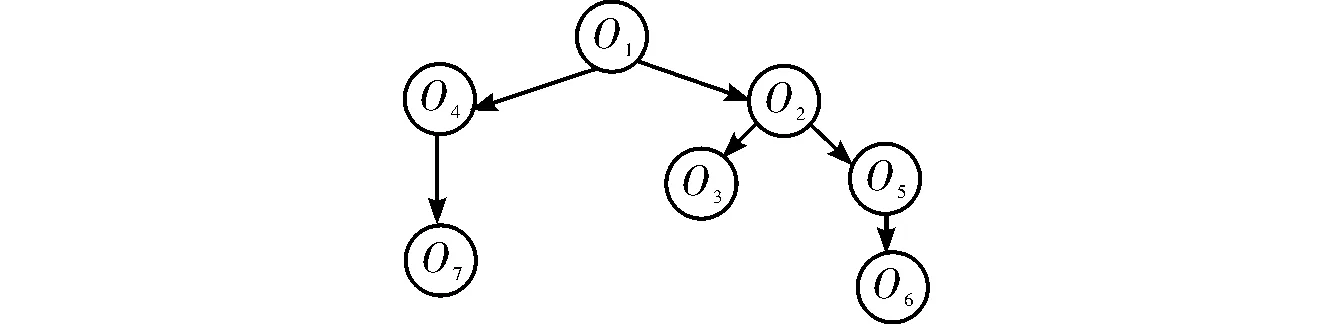
图1 7个零部件拆卸优先顺序

粒子维度1234567优先权0.20.30.40.10.50.50.6

由图1可得, 开始只有零件O1的入度为0，故选择O1为拆卸序列的第一个，接下来零件O2和O4的入度为0，但零件O2的优先权大于O4的优先权，因此下一个可用来拆卸的零件为O2。重复上述过程，直到零件集为空集。该粒子经解码后得到的可行的拆卸序列(Feasible disassembly Sequence，FOS)为[1，2，5，6，3，4，7]。

2.2 动态邻居拓扑结构

Suganthan等[14]提出了将环形结构与星形结构结合起来的动态邻居构建策略来减小种群陷入局部最优的概率。在粒子邻居数增长模型中，当任意两个粒子满足式(3)时，认定上述两粒子为邻居关系

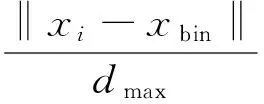
(3)

其中，xi和xbin为种群中任意两粒子；t为算法当前迭代次数；tmax为算法最大迭代次数；dmax是任意两个粒子间的最大距离。

2.3 构建最优维度粒子

为平衡学习过程中的探索性能和开发性能[15]，在DL-MOPSO算法中，选取每个粒子邻居中最优维度。

粒子i的每一维学习对象根据式(4)选取，构成的新学习个体为

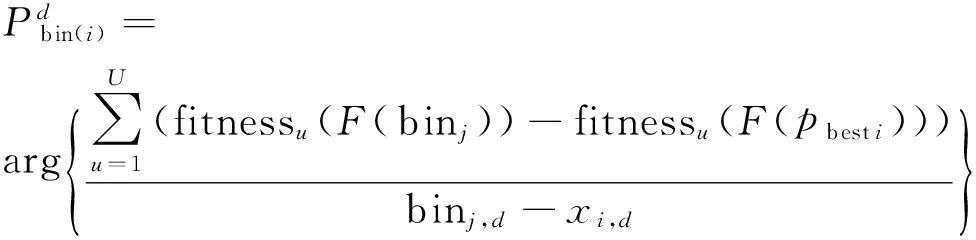
(4)

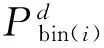
2.4 粒子的速度更新

为提高种群的多样性，本文按如下方法对粒子进行更新：

步骤 1 随机选出粒子i的p(j∈p)个维数，根据式(5-a)使粒子i向gbest学习

vi,j=wvi,j+rand()(gbestj-xi,j)

(5-a)

步骤 2 再随机选出粒子i的q(j∈q)个维数，根据式(5-b)使粒子 向邻居中最优维度组成的新个体pbestbin学习

vi,j=wvi,j+rand()(pbestbin(j)-xi,j)

(5-b)

步骤 3 剩余维数D-p-q(j∈D-p-q)根据式(5-c)使粒子i向自身的pbest学习

vi,j=wvi,j+rand()(pbesti,j-xi,j)

(5-c)

其中，p和q分别由精英概率pm和学习概率pc决定；pc决定了粒子的某一维向pbest或pbestbin的学习能力；pm决定了粒子的某一维向gbest的学习能力。

2.5 学习样本的选取和随机向导学习策略

2.5.1 全局最优位置的选取

本文根据密集距离distancei[16]的大小选择全局最优解，其计算如式(6)所示，拥有密集距离较大的粒子将作为全局最优粒子

(6)

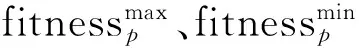
2.5.2 个体最优位置的更新

本文提出一种随机向导学习策略来更新pbest，即当一个粒子连续T代个体最优位置没有得到提升时，随机产生若干个粒子与pbest进行支配性比较，在支配的粒子中随机选择一个粒子替代pbest；当条件不满足时，随机选择一个其它粒子的pbest进行更新。

3 面向拆卸线平衡问题的多目标粒子群优化

步骤 1 算法初始化，包括：种群规模Num；外部档案规模NP；粒子位置x和速度v；搜索空间维数D(实际为拆卸产品的零件数量)；惯性权值w；粒子全局最优位置gbest；个体最优历史位置pbest；粒子最优维度个体pbestbin；学习概率pc；精英概率pm；随机向导学习持续代数阈值T；最大迭代次数tmax；目标向量f；拆卸任务偏序集Z；工作站节拍CT；

步骤 2 对粒子进行解码操作，根据优先关系确定外部档案NP中的粒子；

步骤 3 从外部档案中随机选取两个粒子，根据式(6)计算密集距离确定所对应粒子的全局最优位置gbest；

步骤 4 根据式(3)确定粒子的邻居个数，利用式(4)确定粒子每一维学习样本；

步骤 5 采用随机向导学习策略更新粒子个体最优历史位置pbest；

步骤 6 根据式(5-a)～(5-c)更新粒子的速度v；

步骤 7 计算每个FOS状态下的适应度函数，并对外部档案文件NP进行更新和维护；

步骤 8 如果终止条件成立，则停止搜索，对非劣解进行解码，输出非劣解和非劣解所对应的目标值，否则转到步骤 3；

步骤 9 对得到的最优拆卸序列完成工作站的分配。

4 实验分析

实例1 以零件数目为10的部件拆卸为例，零部件优先顺序如图2所示，其拆卸时间、需求和危害等信息见文献[17]，工作节拍CT为40s。

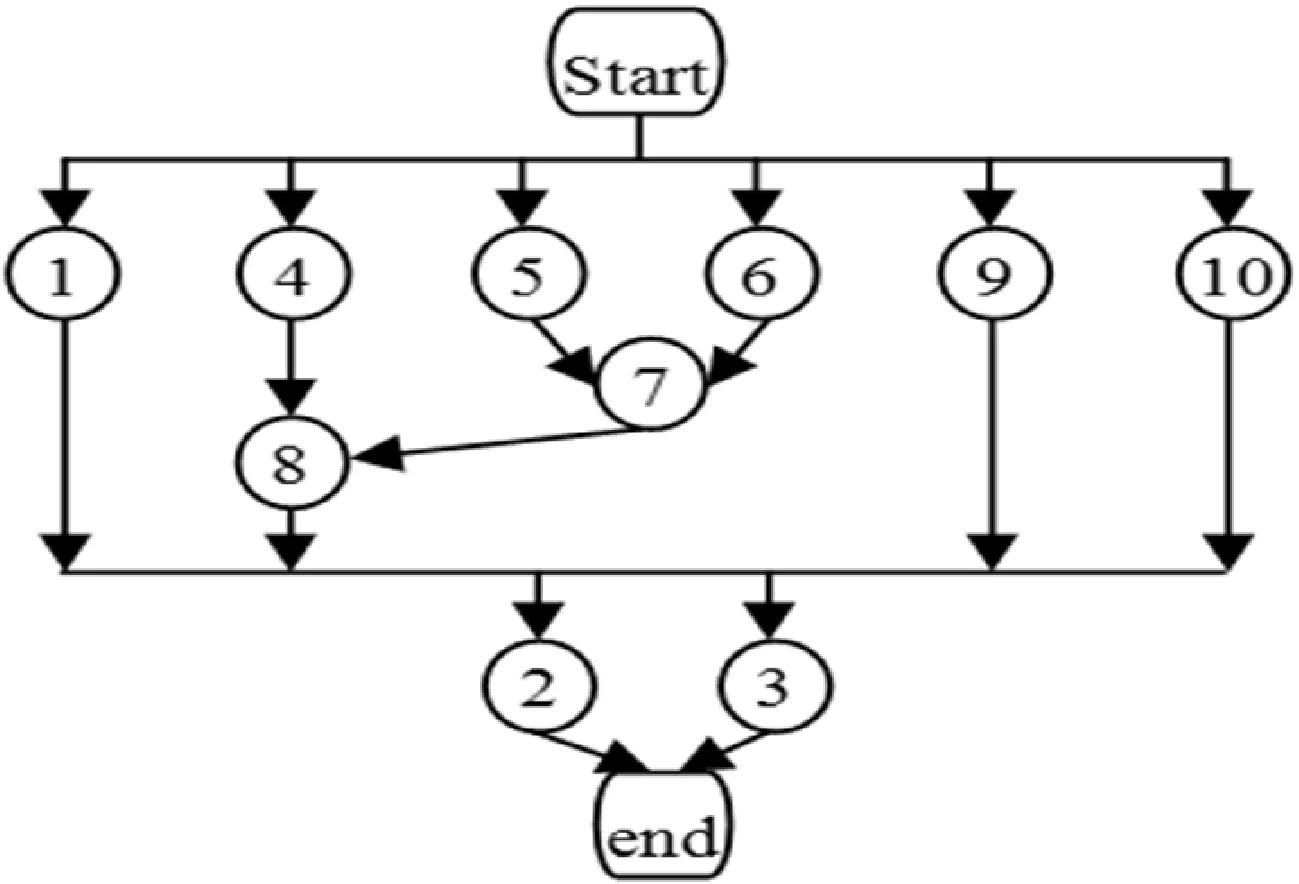
图2 零部件拆卸优先顺序

本文算法与文献[5]、文献[9]和文献[18]的优化结果进行比较，如表2所示，本文的优化结果在需求指数f3上远远优于文献[5]；相对于文献[9]和文献[18]，本文所得优化解与其互不支配。由上可得，本文所提算法的优势在于不仅得到了优于或与现有文献一致的拆卸序列，而且在考虑了生产实际情况后，为决策者提供了更多的备选拆卸方案，尤其在对产品不同需求方面为决策者提供了有利的参考。

表2 零件数目为10的优化结果

实例2 以零件数目为25的部件拆卸为例，其零部件优先顺序如图3所示，拆卸时间、需求和危害等信息见文献[19]，工作节拍CT为18s。

表3列出了现有算法在DLBP上所优化的经典解，本文所得优化解如图4所示。从表3中可以看出，文献[5]在该问题上不能得到较好结果，说明随着拆卸规模的增大，其求解精度下降。本文算法所得优化解(f1=9,f2=9,f3=806,f4=74)相比与文献[7]、文献[9]和文献[18]，在工作站数为理论值且空闲时间f2保持一致的前提下，本文算法所求得的需求指数f3和尽早拆除危害零部件f4均得到了不同程度的改善，尤其需求指数f3相对来说有了大幅度下降。根据支配解的定义，文献[18]的优化结果支配文献[7]和文献[9], 而本文得到的解在每一个目标函数上均优于文献[18]。由本实例可以看出，随着问题的复杂程度的增加，本文所提算法能够找到解决多目标DLBP较优的拆卸序列。

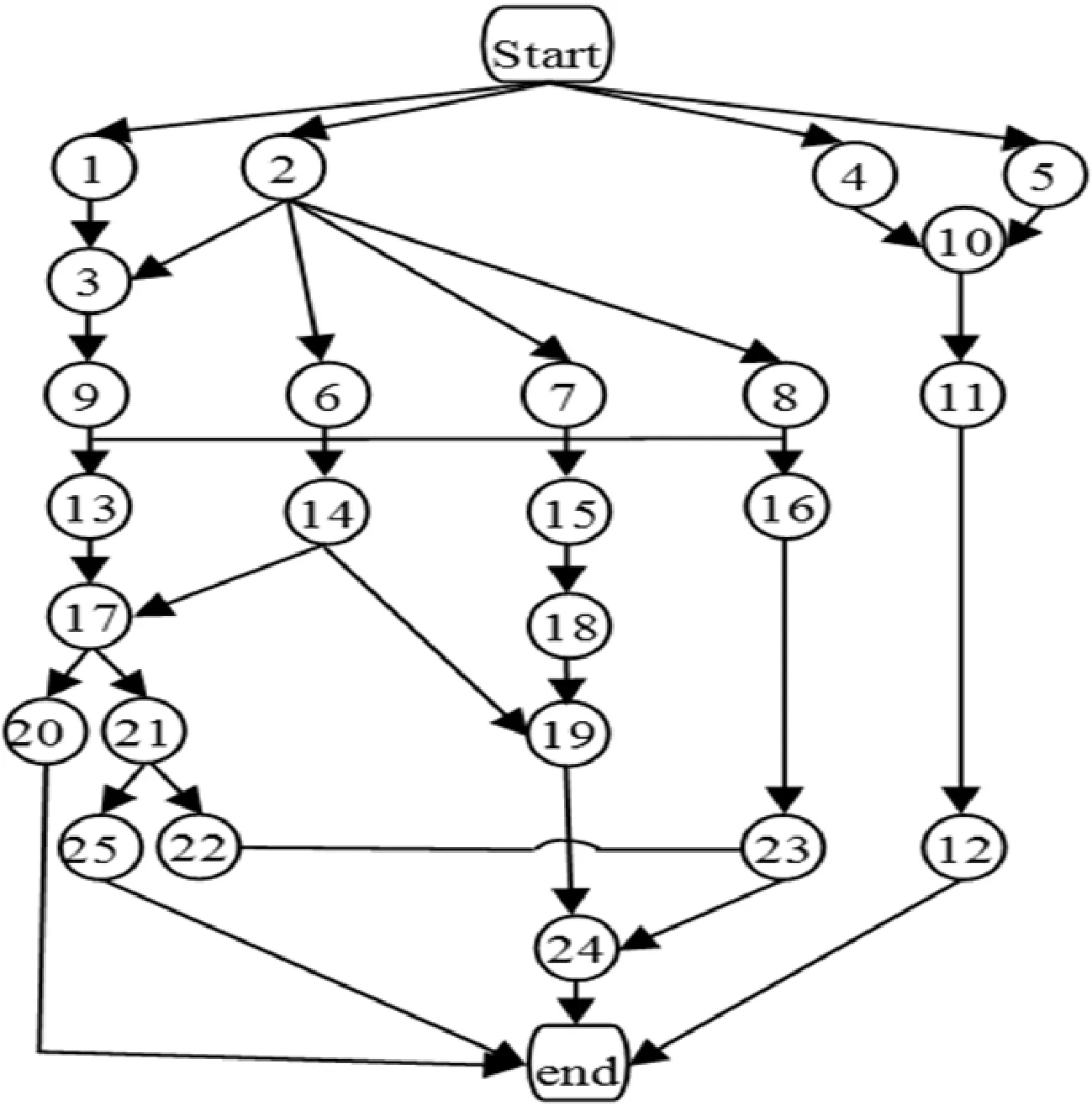
图3 25个零部件优先拆卸顺序

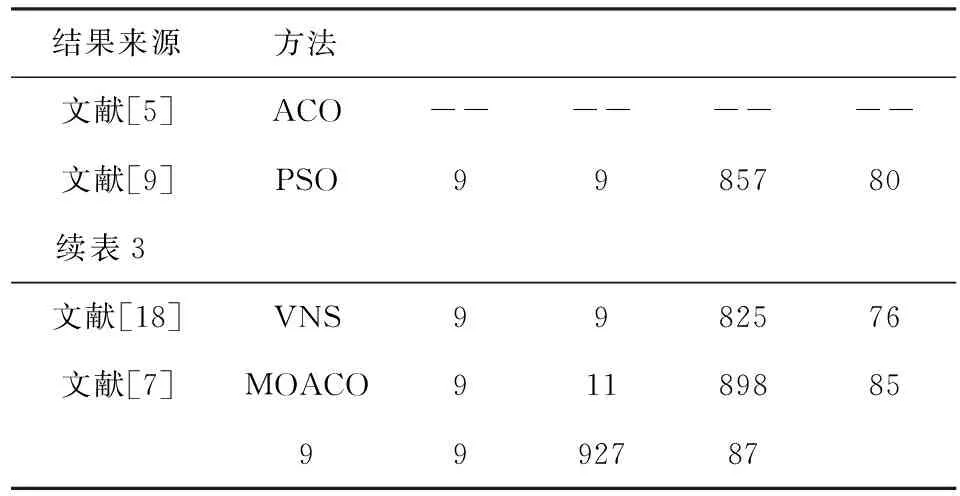
结果来源方法文献[5]ACO--------文献[9]PSO9985780续表3 文献[18]VNS9982576文献[7]MOACO911898859992787

图4 各工作站上作业元素及时间(f1=9,f2=9,f3=806,f4=74)

从上述实例可以看出，本文所提出的算法可以有效解决DLBP问题，并且随着问题规模的增大，可以显著提高拆卸效率，避免算法易陷入局部最优，在平衡多个拆卸目标的同时，给出多种拆卸策略，满足了不同决策者的实际需要。

5 结束语

本文从经济性和环保性角度，构建了包含4个决策目标的拆卸线平衡问题数学模型，并根据模型特点采用基于维度学习的多目标粒子群算法进行求解。该算法通过动态的邻居拓扑结构、最优个体维度学习和随机向导学习策略保证了种群的多样性，避免种群早熟陷入局部最优，有效提高了算法的全局搜索能力。最后，通过对不同规模的拆卸线平衡问题进行验证，结果表明本文所提出的方法在处理大规模拆卸线平衡问题时，能够为决策者提供多种拆卸策略，在满足最小工作站要求下，提高拆卸效率，为解决大规模多目标拆卸线平衡问题提供了一种有效的解决方法。

[1]GungorA,GuptaSM,PochampallyK,etal.Complicationsindisassemblylinebalancing[J].ProceedingsofSPIE-TheInternationalSocietyforOpticalEngineering, 2000, 4193:289-298.

[2]AlekinFT,KandillerL,OzdemirelNE.Disassemblylinebalancingwithlimitedsupplyandsubassemblyavailability[C].Bellingham,Washington:ProceedingsofSPIE,SPIA,2004.

[3]NazarianE,KoJ,WangH.Designofmulti-productmanufacturinglineswiththeconsiderationofproductchangedependentinter-tasktimes,reducedchangeoverandmachineflexibility[J].JournalofManufacturingSystems, 2010, 29(1):35-46.

[4]ChenBW,SongSM,ChenXL.Vehicleroutingproblemwithfuzzydemandsanditsheuristicantcolonyalgorithm[J].JournalofComputerApplications, 2006, 26(11):2639-2638.

[5]McGovernSM,GuptaSM.Antcolonyoptimizationfordisassemblysequencingwithmultipleobjectives[J].TheInternationalJournalofAdvancedManufacturingTechnology, 2006, 30(5):481-496.

[6]KongarE,GuptaSM.Disassemblysequencingusinggeneticalgorithm[J].TheInternationalJournalofAdvancedManufacturingTechnology, 2006, 30(5):497-506.

[7]DingLP,FengYX,TanJR,etal.Anewmulti-objectiveantcolonyalgorithmforsolvingthedisassemblylinebalancingproblem[J].TheInternationalJournalofAdvancedManufacturingTechnology, 2010, 48(5):761-771.

[8]KalayciCB,GuptaSM.Aparticleswarmoptimizationalgorithmwithneighborhood-basedmutationforsequence-dependentdisassemblylinebalancingproblem[J].TheInternationalJournalofAdvancedManufacturingTechnology, 2013, 69(1):197-209.

[9]BentahaML,BattaaO,DolguiA.Asampleaverageapproximationmethodfordisassemblylinebalancingproblemunderuncertainty[J].Computers&OperationsResearch, 2014, 51(3):111-122.

[10]KalayciCB,GuptaSM.Antcolonyoptimizationforsequence-dependentdisassemblylinebalancingproblem[J].JournalofManufacturingTechnologyManagement, 2013, 24(3):413-427.

[11]AwadAR,ChibanSO.Recentadvancesinglobaloptimizationforcombinatorialdiscreteproblems[J].AppliedMathematics, 2015, 6(11):1842-1856.

[12] 王闪闪.基于群智能算法的神经网路建模研究[J].电子科技,2017,30(4):56-59.

[13]DouJ,SuC,LiJ.Adiscreteparticleswarmoptimizationalgorithmforassemblylinebalancingproblemoftype1[C].ThirdInternationalConferenceonMeasuringTechnologyandMechatronicsAutomation.IEEE, 2011.

[14]SuganthanPN.Particleswarmoptimizerwithneighborhoodoperator[C].Piscataway,NJ,USA:ProceedingsofIEEECongressonEvolutionaryComputation(CEC), 1999.

[15]LynnN,SuganthanPN.Comprehensivelearningparticleswarmoptimizerwithguidancevectorselection[C].Singapore:IEEESymposiumonSwarmIntelligence, 2013.

[16]RaquelCR,NavalPC.Aneffectiveuseofcrowdingdistanceinmulti-objectiveparticleswarmoptimization[C].WashingtonDC:InGeneticandEvolutionaryComputationConference, 2005.

[17]LuC,HuangHZ,FuhJYH,etal.Amulti-objectivedisassemblyplanningapproachwithantcolonyoptimizationalgorithm[J].ProceedingsoftheInstitutionofMechanicalEngineersPartBJournalofEngineeringManufacture, 2008, 222(11):1465-1474.

[18]TrikiH,MellouliA,HachichaW,etal.Ahybridgeneticalgorithmapproachforsolvinganextensionofassemblylinebalancingproblem[J].InternationalJournalofComputerIntegratedManufacturing, 2015, 29(5):504-519.

[19]KalayciCB,PolatO,GuptaSM.Ahybridgeneticalgorithmforsequence-dependentdisassemblylinebalancingproblem[J].AnnalsofOperationsResearch, 2016, 242(2):321-354.