浅谈圆锥曲线的焦点三角形

■河南省温县第一高级中学 薛芳芳

在解析几何中,《圆锥曲线》这一章在数学学习中占很重的分量,椭圆、双曲线中有一类比较典型的问题,就是所谓的焦点三角形问题。焦点三角形的一个顶点在椭圆(或双曲线)上,其余两个顶点是该椭圆(或双曲线)的两个焦点。焦点三角形的问题往往与圆锥曲线的离心率、三角形的面积、三角形的周长和距离、角度等有关。此类问题能够较好地考查同学们对数形结合、函数与方程、转化与化归等数学思想的掌握情况。下面我们主要探讨一下有关焦点三角形与圆锥曲线的离心率方面的问题。

例1 已知F1,F2是双曲线(a＞0,b＞0)的左右焦点,以|F1F2|为直径的圆与双曲线交于不同的四点,顺次连接焦点和这四个点恰好组成一个正六边形,则该双曲线的离心率为____。

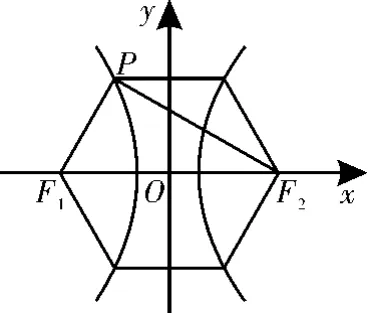
图1

解析:如图1,根据题意,易知△P F1F2为直角三角形,∠F1P F2=9 0°,∠P F2F1=3 0°,所以又|P F2|-,所以,即

点评:本题主要是利用双曲线的定义进行解题,这道题可以变化为其他题。

变式一:如图2,F1,F2是双曲线=1(a＞0,b＞0)的左右焦点,A,B是以O为圆心,|O F1|为半径的圆与该双曲线左支的两个交点,且△F2A B为等边三角形,则该双曲线的离心率为____。

图2

变式二:以椭圆的焦距为直径的圆交椭圆于四个点,这四个点连同两个焦点恰好是一个正六边形的六个顶点,则该椭圆的离心率为____。

例2 过椭圆的左焦点F作直线交椭圆于A,B两点,若|A F|∶|B F|=2∶3,且直线与长轴的夹角为,则椭圆的离心率为____。

解析:设A F=2m,B F=3m,准线为l,作A A1⊥l,B B1⊥l,垂足分别为A1,B1,过A作A D⊥B B1,交B B1于点D,由第二定义知,所以,所以,在△A D B中,所以,即

点评:本题综合考查椭圆的离心率与直线倾斜角,考查椭圆的性质和椭圆第二定义,还考查同学们的计算能力。

由例2我们可以得到一些结论:

结论3:过抛物线y2=2p x的焦点F作直线交抛物线于A,B两点,若|A F|=m,|B F|=n,直线与抛物线的对称轴的夹角为θ,则有

关于圆锥曲线的焦点三角形,本文只是谈一下自己的简单理解,希望能够对同学们的学习有所帮助,还有许多重要的性质值得我们去挖掘、研究。