巧用椭圆的几何性质解题

■河南省温县第一高级中学 闫小生

熟练掌握椭圆的几何性质,可使有关椭圆的问题轻而易举得以解决。

(2)求解与椭圆几何性质有关的问题时要结合图形进行分析,即使不画出图形,思考时也要联想到图形,当涉及顶点、焦点、长轴、短轴等椭圆的基本量时,要厘清它们之间的关系,挖掘出它们之间的内在联系。

(3)求椭圆离心率问题,应先将e用有关的一些量表示出来,再利用其中的一些关系构造出关于e的等式或不等式,从而求出e的值或范围。离心率e与a、b的关系:e2=

解析:由O,M分别为F1F2和P F1的中点,可知OM∥P F2,且,同理,ON∥P F1,且,所以四边形OMPN为平行四边形。由题意知,故即。由知,所以,故△P F1F2的周长为

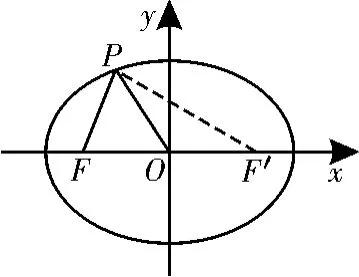
图1

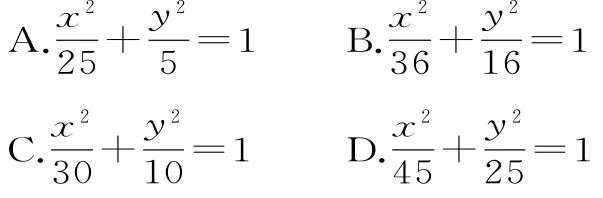
由|O P|=|O F|=|O F′|知,∠P F F′= ∠F P O,∠O F′P=∠O P F′。由∠P F F′+∠O F′P+∠F P O+∠O P F′=1 8 0°,知∠F P O+∠O P F′=9 0°,即F P⊥P F′。在R t△P F F′中,由勾股定理得,。由椭圆定义,得|P F|+|P F′|=2a=4+8=1 2,从而a=6,得a2=3 6,于是,所以椭圆C的方程为

(1)若椭圆E的焦距为1,求椭圆E的方程。

(2)设F1,F2分别是椭圆E的左右焦点,P为椭圆E上第一象限内的点,直线F2P交y轴于点Q,并且F1P⊥F1Q。证明:当a变化时,点P在某定直线上。

(2)设P(x0,y0),F1(-c,0),F2(c,0),其中由题设知x0≠c,则故直线F2P的方程为当x=0时,即点Q坐标为

(1)求椭圆C2的方程;

(2)设O为坐标原点,点A,B分别在椭圆C1和C2上,且,求直线A B的方程。

解析:(1)由已知可设椭圆C2的方程为,其离心率为,故,解得a=4,故椭圆C2的方程为

(2)设A,B两点的坐标分别为(xA,yA),(xB,yB),由及(1)知,O,A,B三点共线且点A,B不在y轴上,因此可设直线为A B的方程y=k x。

备考建议:解决直线与椭圆的综合问题时,要注意以下几点:

(1)注意观察应用题设中的每一个条件,明确确定直线、椭圆的条件。

(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力,重视根与系数之间的关系、弦长、斜率、三角形的面积等问题。

归纳总结:(1)一条规律。求椭圆标准方程的方法,除直接运用定义外,常用待定系数法(先定位,后定形,再定参)。椭圆的标准方程有两种形式,所谓“标准”,就是椭圆的中心在原点,焦点在坐标轴上。焦点F1,F2的位置决定椭圆标准方程的类型,是椭圆的定位条件;参数a,b决定椭圆的形状和大小,是椭圆的定形条件。对于方程0,n＞0),若m＞n＞0,则椭圆的焦点在x轴上;若n＞m＞0,则椭圆的焦点在y轴上。焦点位置不明确时,要注意分类讨论。

(2)两个三角形。①椭圆上的点与两个焦点构成一个三角形,该三角形称为曲线的焦点三角形,与该三角形有关的问题常常借助于正弦定理、余弦定理及比例的性质进行处理。②椭圆中有一个十分重要的△O F1B2(如图2),它的三边长分别为a、b、c。易知c2=a2-b2,若记∠O F1B2=θ,则

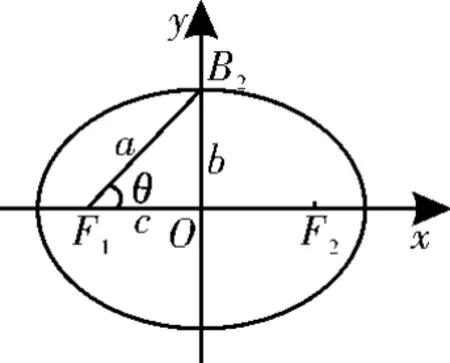
图2

(3)三个条件。椭圆方程中的a、b、c、e与坐标系无关,而焦点坐标、顶点坐标等与坐标系有关。因此确定椭圆方程需要三个条件,两个定形条件:a、b;一个定位条件:焦点坐标。