回归分析中的创新题型研究

■河南省新蔡县第一高级中学 吴文龙

概率统计中需要指出的是“离散型随机变量的概率分布”未必年年考,如2 0 1 5年全国新课标Ⅰ卷中用“可线性回归分析”替代,2 0 1 6年全国新课标Ⅲ卷中用“线性相关性检验”来代替。统计中的回归分析已是高考中的“明星”题型。笔者认为可线性回归分析与线性相关性检验特别是其创新题型应在2 0 1 8年备考中引起同学们的高度重视。

一、问题提出

从散点图中能直观地判断两个变量是否满足线性相关,当然我们利用相关系数r更能定量地计算出其线性相关的程度。当用线性关系刻画两个变量之间的关系不太好时,建议使用非线性的函数关系来描述。非线性回归的情形是两个变量之间的统计相关呈现出某种非线性关系。在这里我们不讨论一般的非线性回归,只讨论可以化为线性回归的非线性回归问题。笔者从可线性化回归分析的创新题型的实例来阐明解决这类问题的基本思想和方法。

二、创新题型展示

1.幂函数型曲线。

例1 某电视厂家准备在元旦期间举办促销活动,现根据近七年的广告费与销售量的数据确定此次广告费支出。广告费支出xi(万元)和销售量yi(万台)的数据如表1。

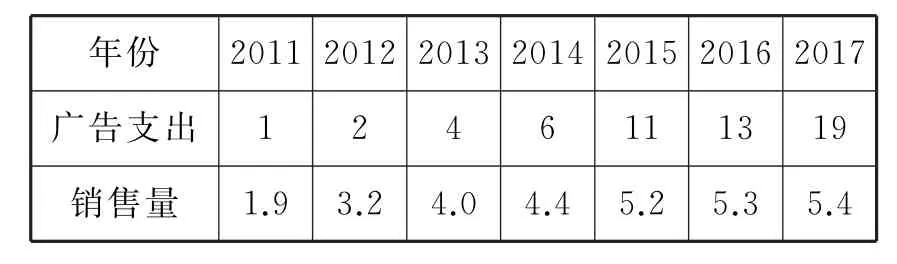
表1

(1)若用线性回归模型拟合y与x的关系,求出y关于x的线性回归方程。

(3)已知利润z与x,y的关系为z=2 0 0y-x,根据(2)的结果回答下列问题:

①广告费x=2 0时,销售量及利润的预报值是多少?

②广告费x为何值时,利润的预报值最大?(精确到0.0 1)

(2)因为0.7 5小于0.8 8且R2越大反映残差平方和越小,拟合效果越好。所以用非

故广告费为98 0 1万元时,年利润的预报值最大。

2.指数型曲线。

例2 为了研究一种昆虫的产卵数y和温度x是否有关,现收集了7组观测数据,如表2所示,两个变量并不呈线性相关关系,现分别用模型①y=C1x2+C2与模型②y=作为产卵数y和温度x的回归方程来建立两个变量之间的关系。

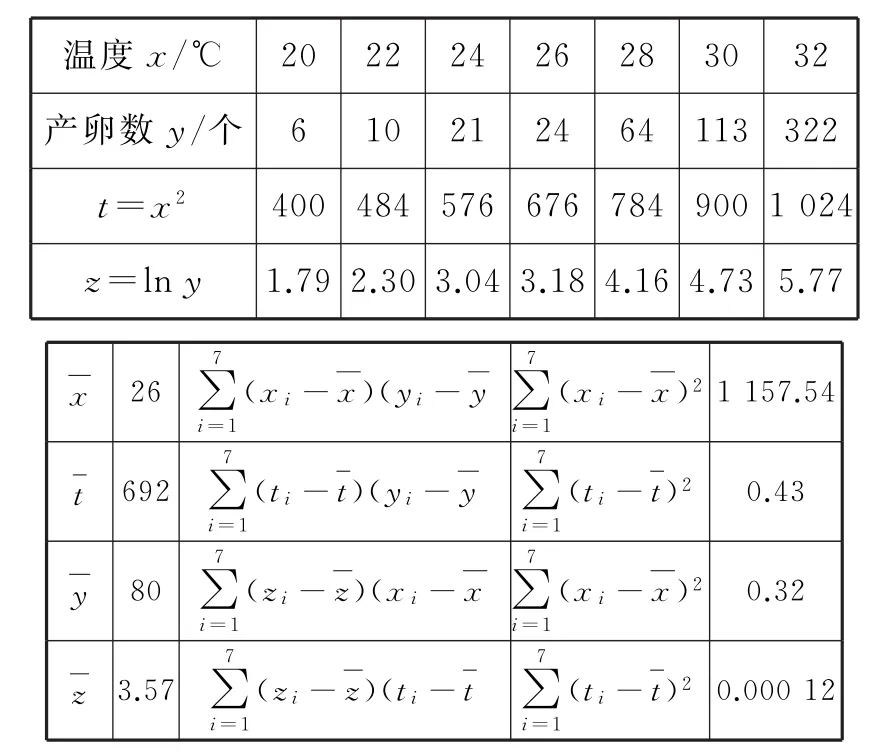
表2

附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线方程v=βu+α的斜率和截距的最小二乘估计分别为β=

(1)根据表2中的数据,分别建立两个模型下y关于x的回归方程,并在两个模型下分别估计温度为3 0℃时的产卵数。(C1,C2,C3,C4与估计值均精确到小数点后两位)(参考数据:e4.65≈1 0 4.5 8,e4.85≈1 2 7.7 4,e5.05≈1 5 6.0 2)

解析:(1)对于模型①,设t=x2,则y=C1x2+C2=C1t+C2。

对于模型②,设y=eC3x+C4,则z=l ny=C3x+C4。

点评:本题主要考查回归方程和相关指数的应用,也考查同学们的分析与判断能力,是一道综合性题目。

三、常用的将非线性回归模型转化为线性模型的技巧

对数曲线y=a+bl nx,作变换ν=l nx,得线性函数y=a+b ν。

四、抽象概括

将非线性回归问题转化为线性回归问题的步骤:

第一步,用散点图或回归分析中的相关系数r检验原始数据是不是线性相关。

第二步,若不线性相关,观察散点图,选择合适的函数进行拟合。

第三步,对选择的函数作合适的变换,从而将模型转化为线性回归模型。

最后,根据回归方程对现实中的问题进行预测。