概率统计问题易错归类剖析

■河南省新蔡县第一高级中学 田一佳

统计与概率这一模块,相对来说是同学们容易忽视的一个章节,因为必修系列的必修3讲授最快,而对于选修来说,同学们又不够重视,导致该部分的练习题虽然较易,但也容易出错。究其原因,笔者认为是本质概念未理解透彻,概念易混淆,比如:几何概型与古典概型,频率分布直方图的中位数与平均数等。笔者就这几个易错点进行简单的分析。

一、几何概型与古典概型

例1 甲、乙比赛做某道题,甲解答此题所用的时间约5～7分钟,乙解答此题所用的时间约6～8分钟。现甲、乙各解此题,求乙比甲先解答完的概率。

错解:设事件A为“乙比甲先做完此题”。由题意,甲完成此题所用时间为5、6、7分钟,三种情况。乙完成此题所用时间为6、7、8分钟,三种情况。所以,一共有3×3=9(个)基本事件。其中甲用7分钟,乙用6分钟,此事发生,除此无。所以

错因:时间在无特殊条件要求下是连续的(没有古典概型与几何概型)。

正解:设甲、乙解答本道题的时间可能为x、y分钟,则基本事件所满足的区域为

【知识补充】不同点:两个基本事件的特点不同,古典概型的基本事件有限,而几何概型的基本事件无限。

相同点:每个基本事件出现的可能性相同。

二、几何概型测量辨析

例2 如图1,在等腰直角△A B C中,∠C=9 0°,在B C上任取一点M,求∠C AM＜3 0°的概率。

旁边，一个浑身发抖的年轻男孩被人轻而易举地踢掉手中的匕首，踢倒在舞台上，一个彪悍的中年妇女捡起匕首，送进另一个人的脖子……

错解:∠C AM可以选择的可能性为0°～4 5°,记事件A为“∠C AM＜3 0°”,则

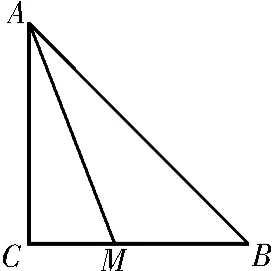
图1

错因:关键点是在B C上任取点M,所以点M可以选择的区域为B C,测度为B C的长度1。而错解却将测度记为∠C AM的度数。

正解:记“∠C AM＜3 0°”为事件A,当∠C AM=3 0°时,在R t△A CM中,A C=1,所以。因为M是从B C中任取一点,所以实验中所有可以取到的测度为1,则

【知识补充】看几何概型的测度,要找到因变量,是什么在改变,引起变化的本质是什么,那么它能所取到的所有可能为试验的总测度,满足条件时可以变动的所有可能为此事件的测度,认清本质。

三、统计图中的中位数问题

统计问题主要是以实际应用问题为载体展现,同学们需要注意的有两点:第一,弄明白题中所描述的问题,把实际问题转化为数学问题;第二,理解清楚概念,比如说频率分布直方图与频率条形图,它们的高所表示的意义不同,以及中位数、平均数、方差怎么计算,特别是中位数,不能用区间中点来表示,而是需要用到中位数的概念:最中间的数字,从而使用面积中点法去计算。

例3 海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了1 0 0个网箱,测量各网箱水产品的产量(单位:k g)。其频率分布直方图如图2和图3所示。

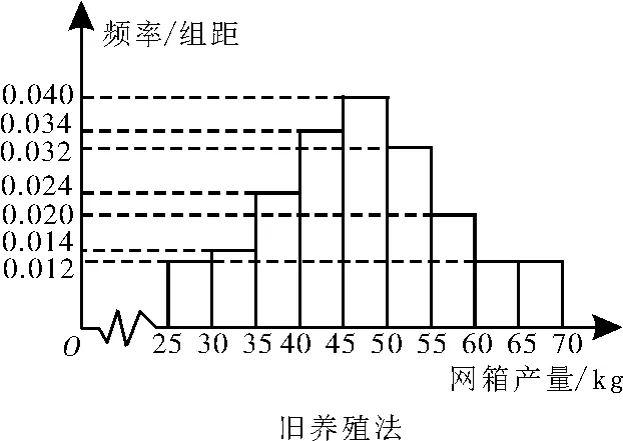
图2

(1)设两种养殖方法的网箱产量相互独立,记A表示事件“旧养殖法的网箱产量低于5 0k g,新养殖法的网箱产量不低于5 0 k g”,估计A的概率。

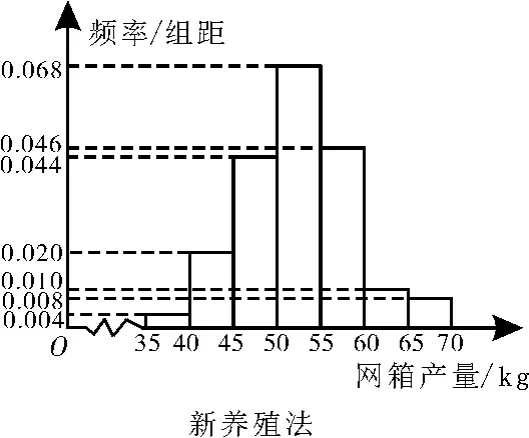
图3

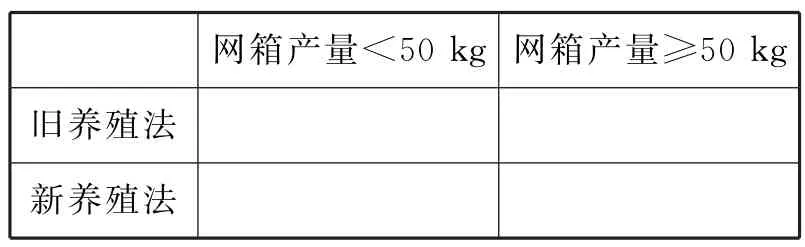
表1

(3)根据网箱产量的频率分布直方图,求新养殖法网箱产量的中位数的估计值(精确到0.0 1)。

错解:(3)由于给出的数据是频率分布直方图,所以可以用区间中点近似代替,则数据可以近似看作,2个3 7.5,1 0个4 2.5,2 2个4 7.5,3 4个5 2.5,…,所以中位数是5 2.5。

错因:在频率分布直方图中,因为没有具体的数据,只是知道数据所在区间以及所在区间的频率,所以在求解这组数据的平均数、方差时都是由区间中点去近似求解的。错解就是想当然地把中位数也类似去求解了。

正解:(1)(2)略。

(3)在新养殖法的网箱产量频率分布直方图中,网箱产量低于5 0k g的直方图面积为(0.0 0 4+0.0 2 0+0.0 4 4)×5=0.3 4＜0.5,网箱产量低于5 5k g的直方图面积为0.6 8＞0.5,故新养殖法网箱产量的中位数的估计值为

【知识补充】利用频率分布直方图求众数、中位数和平均数时,应注意三点:①最高的小长方形底边中点的横坐标即为众数;②中位数左边和右边的小长方形面积和相等,都为0.5;③平均数是频率分布直方图的“重心”,等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和。