初中数学复习的点滴做法

徐磊

【摘要】 复习是初中数学教学的一个重要环节，对于夯实学生的知识、提高数学能力有着重要的作用.复习的质量对教师的教学质量、学生的成绩有着重要的影响，复习是将学过的知识进行回顾、归纳、总结的一个过程，复习方法是否恰当直接影响着复习的效率和效果.如何提高复习的效率，也是一线教师常常探索的问题，笔者结合自身的体验，谈谈初中复习的一些做法，与同行交流.

【关键词】 初中数学;复习;做法

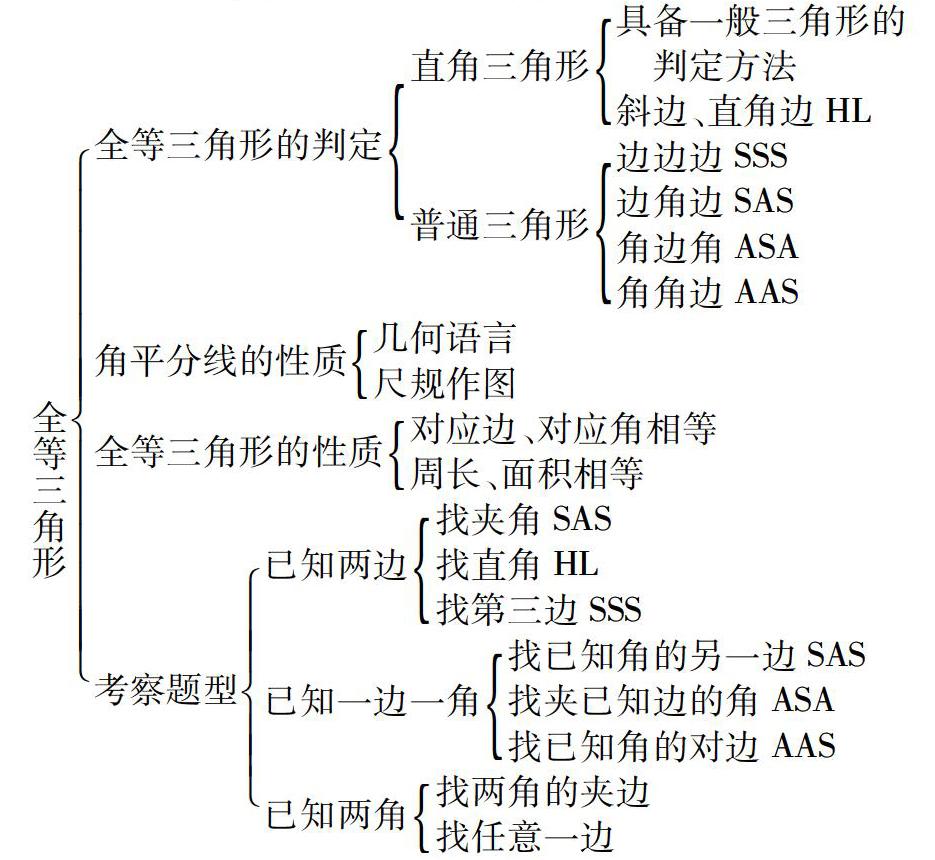
一、绘制思维导图提高复习效率

何为思维导图？思维导图又叫心智导图，是表达发散性思维的有效的图形思维工具，它简单有效，是一种革命性的思维工具.思维导图运用图文并重的技巧，把各级主题的关系用相互隶属与相关的层级图表现出来，把凌乱、枯燥的信息变成条理清晰容易理解的图形展现出来，充分运动左右大脑的机能，激发学生的创造性.

兵马未动粮草先行，在复习前我会先让学生结合教材中本章知识结构图画出本章节的思维导图.要想画出完整的思维导图，学生就要思考以下问题：本章我学习了哪些知识点？这些知识点中要注意哪些问题？哪个知识点是我掌握的？哪个知识点我还不是很理解？针对知识点会有哪些题型？教材中有哪些经典例题？教师给我补充了哪些题型？思维导图是思维的工具，它激活、整理、提升思维，在复习的过程中，学生以图形化的方式把数学知识分层整理，有利于学生更好地理解知识间的关系，在学生头脑中形成知识网络.通过绘制思维导图，学生已经初步进行了第一遍复习，待到课堂复习时学生可以结合自己的思维导图查漏补缺，既解决了存在的问题又加快了复习的节奏同时提高了复习的效率.附两张学生的思维导图供大家参考.

二、借題发挥提高复习质量

复习不同于新课学习，复习时学生已经掌握了本章节的知识，复习的过程就是把所有知识融会贯通同时进行知识、能力的提升.复习选题不在于多而在于精，所选取的题 型还应具有代表性和可开发性，所谓可开发性就是指“一题多变”“借题发挥”，将一道题目改变成多题，而题目的实质不变，让学生能根据变化找到题目之间的区别和联系，让知识点、解题方法牢牢扎根在学生脑中，培养学生思维的灵活性和解决问题的应变能力.在复习“全等三角形”这一章时我就选取了下面这道经典的题型作为复习题.

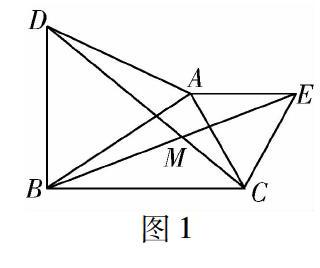
例1   已知：如图1所示，在△ABC的边BC的同侧，以AB，AC为边向外作等边三角形ABD和等边三角形ACE，连接BE、CD，相交于点M.

（1）求证：BE=CD;（2）求∠BMC的度数.

分析  （1）由等边三角形不难得出△DAC≌△BAE;

（2）△DAC≌△BAE得出∠ACD=∠AEB，再利用角之间的转化，进而可得出结论.

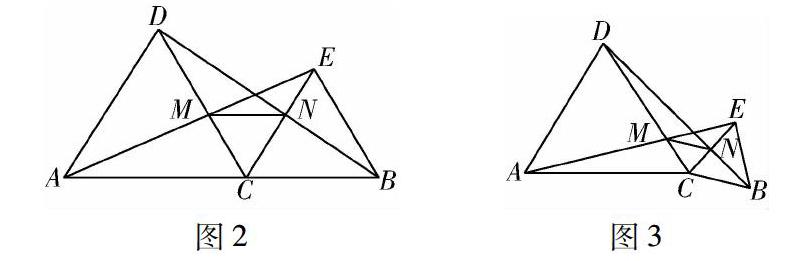
变式一  已知C是线段AB上一点，分别以AC，BC为边长在AB的同侧作等边△ADC和△CBE，连接AE和DB交于点P.

1.如图2所示，（1）证明：AE=DB;（2）求∠APB的度数.

2.如图3所示，当等边△CBE绕点C旋转后，（1）证明：AE=DB;（2）求∠APB的度数.

变式二  如图4所示，△ABC是等边三角形，分别以AB，AC为直角边，在△ABC的外侧作等腰Rt△ABD和等腰Rt△ACE，连接CD，BE交于点F.

（1）求证：CD=BE;（2）求∠DFE的度数.

变式三  如图5所示，已知△ABC，以AB，AC为边向外作正方形ABFD和正方形ACGE，连接BE，CD，求证：CD=BE.

三道变式题，虽然题目发生了变化，但是问题的本质却是不变的，主要考查了特殊三角形、正多边形的性质以及全等三角形的判定及性质，能够熟练运用其性质求解一些简单角的计算问题.通过这样复习学生更加容易通过现象看本质，举一反三，做到活学活用.

三、重视试卷分析提高复习准确率

考试是教学过程中的一个重要环节，考试的检测与反馈功能是检测是否完成教学目标的主要方式.考试主体是学生，我们经常教育学生考试是对知识的检测，考试的作用是查漏补缺.可是查哪些漏补哪些缺、怎样查怎样补是我们教师应该研究的问题，很多教师还局限在考试—批改—讲题这样的过程中，却没有进行试卷分析和总结.每一次考试不仅反映了每名学生知识、能力水平的分数，试卷中还保存着大量可以用来研究关于学生学习、教师教学情况的宝贵资料，试卷上的题目反馈出每个考生对各部分知识的掌握情况，哪些知识掌握得好，哪些知识掌握得不足，找出大多数同学得失分的共性问题.在实际教学中，我校采用筋斗云阅卷系统，网上阅卷后自动生成每一名学生的每一小题得分情况，通过小题分我可以准确地了解每名学生的知识盲点，在试卷讲评和复习时有针对性地提问学生，通过反复复习尽可能帮助学生消灭知识盲点.例如，在一次考试中我班有6名学生尺规作图0分，通过统计我得知是学号3、11、21、33、35、46这6名学生，在复习时单独检查这6名学生，课后单独进行辅导，现在全班同学都攻克尺规作图题.以下是利用筋斗云App生成的试卷小题得分表，供大家参考.

四、惜错如金、分类复习提升复习技巧

做错题目不可怕，可怕的是不知道错误的原因.学生产生错误的主要原因有：（1）概念不清;（2）审题不仔细;（3）计算错误;（4）思考不全面.平时我要求学生每周收集整理一次错题本，错题主要来源于课堂练习、课后作业、平时测试，整理错题不仅仅是把正确答案抄写一遍，而是要求学生标出错题原因、考查知识点、试题类型，把错题分门别类地进行整理，在整理错题的过程中能有效地实现知识的整合、方法的迁移.学生做错的题目我都用手机拍照记录下来，在日后的复习中反复加强训练，例如，在复习分式这一章节时，我给学生展示了一道例题.

例2   若分式方程 6 x-1 = x+5 x（x-1） 有增根，则增根是 .

很多学生看完题目毫不犹豫地填0或1，做错的本质是学生对增根的概念不理解，学生至只注意了使分式方程分母为0，但是忽略了增根是分式方程变形为整式方程的根这一要求，所以正确的答案应该是1.这道题目讲评完成我会立刻安排复习以下几个类型的题目.

1.关于x的分式方程 5 x = a x-2 有解，求字母a的取值范围是.

2.若方程 x x-1 -1= m （x+1）（x+2） 有增根，求m的值.

3.若关于x的方程 2 x-2 + x+m 2-x =2的解为整式，求m的取值范围.

通过这样分类复习，学生在短时间内掌握了一类题型，而不是东一榔头西一棒槌毫无目的性的复习，学生经历了再学习、再总结、再巩固、再提高的过程，掌握了复习的技巧，提高了学习水平.

经过近两年的探索学生感觉数学没有难学，对数学学习也更加有兴趣了，每名学生都有不同程度的进步，班级优秀率、及格率都有显著的上升，以下是我的班级近期的考试数据.

学无止境，教无定法，以上是我在教学过程中摸索的一点方法，作为一名一线教师我将继续在教育教学之路上不断钻研、探究.