巧用曲率半径解决物理问题
2018-03-04 01:04张方彦
海外文摘·艺术 2018年21期
张方彦
(南京市人民中学,江苏南京 210018)
1 题目
如图1为地球绕太阳运行的椭圆轨道,太阳位于椭圆的一个焦点上,a为近日点,b为远日点,地球在a、b两点的速度和与太阳的距离分别为V、V;R、R。求速度之比。
2 错误解法
根据万有引力定律和牛顿运动定律建立关系:

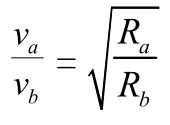
这是学生在解答过程中经常出现的错误。
3 分析
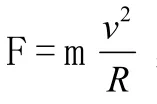
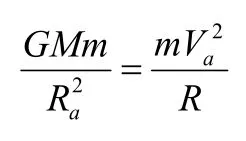
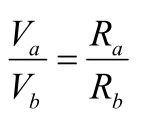
根据以前的教学的经验,学生在这个地方经常会问,上面求曲率的方法有没有理论依据?曲率半径真的是相等的吗?
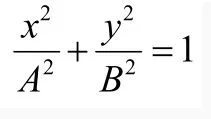
正确解法:如图3所示,太阳位于椭圆的焦点s处,太阳的质量为 M,地球的质量为m。在顶点1、2之间机械能守恒及开普勒第二定律得;

其中,c为椭圆的半焦距,即

由以上方程可求得
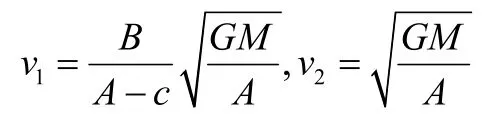
顶点1处的曲率半径ρ可有地球在该处所受的万有引力等于地球在该处的向心力求的,即

顶点2处的曲率半径ρ可由曲率圆的向心力公式求得,即

图1 地球绕太阳运行的椭圆轨道
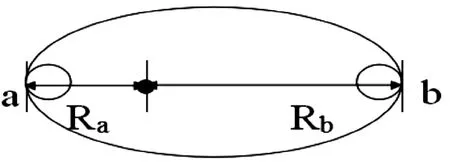
图2 在近日点和远日点作两个跟轨道相切的圆
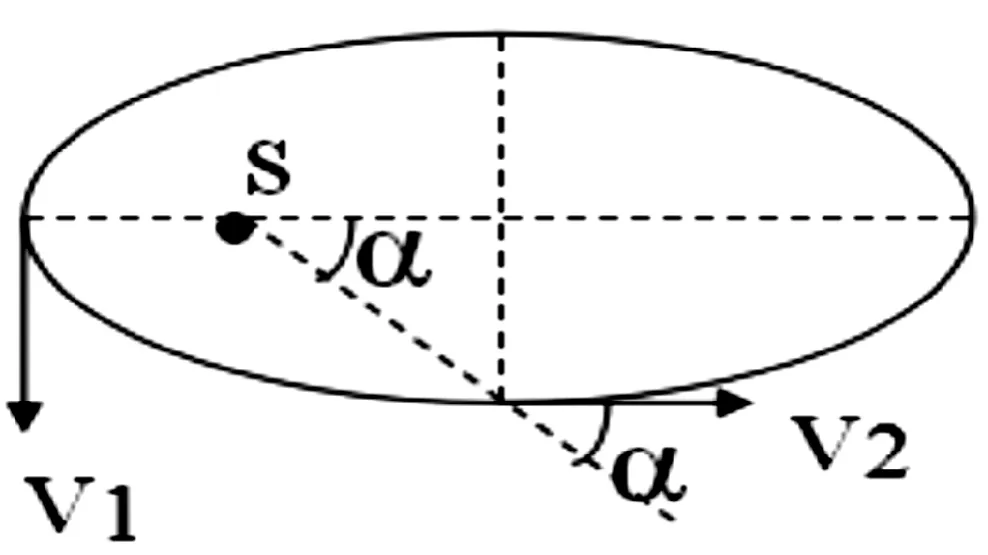
图3 太阳位于椭圆的焦点
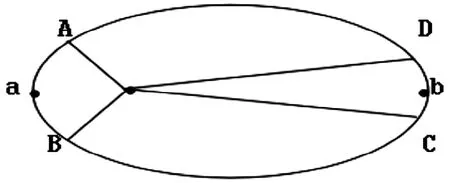
图4 两个扇形的面积图
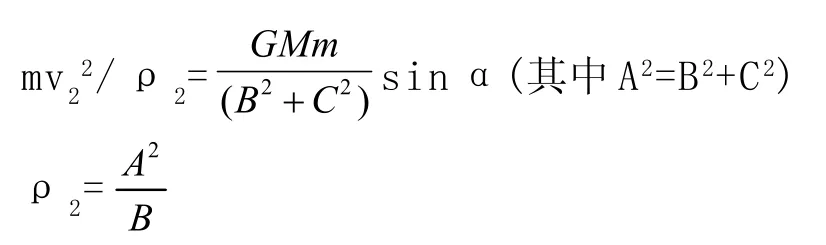
由上面的推导可以知道地球在近日点和远日点的曲率半径一定相等。
其实这个问题也可用开普勒定律来研究。根据行星运动的第三定律,行星沿椭圆轨道时,它和中心天体的连线在相等时间内扫过的面积相等,以近日点和远日点为中心,取一个极短的时间间隔Δt,在这个时间内扫过的面积如图4所示的两个扇形的面积相等。

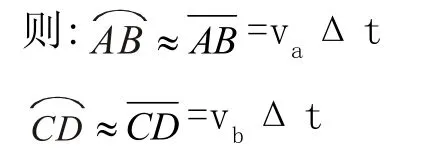
这两个扇形的面积分别为:

由于S=S可以得到

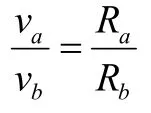

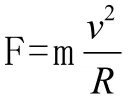
猜你喜欢
学校教育研究(2021年11期)2021-07-22
学苑创造·A版(2020年8期)2020-07-23
东方教育(2017年19期)2017-12-05
读写算·教研版(2016年19期)2017-04-17
小学生导刊(低年级)(2016年10期)2016-10-13
湖南师范大学学报·自然科学版(2016年3期)2016-06-25
初中生世界·九年级(2015年6期)2015-09-10
新高考·高二数学(2014年7期)2014-09-18
新高考·高一物理(2014年4期)2014-09-17
中学数学杂志(高中版)(2014年3期)2014-08-19

