一道抛物线高考题的解法探究及其性质推广*

广东省广州市第十六中学(510080)温伙其

解析几何是每年高考试题考查重点,很多题目切入点涉及焦点弦长问题,探索直线斜率、焦点弦长的比值及圆锥曲线离心率之间的关系.本文以一道抛物线高考试题为例,分析其不同角度的多种解法,得到两个在三种圆锥曲线都成立的性质,并从几何角度证明之,引导学生掌握知识迁移的规律,使用两个性质解决相应高考试题.

一.考题呈现

设抛物线C:y2=4x的焦点为F,直线l过F且与C交于A,B两点.若|AF|=3|BF|,则l的方程为( )

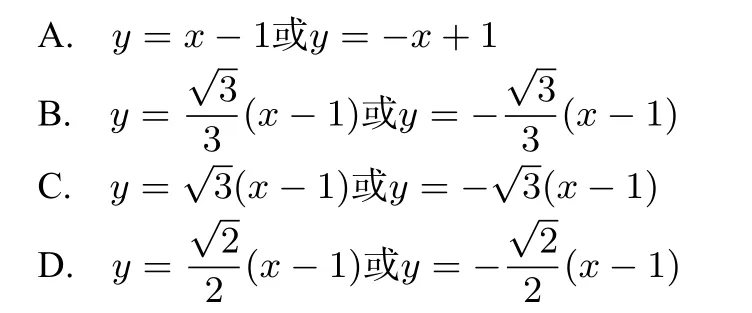
二.多种解法分析

思路一求直线l的方程,已知条件过焦点F缺斜率,而因为A,B两点为直线与抛物线的交点,所以联立直线与抛物线,得到x(y)的韦达定理,再把条件|AF|=3|BF|相应转化为x(y)的关系式,和韦达定理共同构造三元方程组,即可求kl,进而求出直线l方程.

方法1 代数法(消y)

解作图1如右所示,由题意知直线l的斜率存在,设为k,所以直线l方程为y=k(x-1)由得k2x2-2(k2+2)x+k2=0.设A(x1,y1),B(x2,y2),所以

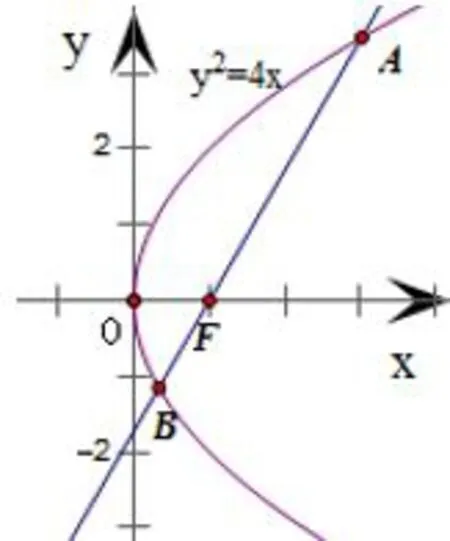
图1

方法2 代数法(消x),解答过程同上.

思路二此题的关键点在于求出直线的斜率,解题时可以尝试构造倾斜角所在特殊三角形,通过特殊几何图形求斜率.作出图二,则倾斜角θ为∠AFx,而∠AFx=∠FAM,所以在Rt△BQA中可求出直线l斜率k=tanθ=tan∠BAQ.

方法3 几何法

解作图2如右所示,令|BF|=t,则|AF|=3t.过点A作AM⊥准线,垂足为M,则|AM|=|AF|=3t.过点B作BN⊥准线,垂足为N,则|BN|=|BF|=t.

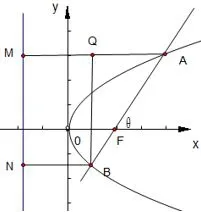
图2

在Rt△BQA中,因为|AQ|=|AM|-|BN|=2t,所以|BQ|2=|AB|2-|AQ|2=(4t)2-(2t)2=12t2,所以所以直线l的斜率为故选C.

方法4 几何法

解作图3如右所示,令|BF|=t,则|AF|=3t.令直线AB交抛物线准线于点R,过点A作AM⊥准线,垂足为M,则|AM|=|AF|=3t.过点B作BN⊥准线,垂足为N,则|BN|=|BF|=t.因为Rt△RNB～Rt△RMA,后面过程类似方法3.

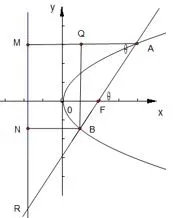
图3

思路三直线l过抛物线的焦点F和抛物线交于A,B两点,所以|AF|,|BF|都为抛物线的焦半径,令直线l的倾斜角为θ,则有结合条件|AF|=3|BF|即可求出斜率.

方法5 焦半径法

解因为直线l过抛物线的焦点F交抛物线于A,B两点.令直线l的倾斜角为θ,则有

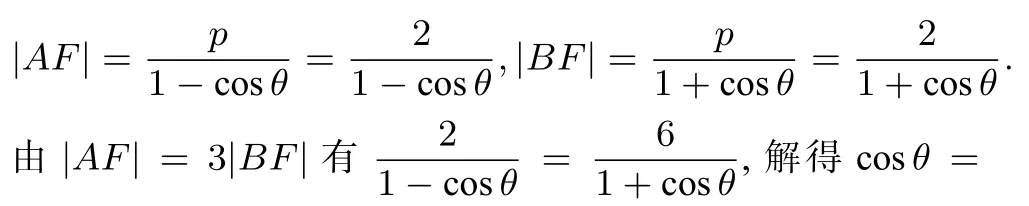
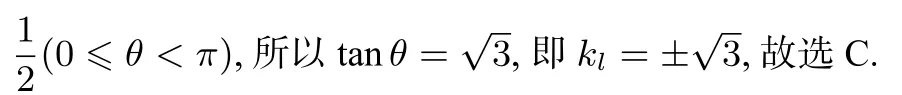
思路四直线l过抛物线的焦点F,则可把直线l表示为倾斜角θ的参数方程,联立直线与抛物线,得到参数t1,t2的韦达定理,结合条件|AF|=3|BF|可构造t1,t2,θ的三元方程组,可求出sinθ(cosθ),从而得到斜率.

方法6 直线参数方程法

三.得出两个性质

抛物线的焦点弦长具有以上图形性质,类比推理到椭圆与双曲线,也有类似的图形性质.更一般地,直线斜率、两段焦点弦长比值和圆锥曲线离心率三者间具有特定的关系结构,本文简称为圆锥曲线焦点弦长比特征公式,他们的关系如下:

以椭圆为例证明性质1.

当椭圆的焦点在x轴时,作图如图4所示.设直线l过椭圆的左焦点F1,令|BF1|=t,则|AF1|=mt.过点A作AM⊥左准线,垂足为M,过点B作BN⊥左准线,垂足为N,由椭圆第二定义有在Rt△BQA中,因为所以

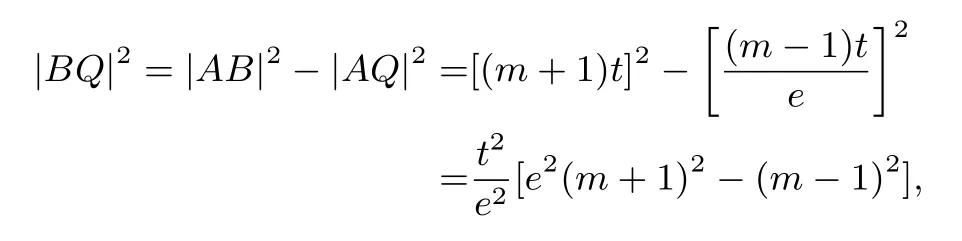
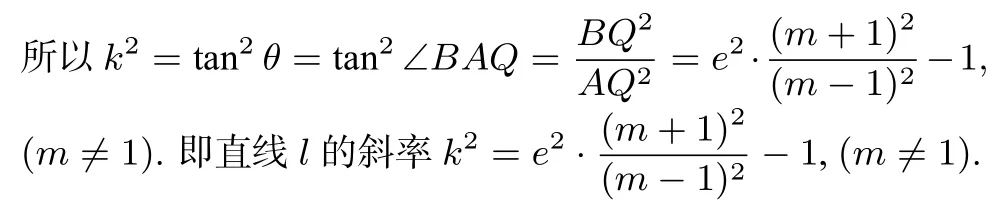
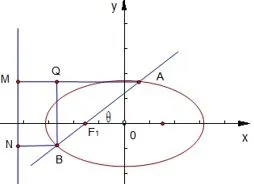
图4

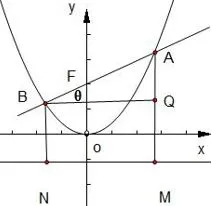
图5

以抛物线为例证明性质2.

当抛物线的焦点在y轴时,作图如图5所示.令|BF|=t,则|AF|=mt.过点A作AM⊥准线,垂足为M,过点B作BN⊥准线,垂足为N,过点B作BQ⊥AM,垂足为Q,由抛物线定义有|BN|=t,|AM|=mt.

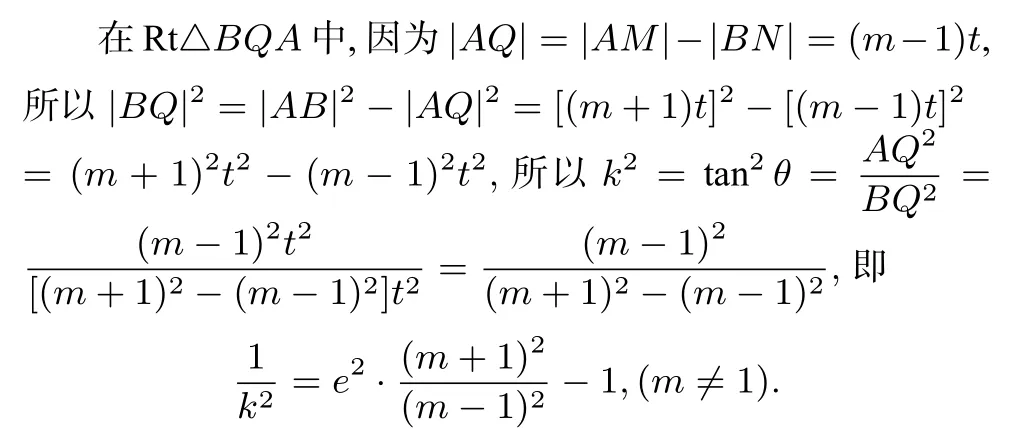
四.两个性质在近年全国高考题中的应用

例1 (2013年新课标II卷文科第10题)本文的引例.

例2 (2014年新课标II卷文科第10题)设F为抛物线C:y2=3x的焦点,过F且倾斜角为30°的直线交于C于A,B两点,则|AB|=( )

上述四道高考题,用本文得到的圆锥曲线焦点弦长比特征公式,都能快速解决！此处从略.