浅谈多面体外接球半径的求法

广东省深圳市罗湖区翠园中学(518003)吴漫华

近年来,求多面体的外接球半径成为全国各地高考的热点问题,是考察学生空间想象能力、画图能力和分析问题能力的一类综合题型,难度中等偏上.这类问题也是学生失分的重灾区,主要存在以下难点:一不能选择恰当的角度认识多面体;二不能准确分析几何体的线面关系找到球心.这两个困难让学生对此类问题无从下手,渐渐地对此类问题失去信心.本文从“画法”到“算法”,简单归纳出几类多面体的外接球半径的典型求法,试图突破此类问题在高三复习中的教学难点.

一、通过补形直接求半径

若多面体的每个顶点都落在长方体(或直三棱柱)的顶点上,那么该多面体的外接球也是该长方体(或直三棱柱)的外接球.直三棱柱的外接球球心是上下底面外心连线的中点.已知直三棱柱ABC-A1B1C1,设其上下底面√的外接圆半径为r,三棱柱的高为h,则其外接球半径长方体的外接球球心是体对角线的中点.设长方体的长宽高分别为a,b,c,则其外接球半径

(一)墙角锥

若在一个三棱锥中,共顶点的三条棱两两垂直,那么我们可以把它补形成一个长方体.

例1 三棱锥P-ABC的三条侧棱两两垂直,三_个侧面的面积分别是则该三棱锥的外接球的体积是( )

图1

(二)三对对棱分别相等的四面体

若一个三棱锥的三对对棱分别相等,那么我们可以把这个三棱锥看成是由一个长方体的六个面对角线构成的.

例2 在三棱锥A-BCD中,则三棱锥A-BCD外接球的半径为___.

分析如图2,易得a=1,b=1,c=2,所以

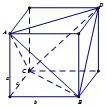
图2

(三)四个面都是直角三角形的三棱锥

利用长方体的线面关系,可将四个面都是直角三角形的三棱锥放在长方体内.

例3 (2017届广州一模,10)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑．若三棱锥P-ABC为鳖臑,PA⊥平面ABC,PA=AB=2,AC=4,三棱锥P-ABC的四个顶点都在球O的球面上,则球O的表面积为( )

图3

A.8πB.12πC.20πD.24π

分析如图3,三棱锥P-ABC四个面都是直角三角形.因为PA=AB=2,所以所以

(四)可补形成直三棱柱的四棱锥

例4 某几何体的三视图如图4-1所示,则该几何体的外接球的表面积为___.

图4-1

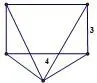
图4-2

图4-3

分析由三视图还原几何体如图4-2所示,把该四面体补成一个直三棱柱,如图4-3.底面ABC的外接圆半径r=2,所以

二、画球找球心求半径

若题目给出的多面体无法通过“补形”构造出相应的三棱柱或四棱柱等特殊几何体,那么应当选择合适的角度画出该多面体的外接球,从而找出球心求半径.

要画好多面体的外接球,通常先画球,再根据多面体的性质把多面体放入球内.如何画好球?先画球的两个互相垂直的截面⊙O和⊙O′(如图5),其中点A、点B是两个截面圆的公共点.由面面垂直的性质可知,OO′⊥⊙O′.要求外接球半径R,只需求出底面外接圆半径r,和球心到底面的距离d即可(如图6),其中

图5

图6

图7

(一)多面体中有一条侧棱垂直于底面

若多面体有一条侧棱垂直于底面,设为PA,因为⊙O⊥⊙O′,AB是这两个垂面的交线,所以由面面垂直的性质定理可得,P点一定落在大圆上.在大圆⊙O中,PA⊥PB,因为∠PAB=90°,所以连接PB一定经过圆心O,如图7,所以

例5 一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为底面周长为3,则这个球的体积为____.

图8

例6 若三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面AB=1,AC=2,∠BAC=120°,则球O的表面积为____.

图9

(二)多面体的高经过球心

如图10所示,若多面体的高经过球心,则多面体的顶点落在大圆上,如图P点.设多面体的高为H,底面ABC在小圆⊙O′上,其外接圆半径为r,所以PO=R,d=OO′=PO′-PO=H-R,列方程R2=(H-R)2+r2,即可求出外接球半径R.

图10

例7 在正三棱锥P-ABC中,侧棱PA与底面ABC所成的角为60°,则该三棱锥外接球的体积为( )

图11

三、利用球心定义求半径

多面体的每个顶点都落在其外接球的球面上,所以球心O到每个顶点的距离相等.若能找出到多面体各顶点距离相等的点,即可确定球心.

(一)有两个共斜边的直角三角形形成的四面体

若四面体中有两个有公共斜边的直角三角形,根据直角三角形中,斜边的中线等于斜边的一半可知BO=DO=AO,BO=DO=CO,所以点O到四面体的每个顶点距离都相等,则O是其外接球球心.此方法也可解决前面例3.

图12

例8 在三棱锥S-ABC中,SB⊥BC,SA⊥AC,SA=AC,SB=BC,AB边长是SC一半,且_三棱锥S-ABC的体积为则该三棱锥的外接球半径为( )

图13

A.1B.2C.3D.4

分析因为SB⊥BC,SA⊥AC,所以SC是Rt△SCA和Rt△SCB的斜边,所以球心O在SC中点上.又因为SA=AC,SB=BC,所以SC⊥AO,SC⊥BO,所以SC⊥平面ABO.如图13因为OA=OB=R,所以△OAB是等边三角形,所以所以R=3.

(二)通过面的外心垂线找球心四面体中任意两个面过其外心的垂线的交点既是球心.△ACD的外心是O1,△ABC的外心是O2,分别过O1,O2作该面的垂线,则垂线OO1,OO2上的点到△ACD,△ABC的三个顶点距离相等,所以OA=OB=OC=OD,则O为球心.

例9 (2017年太原一模)如图14,平面四边形ABCD中,BD⊥CD,将其沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,若四面体A′BCD的顶点在同一个球面上,则该球的表面积为( )

图14

分析如图15所示,底面BCD为Rt△,其外心为BC中点E,过E作垂线t.又侧面BDA′也为Rt△,其外心为BD中点F,过F作该面的垂线u,则u与t的交点E为其外接球球心,易得该外接球表面积S=3π.

图15

例10 (2017年太原二模)已知三棱锥A-BCD中,AB=AC=BC=2,BD=CD=点E是BC中点,点A在面BCD的射影恰好在DE的中点,则该三棱锥外接球表面积为____.

图16

分析如图16,因为所以∠BDC=90°,所以△BCD的外心是BC中点E,过E作△BCD的垂线n.因为△ABC是等边三角形,所以外心是中线AE的三等分点F,过F作△ABC的垂线m,所以m,n的交点O即为外接球球心.易得△OEF～△EAH,所以其中所以所以

例11 (2017高考全国1卷文科第16题)已知三棱锥S-ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S-ABC的体积为9,则球O的表面积为____.

图17

分析如图17,SC是球的直径,则SA⊥AC,SB⊥BC.且平面SCA⊥平面SCB,SA=AC,SB=BC,所以OB⊥OA,OS⊥OB,OA⊥OS,所以所以R=3,所以S=36π.

(三)建立空间直角坐标系求半径

例12 已知三棱锥A-BCD中,AD=BD=CD=2,∠BDA=∠CDA=120°,面ABD⊥面ACD,则三棱锥A-BCD的外接球表面积为____.

图18

图19

分析因为面ABD⊥面ACD,∠BDA=∠CDA=120°,以D为原点建立空间直角坐标系.如图18,易得D(0,0,0),A(2,0,0),设球心O(x,y,z),由球心性质知OA=OB=OC=OD,由两点距离公式得:x2+y2+z2=(x-2)2+y2+z2,所以R2=|OD|2=x2+y2+z2=7,所以S=28π.