基于旋转三角形模型的负泊松比蜂窝材料面内动态压溃行为数值模拟

卢子兴， 武文博

(北京航空航天大学 固体力学研究所, 北京 100083)

0 引言

负泊松比多孔材料是一种典型的拉胀材料，因其具有优异的抗剪切性能、抗压痕性和更高的能量吸收性能以及同向曲率特性等[1]，故在航空航天[2]、汽车工业[3]、人体防护等领域有着广泛的应用前景。因此，近年来关于负泊松比多孔材料力学模型的研究和动态力学行为的研究已经成为该领域的热点研究内容。文献[4]介绍了拉胀泡沫材料的力学性能，并指出：导致负泊松比效应产生的机制主要是内凹机制与旋转机制。文献[5]指出在动态冲击下，负泊松比行为的产生机制与静态加载下一致，均为内凹和旋转。对于二维多孔拉胀材料而言，基于这两种机制的构型主要有内凹六边型[1]、双箭头型[6]以及手性结构[7]等。关于具有负泊松比效应的新构型研究，文献[8]提出了一种基于旋转机制的二维多胞材料力学模型，并指出通过调整该力学模型胞壁长度的比值以及特征角可以改变该力学模型的刚度系数，甚至呈现“负刚度”的特征；文献[9]对内凹六边型模型进行改进，得到了一种具有更高弹性模量的负泊松比构型，并通过理论分析与数值模拟的方法对其弹性性能进行了研究。此外，针对二维拉胀力学模型研究，旋转三角形、旋转矩形以及十字手性等能导致负泊松比效应的构型也受到了广泛关注[10]。例如， Grima等[11]基于旋转机制分析了弹性铰接刚性三角形的构型变化，导出该系统可产生不变的正轴泊松比(-1)，而利用能量原理可导出该系统两个正轴弹性模量相等，且由构型的几何参数和铰点的刚度确定。关于不同构型负泊松比蜂窝材料的动态压溃行为，目前也已有不少学者进行了数值模拟研究。例如，张新春等[12]研究了胞元扩张角对内凹六边形蜂窝材料动态压溃行为的影响。卢子兴等[13]通过数值模拟的方法，对四边手性蜂窝材料的动态压溃行为进行了研究，分析了其变形模式以及能量吸收性能等，并与正六边形蜂窝的动力学性能进行了对比。Qiao等[14-15]对双箭头型蜂窝材料的面内冲击力学行为进行了系统研究，通过理论与数值模拟的方法研究了均匀双箭头型蜂窝材料以及功能梯度型蜂窝的平台应力、能量吸收等力学性能。此外，Liu等[16]研究了梯度设计以及不规则性对内凹六边形蜂窝冲击动力学行为的影响，并指出在准静态模式下，不规则性会提高内凹六边形蜂窝的能量吸收性能，但在高速冲击情况下，不规则性则会降低其能量吸收性能。

本文在文献[10]提出的旋转三角形变形构型基础上，针对不同旋转角建立了相应的蜂窝结构模型(本文称之为旋转三角形蜂窝)，并采用数值模拟的方法对这些蜂窝模型的动态压溃行为进行了研究。结果表明：当蜂窝旋转角在一定范围内变化时，这些蜂窝具有动态拉胀(或负泊松比)效应，其应力- 应变曲线具有 “两段式应力平台” 的特征，并且这种两段式平台应力的特征使其作为结构防护材料时具有更好的能量吸收能力。

1 几何模型和有限元模型

1.1 旋转三角形蜂窝的几何模型

图1给出了文献[10]中将刚性三角形通过弹性铰接而得到的旋转三角形模型。由图1可知，几何参数包括旋转角θ和等边三角形的边长l，当旋转角θ取0°、30°、60°、90°和120°时，可得到图1中的5种构型。显然，如果把图1中的刚性正三角形替换为可变形的薄壁正三角形(假设胞壁之间均为固接关系)，则可以得到图2中所示的5种蜂窝模型，其中θ为0°所对应的蜂窝壁厚为其余4种蜂窝壁厚的2倍。因此，基于不同旋转角的旋转三角形模型均可构建相应的旋转三角形蜂窝模型，但θ=0°和θ=120°分别对应了三角形蜂窝结构和kagome蜂窝结构。

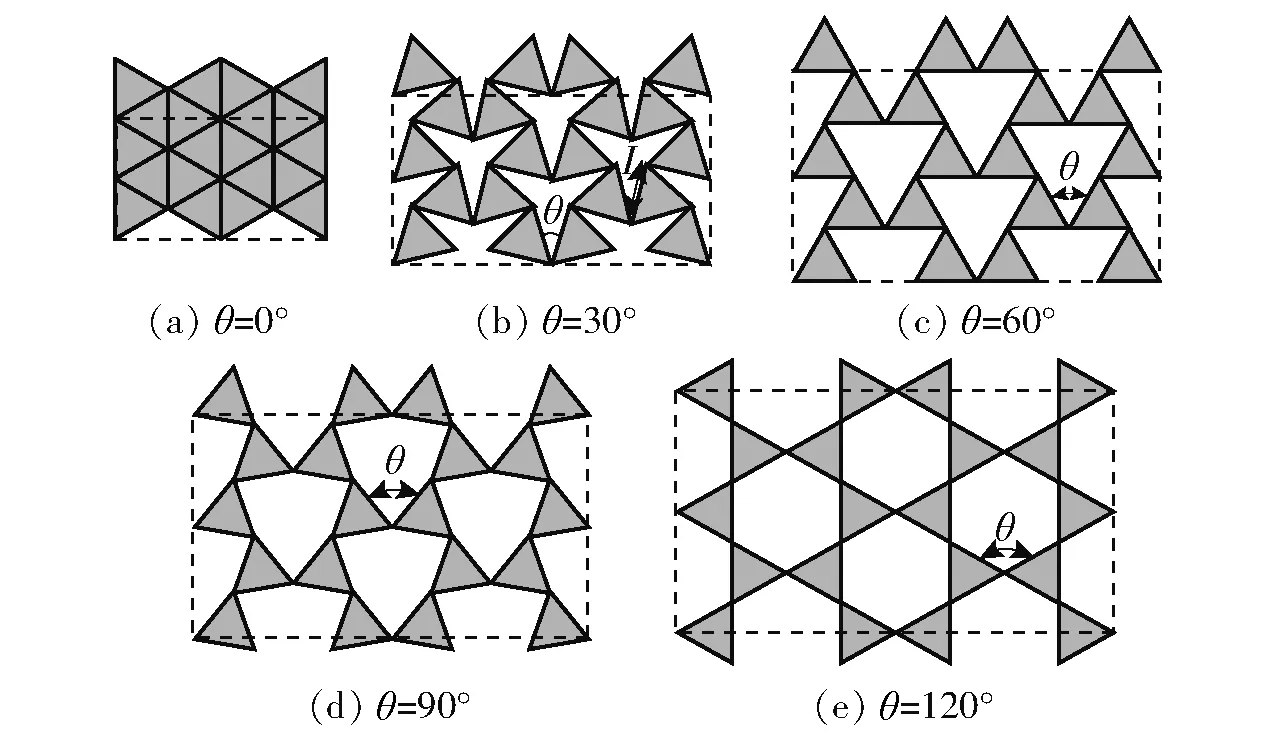
图1 旋转三角形几何模型[11]Fig.1 Geometric model of rotating triangles[11]

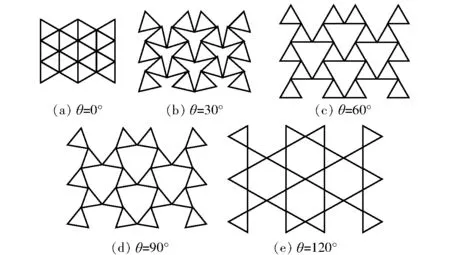
图2 基于旋转三角形的蜂窝模型Fig.2 Honeycomb models based on rotating triangles

1.2 旋转三角形蜂窝的有限元模型

图3给出了受冲击旋转三角形蜂窝的有限元模型，而其中左边的放大图给出了旋转三角形蜂窝的单胞模型。由图3可见，每个单胞由4个等边三角形构成，并组成左右对称的结构，其中h为胞壁的厚度。在本文所有算例中，取l=20 mm，h=1 mm，而θ的取值范围取为0～120°. 本文利用有限元分析软件ANSYS/LS-DYNA 对上述旋转三角形蜂窝模型的面内动态压溃行为进行了有限元建模和数值模拟研究。由图3的有限元模型可知，蜂窝模型在水平和竖直方向上均有10个单胞。在模拟中使用了SHELL163单元，单元尺寸取为2 mm，即每个三角形的边上分为10个单元。为了减少计算量，模型沿z方向的厚度与网格尺寸相同，即沿z方向只有一层壳单元。有限元模型选用的基体材料为金属铝，假设其本构行为符合理想弹塑性模型，密度ρ=2.7×103kg/m3，弹性模量E=70 GPa，泊松比μ=0.3，屈服应力σys=110 MPa. 将蜂窝的有限元模型置于上、下钢板之间，并约束所有节点的面外方向位移以模拟平面应变状态；同时，令下钢板固定，上钢板以恒定的速度v向下运动以模拟冲击过程。在模拟过程中对于蜂窝自身采用了单面自动接触算法，而钢板与蜂窝之间采用了面面自动接触算法，并假设所有接触为光滑接触。

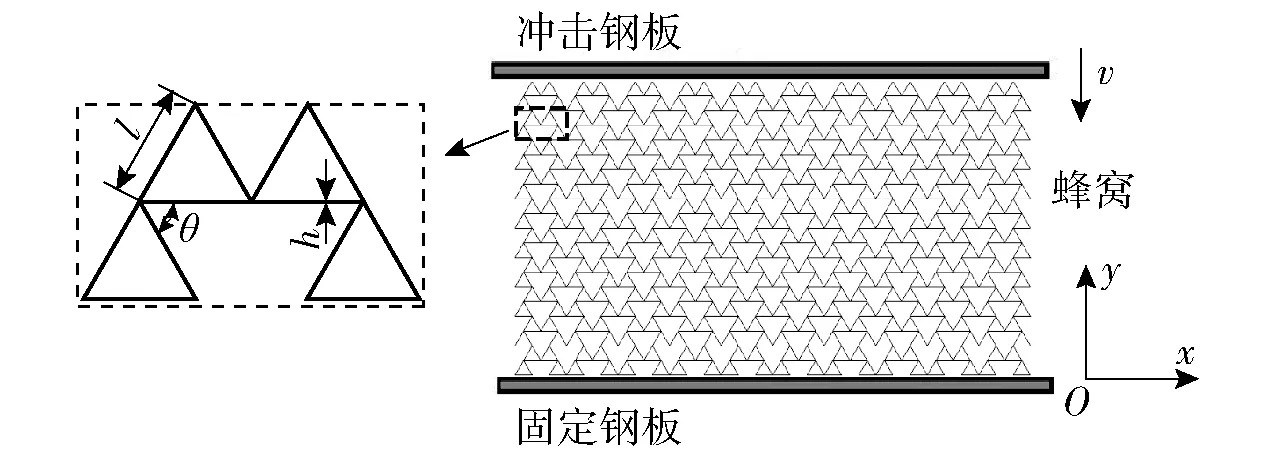
图3 蜂窝的单胞及有限元模型Fig.3 Unit cell and finite element model of honeycombs

2 结果与讨论

2.1 不同旋转角蜂窝的动态压溃行为

图4给出了旋转角为60°的旋转三角形蜂窝在1 m/s冲击速度下的变形模式图。由图4可见，旋转三角形蜂窝的坍塌变形主要分为两个阶段：第1阶段以单胞中三角形的旋转变形为主，当达到某一应变后，相邻的三角形胞壁相互接触、重叠，有使旋转三角形蜂窝变为正三角形蜂窝的趋势；第2个变形阶段则以正三角形的坍塌变形为主。图5给出了旋转角为60°的旋转三角形蜂窝在1 m/s冲击速度下的名义应力σ- 应变ε曲线。由图5可见，旋转三角形蜂窝的名义应力- 应变曲线具有“两个应力平台段”特征，第1个应力平台段对应着以正三角形旋转变形为主的变形阶段，而第2个应力平台段对应着以正三角形坍塌变形为主的变形阶段。这里，可以把旋转三角形蜂窝变为正三角形蜂窝时对应的应变值，或者把两个应力平台段分界点对应的应变值称之为临界应变。

图4 冲击速度为1 m/s时旋转三角形蜂窝(θ=60°)的变形模式Fig.4 Deformation modes of rotating triangle honeycombs (θ=60°) at the impact velocity of 1 m/s

图5 冲击速度为1 m/s时旋转三角形蜂窝(θ=60°)的名义应力- 应变曲线Fig.5 Nominal stress-strain curves of rotating triangle honeycombs (θ=60°) at the impact velocity of 1 m/s

图6给出了旋转角为60°的旋转三角形蜂窝在1 m/s冲击速度下的应力云图(名义应变为0.17)。由图6可知，在第1个变形阶段，三角形顶点处应力最大，故顶点处最先屈服并出现塑性铰，而塑性铰产生于三角形的顶点处正是单胞中三角形旋转变形的主要原因。

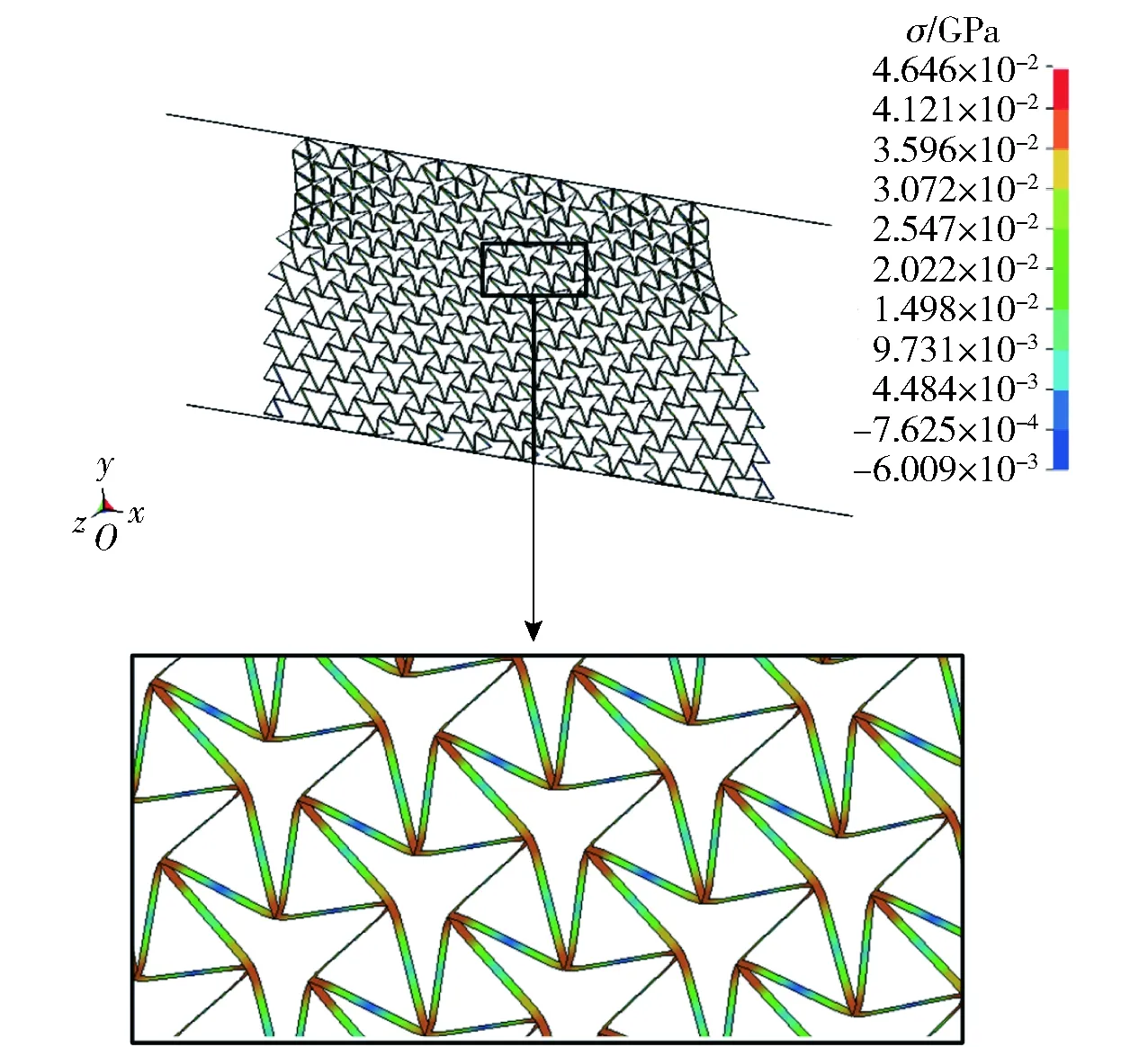
图6 冲击速度为1 m/s时旋转三角形蜂窝(θ=60°)的应力云图Fig.6 Stress nephogram of rotating triangle honeycombs (θ=60°) at the impact velocity of 1 m/s

当旋转角增大到一定程度时，由数值模拟结果不难发现：旋转三角形蜂窝的变形模式会发生一定的改变。图7和图8分别给出了旋转角为90°和100°的旋转三角形蜂窝在1 m/s冲击速度下的变形模式图。由图7可见，当旋转角为90°时，虽然旋转三角形蜂窝的变形依旧可分为两个阶段，但第1阶段不仅有正三角形的旋转变形，还包含着部分正三角形的坍塌变形。而当旋转角为100°时，如图8所示，两阶段特征的变形模式基本消失，整个变形过程基本上以正三角形的坍塌变形为主。对应旋转三角形蜂窝变形模式的改变，其相应的名义应力- 应变曲线也呈现了不同的规律。如图9(a)所示，当旋转角为90°时，相比旋转角为60°的情况(见图5)，由于第1变形阶段包含着部分正三角形的坍塌变形，所以相应的名义应力- 应变曲线的第1个应力平台段会持续更长的时间，而第2个应力平台段则会变短一些。但是，当旋转角为100°时，如图9(b)所示，因其变形模式不再具有两阶段特征，所以其名义应力- 应变曲线也就只表现为一个应力平台段。

图7 冲击速度为1 m/s时旋转三角形蜂窝(θ=90°)的变形模式Fig.7 Deformation modes of rotating triangle honeycombs (θ=90°) at the impact velocity of 1 m/s

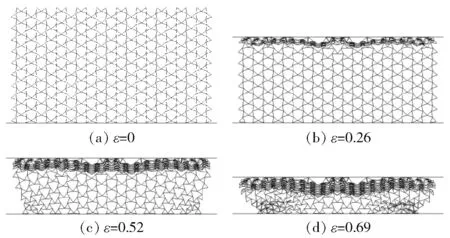
图8 冲击速度为1 m/s时旋转三角形蜂窝(θ=100°)的变形模式Fig.8 Deformation modes of rotating triangle honeycombs (θ=100°) at the impact velocity of 1 m/s

图10给出了冲击速度为1 m/s时旋转三角形蜂窝的第1段平台应力和第2段平台应力与旋转角间的关系。由图10可见，第1段平台应力随旋转角的变化很小，基本上维持在一个恒定的水平，而第2段平台应力则随旋转角增加而减小。当旋转角小于90°时，第2段平台应力减小的主要原因是随旋转角增大，蜂窝的初始尺寸增大，从而导致了名义应力的降低。当旋转角大于100°时，由于蜂窝的变形模式发生了变化，所以其名义应力- 应变曲线只呈现一个应力平台段。图11给出了冲击速度为1 m/s时临界应变随旋转角的变化情况。需指出，图11中理论临界应变指的是假定相邻正三角形的胞壁完全重叠，蜂窝变为规则的正三角形蜂窝时的名义应变。由于在实际变形过程中，蜂窝的胞壁不能完全重叠，所以临界应变一般应略小于理论的临界应变值。当旋转角接近90°时，由于在变形的初始阶段就伴随着部分正三角形的坍塌变形，所以其临界应变要大于理论的临界应变值。

图12给出了旋转三角形蜂窝动态泊松比随旋转角的变化情况，其中动态泊松比定义为旋转三角形蜂窝变形为正三角形蜂窝时横向收缩的名义应变与压缩名义应变的负比值。另外，图12中理论动态泊松比指的是假定相邻正三角形胞壁完全重叠时的动态泊松比。由于在实际变形过程中，胞壁间的横向间隙较大，所以动态泊松比的绝对值略小于理论动态泊松比。当旋转角接近90°时，由于其在变形为正三角形蜂窝时的压缩名义应变较大，所以其动态泊松比的绝对值要远小于理论动态泊松比。上述结果表明，当旋转角小于90°，且冲击速度较低时，旋转三角形蜂窝动态泊松比为负值，即蜂窝具有动态拉胀效应。

图9 冲击速度为1 m/s时旋转三角形蜂窝的名义应力- 应变曲线Fig.9 Nominal stress-strain curves of rotating triangle honeycombs at the impact velocity of 1 m/s

图10 平台应力随旋转角的变化Fig.10 Variation of plateau stress with rotating angles

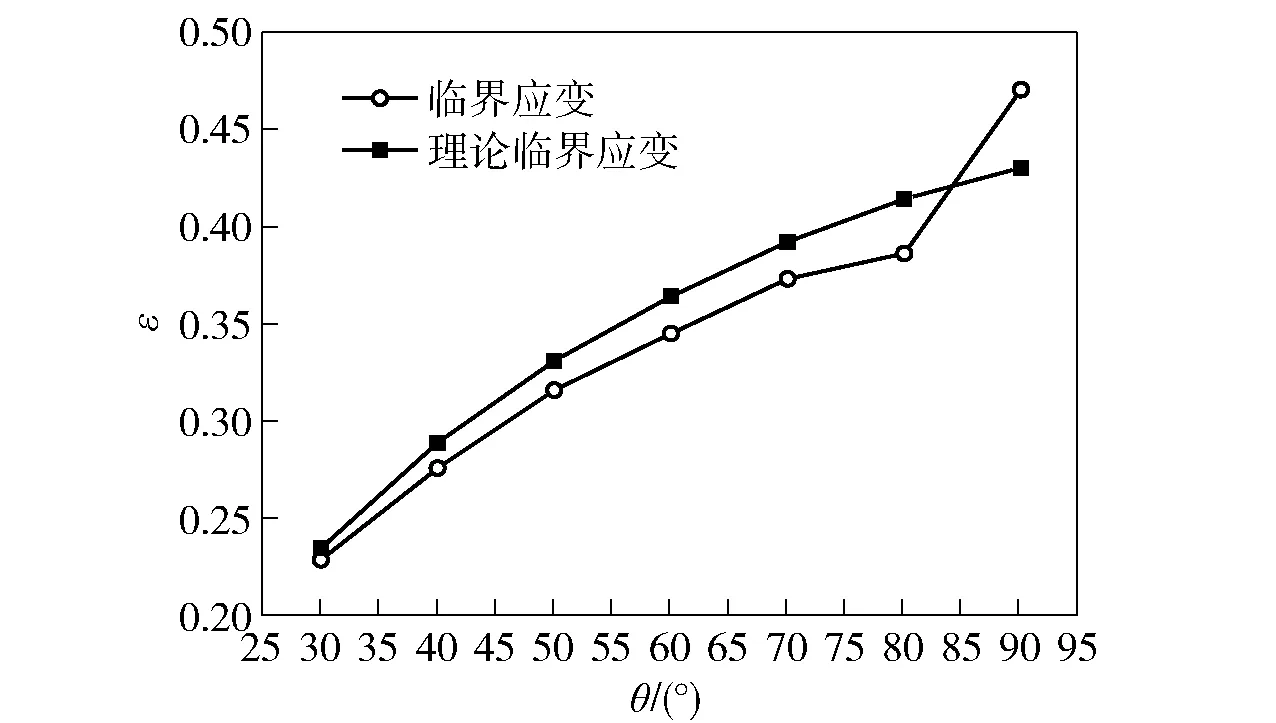
图11 临界应变随旋转角的变化Fig.11 Variation of critical strain with rotating angles

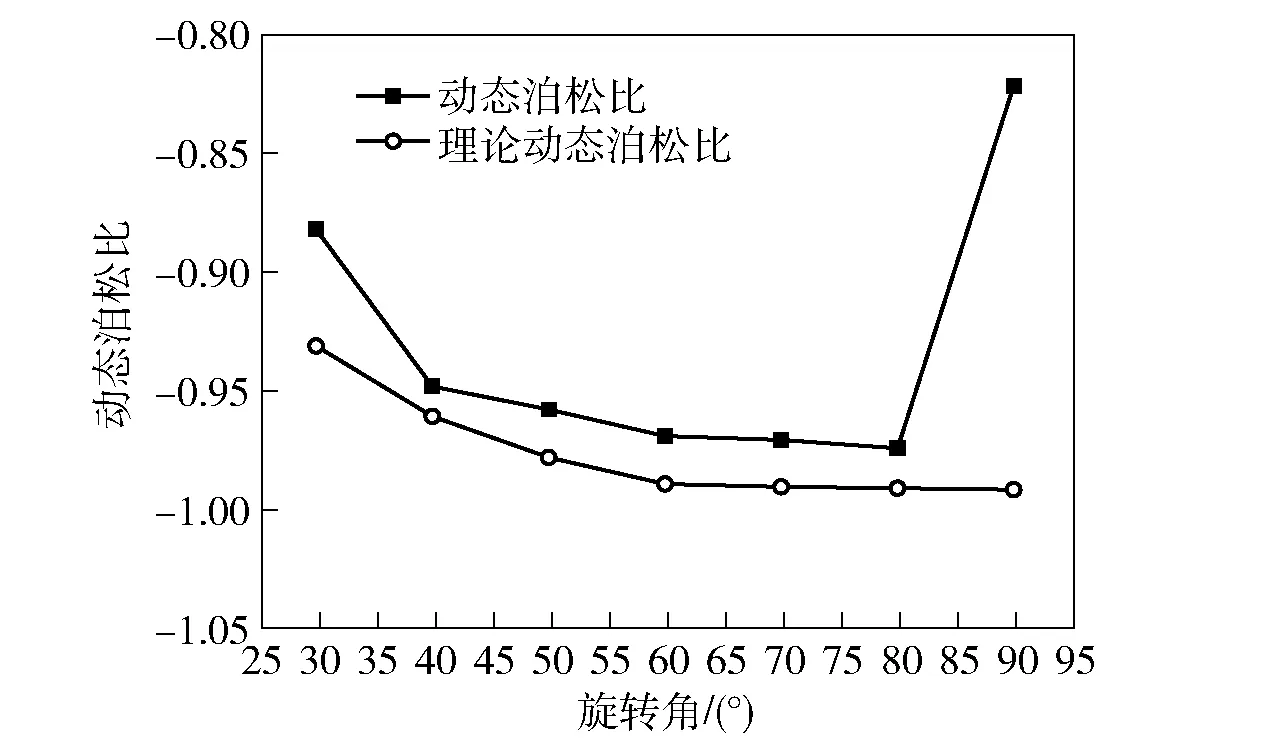
图12 动态泊松比随旋转角的变化Fig.12 Variation of dynamic Poisson’s ratios with rotating angles

2.2 不同冲击速度下旋转三角形蜂窝的动态压溃行为

图13和图14给出了旋转三角形蜂窝(θ=60°)在不同冲击速度下的变形模式图。由图4可见，当冲击速度较低时，在第1变形阶段，整体蜂窝以正三角形的旋转变形为主，基本上没有产生正三角形的坍塌变形。当冲击速度增加到30 m/s时(见图13)，在第1变形阶段，由于惯性效应的影响，冲击端处会产生局部的变形带，局部变形带内的正三角形以坍塌变形为主，而靠近固定端的正三角形以旋转变形为主，当应变达到临界应变值时，靠近固定端的部分蜂窝变形成正三角形蜂窝。而当冲击速度提高到60 m/s时(见图14)，旋转三角形蜂窝的变形模式主要表现为胞元的逐层坍塌模式，两阶段变形特征的模式基本消失。

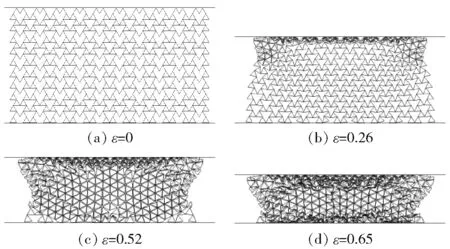
图13 冲击速度为30 m/s时旋转三角形蜂窝(θ=60°)的变形模式Fig.13 Deformation modes of rotating triangle honeycombs (θ=60°) at the impact velocity of 30 m/s

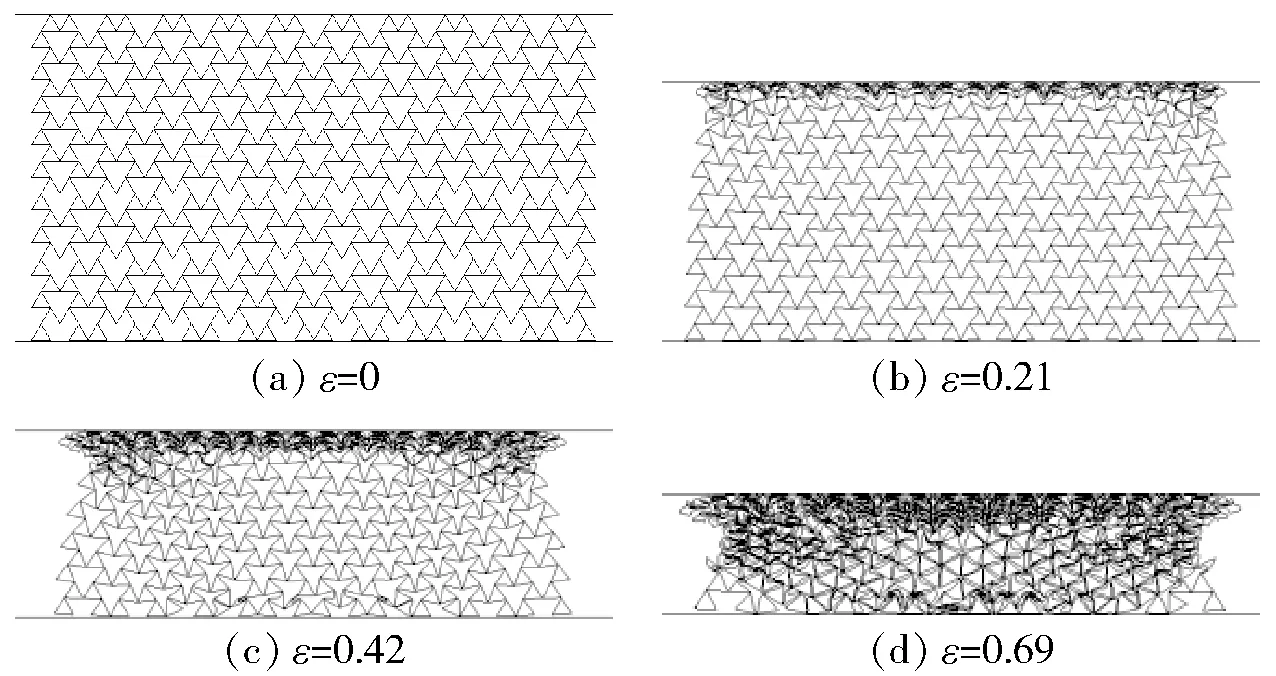
图14 冲击速度为60 m/s时旋转三角形蜂窝(θ=60°)的变形模式Fig.14 Deformation modes of rotating triangle honeycombs(θ=60°) at the impact velocity of 60 m/s

图15给出了旋转三角形蜂窝(θ=60°)在不同冲击速度下的名义应力- 应变曲线。由图15可见，随着冲击速度的提高，临界应变逐渐增大，名义应力- 应变曲线的第2个应力平台段逐渐变短直至消失。图16给出了旋转三角形蜂窝(θ=60°)临界应变随冲击速度的变化情况，可见，当冲击速度提高时，由于在冲击端会产生局部坍塌的变形带，所以实际的临界应变会大于低速情况下的理论临界应变。图17给出了旋转三角形蜂窝(θ=60°)的两阶段平台应力与冲击速度v的关系。由图17可见，随着冲击速度的提高，两阶段的平台应力整体上均呈现逐渐增大的趋势，但两者的差值却逐渐减小，当冲击速度超过60 m/s时，两阶段平台应力的特征基本消失。此外，图18给出了旋转三角形蜂窝(θ=60°)动态泊松比随冲击速度的变化情况。由图18可见，随着冲击速度的提高，冲击端处产生的局部变形胞元逐渐增多，使临界应变逐渐增大，从而导致动态泊松比的绝对值逐渐减小，即动态拉胀效应逐渐减弱。

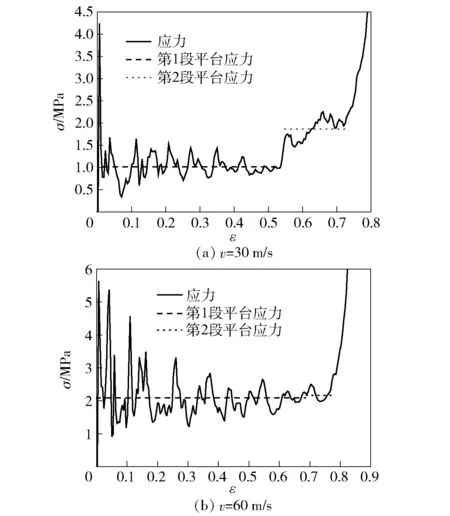
图15 不同冲击速度时旋转三角形蜂窝(θ=60°)的名义应力- 应变曲线Fig.15 Nominal stress-strain curves of rotating triangle honeycombs (θ=60°) at different impact velocities

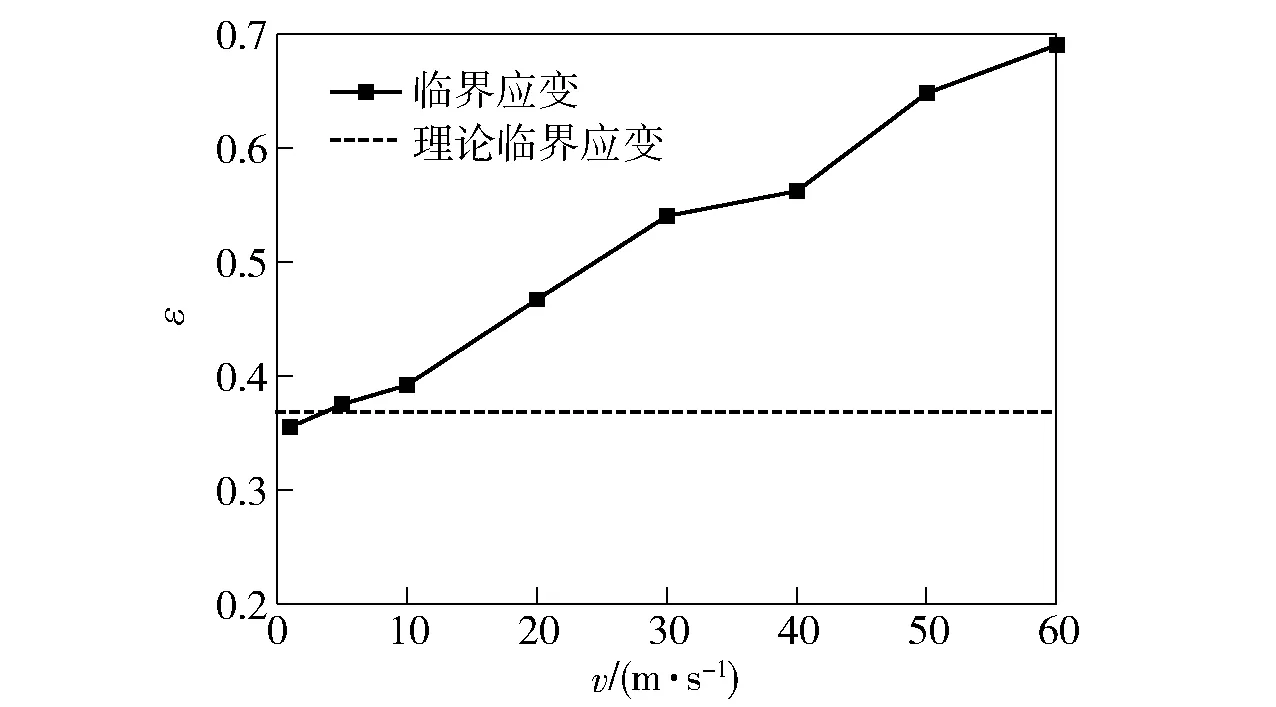
图16 旋转三角形蜂窝的临界应变随冲击速度变化Fig.16 Critical strain of rotating triangle honeycombs at different impact velocities

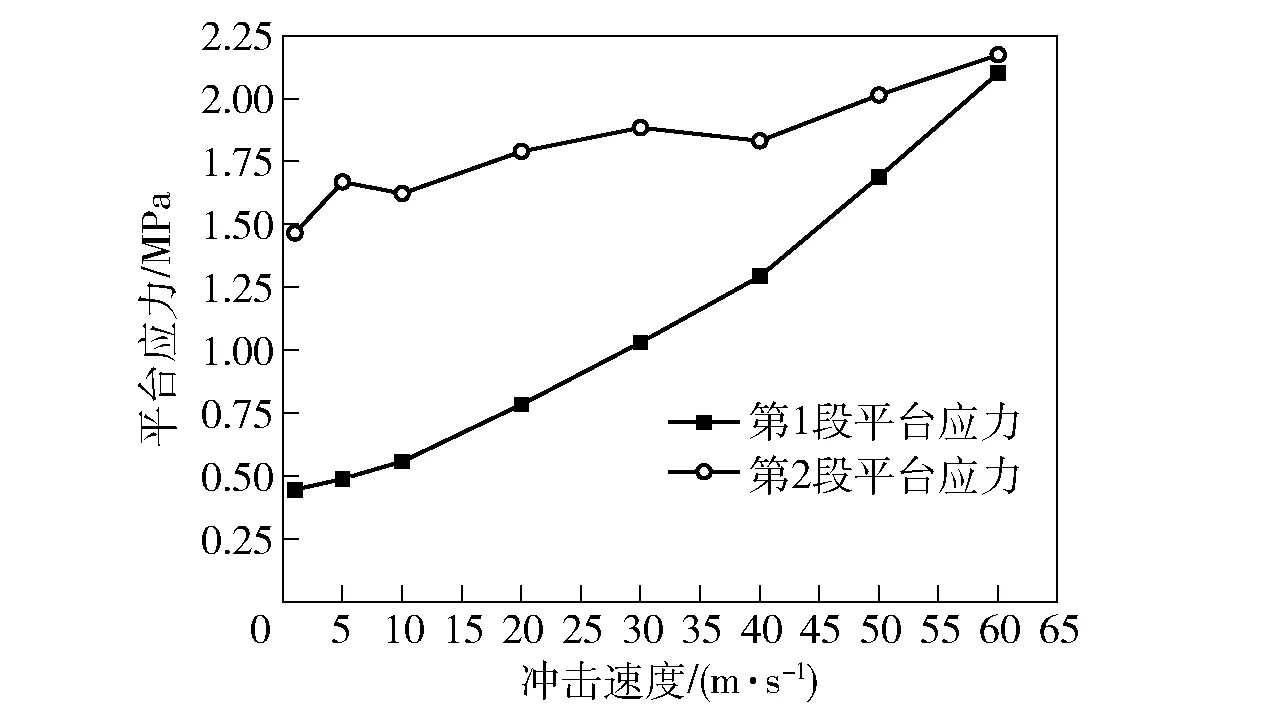
图17 旋转三角形蜂窝的平台应力随冲击速度变化Fig.17 Plateau stresses of rotating triangle honeycombs at different impact velocities

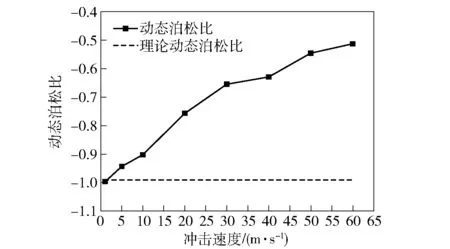
图18 动态泊松比随冲击速度变化Fig.18 Dynamic Poisson’s ratios of rotating triangle honeycombs at different impact velocities

2.3 旋转三角形蜂窝的能量吸收特性

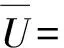
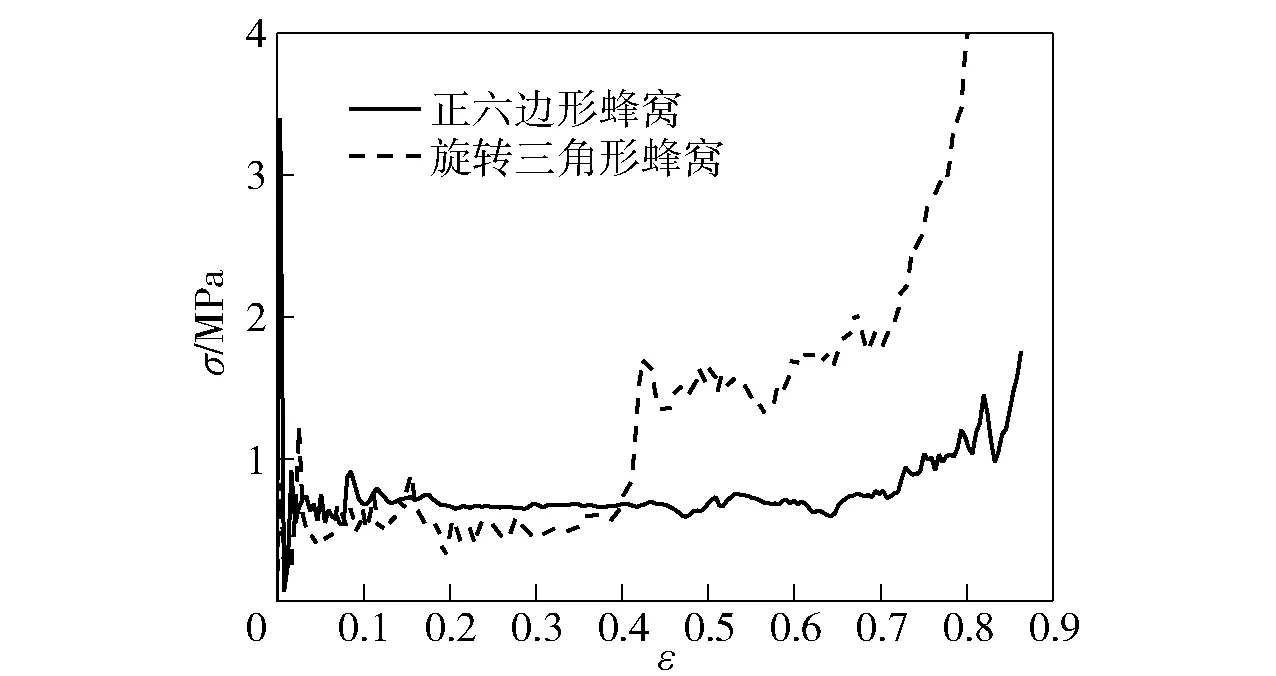
图19 旋转三角形蜂窝(θ=60°)与正六边形蜂窝的名义应力- 应变曲线Fig.19 Nominal stress-strain curves of rotating triangle honeycombs(θ=60°) and hexagonal honeycombs

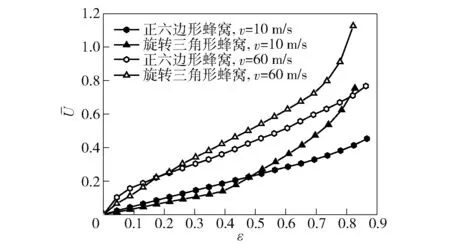
图20 旋转三角形蜂窝(θ=60°)与正六边形蜂窝的能量吸收性能Fig.20 Energy absorption curves of rotating triangle honeycombs (θ=60°) and hexagonal honeycombs

由图19可见，两种蜂窝在10 m/s冲击速度下的应力- 应变曲线特征存在明显差异，反映了两种蜂窝的变形机制的不同。不难看出，旋转三角形蜂窝的第1段平台应力略低于正六边形蜂窝的平台应力，而第2段平台应力却远高于正六边形蜂窝的平台应力。因此，在压缩量接近密实化应变时，旋转三角形蜂窝具有更强的能量吸收性能(见图20)。并且，当冲击速度较高时，例如，对于v=60 m/s的情况，虽然旋转三角形蜂窝不再具有两阶段平台应力的特征，但其平台应力要高于正六边形蜂窝，所以其能量吸收性能依然好于正六边形蜂窝(见图20)。

3 结论

本文基于文献[10]中的旋转三角形变形构型，提出了新的蜂窝结构模型，并采用有限元方法对这些新蜂窝的动态压溃行为进行了数值模拟研究，得到的主要结论如下：

1)在低速冲击下，旋转三角形蜂窝的变形过程可分为两个阶段：第1阶段以正三角形的旋转变形为主，第2阶段以正三角形的坍塌变形为主。旋转三角形蜂窝的动态压溃应力- 应变曲线具有两段式平台应力的特征，第2段的平台应力要高于第1段的平台应力。当旋转三角形蜂窝的旋转角超过90°时，这种两段式平台应力的特征逐渐消失，其应力- 应变曲线只有1个平台段。但是，当旋转三角形蜂窝的旋转角小于90°，且冲击速度较低时，旋转三角形蜂窝动态泊松比为负值，即旋转三角形蜂窝具有动态拉胀效应。

2)随着冲击速度的提高，两阶段的平台应力差值逐渐减小，且临界应变逐渐增大，动态拉胀效应逐渐减弱。当冲击速度超过60 m/s时，两段式平台应力的特征也基本消失。

3)在不同冲击速度下，与相对密度相同的正六边形蜂窝相比较，旋转三角形蜂窝均具有更好的能量吸收性能，该结论对蜂窝的抗冲击设计和应用具有重要意义。

)

[1] Gibson L J, Ashby M F. Cellular solids: structure and properties[M].2nd ed. Cambridge, UK: Cambridge University Press, 1997.

[2] Lira C,Scarpa F,Rajasekaran R. A gradient cellular core for aeroengine fan blades based on auxetic configurations[J]. Journal of Intelligent Material Systems & Structures, 2011, 22(9): 907-917.

[3] 张伟, 侯文彬, 胡平. 新型负泊松比多孔吸能盒平台区力学性能[J]. 复合材料学报, 2015(2): 534-541.

ZHANG Wei, HOU Wen-bin, HU Ping. Mechanical properties of new negative Poisson’s ratio crush box with cellular structure in plateau stage[J]. Acta Materiae Compositae Sinica, 2015(2): 534-541.(in Chinese)

[4] 卢子兴, 刘强, 杨振宇. 拉胀泡沫材料力学性能[J]. 宇航材料与工艺, 2010(1)：7-13.

LU Zi-xing, LIU Qiang, YANG Zhen-yu. Mechanical properties of auxetic foams[J]. Aerospace Materials & Technology, 2010(1):7-13.(in Chinese)

[5] 卢子兴, 李康. 负泊松比蜂窝动态压溃行为的有限元模拟[J]. 机械强度, 2016(6):1237-1242.

LU Zi-xing, LI Kang. Dynamic crushing of honeycombs with a negative Poisson’s ratio-a finite element study[J]. Journal of Mechanical Strength, 2016(6):1237-1242. (in Chinese)

[6] Larsen U D, Sigmund O, Bouwstra S. Design and fabrication of compliant micromechanisms and structures with negative Poisson’s ratio[J]. Journal of Microelectromechanical System, 1997, 6(2):99-106.

[7] Prall D, Lakes R S. Properties of a chiral honeycomb with a Poisson’s ratio of -1[J]. International Journal of Mechanical and Science, 1996, 39:305-314.

[8] 卢子兴, 赵亚斌. 一种有负泊松比效应的二维多胞材料力学模型[J]. 北京航空航天大学学报, 2006, 32(5)：594-597.

LU Zi-xing, ZHAO Ya-bin. Mechanical model of two-dimensional cellular materials with negative Poisson’s ratio[J].Journal of Beijing University of Aeronautics and Astronautics, 2006,32(5):594-597. (in Chinese)

[9] Lu Z X, Li X, Yang Z Y, et al. Novel structure with negative Poisson’s ratio and enhanced Young’s modulus[J]. Composite Structures, 2016, 138: 243-252.

[10] Lim T C. Auxetic materials and structures[M]. Singapore:Springer, 2015.

[11] Grima J N, Evans K E. Auxetic behavior from rotating triangles[J]. Journal of Materials Science, 2006, 41(10): 3193-3196.

[12] 张新春,刘颖,李娜. 具有负泊松比效应蜂窝材料的面内冲击动力学性能[J]. 爆炸与冲击, 2012, 32(5): 475-482.

ZHANG Xin-chun, LIU Ying, LI Na. In-plane dynamic crushing of honeycombs with negative Poisson’s ratio effects[J]. Explosion and Shock Waves, 2012, 32(5):475-482. (in Chinese)

[13] 卢子兴, 李康. 四边手性蜂窝动态压溃行为的数值模拟[J]. 爆炸与冲击, 2014, 34(2):181- 187.

LU Zi-xing, LI Kang. Numerical simulation on dynamic crushing behaviors of tetrachiral honeycombs[J]. Explosion and Shock Waves, 2014, 34(2):181-187. (in Chinese)

[14] Qiao J X, Chen C Q. Impact resistance of uniform and functionally graded auxetic double arrowhead honeycombs[J]. International Journal of Impact Engineering, 2015, 83: 47-58.

[15] Qiao J X, Chen C Q. Analyses on the in-plane impact resistance of auxetic double arrowhead honeycombs[J]. Journal of Applied Mechanics, 2015, 82(5):051007.

[16] Liu W Y, Wang N L, Luo T, et al. In-plane dynamic crushing of re-entrant auxetic cellular structure[J]. Materials & Design, 2016, 100: 84-91.

[17] 胡玲玲, 陈依骊. 三角形蜂窝在面内冲击荷载下的力学性能[J]. 振动与冲击, 2011, 30(5):226-229.

HU Ling-ling, CHEN Yi-li. Mechanical properties of triangular honeycombs under in-plane impact loading[J]. Journal of Vibration and Shock, 2011, 30(5): 226-229. (in Chinese)