基于自适应无迹卡尔曼滤波算法的多股螺旋弹簧动态响应模型参数辨识和分析

丁传俊， 张相炎， 刘宁

(南京理工大学 机械工程学院， 江苏 南京 210094)

0 引言

多股螺旋弹簧(简称多股簧)是由多股钢丝拧成钢索卷制而成的圆柱螺旋弹簧，如图1所示。和普通单股弹簧相比，多股簧抗冲击性能好、吸振能力强、具有较大的刚度和非线性阻尼、寿命长，常被用作为小口径自动武器的缓冲复进簧[1-2]。

图1 多股簧Fig.1 A stranded wire helical spring

由于构成弹簧的各股钢丝之间存在着复杂的接触(挤压)和摩擦，多股簧在加载过程中具有明显的非线性刚度和迟滞特性[2]。为描述这两种复杂的特性，文献[2-3]建立了多股簧的静态折线模型，但刚度上的突变难以真实地反映系统的加载和卸载特性；文献[4]提出了多股簧的动态修正Bouc-Wen模型，该模型作为光滑曲线模型，认为恢复力不仅与加载位移有关，还与加载路径有关。由于光滑曲线模型的恢复力与加载位移的光滑过渡特性比较符合实际，通过选择适当的模型参数可以构造出不同能耗、渐硬或渐软特性的迟滞模型，因此适合于多股簧建模。

Bouc-Wen模型及其修正模型是一个复杂的非线性迟滞模型，对其参数辨识存在一定的难度，目前主要的辨识算法大体上可以分为迭代算法[5-12]和解析算法[4,13]。文献[5]和文献[6]使用最小二乘法分别对结合面迟滞非线性模型和Kevlar绳索非对称迟滞模型进行了参数辨识；文献[7]和文献[8]分别使用无迹卡尔曼滤波(UKF)算法、约束UKF(CUKF)算法对工程结构的振动响应模型进行了参数辨识；文献[9]提出了辨识多股簧动态模型的两步法，其第2步使用迭代UKF(IUKF)算法可以辨识出迟滞部分的3个参数；文献[10-12]分别使用差分演进算法、神经网络优化算法和粒子云算法求解出迟滞模型的参数；文献[13]提出了一种无需迭代的解析算法，但该算法需要事先将恢复力的迟滞部分分离出来，而且只能辨识标准Bouc-Wen模型参数；文献[4]在文献[13]的基础上添加了局部优化算法，提出用于辨识非标准Bouc-Wen模型参数的三步法，其本质是解析算法和迭代算法的结合。

近些年来，基于点的高斯非线性自适应滤波算法在伺服系统控制、飞行器跟踪和模型参数在线辨识等领域获得了广泛的应用。文献[14]将自适应估计原理和模糊控制算法引入到UKF算法中，形成自适应联合UKF(AJUKF)算法，发现该算法能够很好地抑制初始化误差、系统噪声不确定性和环境异常扰动对机械臂故障探测和诊断过程的影响；通过使用自适应容积卡尔曼滤波(ACKF)算法，文献[15]有效地提高了陆基导航系统的导航精度；文献[16]基于协方差匹配原理，提出一种基于协方差匹配的自适应UKF滤波(CMAUKF)算法，并将其应用于飞行器的惯性导航系统(INS)与全球导航卫星系统(GNSS)集成导航，其结论是自适应滤波算法对具有状态突变的机动目标有很好的跟踪能力。

为了解决当前多股簧动态模型参数辨识过程中操作过程复杂、待辨识参数多和求解精度低等问题，本文提出了多股簧参数辨识的自适应UKF滤波(AUKF)算法。该算法基于极大后验估计原理(MAP)和指数加权衰减原理[17]，能够对多股簧试验数据中的量测(过程)噪声进行递推和估计，确保非线性模型参数辨识的收敛性。AUKF算法既不需要对试验数据进行平滑处理，也不需要事先分离恢复力的迟滞部分，可辨识参数数量多且速度快、精度高。通过对某自动武器的复进簧进行动态加载试验并对含有量测噪声的试验数据进行测试，验证了本文算法的准确性和有效性。

1 AUKF算法

UKF算法通过构造一组可调权重的采样点，并通过非线性函数传播来估计系统状态的均值和协方差，滤波精度至少可以达到2阶。但在实际使用过程中，这种滤波算法对初始值的选取比较敏感，需多次调节初始参数才能获得较好的结果。此外，由于动力学模型和试验过程存在不确定性，噪声统计特性易发生变化，UKF算法由于本身不具备应对噪声统计变化的调节能力，容易出现滤波精度下降甚至发散。AUKF算法作为UKF算法的改进，通过实时递推计算并更新量测噪声(过程噪声)可以有效地提高参数辨识过程的计算精度和数值稳定性。

设系统的非线性状态方程和观测方程分别为

(1)

式中：xk与zk分别为状态向量和量测向量；f(xk-1)与h(xk)分别是非线性状态函数和量测函数；wk-1和vk是分别服从于N(q,Q)和N(r,R)的系统噪声和观测噪声，它们是互不相关的高斯白噪声，其中q、Q、r、R分别为系统噪声和观测噪声的均值及协方差。

初始状态x0和wk-1、vk互不相关，且服从高斯正态分布，其均值和协方差矩阵为

(2)

为了提高AUKF算法的收敛能力，首先将系统状态向量和协方差矩阵进行增广处理[18]：

(3)

式中：q0、Q0是系统状态噪声的初始均值及初始协方差矩阵。

AUKF算法的具体流程如下：

1)初始化。使用(4)式计算(2nS+1)个Sigma点及其相应的权值：

(4)

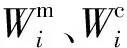
2)时间更新。采用无迹变换对每个Sigma点进行非线性变换，并计算变换后的均值和协方差矩阵：

(5)

3)观测更新。采用无迹变换对系统的观测进行更新：

(6)

4)状态增广。使用卡尔曼增益对系统的均值和协方差矩阵进行更新，得到后验的状态估计：

(7)

5) 噪声估计。文献[17]证明了基于MAP的常值噪声估计器的无偏性。当系统模型的不确定性较大或者状态发生突变时，基于极大后验准则、带噪声估计器的AUKF算法可以在滤波过程中利用测量数据对噪声特性进行实时动态估计，然后将得到的噪声信息用于UKF算法的状态参数估算，最终获得次优系统状态估计值。当噪声统计变化较慢时，可以采用渐消记忆指数加权来强调新近数据的作用，即对新近的噪声信息乘以渐消记忆因子dk. 因此，k时刻渐消记忆时变噪声统计估计器k、k、k和k的递推公式为

(8)

式中：εk为测量结果的预测误差；b为遗忘因子，取值范围一般为0.95≤b≤0.99. 若k和k在计算过程中为负值，则使用(9)式进行替代计算：

(9)

2 多股簧的非线性响应模型及AUKF算法计算初始化

2.1 标准化Bouc-Wen迟滞模型

文献[13]认为经典Bouc-Wen模型存在冗余参数，并提出精简参数的标准化Bouc-Wen迟滞模型，其数学表达式为

(10)

式中：F(t)为弹簧的恢复力；x(t)、t分别为位移和时间；κx、κω分别为屈服后刚度系数和迟滞部分初始刚度；ω(t)为纯迟滞分量，对于任意的x(t)，都有|ω(t)|≤1；ρ、σ、n为控制纯迟滞分量ω曲线形状的迟滞三参数。文献[13]进一步指出标准化Bouc-Wen模型只有在满足σ≥0.5时才有物理意义，而且在实际应用中，若n<1则会使微分方程的右端出现无限大的量，从而导致计算发散。

2.2 修正的标准化Bouc-Wen迟滞模型

为了获得迟滞模型的非对称曲线，文献[4]提出使用非线性刚度系数和非线性放大因子来代替标准化模型中的线性屈服后刚度系数和迟滞部分初始刚度，两者均用多项式表示：

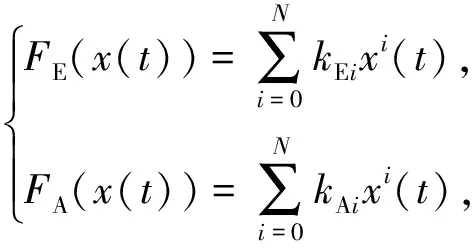
(11)

式中：FE和FA分别是恢复力的非线性弹性部分和非线性放大部分；kEi和kAi分别是非线性刚度系数和非线性放大因子；N是多项式的阶数，一般取2阶或3阶。

从而得到可以描述多股簧动态响应的修正标准化Bouc-Wen迟滞模型：

(12)

2.3 方程离散及计算参数初始化

当前算法需要定义系统的状态向量x为

x=[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10]T=
[kE0,kE1,kE2,kA0,kA1,kA2,ω,ρ,σ,n]T.

(13)

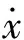
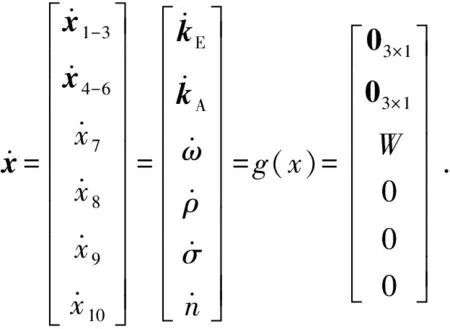
(14)

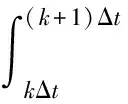
(15)

与此对应的系统离散观测方程为

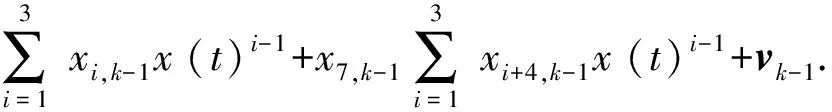
(16)

因为部分模型参数有界限约束(σ≥0.5、n≥1)，所以设置初始状态估计值为

0=-100,10,1,100,10,1,1,5,50,5T.

(17)

设置初始状态协方差矩阵为

P0=diag(100,100,100,100,100,100,1,1,10,1).

(18)

文献[17]建议过程噪声和量测噪声不要同时更新，否则滤波精度将会变差。由于系统的动力学模型比较确定，而对动态试验过程中的量测噪声统计特性不太肯定，因此本算法不更新过程噪声的统计特性；过程噪声的均值和协方差矩阵分别设定为q0=qk=01×10、Q0=Qk=10-5I10，量测噪声的初始均值和协方差分别设定为r0=0、R0=10.

3 多股簧力学试验

当前动力学试验装置为瑞士w+b公司生产的动态疲劳试验机，试验装置如图2所示。两根性质相同的多股簧被安装在上、下夹持件之间，并穿过各自的导杆以防止在加载过程中弯曲；下夹持件在试验过程中保持固定，上夹持件通过试验机夹头施加简谐激励信号x(t)。多股簧的变形量为上夹头的位移，多股簧恢复力通过下夹头下的传感器测得。

当前试验的多股簧为某自动武器的复进簧，长600 mm，弹簧外径19.5 mm；弹簧由4根高级碳素弹簧钢钢丝绕制而成，钢丝直径为1.6 mm. 由于自动武器中的多股簧只能承受压缩变形，所以在试验之前对多股簧施加了260 mm的预压量，从而保证多股簧在试验中一直处于压缩状态。当前动态试验对多股簧按照一定的幅值和频率循环加载，加载幅值从20 mm到45 mm不等，加载频率从0.05 Hz到1.50 Hz不等，系统的采样频率为1 kHz，图3即为不同加载幅值下、加载频率为0.50 Hz时测得的复进簧响应曲线。

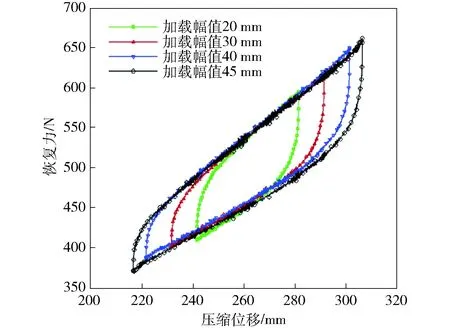
图3 实测的多股簧响应Fig.3 Measured responses of stranded wire helical spring

4 参数辨识结果和分析

4.1 参数辨识结果

将第3节试验输出的位移、恢复力数据输入到AUKF算法中即可对多股簧的模型参数进行递推计算。为检验当前参数辨识算法的有效性，本文将对比文献[9]所用的两步法(两步法首先采用最小二乘法求得非迟滞部分参数，再使用IUKF算法求解迟滞部分三参数)、文献[4]提出的三步法(三步法首先采用最小二乘法求得非迟滞部分参数，再使用解析法求解迟滞部分三参数，最后对全部参数进行优化)、文献[10]提出的差分演进算法(固定参数n的值)。

图5 系统状态的估计值Fig.5 Estimation of system states

量测噪声统计估计值、系统状态的估计值分别如图4和图5所示。从图4中可以看出，在滤波初期，因量测噪声的统计未知或不准确，系统各个状态的估计值波动较小，但随着基于渐消记忆加权的噪声统计估计器从加载位移换向时刻(0.5 s前后)开始对量测噪声均值r和方差R进行有效跟踪，各个状态的估计值逐渐趋于收敛，AUKF算法对各个状态的滤波效果由坏转好。在加载换向之前，多股簧实测数据中的迟滞量ω≈1，由于响应模型中系统初值ω设定为1，因此滤波过程前期并没有体现出应有的效果；而在加载换向时迟滞量ω≠1，由于和系统初值相差较大，AUKF算法迭代时出现一定的波动。当滤波过程趋于平稳后，此时量测噪声均值r、协方差R的范数稳态值分别约为0.157和2.5.

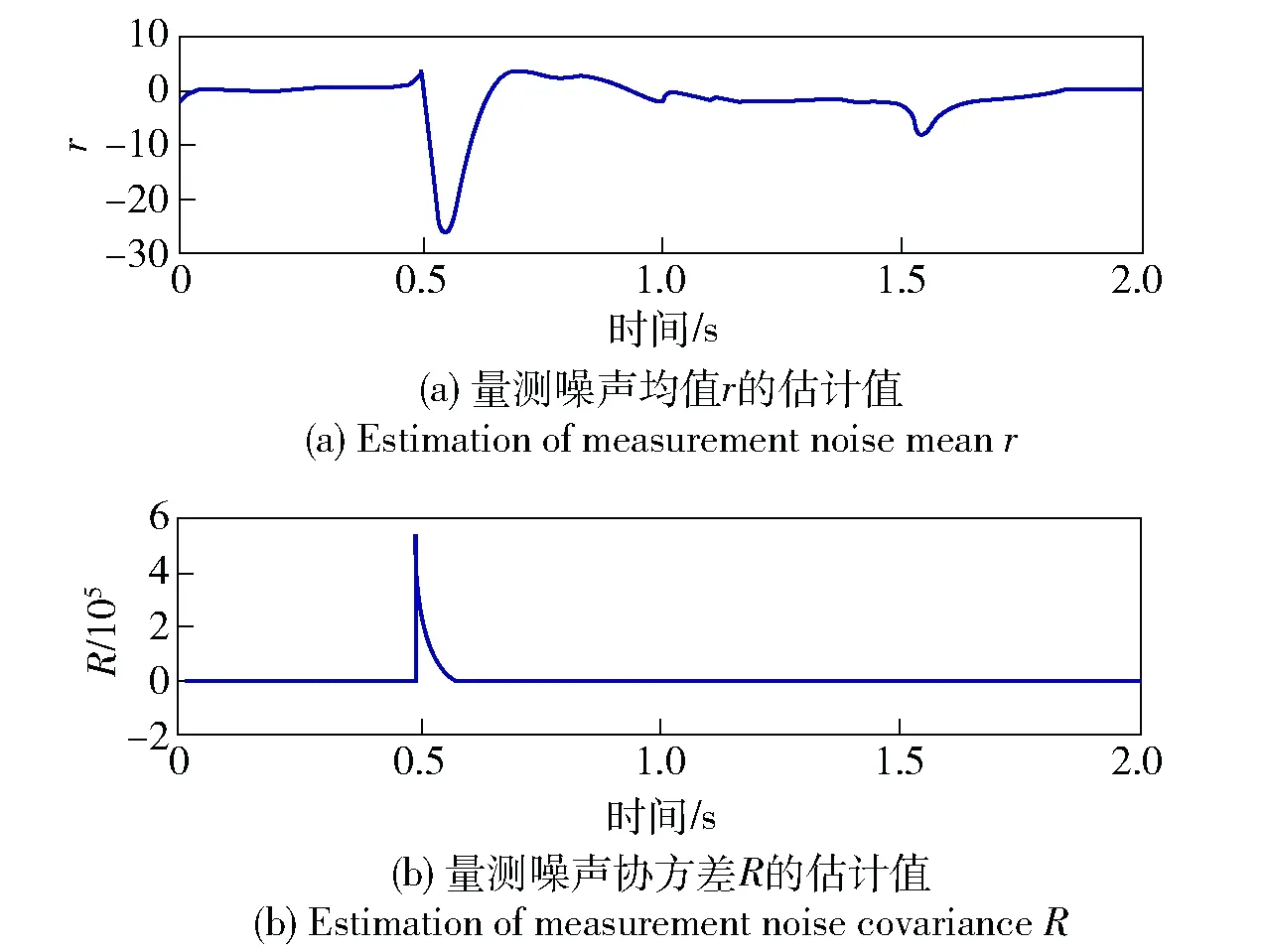
图4 量测噪声的统计特性Fig.4 Measurement noise statistics

为了能够定量分析参数辨识的效果并方便和其他几种算法对比，本文使用参数辨识结果仿真出来的恢复力和试验数据来计算恢复力的均方根误差(RMSE)：

(19)

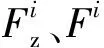
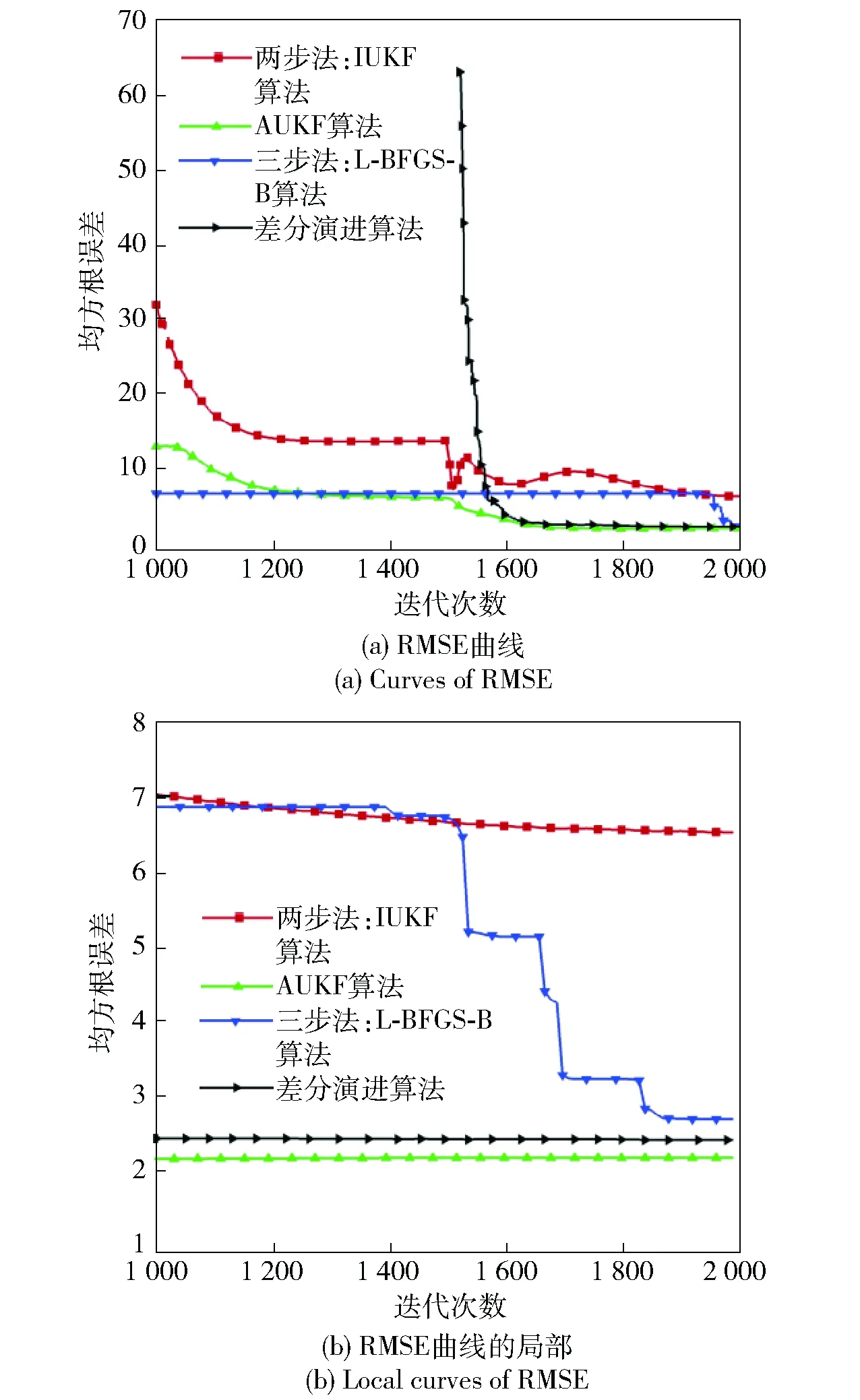
图6 4种算法的误差曲线Fig.6 Estimated error curves of four algorithms

从图5、图6和表1中可以看出，由于AUKF算法通过直接对迟滞部分和非迟滞部分参数进行递推求解，不仅所需时间最少，而且计算精度也较两步法提高了1倍以上，这说明精确计算量测噪声统计特性的重要性。虽然AUKF算法辨识出的非线性刚度系数和非线性放大因子趋近于两步法获得的结果，但从精度上来说，AUKF算法辨识的结果高于两步法的结果，其原因在于AUKF算法求解前不需要对数据进行平滑、节选处理；两步法的第2步中含有迭代过程，耗时有所增加且精度不佳，在量测噪声统计特性未知或者不准确时，迟滞参数ρ持续波动、σ和n陷入停滞，算法最终无法准确求解出迟滞部分参数，滤波精度严重下降以至于和试验结果有较大的偏差；三步法和差分演进算法虽然都能获得较好的精度，但都比较耗时。而且两步法和三步法都需要在计算之前对数据平滑降噪和分离处理，如果试验时加载的幅值较小，则所分离的迟滞部分将含有较大的误差。

表1 4种算法的RMSE和耗时的对比

4.2 量测噪声对参数辨识精度的影响

为了分析噪声对AUKF算法参数辨识过程的影响，本文对实测恢复力数据添加了不同强度级别的噪声，噪声等级C分别为取为0.01、0.03、0.05、0.07，带噪声数据的生成表达式为

Fc=F0+CArRn，

(20)

式中：Rn为标准正态分布的随机数向量；Ar为试验数据F0的幅值，

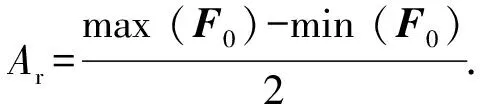
(21)

将含有噪声的数据(幅值40 mm)代入AUKF算法，辨识结果如图7所示。从图7(c)和图7(d)中可以看出，即使在量测噪声较高的情况下，AUKF算法辨识的结果依然能够较为精确地匹配试验数据；但是随着噪声等级的增加，辨识出来的恢复力- 位移曲线的光滑性变差，特别是在位移换向之后的加载过程中。AUKF算法辨识出的参数如表2所示，可以看出迟滞部分3个参数随着噪声等级的增加而持续增大，其中σ的收敛性变差，已经偏离无噪声时的最优解，但非迟滞部分参数基本不变(为了表述的简洁性，表2已将kEi和kAi按照x的升幂写成向量形式kE和kA)。

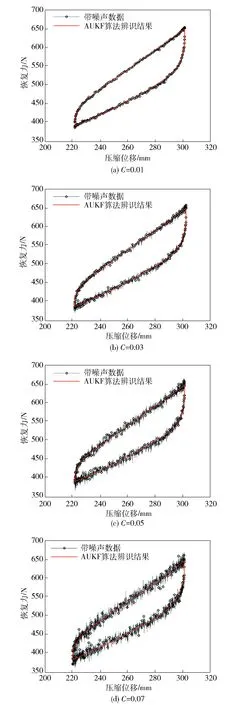
图7 不同噪声级别下的预测响应Fig.7 Predicted responses under different noise levels

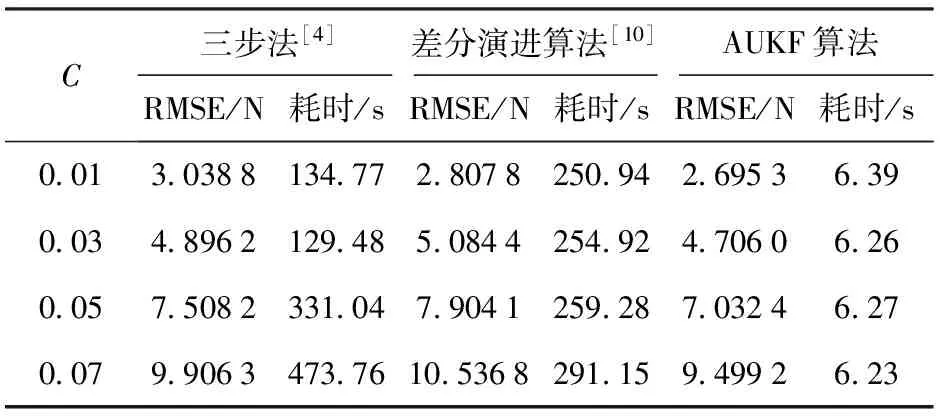
与此同时，本文也对比了其他算法在不同噪声级别下的表现。由于两步法对试验数据的平滑特性要求较高，当噪声等级超过一定程度时(C=0.03)，计算过程会因为求解矩阵出现负定而中断，因此本文算法只和三步法、差分演进算法的求解结果相对比。从表3中可以看出，AUKF算法所辨识的参数精度均高于其他两种算法，但AUKF算法的耗时基本不变；随着噪声等级的增大，三步法和差分演进算法的耗时都有所增加，而且差分演进算法经常会因为参数陷入局部解而导致求解过程停滞。有必要说明的是，当前带噪声统计估计器的AUKF算法只适用于噪声为加性白噪声的非线性系统；在参数设置方面，AUKF算法对迟滞三参数的初始状态误差协方差的选择比较敏感。

4.3 多股簧动态响应的预测误差分析

文献[4]和文献[9]认为多股簧的动态响应具有区间重叠特性，即较大振幅试验数据所辨识的参数可以用来预测较小振幅的多股簧响应。为了验证这一结论，本文基于45 mm幅值(振动频率0.50 Hz)的试验数据所辨识的参数分别来预测40 mm、30 mm、20 mm振幅下的响应，其RMSE分别为5.961 3 N、6.371 3 N、8.326 7 N. 从图8中可以看出，小振幅情况下的试验结果和预测结果差别比较大，主要体现在位移换向的两端。出现这种误差的原因在于小振幅下的多股簧簧丝在大部分加载过程中处于拧紧和相互挤压状态，簧丝之间的相对运动有所减少，弹簧内部的摩擦耗能有所降低，从而导致迟滞三参数发生改变。因此基于当前试验结果，本文认为上面结论的适用范围是，动态情况下所要预测的多股簧响应，其振幅不能和参数辨识所用的振幅相差太大，即幅值的减少量应当控制在一个合理的范围内。

4.4 加载速度对非迟滞部分参数的影响

文献[19]认为加载速度的增大会改变多股簧簧丝之间的接触和摩擦特性，从而使多股簧的模型参数发生变化。为了研究多股簧动态模型参数的变化特性，本文进行了不同振动频率的加载试验。加载幅值为20 mm，振动频率分别为0.05 Hz、0.10 Hz、0.50 Hz、1.00 Hz、1.50 Hz，其对应的初始速度分别为6.83 mm/s、13.56 mm/s、72.25 mm/s、144.17 mm/s、214.99 mm/s. 使用AUKF算法对试验结果进行参数辨识后发现，迟滞三参数的变化不大，因此表4中只列出对应的非线性刚度系数和非线性放大因子。从表4中得知，随着加载速度的增大，AUKF算法的预测误差也逐渐增大，这说明随着速度的增加，试验系统的量测噪声也在增大；与此同时，0阶非线性刚度系数有所增大，0阶非线性放大因子持续降低，而其他参数变化较小。因此本文认为，对于特定的多股簧，若使用修正标准化Bouc-Wen模型，则其动态响应模型中的迟滞三参数一般可以取为定值，而非线性刚度系数和非线性放大因子则随着加载速度的变化而变化。

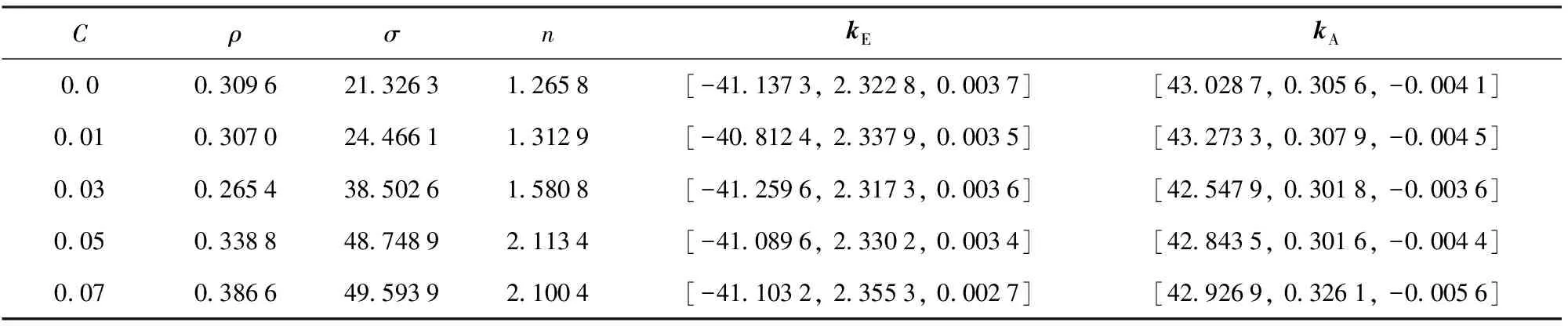
表2 不同噪声级别下AUKF算法辨识的多股簧参数

表3 不同噪声级别下3种算法的预测响应RMSE和耗时的对比

Tab.3 Comparison of predicted response RMSEs and running times of three algorithms under different noise levels

C三步法[4]差分演进算法[10]AUKF算法RMSE/N耗时/sRMSE/N耗时/sRMSE/N耗时/s00130388134772807825094269536390034896212948508442549247060626005750823310479041259287032462700799063473761053682911594992623

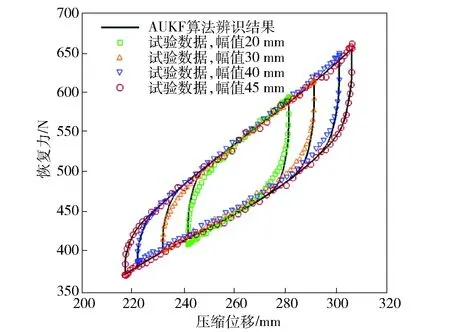
图8 实测响应和AUKF算法预测响应Fig.8 Measured and predicted responses by AUKF

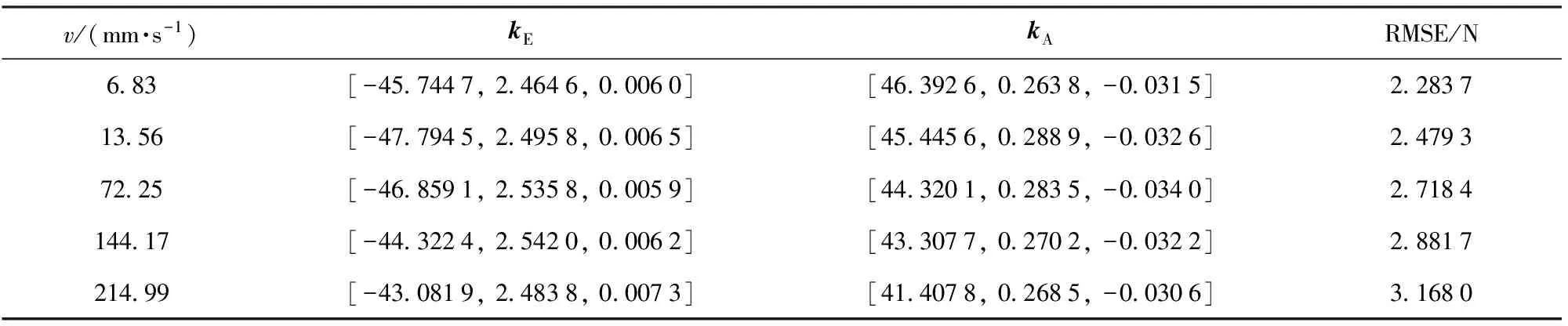
表4 非线性刚度系数和非线性放大因子的辨识结果

5 结论

1)基于修正的标准化Bouc-Wen模型，本文提出多股簧动态响应模型参数辨识的AUKF算法，该算法在滤波计算的同时，利用噪声统计估计器对未知的噪声特性进行实时估计和修正，有效地提高了参数辨识的速度和精度。

2)随着量测噪声等级的增大，使用AUKF算法辨识参数时，参数σ和n的收敛性逐渐变差，而非线性刚度系数和非线性放大因子几乎不受影响。

3)通过试验发现，动态情况下所要预测的多股簧响应，若其振幅和参数辨识所用的振幅相差太大，则导致较大的预测误差。

4)使用修正的标准化Bouc-Wen模型时，多股簧非线性刚度系数和非线性放大因子与速度有关。从当前低速动态试验的结果来看，0阶非线性刚度系数有所增大，0阶非线性放大因子逐渐减小，而其他参数变化较小。

致谢：中国空气动力研究与发展中心的赵煜博士在本文构思过程中提出了许多宝贵意见，作者对此表示非常感谢。

)

[1] 于道文. 多股螺旋弹簧的动应力及其有效寿命[J].南京理工大学学报, 1994 (3): 24-29.

YU Dao-wen. Dynamic stress of stranded wire helical spring and its useful life[J]. Journal of Nanjing University of Science and Technology, 1994 (3): 24-29. (in Chinese)

[2] 王时龙, 周杰, 李小勇, 等. 多股螺旋弹簧[M].北京: 科学出版社, 2011: 47-51.

WANG Shi-long, ZHOU Jie, LI Xiao-yong, et al. Stranded wire helical spring[M]. Beijing: Science Press, 2011: 47-51. (in Chinese)

[3] 闵建军, 王时龙. 多股螺旋弹簧动态计算分析[J].机械工程学报, 2007, 43(3): 199-203.

MIN Jian-jun, WANG Shi-long. Dynamic design method for stranded wire helical spring [J]. Chinese Journal of Mechanical Engineering, 2007, 43(3): 199-203. (in Chinese)

[4] Zhao Y, Wang S L, Zhou J, et al. Three-stage method for identifying the dynamic model parameters of stranded wire helical springs[J]. Chinese Journal of Mechanical Engineering, 2015, 28(1): 197-207.

[5] 李玲,蔡安江, 蔡立刚, 等. 基于Bouc-Wen模型辨识结合面动态特性研究[J]. 振动与冲击, 2013, 32(20): 139-144.

LI Ling, CAI An-jiang, CAI Li-gang, et al. Dynamic characteristics identification of joint interfaces based on a Bouc-Wen model[J]. Journal of Vibration and Shock, 2013, 32(20): 139-144. (in Chinese)

[6] 易琳, 王班, 郭吉丰. Kevlar绳索非对称迟滞模型及参数识别[J]. 浙江大学学报:工学版, 2015, 49(7): 1376-1381.

YI Lin, WANG Ban, GUO Ji-feng. Modeling and identification of asymmetric hysteresis for Kevlar tether[J]. Journal of Zhejiang University:Engineering Science, 2015, 49(7): 1376-1381. (in Chinese)

[7] 韩强, 董慧慧, 郭婕. 考虑强度和刚度退化及捏拢效应的钢筋混凝土桥墩滞回模型及其参数识别[J]. 振动工程学报, 2015, 28(3): 381-393.

HAN Qiang, DONG Hui-hui, GUO Jie. Hysteresis model and parameter identification of RC bridge piers considering strength and stiffness degradation and pinching effect[J]. Journal of Vibration Engineering, 2015, 28(3): 381-393. (in Chinese)

[8] 王涛, 吴斌, 孟丽岩, 等. 约束UKF初始参数对Bouc-Wen模型参数识别的影响[J]. 黑龙江科技大学学报, 2014, 24(6): 651-657.

WANG Tao, WU Bin, MENG Li-yan, et al. Effects of initial parameters of constrained UKF on parameter identification for Bouc-Wen model[J]. Journal of Heilongjiang University of Science and Technology, 2014, 24(6): 651-657. (in Chinese)

[9] 程成. 周期载荷下多股簧的动力学模型及响应特性研究[D]. 重庆: 重庆大学, 2014: 30-44.

CHENG Cheng. Study of modeling and responses characteristics of stranded wire helical spring under periodic loading[D]. Chongqing: Chongqing University, 2014: 30-44. (in Chinese)

[10] Worden K, Manson G. On the identification of hysteretic systems. Part I: fitness landscapes and evolutionary identification[J]. Mechanical Systems and Signal Processing, 2012, 29(5): 201-212.

[11] Fu Z J, Xie W F, Luo W D. Robust on-line nonlinear systems identification using multilayer dynamic neural networks with two-time scales[J]. Neurocomputing, 2013, 113(7): 16-26.

[12] Quaranta G, Marano G C, Greco R, et al. Parametric identification of seismic isolators using differential evolution and particle swarm optimization[J]. Applied Soft Computing, 2014, 22(5): 458-464.

[13] Ikhouane F, Rodellar J. On the hysteretic Bouc-Wen model[J]. Nonlinear Dynamics, 2005, 42(1): 79-95.

[14] Shabbouei H Y, Mohammadi A R, Cocquempot V. A hybrid robust fault tolerant control based on adaptive joint unscented Kalman filter[J]. ISA Transactions, 2017, 66: 262-274.

[15] Liu M, Lai J Z, Li Z M, et al. An adaptive cubature Kalman filter algorithm for inertial and land-based navigation system[J]. Aerospace Science and Technology, 2016, 51(2): 52-60.

[16] Meng Y, Gao S S, Zhong Y M, et al. Covariance matching based adaptive unscented Kalman filter for direct filtering in INS/GNSS integration[J]. Acta Astronautica, 2016, 120: 171-181.

[17] 赵琳, 王小旭, 孙明, 等. 基于极大后验估计和指数加权的自适应UKF 滤波算法[J]. 自动化学报, 2010, 36(7): 1007-1019.

ZHAO Lin, WANG Xiao-xu, SUN Ming, et al. Adaptive UKF filtering algorithm based on maximum a posterior estimation and exponential weighting[J]. Acta Automatic Sinica, 2010, 36(7): 1007-1019. (in Chinese)

[18] Wu Y X, Hu D W, Wu M P, et al. Unscented Kalman filtering for additive noise case: augmented vs. non-augmented[C]∥Proceedings of the 2005 American Control Conference. Protland, OR, US:IEEE, 2005: 4051-4055.

[19] 田波. 冲击载荷作用下多股簧动态特性试验研究[D]. 重庆大学, 2014: 58-64.

TIAN Bo. Experimental study of dynamic characteristics of stranded wire helical springs under shock load[D]. Chongqing: Chongqing University, 2014: 58-64. (in Chinese)